Journal of Building Construction and Planning Research
Vol.1 No.1(2013), Article ID:29576,7 pages DOI:10.4236/jbcpr.2013.11001
Comparison of School Building Construction Costs Estimation Methods Using Regression Analysis, Neural Network, and Support Vector Machine
![]()
1Department of Plant & Architectural Engineering, Kyonggi University, Suwon-Si, Korea; 2Department of Architectural Engineering, Graduate School of Kyonggi University, Suwon-Si, Korea; 3School of Construction Management and Engineering, University of Reading, Reading, UK.
*Corresponding author: shinys@kyonggi.ac.kr
Received February 16th, 2013; revised March 17th, 2013; accepted March 24th, 2013
Keywords: Estimating Construction Costs; Regression Analysis; Neural Network; Support Vector Machine
ABSTRACT
Accurate cost estimation at the early stage of a construction project is key factor in a project’s success. But it is difficult to quickly and accurately estimate construction costs at the planning stage, when drawings, documentation and the like are still incomplete. As such, various techniques have been applied to accurately estimate construction costs at an early stage, when project information is limited. While the various techniques have their pros and cons, there has been little effort made to determine the best technique in terms of cost estimating performance. The objective of this research is to compare the accuracy of three estimating techniques (regression analysis (RA), neural network (NN), and support vector machine techniques (SVM)) by performing estimations of construction costs. By comparing the accuracy of these techniques using historical cost data, it was found that NN model showed more accurate estimation results than the RA and SVM models. Consequently, it is determined that NN model is most suitable for estimating the cost of school building projects.
1. Introduction
In school building construction projects, budgeting, planning, and monitoring for compliance with the client’s available budget, time, and work outstanding are also important [1]. And the accuracy of construction costs estimation is a key factor in the success of a construction project, and also affects the decision-making by the owners [2-4]. But it is difficult to quickly and accurately estimate the construction costs at the planning stage, because the drawings and documentation are generally incomplete [5]. For this reason, various techniques have been developed to accurately estimate construction costs with the limited project information available in the early stage.
Typical cost estimating techniques are neural networks (NN), support vector machine (SVM), case-based reasoning (CBR), and regression analysis (RA), etc. [6]. For example, the RA model [7-9], NN model [10-13], SVM Model [6,14-16], and CBR model [1,17,18] have been developed for predicting or estimating construction costs. Approaches to cost estimation based on statistics and linear regression analysis have been developed since the 1970s [2]. Since the late 1980s, artificial intelligence approaches such as expert system, NN, and CBR have been applied [19]. In addition, the cost predicting model has been studied since the 2000s.
Previous studies [2,12,20-22] revealed that an NN model for cost estimating is superior to the RA model. Also, the accuracy of cost estimation based on the SVM technique is similar to that of cost estimation based on RA [23]. Consequently, it is necessary to compare RA, NN, and SVM to determine the optimum approach to estimating construction costs.
Therefore, in this research, the accuracy of three estimating techniques (i.e. regression analysis, neural network, and support vector machine techniques) is compared by performing an estimation of construction costs using historical cost data, so that a cost estimation model adapting two techniques (i.e. neural network and support vector machine) could be examined through regression analysis.
2. Three Costs Estimating Techniques
2.1. Regression Analysis
Some studies have mentioned that cost estimating models using regression analysis have several disadvantages: 1) they have no specific, or clearly defined, approach that will help estimators choose the cost model that best fits the historical data to a given cost estimating application [12,20,24,25]; 2) a certain type of multiple equation and its data are assumed to be similar to be suitable for the regression equation [12,24,25]; 3) the variable influencing the estimation must be reviewed in advance, and it is also difficult to use a large number of input variables [24-26]. However, regression analysis, as it is usually called, is a very powerful statistical tool that can be used as both an analytical and predictive technique in examining the contribution of potential new items to the overall estimate reliability [27]. Regression analysis (RA) can be generally represented the form of Equation (1).
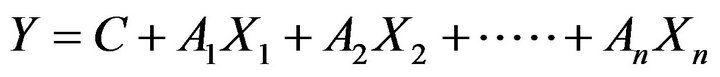 (1)
(1)
where Y is the total estimated costs, and X1, X2,…Xn are measures of distinguishable variables that may help in estimating Y, C is the estimated constant, and A1, A2, …, An are coefficients estimated by regression analysis, given the availability of some relevant data. The Statistical Package for Social Science (SPSS) stepwise techniques were used to develop the regression model.
2.2. Neural Network
A neural network (NN) is a computer system that simulates the learning process of the human brain [2] based on a simplified model of the biological neurons in the human brain and the relations between them. A neural network is modeled in a mathematical manner to implement an intelligent form as shown in the human brain, for utilization in engineering or in other fields [3]. The structure of an NN is as shown in Figure 1. Basically, the network consists of several layers, including an input layer, a hidden layer, and an output layer, and each layer contains neurons. Neurons determine the optimum value through a summation and transfer function. The set of inputs, which is the outputs from another neuron in input layers, are delivered by neurons. Each input data is multiplied by the connection weight, and then the weighted inputs provide output value, which is modified by the transfer function.
Some researchers have explored the application of NN to improve the accuracy of cost estimation beyond that of the regression model [10-12,20,24,25,28,29]. Although many previous studies have proved that the neural network cost estimating model is superior to the regression analysis estimation model, many have also demonstrated not only the superiority of NN but the problems associated with using them for cost estimation [4]. However, the main advantages of an NN are as follows: 1) they can be used to construct high-level nonlinear function esti-
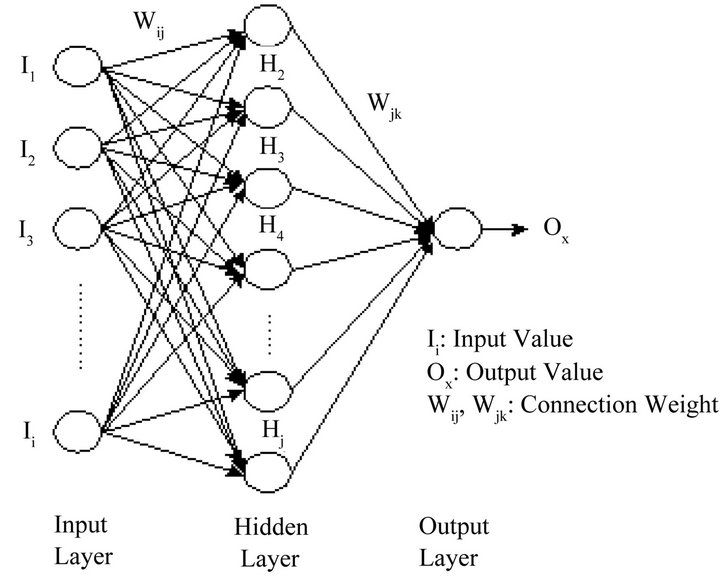
Figure 1. Neural network structure.
mation models; and 2) their use does not impose any limit on the number of features [30]. The main disadvantage of the NN mentioned in the previous research is that the black box techniques and knowledge acquisition process are very time-consuming [11,28,29,31].
2.3. Support Vector Machine
Support vector machine (SVM) is a learning theory developed by Vapnik [32] that has two main categories, support vector classification (SVC) and support vector regression (SVR). In particular, in the model constructed using SVR, the goal is to find a function f(x) that has at most ε deviation from the actually obtained target value (yi) for all the training data, and is simultaneously as flat as possible [33]. The structure of SVR is as shown in Figure 2. The input pattern (support vectors) is mapped into feature space by a map Φ. Then, dot products are computed with the images of the training patterns under the map Φ. This matches up to the evaluating kernel function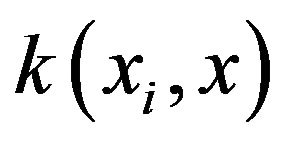 . The dot products are aggregated using the weights
. The dot products are aggregated using the weights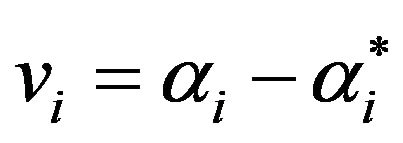 . Last, the final prediction output is calculated by adding the constant value (b).
. Last, the final prediction output is calculated by adding the constant value (b).
In most cases, the performance of SVM generation either matches or is significantly better than that of competing methods such as NN and fuzzy system [34]. However, by comparison with NN, research to apply SVM to cost estimation has not yet been active. Therefore, with only a few studies [6,16,23,35], it is too early to conclude that SVM has superiority in cost estimation. The main advantage of SVM is the capacity for selflearning and high performance in generalization [36]. The main disadvantages of SVM are as follows: 1) it requires a trial and error period to determine both a suitable kernel function and the parameters of the kernel function [16]; 2) SVM models have a high level of algorithmic
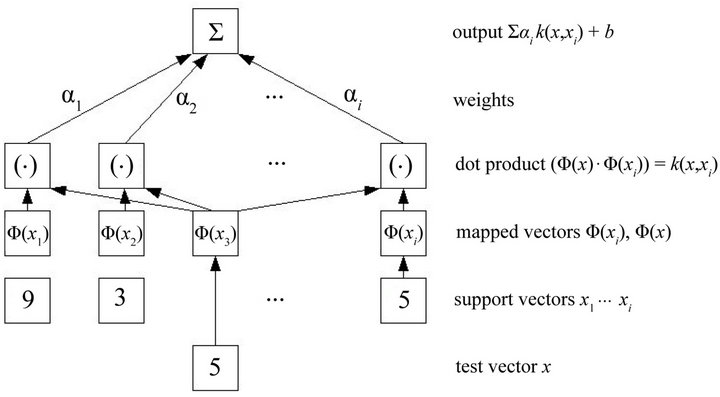
Figure 2. Support vector regression structure.
complexity and require extensive memory [37].
3. Application
3.1. Data for Estimating Construction Costs
The collected data used in this application were the actual construction costs of 217 school building projects executed by general contractors from 2004 to 2007 in Kyeonggi Province, Korea. These cost data were the direct costs of school buildings, such as elementary, middle, and high schools, without mark-up. As shown in Table 1, 10 input and 1 output variables were extracted from the collected data. Notably, the construction year was not used as an input variable because the extracted variables from cost data were converted using the Korean building cost index (BCI), i.e. the collected cost data were multiplied by the BCI of the base year 2005 (BCI = 1.00). The collected cost data of 217 school buildings were divided randomly into 20 test data, 67 cross-validation data, and 130 training data.
3.2. Accuracy Evaluation
Generally, the performance of a cost estimating model is determined by measuring its bias, consistency, and accuracy. Measures of bias, consistency, and accuracy are concerned with the difference in the average between the actual costs and the estimated costs, considering both the degree of variation around the average, and the combination with bias and consistency [2]. By far, the most popular evaluation criteria used involves statistics such as mean, standard deviation, and coefficient of variation [38]. In this research, each model’s performance was measured by the Mean Absolute Error Rates (MAERs), which was calculated by Equation (2).
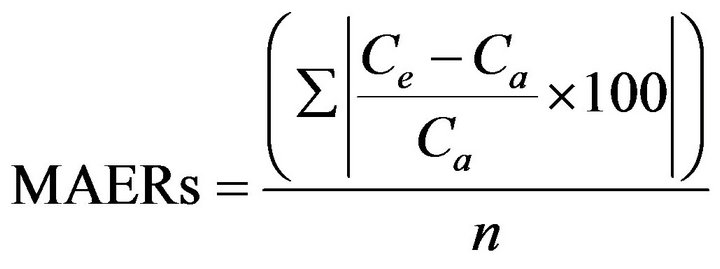 (2)
(2)
where Ce is the estimated construction costs by model application, Ca is the collected actual construction costs,
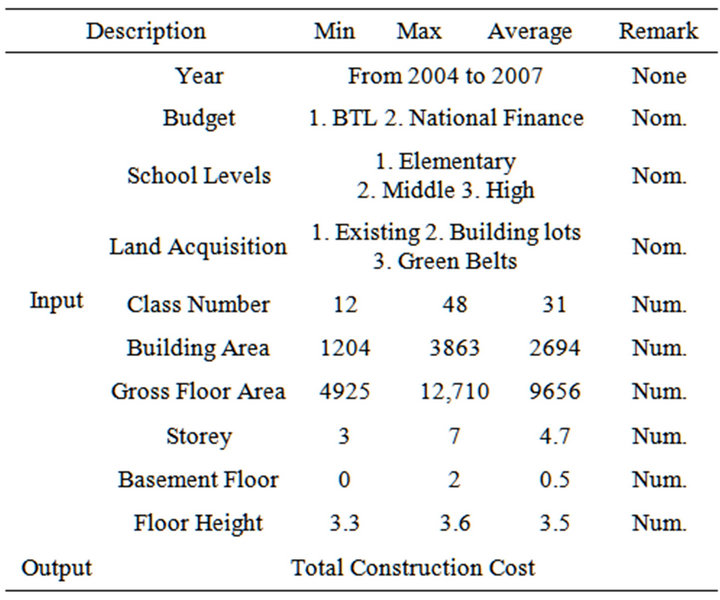
Table 1. Input and output variables.
and n is the number of test data.
3.3. Results of Evaluation
The results from the 20 test data using RA, NN and SVM are summarized in Tables 2 and 3. The results from the RA model had MAERs of 5.68 with 20% of the estimates within 2.5% of the actual error rate, while 80% were within 10%. The NN model had MAERs of 5.27 with 35% of the estimates within 2.5% of the actual error rate, while 85% were within 10%. Last, SVM model had MAERs of 7.48 with 10% of the estimates within 2.5% of the actual error rate, while 75% were within 10%. Also, the standard deviation of the RA, NN, and SVM model are 3.56, 4.13, and 4.66 respectively, as shown in Table 4 and Figure 3.
4. Discussion of Results
This study was conducted by using 217 cases of school building construction projects. Of the cases, 20 cases were used for the testing. The regression model, neural networks model, and support vector machine model with 20 test data gave MAERs of 5.68, 5.27 and 7.48, respectively. Also, the NN model and the RA model had smaller error rates and deviation than that of SVM model. Through the performance, the NN model was the most accurate and reliable of the three models.
The MAERs of three results were then compared using analysis of variance (ANOVA). The MAERs of three results would be statistically similar, even if there were differences between them. The null hypothesis is that MAERs of the three results are all equal (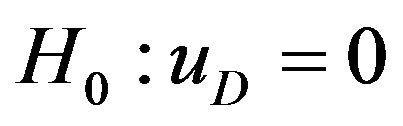 ). The F-statistic is the ratio of the mean squares between the variance of three results. If the F ratio is close to “1”, the null hypothesis is rejected. This analysis showed that
). The F-statistic is the ratio of the mean squares between the variance of three results. If the F ratio is close to “1”, the null hypothesis is rejected. This analysis showed that

Table 2. Summarized results by estimating model.
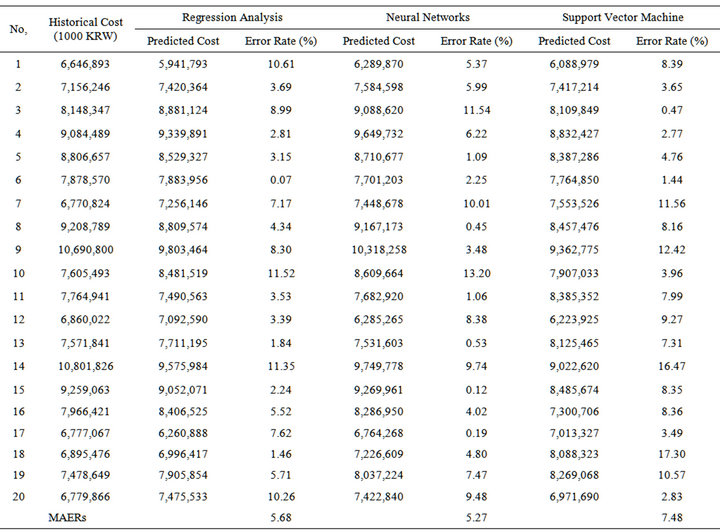
Table 3. Results of estimating costs of each test set.

Table 4. Descriptive analysis of estimating error rate.
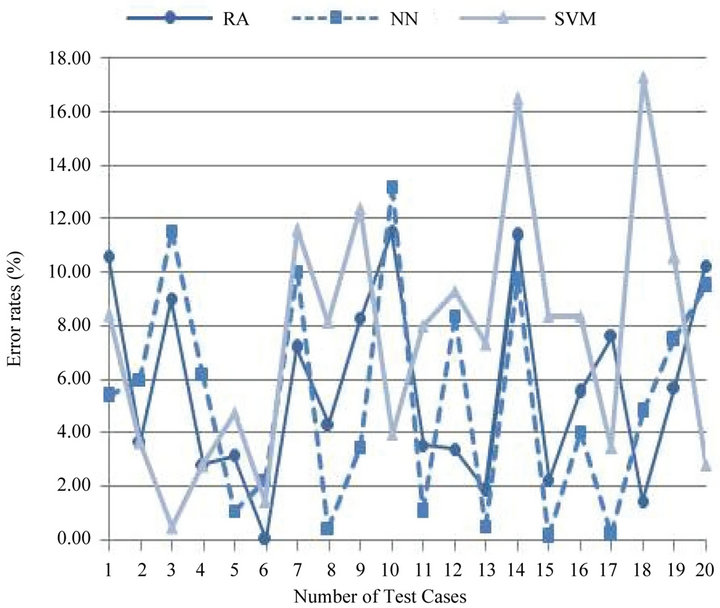
Figure 3. Comparison of the results of each model.
the MAERs of the three results were statistically different. Therefore, the NN model performed more effectively than the other two results in estimating construction costs.
5. Conclusions
This study applied the three techniques of RA, NN, and SVM to estimate the construction cost of school building projects. 197 cases were used for model development and validation, while the remaining 20 cases were used for testing the model. All three models produced a high correlation between the estimating costs and the actual costs.
Although RA, NN, and SVM worked well for the application, NN model gave more accurate estimation results than the RA and SVM models. As mentioned in the previous research, NN has proven to be useful and suitable for dealing with complex problems and developing user-friendly predictive models. They are able to detect any patterns found in the data and provide a greater opportunity to investigate different options and project control techniques. Also, in this study, the NN estimating model is more suitable for estimating school building projects than the SVM estimating model.
REFERENCES
- G.-H. Kim, J.-E. Yoon, S.-H. An, H-H. Cho and K.-I. Kang, “Neural Network Model Incorporating a Genetic Algorithm in Estimating Construction Costs,” Building and Environment, Vol. 39, No. 11, 2004, pp. 1333-1340. doi:10.1016/j.buildenv.2004.03.009
- G.-H. Kim and S.-H. An, “A Study on the Correlation between Selection Methods of Input Variables and Number of Data in Estimating Accuracy; Cost Estimating Using Neural Networks in Apartment Housing Projects,” Journal of the Architectural Institute of Korea, Vol. 23, No. 4, 2007, pp. 129-137.
- G.-H. Kim, S.-H. An and K.-I. Kang, “Comparison of Construction Cost Estimating Models Based on Regression Analysis, Neural Networks, and Case-Based Reasoning,” Building and Environment, Vol. 39, No. 10, 2004, pp. 1235-1242. doi:10.1016/j.buildenv.2004.02.013
- H.-G. Cho, K.-G. Kim, J.-Y. Kim and G.-H. Kim, “A Comparison of Construction Cost Estimation Using Multiple Regression Analysis and Neural Network in Elementary School Project,” Journal of the Korea Institute of Building Construction, Vol. 13, No. 1, 2013, pp. 66-74. doi:10.5345/JKIBC.2013.13.1.066
- S.-H. An and K.-I. Kang, “A Study on Predicting Construction Cost of Apartment Housing Using Experts’ Knowledge at the Early Stage of Projects,” Journal of the Architectural Institute of Korea, Vol. 21, No. 6, 2005, pp. 81-88.
- U.-Y. Park and G.-H. Kim, “A Study on Predicting Construction Cost of Apartment Housing Projects Based on Support Vector Regression at the Early Project Stage,” Journal of the Architectural Institute of Korea, Vol. 23, No. 4, 2007, pp. 165-172.
- S. Singh, “Cost Model for Reinforced Concrete Beam and Slab Structures in Building,” Journal of Construction Engineering and Management, Vol. 116, No. 1, 1990, pp. 54-67. doi:10.1061/(ASCE)0733-9364(1990)116:1(54)
- K.-D. Kim, “A Study on the Development of the Cost Model for the Domestic Apartment House,” Ph.D. Thesis, Seoul National University, Seoul, 1991.
- I.-S. Choi, S.-H. Hong, C.-B. Son and S.-C. Ko, “A Study on the Prediction Model of Construction Cost in HighRise Office Building of SRC Type,” Journal of the Architectural Institute of Korea, Vol. 15, No. 7, 1999, pp. 143-151.
- R. Mckim, “Neural Network Application to Cost Engineering,” Cost Engineering, Vol. 35, No. 7, 1993, pp. 31- 35.
- I.-C. Yeh, “Quantity Estimating of Building with Logarithm-Neuron Networks,” Journal of Construction Engineering and Management, Vol. 124, No. 5, 1998, pp. 374-380. doi:10.1061/(ASCE)0733-9364(1998)124:5(374)
- J. Bode, “Neural Networks for Cost Estimating: Simulation and Pilot Application,” International Journal of Production Research, Vol. 38, No. 6, 2000, pp. 123-154. doi:10.1080/002075400188825
- S.-K. Kim and I.-W. Koo, “A Neural Network Cost Model for Office Buildings,” Journal of the Architectural Institute of Korea, Vol. 16, No. 9, 2000, pp. 59-67.
- X. Wu and L. Cai, “Application of RS-SVM in Construction Project Cost Forecasting,” Proceedings of the 4th International Conference on Wireless Communication, Networking and Mobile Computing, Dalian, 12-14 October 2008, pp. 1-4.
- M.-Y. Cheng and Y.-W. Wu, “Construction Conceptual Cost Estimates Using Support Vector Machine,” Proceedings of the 22nd International Symposium on Automation and Robotics in Construction ISARC 2005, Ferrara, 11-14 September 2005, pp. 1-5.
- S.-H. An, K.-I. Kang, M.-Y. Cho and H.-H. Cho, “Application of Support Vector Machines in Assessing Conceptual Cost Estimates,” Journal of Computing in Civil Engineering, Vol. 21, No. 4, 2007, pp. 259-264. doi:10.1061/(ASCE)0887-3801(2007)21:4(259)
- W. Yunna, “Application of a Case-Based Reasoning Method in Estimating the Power Grid Project Cost,” Proceedings of the 4th International Conference on Wireless Communication, Networking and Mobile Computing, Dalian, 12-14 October 2008, pp. 1-5.
- S.-H. Ji, M. Park and H.-S. Lee, “Case Adaptation Method of Case-Based Reasoning for Construction Cost Estimation in Korea,” Journal of Construction Engineering and Management, Vol. 138, No. 1, 2007, pp. 43-52. doi:10.1061/(ASCE)CO.1943-7862.0000409
- S.-H. An, G.-H. Kim and K.-I. Kang, “A Case-Based Reasoning Cost Estimating Model Using Experience by Analytic Hierarchy Process,” Building and Environment, Vol. 42, No. 7, 2007, pp. 2573-2579. doi:10.1016/j.buildenv.2006.06.007
- J. Garza and K. Rouhana, “Neural Network versus Parameter-Based Application,” Cost Engineering, Vol. 37, No. 2, 1995, pp. 14-18.
- W.-Y. Park, J.-H. Cha and K.-I. Kang, “A Neural Network Cost Model for Apartment Housing Projects in the Initial Stage,” Journal of the Architectural Institute of Korea, Vol. 18, No. 7, 2002, pp. 155-162.
- G.-H. Kim, S.-H. An and H.-K. Cho, “Comparison of the Accuracy between Cost Prediction Models Based on Neural Network and Genetic Algorithm: Focused on Apartment Housing Project Cost,” Journal of the Architectural Institute of Korea, Vol. 23, No. 3, 2006, pp. 111-118.
- J.-M. Shin and G.-H. Kim, “A Study on Predicting Construction Cost of Educational Building Project at Early Stage Using Support Vector Machine Technique,” Journal of Korean Institute of Educational Environment, Vol. 11, No. 3, 2012, pp. 46-54.
- H. Adeli and M. Wu, “Regularization Neural Network for Construction Cost Estimation,” Journal of Construction Engineering and Management, Vol. 124, No. 1, 1998, pp. 18-24. doi:10.1061/(ASCE)0733-9364(1998)124:1(18)
- J. Bode, “Neural Networks for Cost Estimation,” Cost Engineering, Vol. 40, No. 1, 1998, pp. 25-30.
- A. E. Smith and A. K. Mason, “Cost Estimating Predictive Modeling: Regression versus Neural Network,” Engineering Economist, Vol. 42, No. 2, 1997, pp. 137-161. doi:10.1080/00137919708903174
- R. M. Skitmore and B. R. T. Patchell, “Development in Contract Price Forecasting and Bidding Techniques,” In: M. Skitmore and V. Marston, Eds., Cost Modelling, E& FN Spon, London, 1990, pp. 53-84.
- R. Creese and L. Li, “Cost Estimation of Timber Bridge Using Neural Networks,” Cost Engineering, Vol. 37, No. 5, 1995, pp. 17-22.
- H. Li, “Neural Networks for Construction Cost Estimation,” Building Research and Information, Vol. 23, No. 5, 1995, pp. 279-284. doi:10.1080/09613219508727476
- S. Deng and T.-H. Yeh, “Applying Least Squares Support Vector Machines to the Airframe Wing-Box Structural Design Cost Estimation,” Expert Systems with Applications, Vol. 37, No. 12, 2010, pp. 8417-8423. doi:10.1016/j.eswa.2010.05.038
- T. Hegazy, P. Fazio and O. Moselhi, “Developing Practical Neural Network Application Using Back-Propagation,” Computer-Aided Civil and Infrastructure Engineering, Vol. 9, No. 2, 1994, pp. 145-159. doi:10.1111/j.1467-8667.1994.tb00369.x
- V. N. Vapnik, “The Nature of Statistical Learning Theory,” Springer, London, 1999.
- A. J. Smola and B. Schölkopf, “A Tutorial on Support Vector Regression,” Statistics and Computing, Vol. 14, No. 3, 2004, pp. 199-222. doi:10.1023/B:STCO.0000035301.49549.88
- C. J. C. Burges, “A Tutorial on Support Vector Machines for Pattern Recognition,” Data Mining and Knowledge Discovery, Vol. 2, No. 2, 1998, pp. 121-167. doi:10.1023/A:1009715923555
- M.-Y. Cheng, H.-S. Peng, Y.-W. Wu and T.-L. Chen, “Estimate at Completion for Construction Projects Using Evolutionary Support Vector Machine Inference Model,” Automation in Construction, Vol. 19, No. 5, 2010, pp. 619-629. doi:10.1016/j.autcon.2010.02.008
- Y. Shin, D.-W. Kim, J.-Y. Kim, K.-I. Kang, M.-Y. Cho and H.-H. Cho, “Application of Adaboost to the Retaining Wall Method Selection in Construction,” Journal of Computing in Civil Engineering, Vol. 23, No. 3, 2009, pp. 188-192. doi:10.1061/(ASCE)CP.1943-5487.0000001
- P. R. Kumar and V. Ravi, “Bankruptcy Prediction in Banks and Firms via Statistical and Intelligent Techniques—A Review,” European Journal of Operational Research, Vol. 180, No. 1, 2007, pp. 1-28. doi:10.1016/j.ejor.2006.08.043
- M. Skitmore, “Early Stage Construction Price Forecasting: A Review of Performance,” Occasional Paper, Royal Institute of Chartered Surveyors, London, 1991.

