ABSTRACT

Quadratic distance estimation making use of the sample quantile function over a continuous range is introduced. It extends previous methods which are based only on a few sample quantiles and it parallels the continuous GMM method. Asymptotic properties are established for the continuous quadratic distance estimators (CQDE) and the implementation of the methods are discussed. The methods appear to be useful for balancing robustness and efficiency and useful for fitting distribution with model quantile function being simpler than its density function or distribution function.

Keywords:

Covariance Kernel, Influence Function, Hilbert Space, Linear Operator, GMM Estimation, Spectral Decomposition

1. Introduction

For estimation in a classical setup, we often assume to have n independent, identically distributed observations $X_1,\cdots ,X_n$ from a continuous density $f_{{\theta }_0}\left(x\right)$ which belongs to a parametric family $\left\{f_{\theta }\right\}$ , i.e., $f_{{\theta }_0}\left(x\right)\in \left\{f_{\theta }\right\}$ where $\theta ={\left({\theta }_1,\cdots ,{\theta }_m\right)}^{\prime }$ , $\theta \in \Omega$ and ${\theta }_0$ is the true vector of parameters, $\Omega$ is assumed to be compact. One of the main objectives of inferences is to be able to estimate ${\theta }_0$ . In an actuarial context, the sample observations might represent losses of a certain type of contracts and an estimate of ${\theta }_0$ is necessary if we want to make rates or premiums for the type of contract where we have observations.

Maximum likelihood (ML) estimation are density based and often the domain of the density function must not depend on the parameters is one of the regularity conditions so that ML estimators attain the lower bound as given by the information matrix. In many applications, this condition is not met. We can consider the following example which gives the Generalized Pareto distribution (GPD) and draw the attention on the properties of the model quantile function which appears to have nicer properties than the density function and hence motivate us to develop continuous quadratic distance (CQD) estimation using quantiles on a continuum range which generalizes the quadratic distance (QD) methods based on few quantiles as proposed by LaRiccia and Wehrly [1] which can be viewed as based on a discrete range and hence CQD estimation might overcome the arbitrary choice of quantiles of QD as CQD will essentially make use of all the quantiles over the range with $0<p<1$ .

Example (GPD).

The GP family is a two parameters family with the vector of parameter $\theta ={\left(\lambda ,\kappa \right)}^{\prime }$ .

The density, distribution function and quantile function are given respectively by

$f\left(x;\lambda ,\kappa \right)=\frac{1}{\lambda }{\left(1-\frac{\kappa x}{\lambda }\right)}^{\frac{1}{\kappa }-1},1-\frac{\kappa x}{\lambda }\ge 0,\kappa \ne 0,\lambda >0$ and

$f\left(x;\lambda \right)=\frac{1}{\lambda }{\text{e}}^{-x/\lambda },x\ge 0,\kappa =0,\lambda >0$ ,

the distribution function is given by

$F\left(x;\lambda ,\kappa \right)=1-{\left(1-\frac{\kappa x}{\lambda }\right)}^{\frac{1}{\kappa }},1-\frac{\kappa x}{\lambda }\ge 0,\kappa \ne 0,\lambda >0$ and

$F\left(x;\lambda \right)=1-{\text{e}}^{-x/\lambda },x\ge 0,\kappa =0,\lambda >0$ ,

the quantile function is given by

$F^{-1}\left(t;\lambda ,\kappa \right)=\lambda \left(1-{\left(1-t\right)}^k\right)/k,0<t<1,\kappa \ne 0,\lambda >0$ and

$F^{-1}\left(t;\lambda \right)=-\lambda \log \left(1-t\right),\kappa =0,\lambda >0,0<t<1$

These functions can be found in Castillo et al. [2] (pages 65-66). Among these functions only the domain of the quantile function $F^{-1}\left(t;\lambda ,\kappa \right)$ does not depend on the parameters and naturally if the model quantile function satisfies some additional conditions such as differentiability, it is natural to develop statistical inference methods using the sample quantile function $F_n^{-1}\left(t\right)$ instead of the sample distribution function $F_n\left(x\right)$ which are defined respectively as

$F_n^{-1}\left(t\right)=\inf \left\{x|F_n\left(x\right)\ge t\right\}$ and

$F_n\left(x\right)=\frac{1}{n}{\displaystyle {\sum }_{i=1}^n{\delta }_{x_i}}$ with ${\delta }_{x_i}$ being the degenerate distribution at $x_i$ is the commonly used sample distribution. The counterpart of $F_n^{-1}\left(t\right)$ is the model quantile function $F_{\theta }^{-1}\left(t\right)$ , see Serfling [3] (pages 74-80).

Due to the complexity of the density function for the GP model, alternative methods to ML have been developed in the literature for example with the probability weighted moments (PWM) method proposed by Hosking and Wallis [4] which leads to solve moment type of equations to obtain estimators by matching selected empirical moments with their model counterpart. The drawback of the PWM method is the range of the parameters must be restricted for the selected moments to exist, see Hosking and Wallis [4] , Kotz and Nadarajah [5] (p 36). The PWM method might not be robust and some robust methods have been proposed by Dupuis [6] , Juarez and Schucany [7] for estimation for the GP model.

For estimating parameters of the GPD, the percentiles matching (PM) method for fitting loss distributions as described by Klugman et al. [8] (pages 256-257) can also be used. It consists of first selecting two points $t_1,t_2$ , with $0<t_1<t_2<1$ as we only have two parameters and solve the following moment type of estimating equations to obtain the estimators, i.e., ${\widehat{\theta }}_{PM}$ is the vector of solutions of

$F_n^{-1}\left(t_1\right)=F_{\theta }^{-1}\left(t_1\right)$ or equivalently, $F_{\theta }\left(F_n^{-1}\left(t_1\right)\right)=t_1$

and

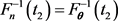or equivalently,.

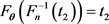The method is robust but not very efficient as only two points are used here to obtain moment type of equations and there is also arbitrariness on the choice of these two points. Castillo and Hadi [9] have improved this method by first selecting a set of two points, 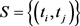and obtain a set of corresponding PM estimators and finally define the final estimators according to a rule to select from the set of PM estimators generated by the set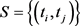. The question on arbitrariness on selecting the set 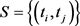is still not resolved with this method.

Instead of solving moment type of equations, for parametric estimation in general not necessary for the GPD with the vector of parameters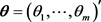, LaRiccia and Wehrly [1] proposed to construct quadratic distance based on the discrepancy of 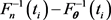using 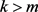selected points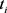’s with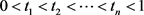, so that we can define the following two vectors 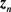and 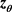with

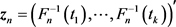
which is based on the sample and its model counterpart defined as

.

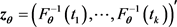This leads to a class of quadratic distance of the form

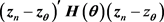(1)

and the quadratic distance (QD) estimators are found by minimizing the objective function given by expression (1), 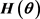is a class of symmetric positive definite matrix which might depend on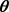. Goodness-of-fit test statistics can also be constructed using expression (1), see Luong and Thompson [10] .

By quadratic distance estimation without further specializing it is continuous we mean that it is based on quadratic form as given by expression (1), it also fits into classical minimum distance (CMD) estimation and closely related to Generalized Methods of moment (GMM) and by GMM without further specializing that it is continuous GMM, we mean GMM based on a finite number of moment conditions, see Newey and McFadden [11] (p 212-2128).

Using the asymptotic theory of QD estimation or CMD estimation, it is well known that by letting 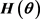to be the inverse of the asymptotic covariance matrix of under, we can obtain estimators which are the most efficient within the class being considered as given by expression (1), so we can let

and

is the asymptotic covariance matrix of.

In fact, it has been shown that it suffices to use a consistent estimate for to obtain asymptotic equivalent estimators. For example, first we obtain a preliminary consistent estimate and if we can construct a consistent estimate

for, i.e.,

then we can construct a consistent estimate which is given for as in general,

.

In practice, for QD estimation we let to obtain QD estimators and the asymptotic efficiency is identical as QD estimators based on and it is simpler to obtain them numerically.

For GMM estimation, it is quite straightforward to construct, see expression (4.2) given by Newey and McFadden [11] (p2155). The authors also pointed out that this might not be the case for CMD estimation or QD estimation. This is a point that we shall address when generalizing the quadratic distance methods using a finite number of quantiles to method using quantile function over a continuous range which we shall refer to as continuous quadratic distances (CQD); we shall use an approach based on the influence functions of the sample quantiles to estimate the optimum kernel which is the analogous of the use of to estimate for the continuous set-up.

Continuous GMM theory makes use of Hilbert space linear operator theory and have been developed in details by Carrasco and Florens [12] and as mentioned it is closely related to the theory for continuous QD, we shall make use of their results to establish consistency and asymptotic normality of continuous quadratic distance estimators and since the paper aims at providing results for practitioners for their applied works, the presentation will emphasize methodologies with less technicalities so that it might be more suitable for applied researchers for their works. First, we shall briefly outline how to form the quadratic distance to obtain the CQD estimators and postpone the details for later sections of the paper.

CQD estimators can be viewed as estimators based on minimizing a continuous quadratic form as given by

(2)

with:

1) is an optimum symmetric positive definite kernel assumed to be fully specified.

2) a and b are chosen values with a being close to 0 and b close to 1 and.

In practice, we work with an asymptotic equivalent objective function instead of where is estimated by a degenerate kernel, i.e.,

. (3)

Since the kernel is degenerate and in our case, we can find explicitly n eigenvalues with corresponding closed form eigenfunctions. These eigenfunctions can be computed explicitly.

As in the spectral decomposition of a symmetric positive defined matrix for the Euclidean space, spectral decomposition in Hilbert space allows the kernel

to be represented as, and using this

representation, we can express as a sum of n components, i.e.,

(4)

which is similar to the expression used to obtain continuous GMM estimators as given by Carrasco and Florens [12] (page 799).

Spectral decompositions in functional space have been used in the literature, see Feuerverger and McDunnough [13] (page 312), Durbin [14] (page 292-294). Furthermore, if are not stable, they can be replaced by suitable defined without affecting the asymptotic theory of the CQD estimators. In practice, we work with

(5)

to obtain CQD estimators. Unless otherwise stated, by CQD estimators we mean estimators using the objective function of the form as defined by expression (5).

Carrasco and Florens [6] (page 799) developed perturbation technique, a technique to obtain from the eigenvalues. The perturbation technique will also be used for constructing a degenerate optimum kernel for CQD estimation.

The objectives of the paper are to develop CQD estimation based on quantiles with the aims to have estimators which are robust in the sense of bounded influence functions and have good efficiencies. For technicalities, we refer to the paper by Carrasco and Florens [12] who have introduced continuous GMM estimation.

The paper is organized as follows. Section 2 gives some preliminary results such as statistical functional and its influence function from which the sample quantiles can be viewed as robust statistics with bounded influence functions. CQD estimation using quantiles will inherit the same robustness property. Some of the standard notions for the study of kernel functions will also be reviewed. By linking a kernel to a linear operator in the Hilbert space of functions which are square integrable over the range with an inner product, it allows a norm to be introduced. Also, the notion of self adjoint linear operator which can be viewed as analogous to a symmetric matrix in Euclidean space is also introduced in Section 2. Section 3 gives asymptotic properties of the CQD estimators based on an estimate optimum kernel. An estimate of the covariance matrix is also given in Section 3.

Finally, we shall mention that simulation studies are not discussed in this paper as numerical quadrature methods are involved for evaluating the integrals over the range for computing the objective function, we prefer to gather numerical aspects and simulation aspects together for further works and include these type of results in a separate paper leaving this paper focusing only on the methodologies.

2. Some Preliminaries

In this section we shall review the notion of statistical functional and its influence function and view a sample quantile as a statistical functional. Using its influence function, we can see that the sample quantile is a robust statistic and using the influence functions of two sample quantiles, we can also obtain the asymptotic covariance of the two sample quantiles.

2.1. Statistical Functional and Its Influence Function

Often, a statistic can be represented as a functional of the sample distribution which we can denote by. For example, the sth-sample quantile is defined as. Associated with, there is its influence function which is a weak functional directional derivative at in the direction of, is the degenerate distribution at x. More specifically, the influence function of as a function of x is defined as

,

is a linear function in the functional space. It is not difficult to see that we can also compute using the usual derivative

.

Furthermore, since a Taylor type of approximation in a functional space can be used, we then have the following approximation expressed with a remainder term

or equivalently using,

and using is linear,

,

.

If as a function of x is bounded, the statistics is robust and the remainder is with being a term which converges to 0 in probability faster than as.

Therefore, if we want to find the asymptotic variance of , it is given by the variance of as

The influence function of the sth-sample quantile can be obtained and it is given by

(6)

from which we can obtain the asymptotic variance of

,

See Serfing [3] (page236), Hogg et al. [15] (page 593). Also, using the influence function representation for the sth-sample quantile and the corresponding one for the tth-sample quantile, it can be shown that the asymptotic covariance of the following sample quantiles and is given by

see LaRiccia and Wehrly [1] (page 743).

If we define the covariance kernel as

(7)

then associated to this kernel there is a linear operator in a functional space which can be defined as follows, let a function which belongs to the functional space being considered, K is defined as

.

We can see that for a suitable functional space, it is natural to consider the Hilbert space of functions which are square integrable so that a norm and linear operators can be defined in this space. This will facilitate the studies of kernels which are function of. The necessary notions are introduced in the following section.

2.2. Linear Operators Associated with Kernels in a Hilbert Space

The functional space that we are interested is the space of integrable function with the range and it is natural to introduce an inner product and therefore, a norm can be defined as

.

For a Euclidean space, the composition of two linear operators and where and are matrices produces a matrix with. For linear operators in the Hilbert space the composition of the linear operators and is a linear operator with its kernel and

.

Just as a matrix has its transpose matrix and if is symmetric then, these notions can be extended to a functional space as a linear operator has its adjoint and if the kernel defining is symmetric then, is called self adjoint.

More precisely, given is found using the following equality, see Definition 6 given by Carrasco and Florens [12] (page 823),

Furthermore,

if then.

In this paper we focus on positive definite symmetric kernel which can be viewed as the covariance of for some stochastic process; therefore, the objective function is of the type is always positive unless then, see Luenberger [16] (page 152) for this notion.

Unless otherwise stated, we work with linear operators associated with positive definite symmetric kernels. For the Euclidean space if the covariance matrix is invertible with the inverse given by assumed to exist after regularizations then there are symmetric positive definite symmetric matrices denoted by and so that

(8)

see Hogg et al. [15] (pages 179-180) for square root of a symmetric positive definite matrices and they can be computed using the technique of spectral decomposition of matrices.

If is linear operator with covariance kernel, the analogous properties given by expression (8) continues to hold but unlike matrices where closed forms for the matrices can be found, one might not be able to display the kernel of or explicitly as no closed form expressions are available despite that both and exist subject to some technical regularizations as discussed in section 4 by Carrasco and Florens [12] (pages 506-510).

For our purpose, we shall focus on a linear operator with its kernel defined by Equation (7) for the rest of the paper. Since and are related and if we can construct an estimator for, we can construct an estimator for and the construction of these estimators will be discussed in the next sub-section.

2.3. Estimation of K and K⁻¹

The methods used to construct an estimator for follows from the techniques proposed by Carrasco and Florens [12] . The steps are given below:

1) We need a preliminary consistent estimate for, for our case we can minimize the following simple objective function to obtain,

.

2) Use and the sample of observations to construct a degenerate kernel which has the form

, and depends on.

For our set-up, i.e., CQD estimation, we should use the influence function of the sample quantiles as given by expression (6) to specify,.

The notion of influence function was not mentioned in Carrasco and Florens [12] .

3) Since is a degenerate kernel it only has n eigenvalues with the corresponding eigenvectors, these eigenvectors have closed forms. The procedures to find these eigenvalues and eigenvectors have been given Carrasco and Florens [12] (page 805) and will be summarized in the next paragraphs. Let be one of these n eigenvalues with its corresponding eigenvector, needs to satisfy

, i.e.,.

4) Use the spectral decomposition to express using its eigenvalues and eigenfunctions, i.e.,

.

The above expression is similar to the representation of a positive definite matrix using the spectral decomposition and from which we only need to adjust the eigenvalues if we want to find, the inverse of the matrix or the matrices and.

We can proceed as follows in order to find and , following Carraco and Florens [12] (page 805). First we form a matrix with

.

It turns out that for each j is also an eigenvalue of the matrix and its eigenvectors is with respect to the matrix with

and.

The eigenfunction can be expressed as and they

can be computed as statistical packages often offer routines to compute eigenvalues and eigenvectors for a given matrix.

For numerical evaluations of a numerical quadrature procedure is needed to compute the integrals over a range.

Now we turn into attention of constructing and to estimate and.

It appears then the kernel of can be defined as

, see Definition 3 given by Carrasco and Florens [12] (page 807). Howewer, Carrasco and Florens [12] (page 799) have shown that will create numerical instabilities and need to be regularized and instead of, we need to replace it by, and since are positive in probability, we can also let and these expressions might be easier to handle numerically.

Now we can define define to be the kernel of, will be a valid estimator for providing that the sequence and using their Theorem 7 on page 810.

For example, if we let for some d chosen to be positive then the requirements for the sequence are met.

This also means that the kernel for can be defined as

(9)

and again is a valid estimator for.

This also means that and can be replaced by and whenever they appear in expressions or equations used to derive asymptotic properties for the CQD estimators based on their Theorem 7.

In Section 3 we shall turn our attention to asymptotic properties of CQD estimators using the objective function an using the norm, it can also be expressed neatly as

with and

is the linear operator as defined by expression (9).

For consistency, we shall make use the basic consistency Theorem, i.e., Theorem 2.1 as given by Newey and McFadden [12] (page 2121). For establishing asymptotic normality for the CQD estimators, the procedures are similar to those used for establishing asymptotic normality of continuous GMM estimators as given by Theorem 8 given by Carrasco and Florens [12] (page 811, page 825).

3. Asymptotic Properties

3.1. Consistency

Assuming and is compact and observe that

. (10)

Now if we assume that the integrand can be dominated by a function which does not depend and furthermore then we have uniform convergence in probability, i.e., uniformly with

,

is the optimum symmetric positive definite kernel of. Therefore, is uniquely minimized at, this implies consistency of the CQD estimators given by the vector using the basic consistency Theorem. Therefore, , the symbol denotes convergence in probability. We implicitly assume that the conditions and are met.

3.2. Asymptotic Normality

The basic assumption used to establish asymptotic normality for the CQD estimators is the model quantile function is twice differentiable which allows a standard Taylor expansion the estimating equations.

Assuming the first derivative vector and the second derivative matrix

exist.

Before considering the Taylor expansion, we also need the following notation and the notion of a random element with zero mean and covariance given by the kernel of the associated linear operator K, i.e., , see Remark 2 as given by Carrasco and Florens [12] (page 803). Note that if we let, using the Mean value Theorem, we then have

,

lies in the segment joining and. Now we have which satisfies which is also given by

(11)

as is symmetric. Using inner product and Hilbert space as in the proofs of Theorem 2 by Carrasco and Florens [12] (page 825), expression (11) can be expressed as

. (12)

Using expression (12), we then have

.

Now using is a linear operator, , rearranging the terms gives the following equality in distribution

.

Note that and the symbol denotes equality in distribution.

Let

And then it is easy to see that

,

so that

(13)

with the symbol denotes convergence in law or in distribution.

The matrix plays the same role as the information matrix for maximum likelihood (ML) estimation. Clearly, needs to be estimated, an estimate is given as

, (14)

using the spectral decomposition technique, the element of can be expressed as

(15)

4. Summary and Conclusion

The proposed method is similar to the continuous GMM method with the estimators obtained using sample distribution function obtained by minimizing

with

being an optimum kernel but using a sample distribution function instead of the sample quantile function as studied by Carrasco and Florens [12] (page 816) for nonnegative continuous distributions. The kernel is constructed with the use of, being the usual indicator function.

The authors also showed that by letting, the continuous GMM estimators are as efficient as ML estimators.

For robustness sake for continuous GMM estimation we might want to let 𝑇 be finite and the lower bound be so that the optimum kernel remains bounded for the regions of the double integrals used to define the continuous GMM objective function. This can be viewed as equivalent to choose and for the integrals of the objective function for CQD estimation. For robustness sake, it appears simpler to work with the domain (a, b) instead of as numerical quadrature methods applied over the range (a, b) might be simpler to implement. We conjecture that CQD estimators can also be fully efficient just as the continuous GMM estimators as defined above despite a proof is still lacking for the time being by letting,. More numerical and more simulation studies are needed but we hope that based on the presentation of this paper the proposed method is implementable and its asymptotic properties useful so that applied researchers might want to consider to use them for their works especially for fitting models where the model quantile function is simpler to handle than its model distribution or density function and especially when there is a need for robust estimation with the data.

Acknowledgements

The helpful and constructive comments of a referee which lead to an improvement of the presentation of the paper and support from the editorial staffs of Open Journal of Statistics to process the paper are all gratefully acknowledged.

Conflicts of Interest

The author declares no conflicts of interest regarding the publication of this paper.

Cite this paper

Luong, A. (2019) Robust Continuous Quadratic Distance Estimation Using Quantiles for Fitting Continuous Distributions. Open Journal of Statistics, 9, 421-435. https://doi.org/10.4236/ojs.2019.94028

References