Received 12 April 2016; accepted 5 June 2016; published 8 June 2016

ABSTRACT

For multi-way tables with ordered categories, the present paper gives a decomposition of the point-symmetry model into the ordinal quasi point-symmetry and equality of point-symmetric marginal moments. The ordinal quasi point-symmetry model indicates asymmetry for cell probabilities with respect to the center point in the table.

Keywords:

Decomposition, Multi-Way Table, Ordinal Quasi Point-Symmetry, Point-Symmetry

1. Introduction

Consider an 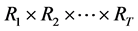table with ordered categories. Let 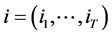for 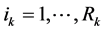and 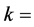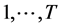, and let 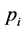denote the probability that an observation will fall in ith cell of the table. Let 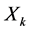denote the kth variable of the table for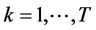. Denote the hth-order (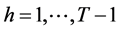) marginal probability

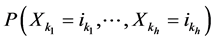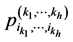by with.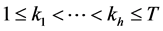

In the case of 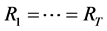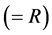, the symmetry (S^T) model is defined by

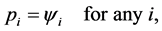
where for any permutation of i (Bhapkar and Darroch, [1] ; Agresti, [2] , p. 439). We may also refer to this model as the permutation-symmetry model.

The hth-order marginal symmetry () model is defined by, for a fixed h (),

where is any permutation of, and for any and (Bhapkar and Darroch, [1] ). The hth-order quasi symmetry () model is defined by, for a fixed h (),

where for any permutation j of i (Bhapkar and Darroch, [1] ). Bhapkar and Darroch [1] gave the theorem that:

1) For the table and a fixed h (), the S^T model holds if and only if both the and models hold.

Tahata, Yamamoto and Tomizawa [3] considered the hth-linear ordinal quasi symmetry () model, which was defined by, for a fixed h (),

where for any permutation j of i. This model is a special case of the model. The model is the ordinal quasi symmetry model when (Agresti, [4] , p. 244). Tahata et al. [3] also considered the hth-order marginal moment equality () model, which was expressed as, for a fixed h (),

where for. Tahata et al. [3] obtained the theorem that:

2) For the table and a fixed h (), the S^T model holds if and only if both the and models hold.

Various decompositions of the symmetry model are given by several statisticians, e.g. Caussinus [5] , Bishop, Fienberg and Holland ( [6] , Ch.8), Read [7] , Kateri and Papaioannou [8] , and Tahata and Tomizawa [9] .

For the table, the point-symmetry (P^T) model is defined by

where and with for (Wall and Lienert, [10] ; Tomizawa, [11] ). This model indicates the point-symmetry of cell probabilities with respect to the center point of multi-way table.

For the table, Tahata and Tomizawa [12] considered the hth-order marginal point-symmetry () model defined by, for a fixed h (),

Tahata and Tomizawa [12] also considered the hth-order quasi point-symmetry () model defined by, for a fixed h (),

where. Tahata and Tomizawa [12] gave the theorem that:

3) For the table and a fixed h (), the P^T model holds if and only if both the and models hold.

Theorem 3) is Theorem 1) with structures in terms of permutation-symmetry, i.e. the S^T, and models, replaced by structures in terms of point-symmetry, i.e. the P^T, and models. However, a theorem in terms of point-symmetry corresponding to Theorem 2) is not obtained yet. So we are now interested in the decomposition of the P^T model.

In the present paper, Section 2 proposes three models. Section 3 gives a new decomposition of the P^T model. Section 4 provides the concluding remarks.

2. Models

Let, where denotes the largest integer less than or equal to x.

Consider the model defined by, for a fixed odd number h (),

where

and for. We shall refer to this model as the hth-order marginal moment point-symmetry () model. Note that if the model holds then the model holds. Under the model, we see, for any k (),

Then we obtain, for any and (),

Under the model, we see, for any, and (),

Then we obtain, for any, , and (),

Thus we are not interested in the model with h being even. Therefore we shall consider the model with h being odd.

Consider the model defined by

where. We shall refer to this model as the ordinal quasi point-symmetry (OQP^T) model. In the case of, this model is identical to the model proposed by Tahata and Tomizawa [13] . The special case of the OQP^T model obtained by putting is the P^T model. Also the OQP^T model is the special case of the model obtained by putting. The OQP^T model may be expressed as

with and. From this equation, we can see the log-odds that an ob- servation falls in ith cell instead of in the point-symmetric i^*th cell, i.e., is described as a linear combination with intercept and slope for the category indicator under the OQP^T model. Thus the parameter can be interpreted as the effect of a unit increase in the kth variable on the log-odds.

Consider the model being more general than the OQP^T model as follows, for a fixed odd number h (),

where. We shall refer to this model as the hth-linear ordinal quasi point-symmetry () model. Especially, when, the model is identical to the OQP^T model. Also the model is the special case of the model obtained by putting, and

.

Figure 1 shows the relationships among models.

3. Decomposition of Point-Symmetry

We obtain the following theorem:

Theorem 1. For the table and a fixed odd number h (), the P^T model holds if and only if both the and models hold.

Proof. If the P^T model holds, then both the and models hold. Assuming that both the and models hold, then we shall show the P^T model holds. Let denote cell pro- babilities which satisfy both the and models. The model is expressed as

where. Let

Note that satisfy, and. Then the model is also ex-pressed as

(1)

The model is expressed as

(2)

where

Then we denote () by.

Consider arbitrary cell probabilities which satisfy the model and

(3)

where

From (1), (2) and (3),

(4)

Let denote the Kullback-Leibler information, e.g., it between q and is

From (4),

Thus, for fixed,

and then q uniquely minimize (see Darroch and Ratcliff, [14] ).

Let. Then, in a similar way as described above, we obtain

and then uniquely minimize, hence. Namely q satisfy the P^T model. The proof is completed.

For the analysis of data, the test of goodness-of-fit of the model is achieved based on, e.g., the likelihood ratio chi-square statistic which has a chi-square distribution with the number of degrees of freedom

Also the number of degrees of freedom for the model is

We point out that, for a fixed h, the number of degrees of freedom for the P^T model is equal to sum of those for the and models.

4. Concluding Remarks

For multi-way contingency tables, we have proposed the, OQP^T and models. Under the OQP^T model, the log-odds that an observation falls in a cell instead of in its point-symmetric cell is described as a linear combination of category indicators. For a fixed odd number h (), the model implies the model.

We have gave the theorem that the P^T model holds if and only if both the and models. For the analysis of data, the decomposition given in the present paper may be useful for determining the reason when the P^T model fits data poorly.

Acknowledgements

The authors thank the editor and the referees for their helpful comments.

Cite this paper

Yusuke Saigusa,Kouji Tahata,Sadao Tomizawa, (2016) Decomposition of Point-Symmetry Using Ordinal Quasi Point-Symmetry for Ordinal Multi-Way Tables. Open Journal of Statistics,06,381-386. doi: 10.4236/ojs.2016.63033

References