Open Journal of Statistics
Vol.05 No.05(2015), Article ID:58220,4 pages
10.4236/ojs.2015.55037
Selecting a Component with Longer Mean Life Time in Bivariate Pareto Models
Parameshwar V. Pandit, Shubhashree Joshi
Department of Statistics, Bangalore University, Bangalore, India
Email: panditpv12@gmail.com, shubhashreejoshi13@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 10 June 2015; accepted 20 July 2015; published 23 July 2015
ABSTRACT
In any parallel system, selecting a component with longer mean lifetime is of interest to the researchers. Hanagal (1997) [1] discussed selection procedures for a two-component system with bivariate exponential (BVE) models. In this paper, the problem of selecting a better component with reference to its mean life time under bivariate Pareto (BVP) models is considered. Three selection procedures based on sample proportions, sample means and maximum likelihood estimators (MLE) are proposed. The probability of correct selection for the proposed procedures is evaluated through Monte Carlo simulation using normal approximation. The asymptotic relative efficiency (ARE) of the proposed procedures is presented to facilitate the evaluation of the performance of procedures.
Keywords:
Asymptotic Relative Efficiency (ARE), Better Component, Bivariate Pareto, Probability of Correct Selection

1. Introduction
The problem of determining the component with longer life time in a two-component parallel system when the two components are dependent is of interest in the present context. The component which has longer mean life time is considered to be a better component. Hanagal [1] considered selecting the better component in a parallel system with two dependent components when the joint distribution life time of the components is bivariate exponential (BVE) distribution. Hanagal [1] considered BVE distribution proposed by Freund [2] , Marshall-Olkin [3] and Block-Basu [4] . Hyakuntake [5] considered the above problem when (X1, X2) follows BVE distribution of Marshall-Olkin. However selection of the better component when (X1, X2) follows other than BVE has not been considered in the literature.
The main aim of this paper is to select a best component with reference its life length in a two component parallel system developing a proper statistical tool. Here, the components of the system are assumed to be dependent and their lifetimes follow bivariate Pareto distribution.
The problem of selecting the component in a two dependent component parallel system when life times (X1,X2) of two components follow bivariate Pareto (BVP) distribution is considered in this paper. Three selection procedures are proposed and their probabilities of correct selection are evaluated.
2. Selection Procedures
Veenus and Nair [6] proposed BVP model with survival function
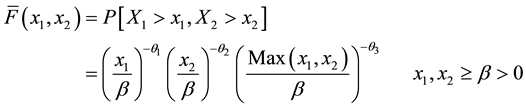 (1)
(1)
where 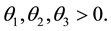 In this paper, assume β = 1, we get the survival function of (X1, X2) given by
In this paper, assume β = 1, we get the survival function of (X1, X2) given by
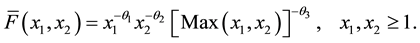 (2)
(2)
The pdf of (X1, X2) is given by

where 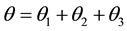
The above BVP model is not absolutely continuous with respect to Lebesgue measure on  and has a posi-
and has a posi-
tive probability on the diagonal i.e.,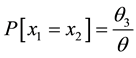 . The random variables X1 and X2 are independent iff
. The random variables X1 and X2 are independent iff
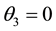 and X1 and X2 have identical marginal’s iff
and X1 and X2 have identical marginal’s iff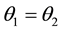 .
.
Let 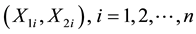 be a random sample of size n from BVP and let n1(n2) be the number of obser-
be a random sample of size n from BVP and let n1(n2) be the number of obser-
vations with X1 < X2 (X1 > X2) in the sample of size n. The distribution of (n1, n2) is trinomial 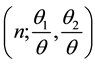
where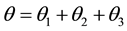 .
.
We propose three selection procedures:
The first selection procedure R1 is based on counts
R1: Select C1 as better component if n2 > n1 and select C2 when n2 < n1.
The second selection procedure is based on the sample means of two lifetimes of the components
R2: Select C1 as better component if 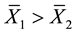 and select C2 as better component when
and select C2 as better component when 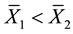
where 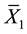 and
and 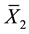 are the sample means of the lifetimes of the two components C1 and C2 respectively.
are the sample means of the lifetimes of the two components C1 and C2 respectively.
The third selection procedure R3 is based on MLE’s
R3: Select C1 as better component if 



By the assumption θ1 < θ2 (selecting the component C1) the probability of correct selection based on three procedures are
The exact distribution of





where

where



Hence


tion of standard normal distribution,

3. Determination of Minimum Sample Size and Asymptotic Relative Efficiency (ARE)
The probability requirement based on the selection procedure Ri, i = 1, 2, 3 is 

That is, 



The minimum sample size required for the selection procedure Ri is
The ARE of the selection procedure Ri with respect to the selection procedure Rj is given by

The AREs are presented in Table 1 for some combinations of (θ1, θ2, θ3)
Table 1 gives the efficiency of three procedures R1, R2 and R3. The efficiency comparison would be useful in choosing an appropriate procedure.
4. Some Remarks and Conclusions
1) It is observed from the table that the selection procedure R2 based on sample means performs better than the other two selection procedures R1 and R3.
Table 1. The AREs for some combinations of (θ1, θ2, θ3).
2) The selection procedures R1 and R3 are equally efficient.
3) The probability of correct selection under selection procedures is computed when the sample size is large and the result is similar to that obtained through AREs.
4) The problem of selecting the best component in multi components parallel system is under progress for multivariate exponential (MVE) and multivariate Pareto (MVP) distributions.
Cite this paper
Parameshwar V.Pandit,ShubhashreeJoshi, (2015) Selecting a Component with Longer Mean Life Time in Bivariate Pareto Models. Open Journal of Statistics,05,355-359. doi: 10.4236/ojs.2015.55037
References
- 1. Hanagal, D.D. (1997) Selection of a Better Component in Bivariate Exponential Models. Journal of the Italian Statistical Association, 5, 453-460.
- 2. Freund, J.E. (1961) A Bivariate Extension of the Exponential Distribution. Journal of the American Statistical Association, 56, 971-977.
http://dx.doi.org/10.1080/01621459.1961.10482138 - 3. Marshall, A.W. and Olkin, I. (1967) A Multivariate Exponential Distribution. Journal of the American Statistical Association, 62, 30-44.
http://dx.doi.org/10.1080/01621459.1967.10482885 - 4. Block, H.W. and Basu, A.P. (1974) A Continuous Bivariate Exponential Extension. Journal of the American Statistical Association, 69, 1031-1037.
- 5. Hyakuntake, H. (1992) Selecting the Better Component of a Bivariate Exponential Distribution. Statistics and Decisions, 10, 153-162.
- 6. Veenus, P and Nair, K.R.M. (1994) Characterization of a Bivariate Pareto Distribution. Journal of the Indian Statistical Association, 32, 15-20.
- 7. Hanagal, D.D. (1997) Note on Estimation of Reliability under Bivariate Pareto Stress-Strength Model. Statistical Papers, 38, 453-459.
http://dx.doi.org/10.1007/BF02926000
Appendix
Maximum Likelihood Estimators of the parameters (θ1, θ2, θ3) of BVP distribution
The likelihood of the sample of size n is
where n1 be the number of observations with X1i < X2i in the sample of size n and
The log likelihood of (X1i, X2i) 
The likelihood equations are
Maximum Likelihood Estimators are obtained solving above likelihood equations simultaneously. One can generate some consistent estimators say 



So we choose some consistent estimators as follows
where
Hence it is easy to check that 
Thus 
trix 

















