Open Journal of Statistics
Vol.05 No.02(2015), Article ID:55567,6 pages
10.4236/ojs.2015.52012
Estimation of the Population Mean Using Paired Ranked Set Sampling
B. S. Biradar1, C. D. Santosha2
1Department of Studies in Statistics, University of Mysore, Mysore, India
2All India Institute of Speech and Hearing, Mysore, India
Email: biradarbs@statistics.uni-mysore.ac.in, getsanthoshcd@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 24 February 2015; accepted 1 April 2015; published 13 April 2015
ABSTRACT
In the situation where the sampling units in a study can be easily ranked than quantified, the ranked set sampling methods are found to be more efficient and cost effective as compared to SRS. In this paper we propose an estimator of the population mean using paired ranked set sampling (RSS) method. The proposed estimator is an unbiased estimator of the population mean when the set size is even. In case of odd set size the estimator is unbiased when the underlying distribution is symmetric. It is shown that the proposed estimator is more efficient than its counterpart SRS method for all distributions considered in this study.
Keywords:
Ranked Set Sampling, Paired Ranked Set Sampling, Population Mean, Relative Efficiency, Errors in Ranking

1. Introduction
Ranked set sampling (RSS) enables one to provide more structure for the collected sample items, and use this structure to develop efficient inferential procedures. This approach to data collection was first proposed by McIntyre ([1] , reprinted in [2] ) for situations where taking the actual measurements for sample observations was difficult (maybe costly, destructive, time-consuming), but mechanisms for either informally or formally ranking a set of sample units was relatively easy and reliable. In RSS one first draws m2 units at random from the population and partitions them into m sets of m units. The m units in each set are ranked without making actual measurements. From the first set of m units the unit ranked lowest is chosen for actual quantification. From the second set of m units the unit ranked second lowest is measured. This process is continued until the unit ranked largest is measured from the m-th set of m units. If a larger sample size is required then the procedure can be repeated r times to obtain a sample of size n = rm. These chosen elements are called a ranked set sample.
Dell and Clutter [3] and Takahasi and Wakimoto [4] provided mathematical foundations for RSS. Dell and Clutter [3] also showed that the estimator for population mean based on RSS is at least as efficient as the estimator based on SRS with the same number of measurements even when there were ranking errors. Samawi et al. [5] used extreme ranked set sample (ERSS) in case of even sample size which is easier to use than the usual RSS procedure to estimate the population mean. Muttlak [6] proposed the use of median ranked set sampling (MRSS) method for estimating the population mean. Muttlak [7] investigated quartile ranked set sampling (QRSS) for estimating the population mean. Jemain et al. [8] suggested balanced groups ranked set sampling (BGRSS) for estimating population mean. Biradar and Santosha [9] studied the use of extremes RSS for estimating population mean. Recent summaries of RSS literature appear in two survey articles by Wolfe [10] [11] and a monograph by Chen et al. [12] . These procedures are based on quantification of single unit from each sample. However, more than one order statistics from each sample contain additional information about the unknown parameter. Therefore it is sensible to have more than one quantified observations (order statistics) from each sample to construct an estimator or test of a hypothesis. Recently, Balci et al. [13] introduced two modified RSS by choosing two elements from each sample. They have studied modified maximum likelihood estimator (MMLE) and best linear unbiased estimator (BLUE) when the underlying distribution is normal. The main objective of this paper is to propose a nonparametric estimator using these paired RSS and to compare with estimators based on SRS and extremes RSS (RSS (E)) recently studied by Biradar and Santosha [9] under both perfect and imperfect ranking (with errors in ranking).
2. Ranked Set Sampling by Choosing Diagonals of Samples (RSS (D))
Balci et al. [13] introduced modified RSS by choosing paired units from each sample and they have called this sampling scheme as RSS (D).
The procedure of RSS (D) is described as follows:
1) Select m simple random samples each of size m.
2) Each sample is ranked in itself as in ranked set sampling design.
3) Then the i-th smallest and (m + i − 1)-th largest order statistics from i-th sample for 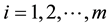 are measured.
are measured.
4) Repeat above steps r times until the desired sample size n = 2rm is obtained.
We assume that the i-th lowest and (m + i − 1)-th largest units of this set can be detected visually, or by any other means easily.
Let  be a random sample of size 2m with probability density function f(x) with a finite mean
be a random sample of size 2m with probability density function f(x) with a finite mean 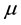 and variance
and variance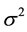 . Let
. Let 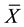 be the mean of the SRS of size 2m. The mean and variance of
be the mean of the SRS of size 2m. The mean and variance of  are known to be
are known to be 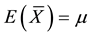 and
and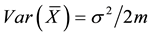 , respectively. Let
, respectively. Let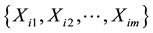 ,
, 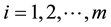 be m sets of independent random samples each of size m from a population with distribution function F(x) and probability density function f(x) with mean
be m sets of independent random samples each of size m from a population with distribution function F(x) and probability density function f(x) with mean  and variance
and variance . Let
. Let 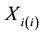 and
and  denote the i-th and (m + 1 − i)-th order statistics of the i-th sample respectively,
denote the i-th and (m + 1 − i)-th order statistics of the i-th sample respectively,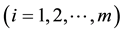 . Then
. Then
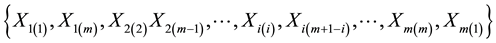
is a RSS (D) of size 2m. Note that the order statistics within the sample are dependent and between the samples are independent. For all





The estimator of the population mean based on RSS (D) can be defined in case of even sample size m as

The mean and variance of 
and

In case of an odd sample size m, the estimator of the population mean can be defined as

And it follows that

If the underlying distribution is symmetric about zero, then 

[14] have shown that 


Using the above results for odd sample size 

3. Efficiency
The efficiency of 

Similarly, we compare the proposed estimator 

Then
is a RSS (E) of size 2m. For all






where 

Note that if the underlying distribution is symmetric about its mean then 
The variance of the of 

The efficiency of 

The relative efficiencies were computed for m = 2(2)10 and are presented in Table 1. Considering the results in Table 1, a gain in efficiency is obtained by using RSS (D) for different values of m and for all the distributions considered in this study. The estimator 


Table 1. The variances and relative efficiencies of estimators of population mean using RSS (E), RSS (D), SRS.
4. Paired Ranked Set Sampling with Errors in Ranking
Dell and Clutter [3] considered the case in which there were errors in ranking; that is the quantified observation from the i-th sample may not be the i-th order statistic rather the i-th judgement order statistic. They showed that sample mean of RSS with errors in ranking was an unbiased estimator of the population mean regardless of the errors in ranking, and has smaller variance than the usual estimator based on SRS with same sample size. But the variance of the estimator with errors in ranking will be larger than the variance of the estimator with perfect ranking and less than or equal to the variance of the estimator based on SRS.
Let 


denote RSS (D) sample with errors in ranking. The estimators of the population mean using RSS (D) with errors in ranking is defined as


with variance

and

To gain some insight of the effect of ranking errors on the efficiencies of the estimators various simulation trails were conducted. We use the simulation method considered by Dell and Clutter [3] and David and Lavine [15] . In the first stage we generate m sets of simple random samples




where 





Now the RSS (D) and RSS (E) procedures were used to get the values of the estimators for population mean. Based on 10,000 simulated samples estimates of means and varainces or mean squared error (MSE) of estimators were computed. These trails were run with standard deviation set at 0.05, 0.25, 0.5 and 0.75. The results are presented in Table 2 and Table 3.
The efficieny values in Table 2 suggest that for all the cases (for allvalues of m and distributions considered here) RSS (D) estimator is more efficient than the SRS estimator in the presence of erros in ranking. Table 2 also shows that efficiency values increase with m and decrease with errors in ranking. This indicates that lesser the extent of errors in ranking better the performance of RSS (D) estimator.
Table 2. The relative efficiencies of estimators of population mean based on RSS (D) w.r.t. SRS.
Table 3. The relative efficiencies of estimators of population mean based on RSS (D) w.r.t. RSS (E).
From Table 3 we can observe that except for uniform distribution RSS (D) estimator performs better than RSS(E) estimator in the presence of errors in ranking. In the case of exponential, normal and logistic distri- butions the efficency values increase with m and decrease with errors in ranking. For uniform distribution the opposite trend can be observed, i.e., efficency values increase with 
References
- McIntyre, G.A. (1952) A Method for Unbiased Selective Sampling Using Ranked Sets. Australian Journal of Agricultural Research, 3,385-390. http://dx.doi.org/10.1071/AR9520385
- McIntyre, G.A. (2005) A Method for Unbiased Selective Sampling, Using Ranked Sets. The American Statistician, 59, 230-232. Originally Appeared in Australian Journal of Agricultural Research, 3, 385-390. http://dx.doi.org/10.1198/000313005X54180 http://dx.doi.org/10.1071/AR9520385
- Dell, T.R. and Clutter, J.L. (1972) Ranked Set Sampling Theory with Order Statistics Background. Biometrics, 28, 545-555. http://dx.doi.org/10.2307/2556166
- Takahasi, K. and Wakimoto, K. (1968) On Unbiased Estimates of the Population Mean Based on the Sample Stratified by Means of Ordering. Annals of the Institute of Statistical Mathematics, 20, 1-31. http://dx.doi.org/10.1007/BF02911622
- Samwi, H., Ahmad, M. and Abu-Dayyeh, W. (1996) Estimating the Population Mean Using Extreme Ranked Set Sampling. Biometrical Journal, 38, 577-586. http://dx.doi.org/10.1002/bimj.4710380506
- Muttlak, H.A. (1997) Median Ranked Set Sampling. Journal of Applied Statistical Sciences, 6, 245-255.
- Muttlak, H.A. (2003) Investigating the Use of Quartile Ranked Set Samples for Estimating the Population Mean. Journal of Applied Mathematics and Computation, 146, 437-443. http://dx.doi.org/10.1016/S0096-3003(02)00595-7
- Jemain, A.A., Al-Omari, A. and Ibrahim, K. (2008) Some Variations of Ranked Set Sampling. Electronic Journal of Applied Statistical Analysis, 1, 1-15.
- Biradar, B.S. and Santosha, C.D. (2015) Estimation of the Population Mean Based on Extrmemes Ranked Set Sampling. American Journal of Mathematics and Statistics, 5, 32-36.
- Wolfe, D.A. (2004) Ranked Set Sampling: An Approach to More Efficient Data Collection. Statistical Science, 19, 636-643. http://dx.doi.org/10.1214/088342304000000369
- Wolfe, D.A. (2010) Ranked Set Sampling. Wiley Interdisciplinary Reviews: Computational Statistics, 2, 460-466. http://dx.doi.org/10.1002/wics.92
- Chen, Z.H., Bai, Z.D. and Sinha, B.K. (2004) Ranked Set Sampling: Theory and Applications. Springer, New York. http://dx.doi.org/10.1007/978-0-387-21664-5
- Balci, S., Akkaya, A.D. and Ulgen, B.E. (2013) Modified Maximum Likelihood Estimators Using Ranked Set Sampling. Journal of Computational and Applied Mathematics, 238,171-179. http://dx.doi.org/10.1016/j.cam.2012.08.030
- Arnold, B.C., Balkrishna, N. and Nagaraj, H.N. (1992) A First Course in Order Statistics. John Wiley and Sons, New York.
- David, H.A. and Levine, D.N. (1972) Ranked Set Sampling in the Presence of Judgment Ranking Error. Biometrics, 28, 553-555.










