Received 28 December 2014; accepted 16 January 2015; published 20 January 2015

ABSTRACT

Extending the work carried out by [1] , this paper proposes six combined-type estimators of population ratio of two variables in post-stratified sampling scheme, using variable transformation. Properties of the proposed estimators were obtained up to first order approximations, 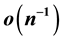, both for achieved sample configurations (conditional argument) and over repeated samples of fixed size n (unconditional argument). Efficiency conditions were obtained. Under these conditions the proposed combined-type estimators would perform better than the associated customary combined-type estimator. Furthermore, optimum estimators among the proposed combined- type estimators were obtained both under the conditional and unconditional arguments. An empirical work confirmed the theoretical results.

Keywords:

Variable Transformation, Combined-Type Estimator, Ratio, Product and Regression-Type Estimators, Mean Squared Error

1. Introduction

The use of information on auxiliary character to improve estimates of population parameters of the study variable is a common practice in sample survey, and sometimes, information on several variables is used to estimate or predict a characteristic of interest. The investigators often collect observations from more than one variable, including the variable of interest 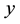and some auxiliary variables. The use of these variables (known as auxiliary information in sample survey design) often results in efficient estimate of population parameters (e.g. mean, ratio, proportion, etc.) under some realistic conditions, especially when there is a strong correlation between the study variables and the auxiliary variables. Many authors have made contributions in this regard, including [2] and [3] . In this context, ratio, product and regression methods of estimation are good examples. Ratio and product-type estimators take advantage of the correlation between the auxiliary variable and the study variable, to improve the estimate of the characteristic of interest. For example, when information is available on the auxiliary variable that is highly positively correlated with the study variable, the ratio method of estimation proposed by [4] is a suitable estimator to estimate the population mean, and when the correlation is negative, the product method of estimation, as envisaged by [5] and [6] , is appropriate. However, in some studies, the ratio of the population means (or totals) of the study and auxiliary variables might be of great significance, hence the need to estimate such ratios.

The customary estimator of the population ratio 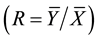of the population means of two variables, and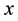, under the simple random sampling scheme, is given as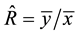, which is the ratio of the sample means of the two variables ( [2] and [7] ). The estimator, 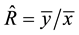, uses information on only two variables, namely the study variable 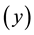and one auxiliary variable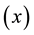. However, several authors, like [7] and [8] , have contributed to the problem of estimating the population ratio of two means, often utilizing additional information on one or more auxiliary variables, say. While it is possible to record increased efficiency by introducing such additional auxiliary variables, it is obvious that extra cost is involved in order to obtain information on such additional auxiliary variables. References [1] and [9] have argued that such extra cost could be avoided by using variable transformation of the already observed auxiliary variable, instead of introducing additional (new) auxiliary variables. However, the works carried out by [1] [9] were restricted to estimation of population ratio in simple random sampling scheme. The present study is necessitated by the need to extend to post- stratified sampling scheme, the works on ratio estimation carried out by [1] [9] under the simple random sampling scheme. This is in order to extend to other sampling schemes, the obvious advantage of reduced cost in the use of variable transformation instead of introducing additional (new) auxiliary variables when estimating population ratio of two population parameters.

2. The Proposed Combined-Type Estimators

Let 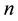units be drawn from a population of 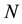units using simple random sampling method and let the sampled units be allocated to their respective strata, where is the number of units that fall into stratum such

that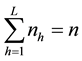. Let and be the observation on the study and auxiliary variables, respectively.

Consider the following variable transformation of the auxiliary variable, , under post-stratified sampling scheme.

(2.1)

An equivalent of the transformation (2.1), in simple random sampling scheme, has been used by authors like [1] [8] - [13] . The associated sample mean estimator of the transformed variable (2.1), in post-stratified sampling scheme, can be written as

(2.2)

and and are sample mean estimators based on and respectively. Using

the sample means, and, and assuming that the population mean, of the auxiliary variable, is known, we proposed six combined-type estimators of the population ratio in post stratified sampling scheme as

(2.3)

(2.4)

(2.5)

(2.6)

(2.7)

(2.8)

2.1. Conditional Properties of the Proposed Estimators

Reference [14] defined that under the conditional argument, that is, for the achieved sample configuration, the post stratified estimator, is unbiased for the population mean, , with variance

(2.9)

where refers to conditional variance and is the population variance of in stratum. Similarly, Onyeka (2012) obtained the conditional variance of and the conditional covariance of and respectively as:

(2.10)

and

(2.11)

where is the population variance of in stratum, is the covariance of and in stratum, and refers to conditional covariance.

Let

(2.12)

Then, under the conditional argument,

(2.13)

(2.14)

(2.15)

(2.16)

Using (2.12), the first proposed estimator, , given in (2.3), can be re-written up to first order approximation, , in expected value, as

(2.17)

and

(2.18)

We take conditional expectation of (2.17) and (2.18), and use (2.13) to (2.16) to make the necessary substitutions. This gives the conditional bias and mean square error of respectively as

(2.19)

and

(2.20)

where

(2.21)

Following similar procedure, we obtain the conditional biases and mean square errors of the six proposed estimators, together with those of the customary combined-type estimator, , of population ratio, in post-stratified sampling, up to first order approximation, , as:

(2.22)

(2.23)

(2.24)

(2.25)

(2.26)

(2.27)

(2.28)

and

(2.29)

(2.30)

(2.31)

(2.32)

(2.33)

(2.34)

(2.35)

Generally, we have for the proposed six combined-type estimators,

(2.36)

where and

(2.37)

2.2. Unconditional Properties of the Proposed Estimators

Following [14] we obtain the following (unconditional) variances and covariance, for repeated samples of fixed size n.

(2.38)

(2.39)

and

(2.40)

where is the population sampling fraction. By taking unconditional expectations of (2.17) and (2.18), and using (2.38)-(2.40) to make the necessary substitutions, we obtain the unconditional bias and mean square errors of the first proposed estimator, , up to first order approximation, , as:

(2.41)

and

(2.42)

where

(2.43)

Following similar procedure, we obtain the unconditional biases and mean square errors of the six proposed estimators, together with those of the customary combined-type estimator, , of population ratio, in post-stratified sampling, up to first order approximation, , as:

(2.44)

(2.45)

(2.46)

(2.47)

(2.48)

(2.49)

(2.50)

and,

(2.51)

(2.52)

(2.53)

(2.54)

(2.55)

(2.56)

(2.57)

Generally, the unconditional mean square errors of the proposed combined-type estimators is obtained as

(2.58)

where, is as given in (2.37).

3. Efficiency Comparison

The efficiencies of the six proposed combined-type estimators are first compared with that of the customary combined ratio estimator in estimating the population ratio of two population means under the conditional and unconditional arguments in post-stratified random sampling scheme. Secondly, the performances of the proposed estimators among themselves are investigated. Furthermore, the optimum estimators among the proposed estimators are also obtained. The efficiency comparison is carried out using the mean square errors of the estimators and the results are shown in Table 1.

4. Numerical Illustration

Here, we use the final year GPA and the level of absenteeism of 2012/2013 graduating students of Statistics Department, Federal University of Technology Owerri to illustrate the properties of the estimators proposed in the present study. Absenteeism is measured as the average number of days absent from lectures in a month. The class consists of 50 students, with 32 and 18 students respectively falling into low-absenteeism (0 - 3 days per month) and high-absenteeism (4 - 6 days per month) groups or strata. Our interest is to estimate the ratio of final year GPA to absenteeism from lectures, based on a post-stratified sample of 20 out of the 50 graduating students in the class. The data statistics, consisting mainly of population parameters are shown in Table 2.

Table 3 shows the percentage relative efficiencies (PRE-1) of the proposed combined-type estimators, ,

Where, and, is as given in (2.37).

over the customary combined-type estimator, , under the conditional and under the unconditional arguments. The table also shows the percentage relative efficiency (PRE-2) of the proposed combined-type estimators, , over the other combined-type estimators, under the conditional and under the unconditional arguments.

Table 3 shows that apart from the estimators, and, the remaining four proposed combined-type estimators, under the conditional and under the unconditional arguments, are more efficient than the customary combined-type estimator, , for the data under consideration, and their gains in efficiency (PRE-1) are relatively large. Also, using PRE-2, we observe that the proposed combined-type estimator, , is more efficient than the estimators, , , and, under the conditional and unconditional arguments. The optimum estimator, as expected, has the highest gain in efficiency, both under the conditional and unconditional arguments. However, the customary combined-type estimator, on the other hand, is found to be more efficient than some of the proposed combined-type estimators for the given set of data. This confirms the theoretical results, which showed that the proposed estimators are not always more efficient than the customary combined-type estimator. Notice that and showing that and from the theoretical results in Table 1, the proposed estimators would be more efficient than the customary combined-type estimator, under the unconditional argument, if. The empirical results in Table 3 show that and, and the proposed estimators (PRE-1 = 44%) and (PRE-1 = 65%) under the unconditional argument, are less efficient than the customary combined-type estimator,. Hence the empirical results confirm the theoretical results.

5. Concluding Remarks

The study extends use of variable transformation in estimating population ratio in simple random sampling scheme to post-stratified sampling scheme. Efficiency conditions for preferring the proposed estimators to the customary combined-type estimator are obtained. The study shows that in any given survey, these efficiency conditions should be employed in order to determine the appropriate proposed combined-type estimators to use for the purpose of estimating the population ratio of two variables in post-stratified sampling scheme, using variable transformation.

References