Abstract

Normally the mass of a root has a uniform distribution but some have different uniform distributions named Generalized Uniform Distribution (GUD). The characterization result based on expectation of function of random variable has been obtained for generalized uniform distribution. Applications are given for illustrative purpose including a special case of uniform distribution.

Keywords: Characterization, Generalized Uniform Distribution (GUD)

1. Introduction

Normally the mass of a root has a uniform distribution. Plant develops into the reproductive phase of growth; a mat of smaller roots grows near the surface to a depth of approximately 1/6-th of maximum depth achieve (see G. Ooms and K. L. Moore [1] ). Dixit [2] studied the problem of efficient estimation of parameters of a uniform distribution in the presence of outliers. He assumed that a set of random variables 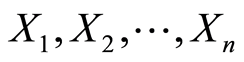represents the masses of roots where out of n-random variables some of these roots (say k) have different masses; therefore, those masses have different uniform distributions with unknown parameters and these k observations are distributed with Generalize Uniform Distribution (GUD) with probability density function (pdf)

(1.1)

where are known constants; is positive absolutely continuous function and is everywhere differentiable function. Since derivative of being positive, range is truncated by from right.

Dixt [3] obtained Maximum Likelihood Estimator (MLE) and the Uniformly Minimum Variance (UMVU) estimator of reliability functional, 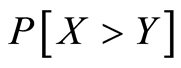in the same setup and showed that the UMVUE is better than MLE when one parameter of GUD is known, where as both parameters of the GUD are unknown, is estimated by using mixture estimate and is consistent.

In this paper the problem of characterization of GUD with pdf given in (1.1) has been studied and the characterization also holds for uniform distribution on interval when. Various approaches were used to characterize uniform distribution; few of them have used coefficient of correlation of smaller and the larger of a random sample of size two; Bartoszyn’ski [4] , Terreel [5] , Lopez-Bldzquez [6] as Kent [7] , have used independence of sample mean and variance; Lin [8] , Too [9] , Arnold [10] , Driscoll [11] , Shimizu [12] , and Abdelhamid [13] have used moment conditions, n-fold convolution modulo one and inequalities of Chernoff-type were also used (see Chow [14] and Sumrita [15] ).

In contrast to all above brief research background and application of characterization of member of Pearson family, this research does not provide unified approach to characterized generalized uniform.

The aim of the present research note is to give a path breaking new characterization for generalized uniform distribution through expectation of function of random variable, using identity and equality of expectation of function of random variable. Characterization theorem was derived in Section 2 with method for characterization as remark and Section 3 devoted to applications for illustrative purpose including special case of uniform distribution.

2. Characterization

Theorem 2.1. Let be a continuous random variable (rv) with distribution function 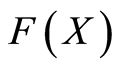having pdf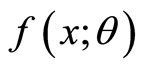. Assume that is continuous on the interval, where. Let 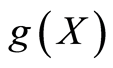be a differentiable functions of on the interval, where 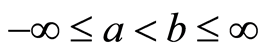and more over 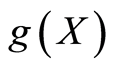be nonconstant. Then 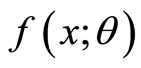is the pdf of Generalize Uniform Distribution (GUD) defined in (1.1) if and only if

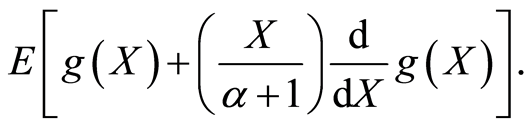(2.1)

Proof: Given defined in (1.1), if is such that where 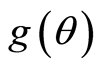is differentiable function then

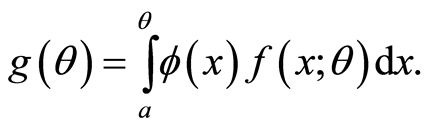(2.2)

Differentiating with respect to on both sides of (2.2) and replacing X for after simplification one gets

(2.3)

which establishes necessity of (2.1). Conversely given (2.1), let be the pdf of rv X such that

(2.4)

Since, the following identity holds

(2.5)

Differentiating with respect to x and simplifying after tacking 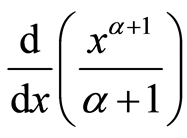as one factor one gets (2.5) as

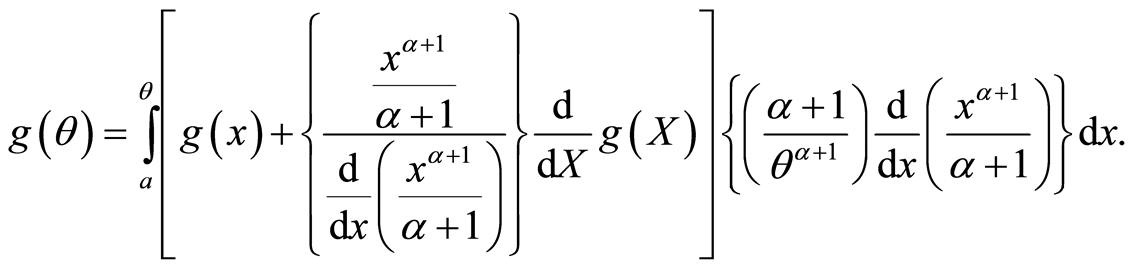(2.6)

Substituting derivative of in (2.6) it reduces to

(2.7)

where is derived in (2.3) and by uniqueness theorem from (2.4) and (2.7)

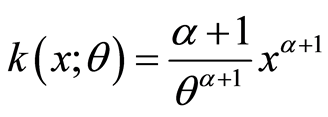(2.8)

Since is decreasing function for 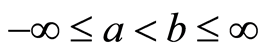and is satisfy only when range of X is truncated by from right and integrating (2.8) on the interval on both sides, one gets 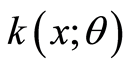derived in (2.8) as

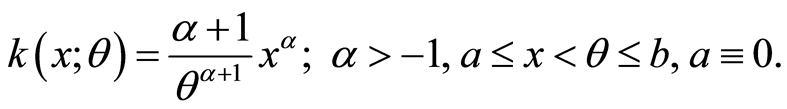(2.9)

and

Hence 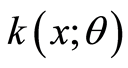derived in (2.9) reduces to 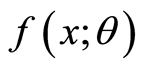defined in (1.1) which establishes sufficiency of (2.1).

Remark 2.1. Using derived in (2.3), the given in (1.1) can be determined by

(2.10)

and pdf is given by

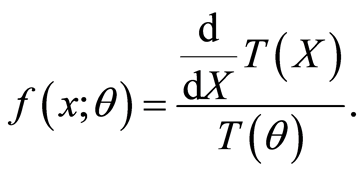(2.11)

where 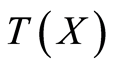is increasing function for 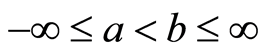with 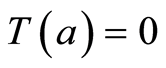such that it satisfies

(2.12)

Remark 2.2. If characterization theorem 2.1 also holds for uniform distribution with pdf

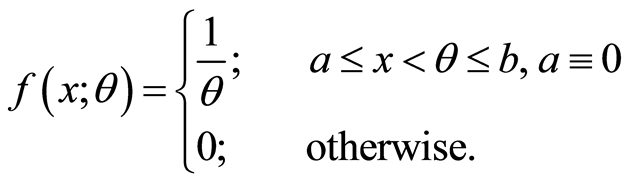(2.13)

3. Examples

Using method describe in remark 2.1 Generalize Uniform Distribution (GUD) through expectation of non-constant function of random variable such as mean, raw moment, , , 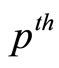quantile, distribution function, reliability function and hazard function is given to illustrate application and significant of unified approach of characterization result (2.1) of theorem 2.1.

Example 3.1. Characterization of Generalize Uniform Distribution (GUD) through hazard function

therefore

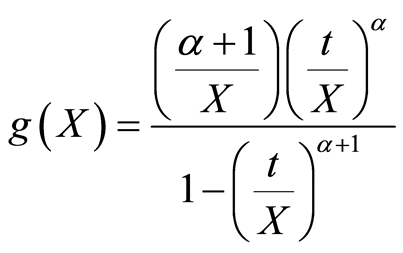From (2.3) one get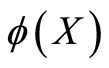s as

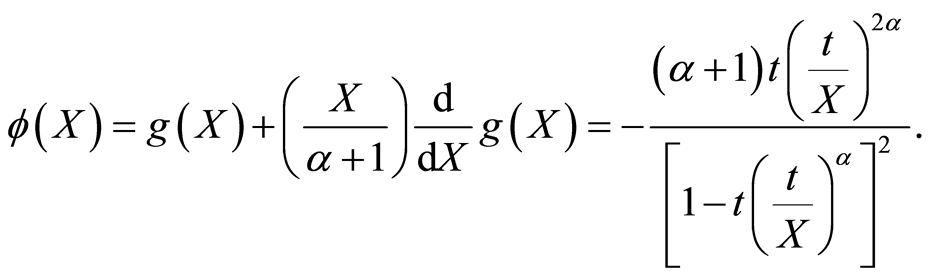
and using (2.10) of remark 2.1 the

By characterization method describe in remark 2.1, if

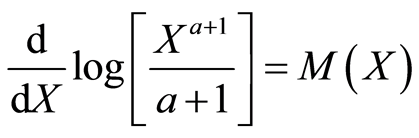
then

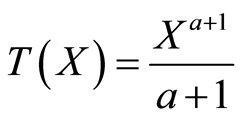
and substituting 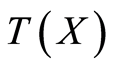as appeared in (2.12) for (2.11),

is characterized.

Example 3.2. The characterization of 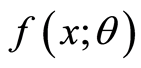defined in (2.1) through non constant function such as

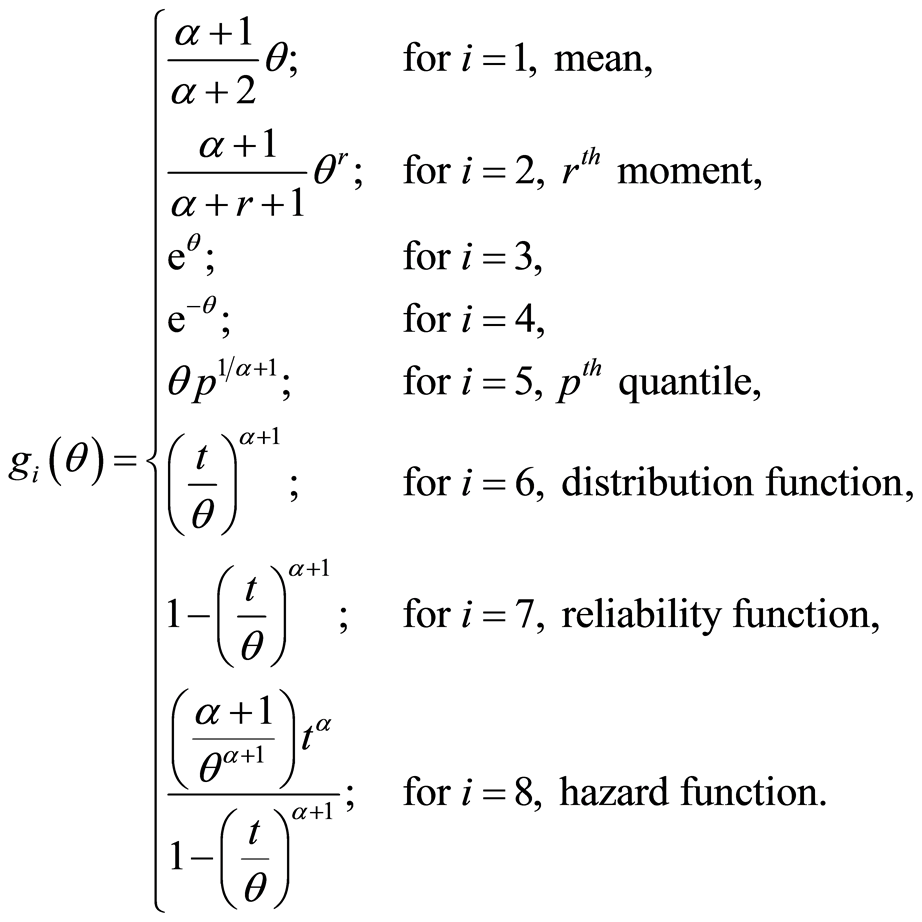(3.1)

and using

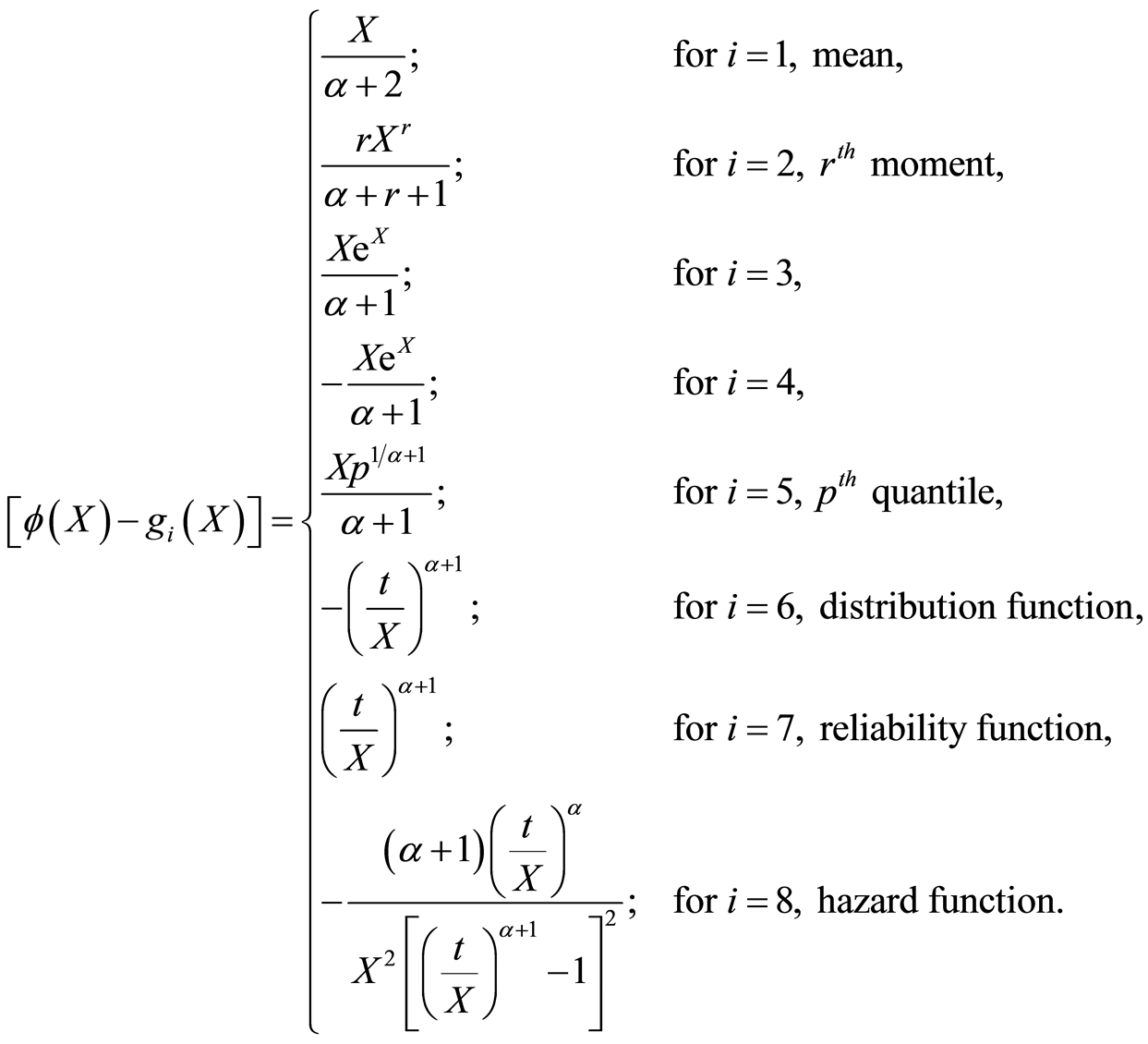(3.2)

and defining given in (2.10) and substituting as appeared in (2.12) for (2.11), is characterized.

Example 3.3. In context of remark 2.2 uniform distribution with pdf given in (2.13) characterized through quantile

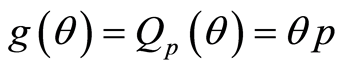
therefore

.

From (2.3) one gets as

and using (2.10) of remark 2.1 the

.

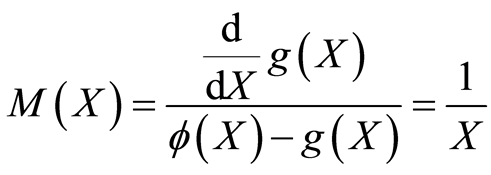By characterization method describe in remark 2.1, if

then

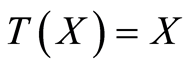
Example 3.3. The pdf 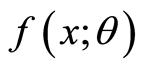defined in (2.13) can be characterized through non-constant function such as

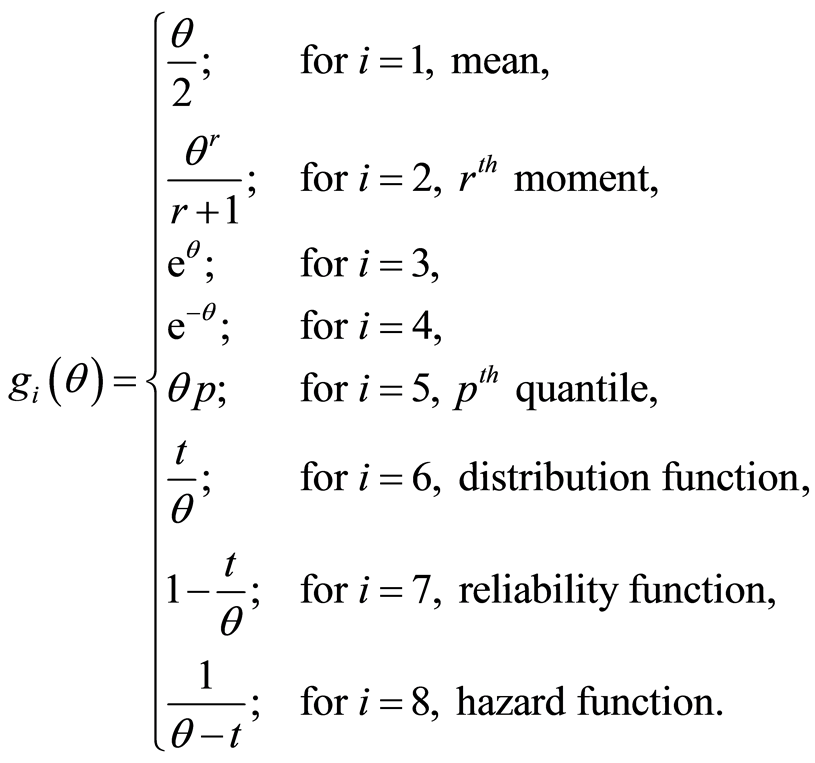
and using

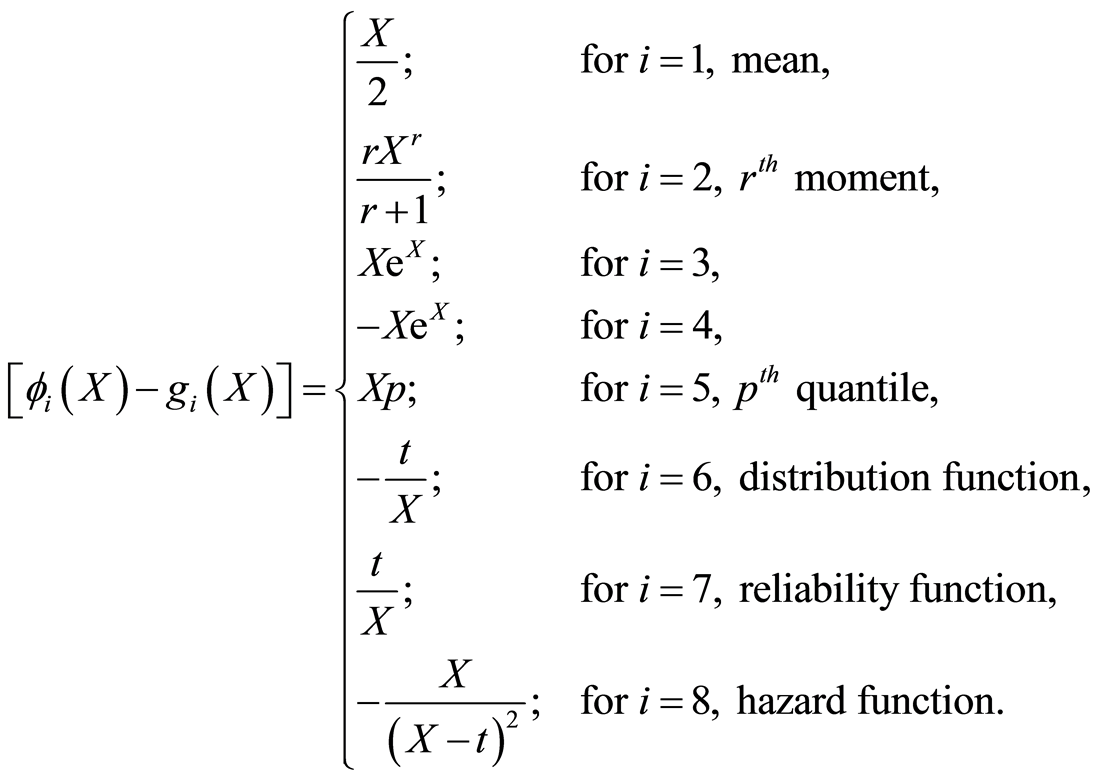
and defining given in (2.10) and substituting as appeared in (2.12) for (2.11), is characterized.

4. Conclusion

To characterize pdf defined in (1.1) one needs any arbitrary non-constant function of X which should be differentiable and integrable only.

Acknowledgements

This work is supported by UGC Major Research Project No: F.No.42-39/2013 (SR), dated 12-3-2013.

References