Open Journal of Statistics
Vol.04 No.02(2014), Article ID:43277,6 pages
10.4236/ojs.2014.42011
Acute-to-Chronic Ratio as a Metric for HIV Surveillance
Zonghui Hu, Dean A. Follmann
Biostatistics Research Branch, National Institute of Allergy and Infectious Diseases, National Institutes of Health, Bethesda, USA
Email: huzo@niaid.nih.gov, dfollmann@niaid.nih.gov
Copyright © 2014 Zonghui Hu, Dean A. Follmann. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Zonghui Hu, Dean A. Follmann. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
ABSTRACT
Received October 23, 2013; revised November 23, 2013; accepted November 30, 2013
Early diagnosis is important for HIV control on both the individual and the population level. Patients who are diagnosed shortly after infection have more treatment options which can result in delayed progression to AIDS. Early diagnosis can also help to reduce the spread of HIV: with viral loads at the highest level, the newly infected have the highest risk of transmitting HIV to partners. Accordingly it is important to evaluate at a population level whether individuals are diagnosed shortly after infection. For this purpose, we introduce the acute-to- chronic ratio, which is the odds of the infected individuals being diagnosed in the acute infection stage versus the chronic infection stage among those who seek HIV testing. We demonstrate this new metric through HIV testing results from sexually transmitted disease clinics of four cities, and compare the four populations with respect to how quickly the infected get HIV testing.
Keywords:
Acute Infection; Chronic Infection; HIV; Maximum Likelihood
1. Introduction
We introduce a new metric in this article for evaluating the rapidity with which the infected seek HIV testing. It is a potentially useful measure to compare the effectiveness of HIV surveillance across different populations as well as monitoring a population over the time.
People go through different stages upon HIV infection. Immediately after infection, no antibodies are produced by the human immune system and the HIV viruses replicate very quickly. Characteristic of this initial stage is a high HIV viral load and no detectable antibody level. We refer to this early stage as the acute or acute infection [1]. After acute infection, antibodies are produced which, along with other processes, cause the viral load to drop to a lower and more stable level. Characteristic of this later stage is detectable HIV-specific antibodies. We refer to this late stage as the chronic infection. In HIV screening, standard tests such as the rapid HIV test (OraQuick) look for antibodies and can detect only the chronic infection. For acute infection, HIV RNA based tests such as PCR (Polymerase Chain Reaction) and NAAT (nucleic acid amplification test) are used which can detect the actual HIV viruses.
Detection of early HIV infection has been named as a priority [2]. Diagnosis of acute infections―in the antibody negative “window period”―is particularly important. Individuals diagnosed at the acute infection stage have more treatment options for reducing viral loads and enhancing HIV-specific immune response, and consequently have a better chance of delaying progression to AIDS. For public health, since the acutely infected have the maximal transmission potential due to the high viral loads [3], effective early diagnosis can help reduce the spread of HIV by allowing critical prevention services at the acute infection stage [4]. Consequently, early diagnosis is an important aspect for HIV control.
As the antibody-negative window is relatively short, about 3 weeks [5], diagnosis of acute infection requires HIV testing shortly after infection. For a population at a given time, those going for HIV testing fall into three categories: the acutely infected, the chronically affected, and the uninfected. As diagnosis of acute infection requires HIV testing within the antibody negative window, a low proportion of acute infection can be due to a low proportion of infection or delayed testing beyond the window. We propose a new metric as the ratio of the proportion of acute infection versus that of chronic infection. It measures the odds of the infected being diagnosed during acute versus chronic stage. The new metric reflects the rapidity of the infected subjects seeking and obtaining HIV testing. All things being equal, that is, the population of those who seek testing is stable over the time or locations, a high acute infection to chronic ratio is desirable.
We illustrate the new metric with data from sexually transmitted (STD) clinics in Malawi, North Carolina [6], San Francisco [7], and Washington DC [8], which were collected around the years 2000 to 2003. Table 1 lists the number of subjects going for HIV testing, the number of diagnosed acute infections, and the number of diagnosed chronic infections. Also the listed are the per capita incomes around the time of data collection. We are interested in whether the four regions share the same acute-to-chronic ratio; that is, whether the infected individuals in these regions have the same chance of being diagnosed during acute stage.
2. Acute-to-Chronic Ratio
Denote 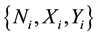 as the subjects from the i-th population who go for HIV testing over a specific period of time, where
as the subjects from the i-th population who go for HIV testing over a specific period of time, where 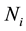 is the total number screened,
is the total number screened, 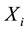 is the number with acute infection,
is the number with acute infection, 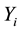 is the number with chronic infection, and the rest
is the number with chronic infection, and the rest 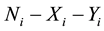 subjects are free of infection. Denote
subjects are free of infection. Denote 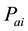 as the proportion of acute infection and
as the proportion of acute infection and 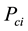 as the proportion of chronic infection. Then
as the proportion of chronic infection. Then 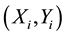 follows a multinomial distribution
follows a multinomial distribution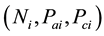 . The log likelihood over the
. The log likelihood over the  populations takes the form
populations takes the form
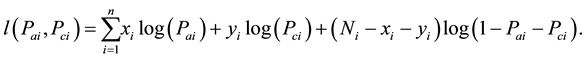 (1)
(1)
Maximum likelihood estimation (MLE) gives the sample proportions

Define 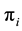 as the proportion of total infection in the i-th population, so that
as the proportion of total infection in the i-th population, so that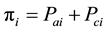 . Among the infected who seek a test, let
. Among the infected who seek a test, let  be the time from infection to HIV testing. Let
be the time from infection to HIV testing. Let 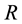 be the period from infection to detectable antibodies, also known as the antibody negative window. If
be the period from infection to detectable antibodies, also known as the antibody negative window. If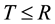 , an acute infection is detected. If
, an acute infection is detected. If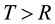 , a prevalent infection is detected. Let
, a prevalent infection is detected. Let 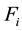 be the cumulative distribution function of
be the cumulative distribution function of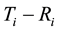 , then
, then
We define the acute-to-chronic (AC) ratio as
the odds of being diagnosed during acute stage versus chronic stage among the infected who seek an HIV test.
The distribution function 





Table 1. STD clinic data from four regions: the total number of subjects



around 0. It quantifies the chance of an infected being diagnosed within versus beyond the acute infection stage. A major attraction of the AC ratio is that it is conveniently constructed from regular testing results in STD clinics.
Note that this ratio is free of




3. MLE Inference
3.1. Common AC Ratio
If the distribution functions




The number of parameters under model (2) is

Model (2) can hold across populations even if the risks of infection are different. To test for a constant AC ratio we specify two hypotheses,




The log-likelihood ratio test statistics for testing between these two hypotheses is
where











Step 1. Generate 


Step 2. Using




Step 3. Compute the log-likelihood ratio
Step 4. Repeat Step 1 - 3 



We can also evaluate whether two groups of populations, with a common AC ratio across the populations within each group, share a common AC ratio. This may happen, for example, with one group from a developed country versus the other from a developing country, or one group with an early HIV testing campaign versus the other without such a campaign. Let 



and the log likelihood under the alternative hypothesis of group specific AC ratio is
Whether the two group of populations share a common AC ratio can be tested via the log likelihood ratio test.
3.2. AC Ratio Depending on a Factor
Some population factors, such as the population education level and income level, may affect the AC ratio. For example, in developed countries, a majority of HIV infected individuals have access to HIV testing at the time of acute infection, but access is limited in developing countries [11]. Such ecological analyses are subject to substantial confounding, but may be useful to generate hypotheses. Here we use simple logistic regression to explore the impact of a factor on the AC ratio. Let 












Maximization of (3) with respect to 
and the profile log likelihood of 
with
The parameter 
















A test of whether the AC ratio depends on 





The corresponding log likelihood ratio is
which is asymptotically 






4. Application to STD Clinic Data
4.1. Testing for a Common AC Ratio
We first investigate whether there is a common AC ratio across the four populations in Table 1. The results are shown in Figure 1. On the left is the scatter plot of the proportion of acute infection versus that of chronic infection. Each circle represents the observed proportion of acute infection versus that of the chronic infection, which is also the MLE estimate under model (1). Around each circle are the 
Figure 1. Test for common AC ratio over all 4 populations. On the left is the scatter plot of the proportion of acute infection 



the binomial distributions 











4.2. Testing for per Capita Income Related AC Ratio
For illustration, we investigate whether the AC ratio is related to the per capital income and follow (3). The estimation and testing results are presented in Figure 2. The scatter plot shows that the MLE estimates of 





Figure 2. Test for capital income related AC ratio. On the left is the scatter plot of 



through the per capital income.
References
- C. D. Pilcher, M. A. Price, I. F. Hoffman, S. Galvin, F. E. Martinson and P. N. Kazembe, et al., “Frequent Detection of Acute Primary HIV Infection in Men in Malawi,” AIDS, Vol. 18, No. 3, 2004, pp. 517-524. http://dx.doi.org/10.1097/00002030-200402200-00019
- UNAIDS, “HIV Voluntary Counseling and Testing: A Gateway to Prevention and Care,” Joint United Nations Program on HIV/AIDS, Geneva, 2002.
- C. D. Pilcher, J. J. Eron, P. L. Vemazza, M. Battegay, T. Harr and S. Yerly, “Sexual Transmission during the Incubation Period of Primary HIV Infection,” Journal of American Medical Association, Vol. 286, No. 14, 2001, pp. 1713-1714. http://dx.doi.org/10.1001/jama.286.14.1713
- T. Flanigan and K. T. Tashima, “Diagnosis of Acute HIV Infection: It’s Time to Get Moving,” Annals of Internal Medicine, Vol. 134, No. 1, 2001, pp. 75-77. http://dx.doi.org/10.7326/0003-4819-134-1-200101020-00017
- R. Brookmeyer and T. C. Quinn, “Estimation of Current Human Immunodeficiency Virus Incidence Rates From a Cross-Sec- tional Survey Using Diagnosis Tests,” American Journal of Epidemiology, Vol. 141, No. 2, 1995, pp. 166-172.
- C. D. Pilcher, S. A. Fiscus, T. Q. Nguyen, E. Foust, L. Wolf and D. Williams, “Detection of Acute Infections during HIV Testing in North Carolina,” New England Journal of Medicine, Vol. 352, No. 18, 2005, pp. 1873-1883. http://dx.doi.org/10.1056/NEJMoa042291
- J. D. Klausner, R. M. Grant and C. K. Kent, “Detection of Acute HIV Infections,” New England Journal of Medicine, Vol. 353, No. 6, 2005, pp. 631-633. http://dx.doi.org/10.1056/NEJM200508113530620
- A. M. Shahkolahi and P. Chiliade, “Early Diagnosis of HIV Infection at Whitman Walker Clinic STD Program Using NAATs on Pooled Blood Samples,” National STD Prevention Conference, 9 May 2006.
- S. Lindback, R. Thorstensson, A. C. Karlsson, M. Von Sydow, L. Falmholc and A. Blaxhult, “Diagnosis of Primary HIV-1 Infection and Duration of Follow-Up After HIV Exposure,” AIDS, Vol. 14, 2000, pp. 2333-2339. http://dx.doi.org/10.1097/00002030-200010200-00014
- E. W. Fiebig, D. J. Wright, B. D. Rawal, P. E. Garret, R. T. Schumacher and L. Peddada, “Dynamics of HIV Viremia and Antibody Seroconversion in Plasma Donors: Implications for Diagnosis and Staging of Primary HIV Infection,” AIDS, Vol. 17, No. 13, 2003, pp. 1871-1879. http://dx.doi.org/10.1097/00002030-200309050-00005
- T. A. Schacker, C. Collier, J. Hughes, T. Shea and L. Corey, “Clinical and Epidemiologic Features of Primary HIV Infection,” Annals of Internal Medicine, Vol. 125, No. 4, 1996, pp. 257-264. http://dx.doi.org/10.7326/0003-4819-125-4-199608150-00001
















