Open Journal of Statistics
Vol.3 No.6(2013), Article ID:41527,5 pages DOI:10.4236/ojs.2013.36045
Estimation of a Type of Form-Invariant Combined Signals under Autoregressive Operators
1College of Aerospace and Materials Engineering, National University of Defense Technology, Changsha, China
2College of Science, National University of Defense Technology, Changsha, China
Email: *yszhangnudt@163.com
Copyright © 2013 Yinsheng Zhang et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2013 are reserved for SCIRP and the owner of the intellectual property Yinsheng Zhang et al. All Copyright © 2013 are guarded by law and by SCIRP as a guardian.
Received July 5, 2013; revised August 5, 2013; accepted August 12, 2013
Keywords: Form-Invariant Signals; Autoregressive Operator; Autoregressive Noise; Parameter Estimation
ABSTRACT
We focus on a type of combined signals whose forms remain invariant under the autoregressive operators. To extract the true signal from the autoregressive noise, we develop a strategy to separate parameters and use a two-step least squares approach to estimate the autoregressive parameters directly and then further give the estimate of the signal parameters. This method overcomes the difficulty that the autoregressive noise remains unknown in other methods. It can effectively separate the noise and extract the true signal. The algorithm is linear. The solution of the problem is computationally cheap and practical with high accuracy.
1. Introduction
The reconstruction of signals from color noises is a general problem in data processing. Effective solutions to this problem have a wide range of applications in many fields, such as radar signal processing, image enhancement, speech coding and data mining. Usually, different strategies are applied for different scenarios and assumptions. The parameter estimation of signals with autoregressive (i.e., AR) noises is a class of typical problems.
The approaches can be raised from several perspectives. Firstly, as far as the parameters estimation of the AR model is concerned, Harry H. Kelejian et al. [1] discussed the estimation of the autoregressive parameter in a widely considered spatial autocorrelation model. They suggested a generalized moment estimator that is computationally simple irrespective of the sample size. Sascha Korl et al. [2] considered this problem from a graphical-model viewpoint. In particular, they demonstrate joint estimation of AR coefficients, innovation variance and noise variance. Wing-Keung Wong et al. [3] presented the way of estimating parameters in AR models with asymmetric innovations. Jinfang Liu et al. [4] raised a self-tuning weighted measurement fusion Kalman filter to estimate the parameters for single channel autoregressive moving average signals with colored noise when the model parameters and noise statistics are unknown.
Secondly, for the noise removal and signal extraction, the simplest approach is to ignore the coloring of the noise and use methods such as least squares that assume white noise. This approach is obviously inappropriate. Mihalis Samonas et al. [5] used a self-consistent restoration peak preserving algorithm to eliminate the high level additive colored Gaussian noise. David Kozel et al. [6] proposed a spectral subtraction algorithm for reducing colored noise from noise-corrupted speech, however with a limitation of the requirement of a favorable signal to noise ratio as with all spectral subtraction algorithms. Jesper Højvang Jensen et al. [7] derived the signal amplitude and noise covariance matrix estimator with colored Gaussian noise and extended the existed singlesinusoid algorithm to multiple sinusoids. The method does not consider the estimation of the noise covariance matrix and the sinusoid amplitudes as two separate tasks, but rather estimates them jointly.
In addition to the above two types of methods, the most effective way is apparently to derive the AR parameters and the true signal parameters simultaneously. This is difficult to perform in the general case. In this contribution, as for a wide class of signals which are form-invariant under the autoregressive operators, we propose a method of parameters separation and then use the idea to give the estimates of both the AR and the signal parameters. This approach can solve the above problem and improve the estimation accuracy of the true signal.
2. Problem Description
2.1. Signal-Noise Model
Consider the observation  satisfies the following model
satisfies the following model
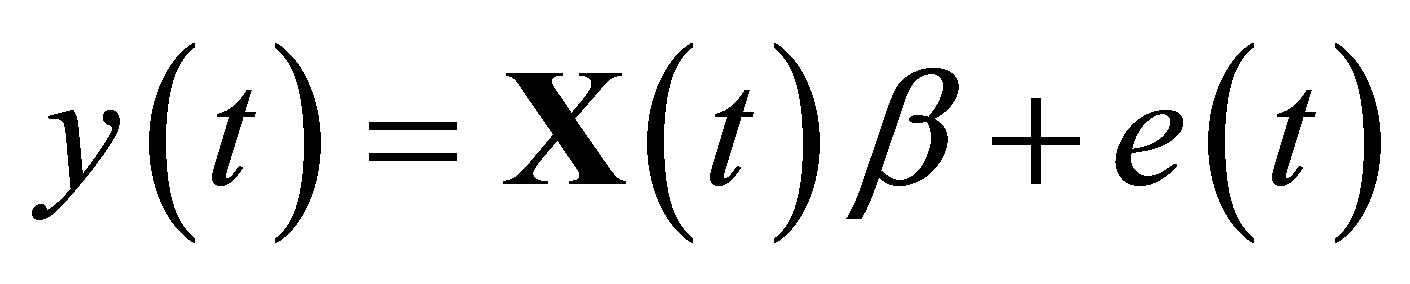 (1)
(1)
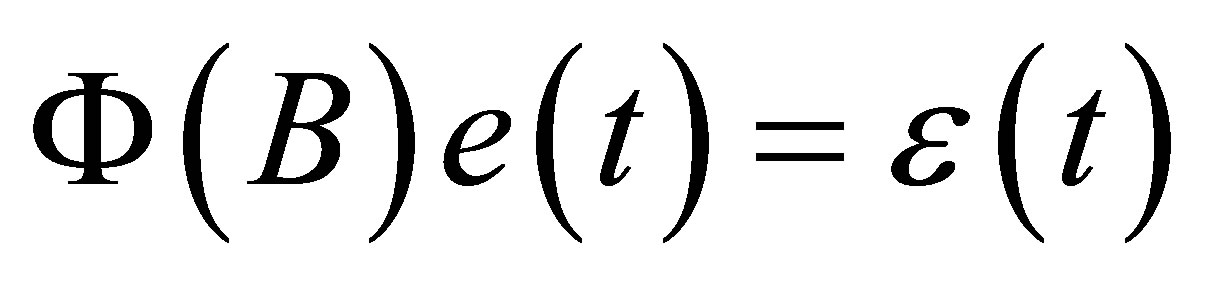 (2)
(2)
where
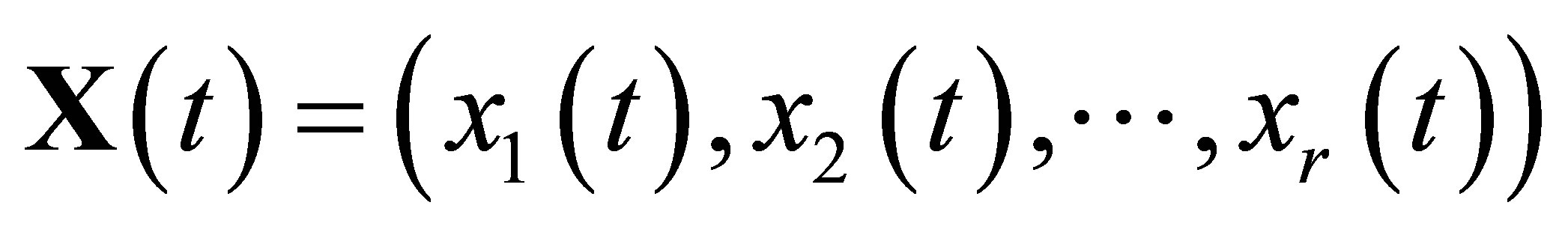 ,
,
 .
.
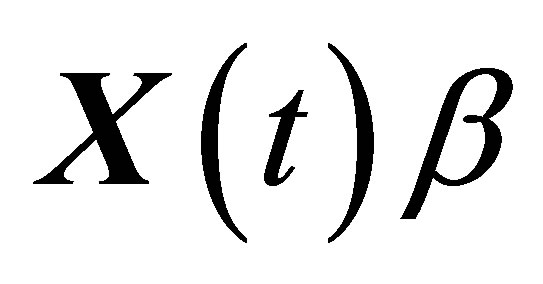 is the true signal component of
is the true signal component of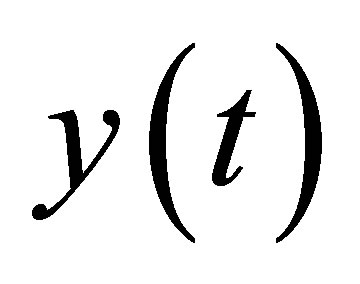 , and
, and ![]() is the noise in
is the noise in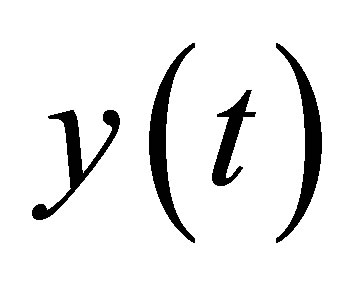 . Suppose the noise is the stationary correlated autoregressive
. Suppose the noise is the stationary correlated autoregressive 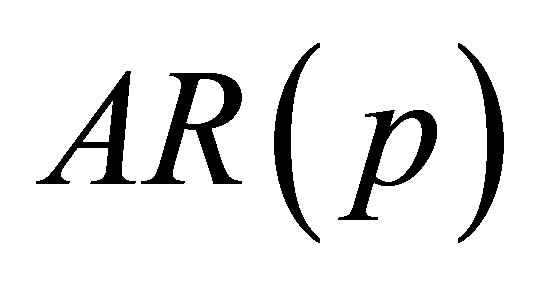 model, i.e.,
model, i.e.,
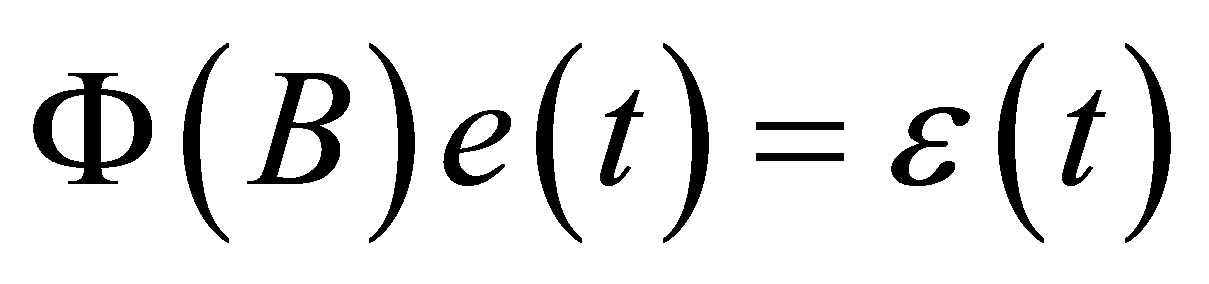 ,
, 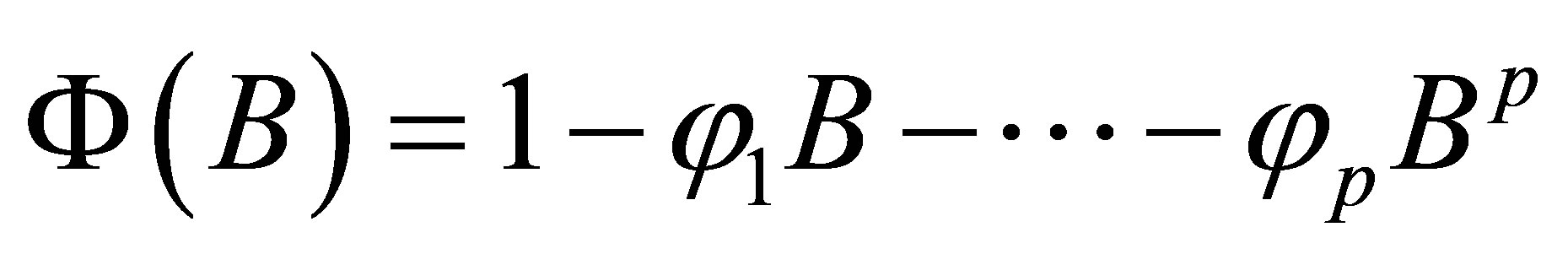 where B is a one-step backward operator, and
where B is a one-step backward operator, and
 ,
,
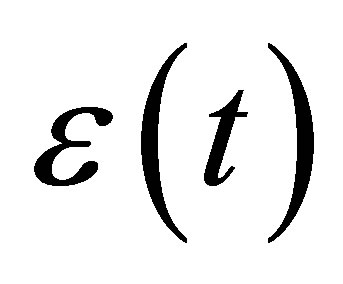 is zero-mean white noise. Assume we have the observation data
is zero-mean white noise. Assume we have the observation data 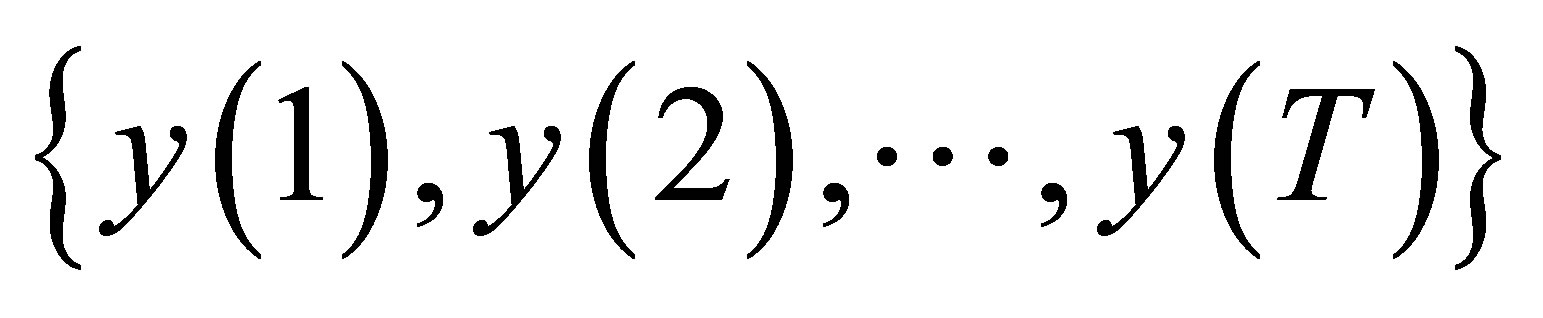 of
of ![]() instants. Now the problem is how to give the accurate estimation of the unknown parameters
instants. Now the problem is how to give the accurate estimation of the unknown parameters ![]() and
and 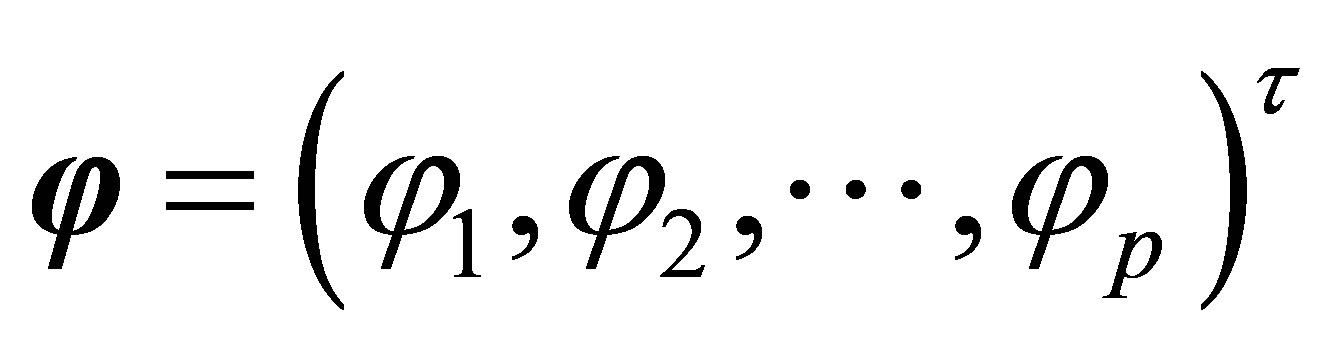 for the model (1) and (2).
for the model (1) and (2).
The vector form of model (1) is as following.
 (3)
(3)
where 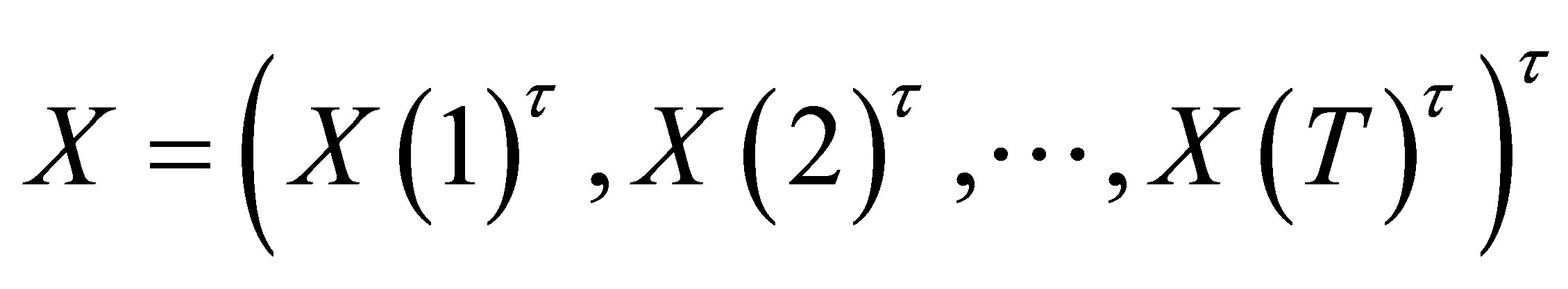 is a known
is a known 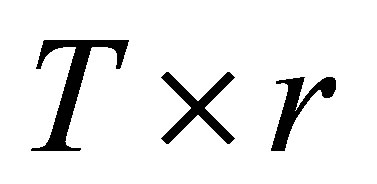 column-full-rank matrix, which is usually called the design matrix in linear regression analysis, and
column-full-rank matrix, which is usually called the design matrix in linear regression analysis, and
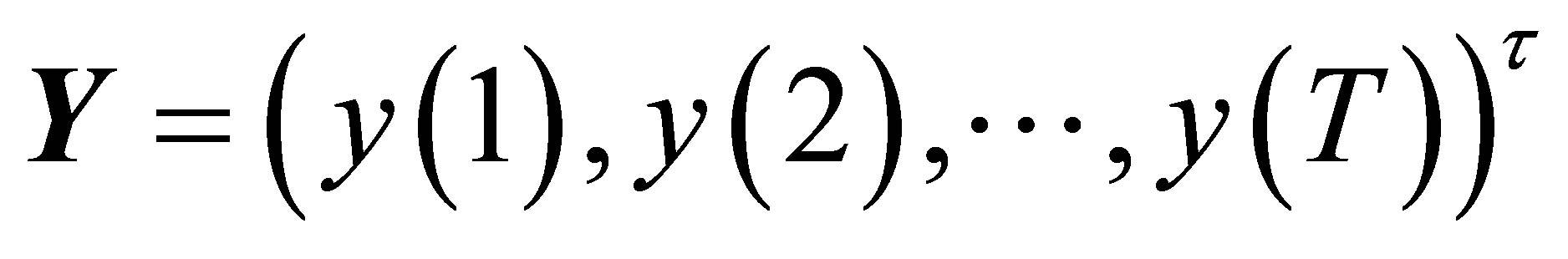 ,
,
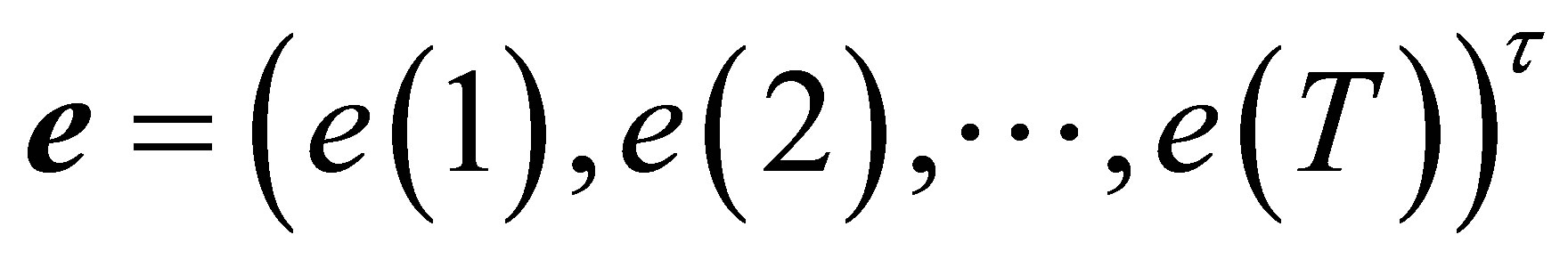 .
.
As e is a stationary correlated noise, the least squares estimates 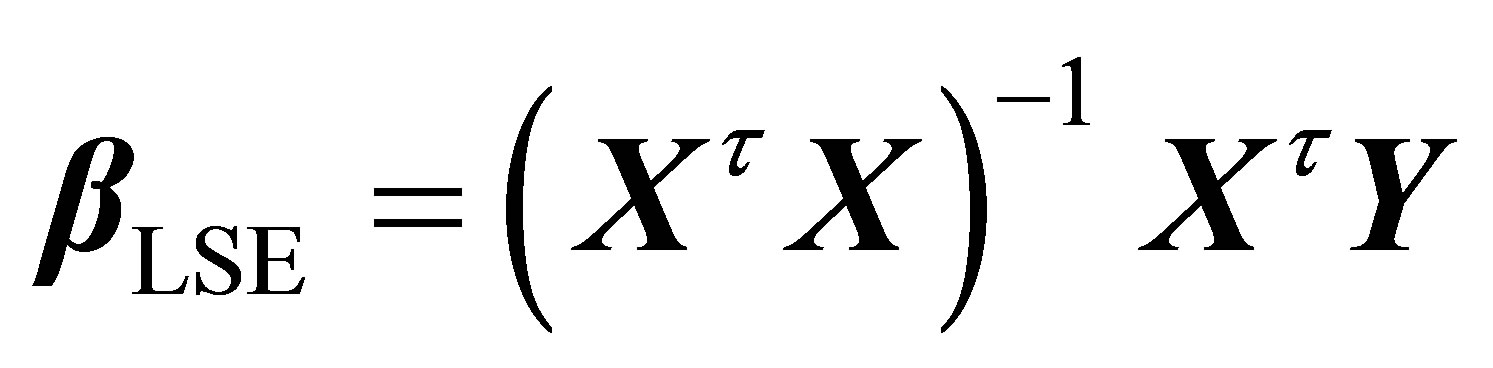 will no longer possess the favorable properties as usual. In this case, the weighted least squares estimates
will no longer possess the favorable properties as usual. In this case, the weighted least squares estimates
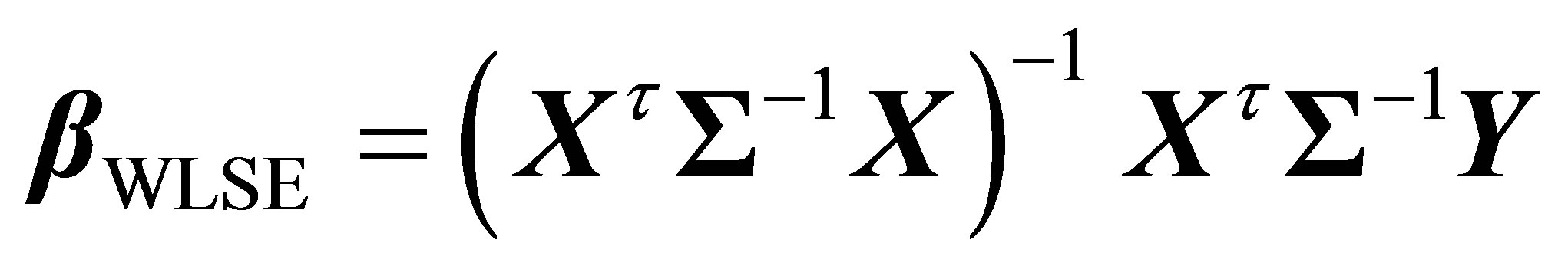
should be used, which requires the knowledge of the covariance matrix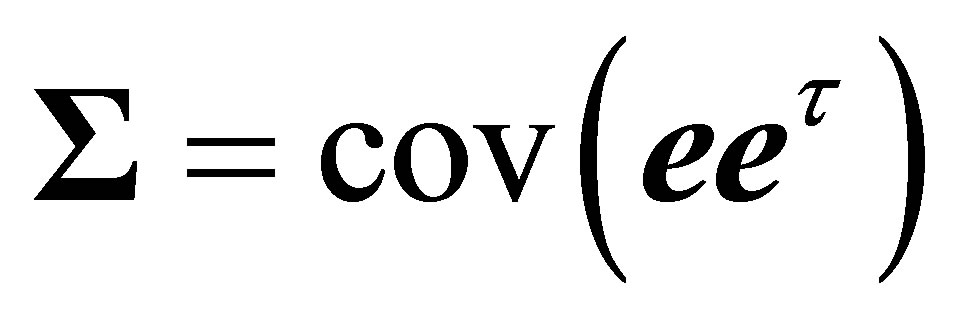 . However,
. However, ![]() is not observable in practice, thus the solution to
is not observable in practice, thus the solution to 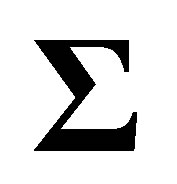 is rather difficult. To solve this problem, we need to find another way. Signals and noises can usually be expressed as parametric models, thus it can be summed up as parameter estimation issues of the signal-noise models. In the following part of this paper, we will give the estimates of both the AR and the signal parameters for a wide class of signals which are form-invariant under the autoregressive operators.
is rather difficult. To solve this problem, we need to find another way. Signals and noises can usually be expressed as parametric models, thus it can be summed up as parameter estimation issues of the signal-noise models. In the following part of this paper, we will give the estimates of both the AR and the signal parameters for a wide class of signals which are form-invariant under the autoregressive operators.
2.2. The Form-Invariant Signals Under ![]()
For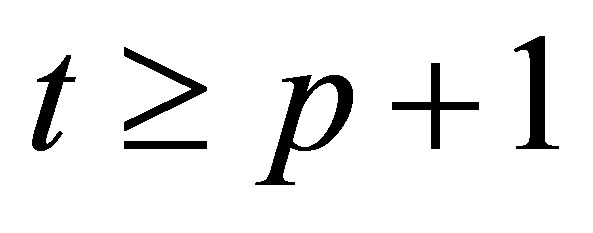 , we impact the autoregressive operator
, we impact the autoregressive operator  on both sides of (1) at the same time and get
on both sides of (1) at the same time and get
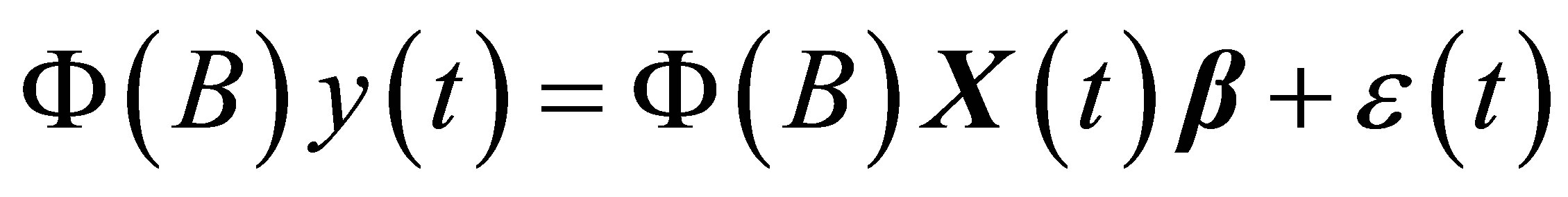 (4)
(4)
where
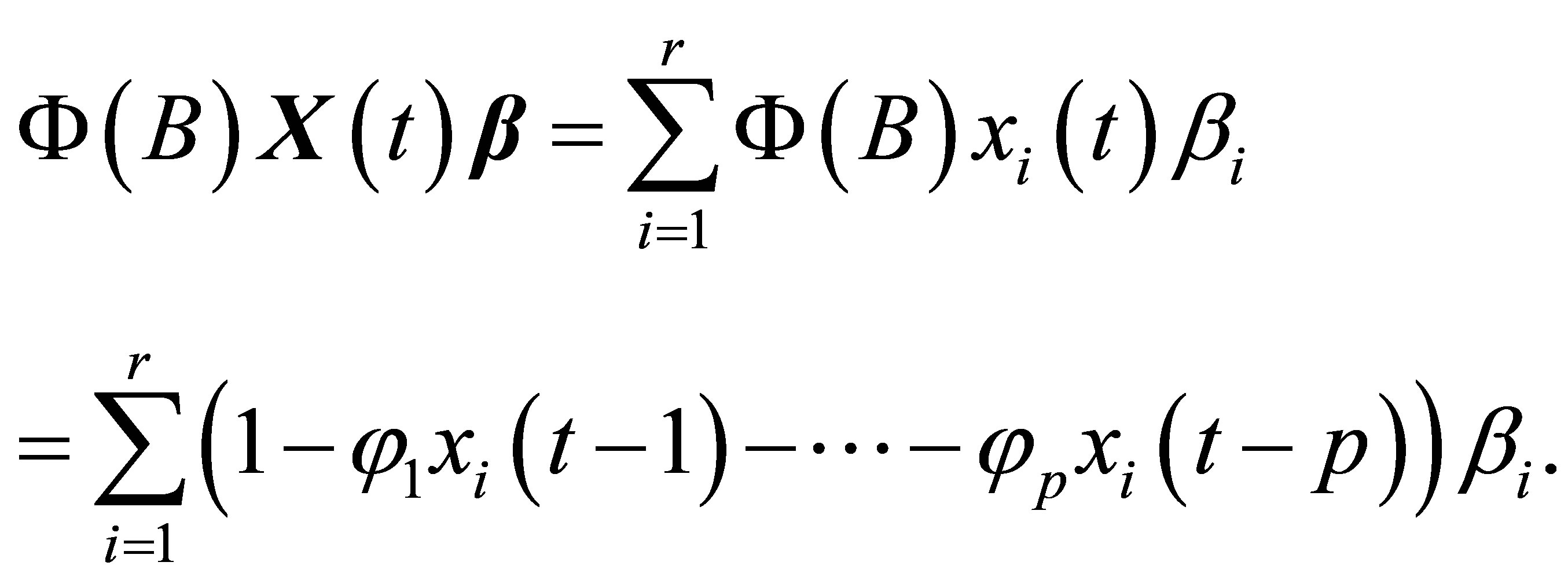
In the procedure of the above transformation, if the true signal 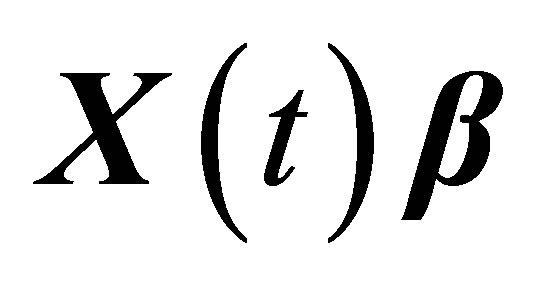 satisfies the following property:
satisfies the following property:
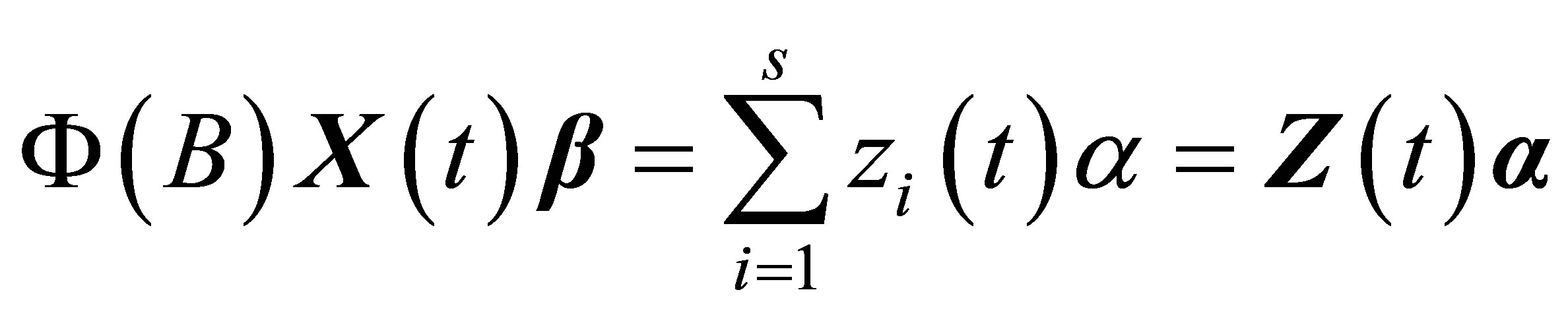 (5)
(5)
where
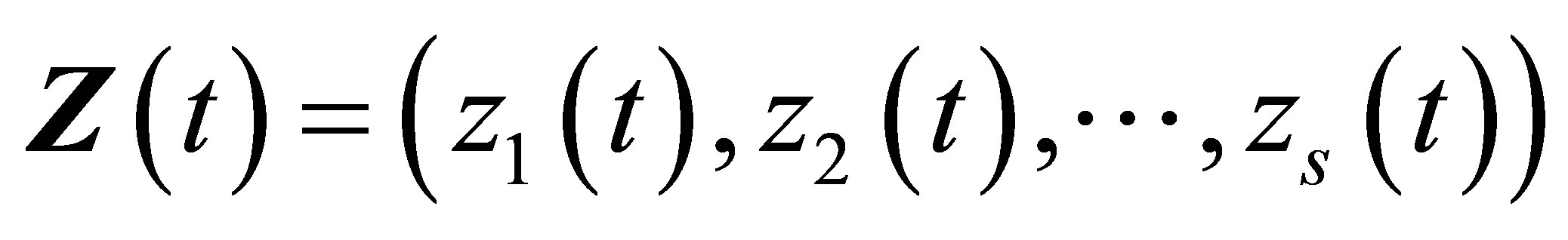 ,
,
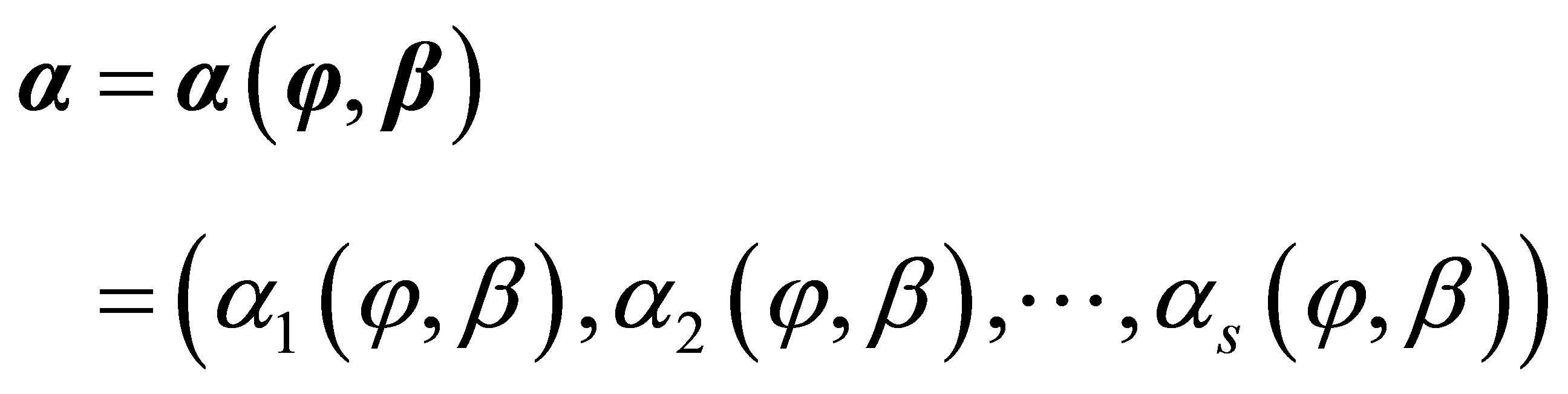
is the vector function of![]() , and the design matrix
, and the design matrix
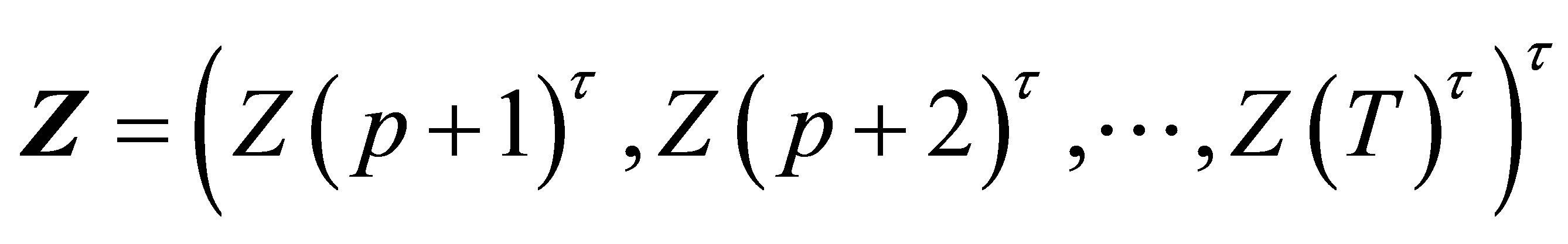
made up by the transformed 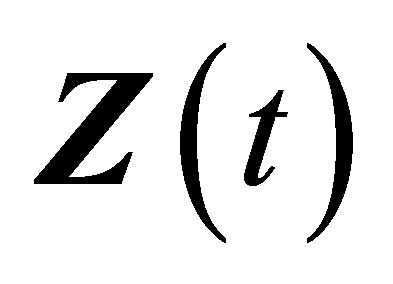 remains the characteristics of column-full-rank, then we call
remains the characteristics of column-full-rank, then we call 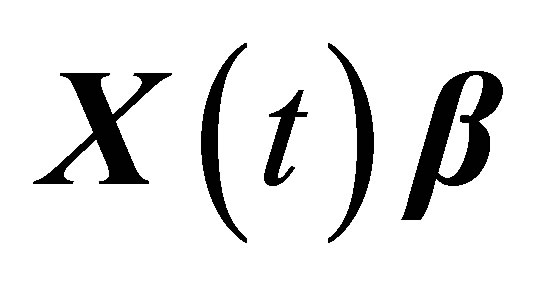 as the form-in-variant signal under the function of
as the form-in-variant signal under the function of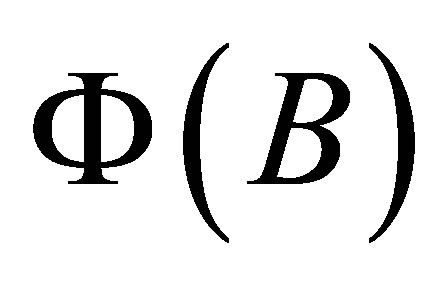 . Here the design matrix remains column-full-rank under
. Here the design matrix remains column-full-rank under 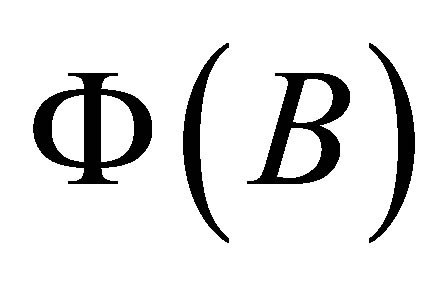 is the key factor, which will be shown clearly in the following section. One of an important special case for Equation (5) is that:
is the key factor, which will be shown clearly in the following section. One of an important special case for Equation (5) is that:
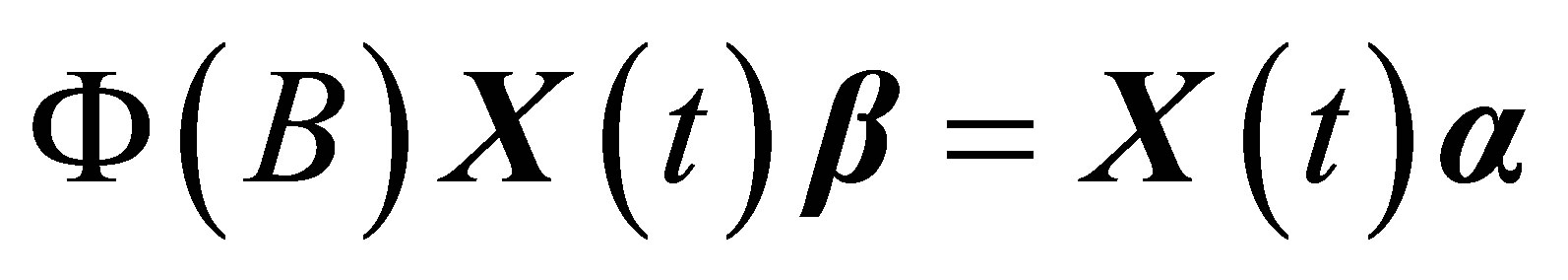 (6)
(6)
That is, the design matrix remains completely the same under the impact of .
.
Now we give a few examples of the form-invariant signals.
A. Polynomial signal Assume , then
, then

where
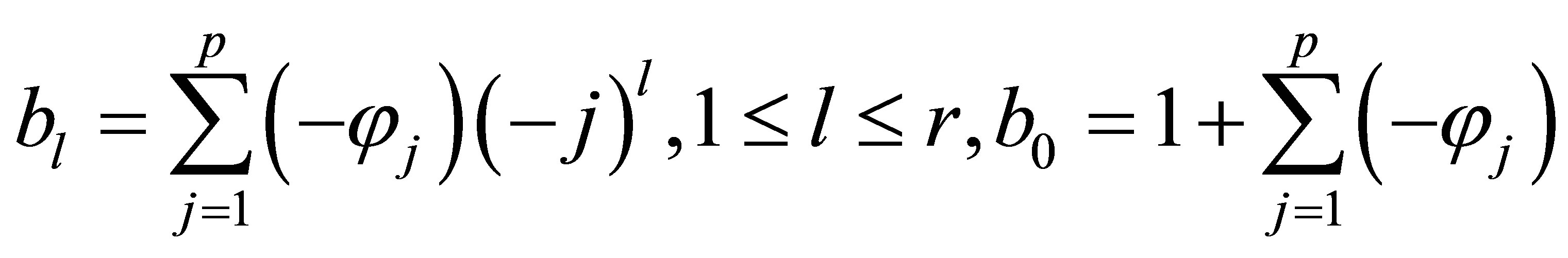 Let
Let
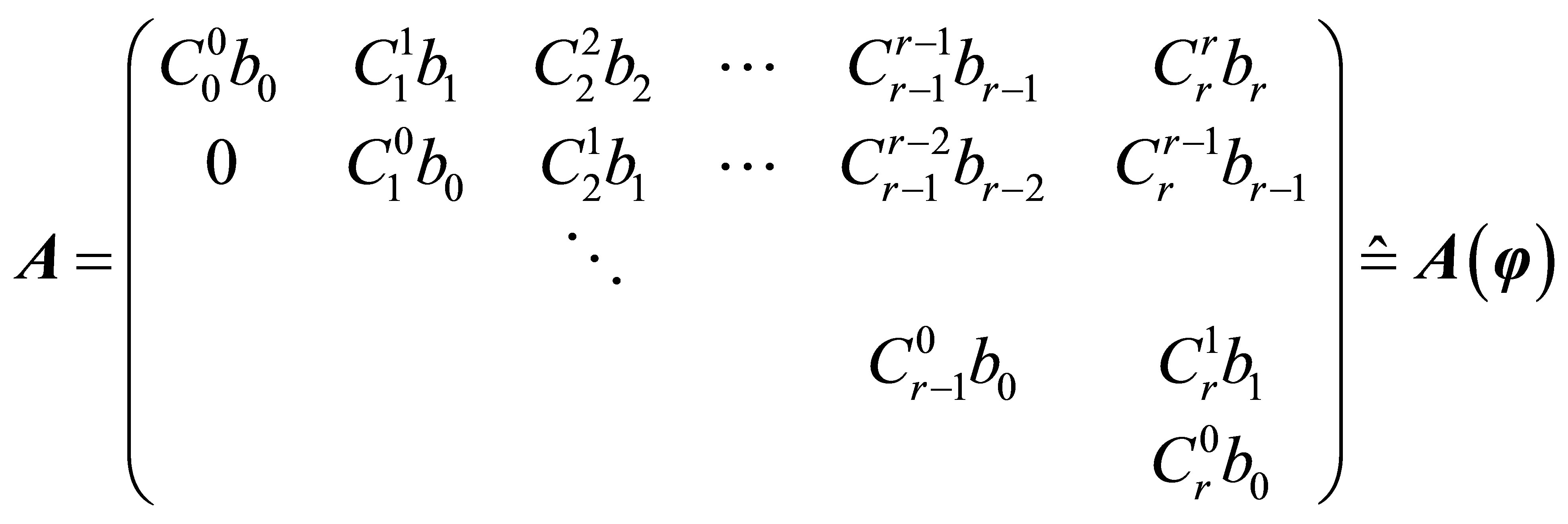
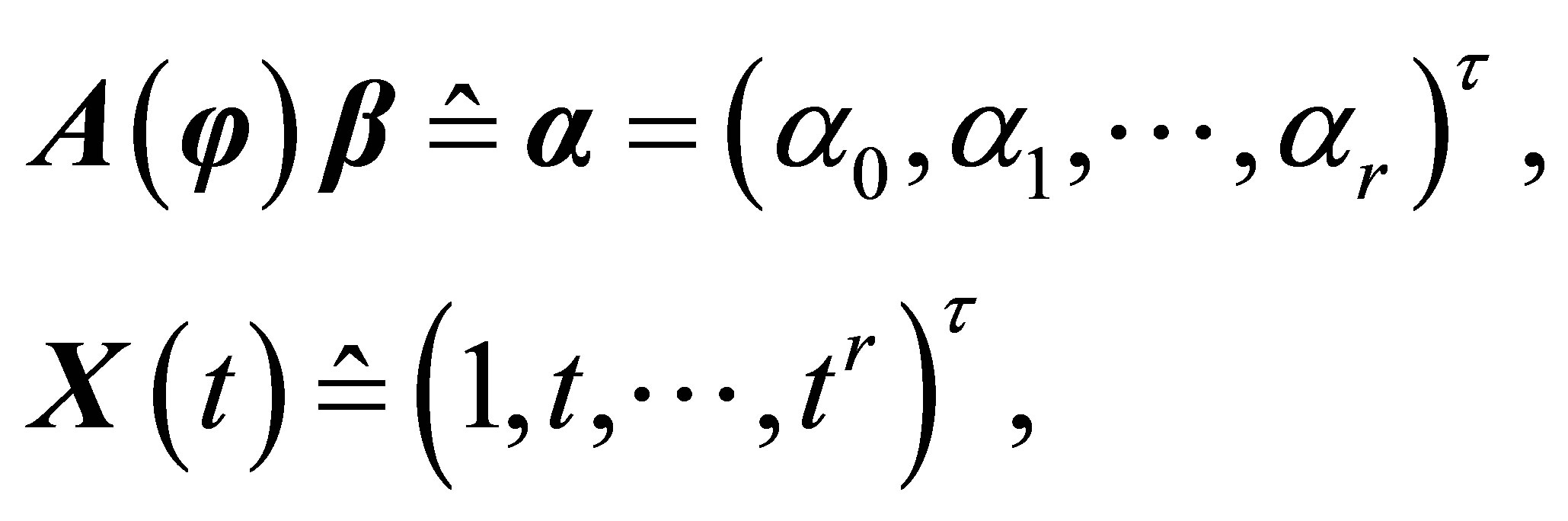
Then we have , Therefore,
, Therefore, 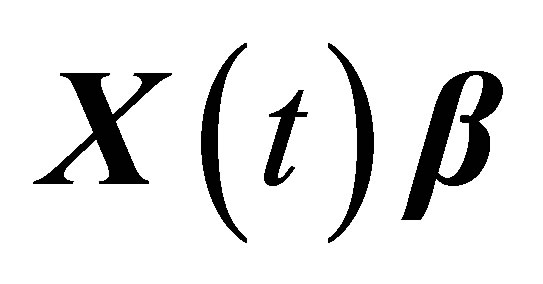 is the form-invariant signal satisfying Equation (6).
is the form-invariant signal satisfying Equation (6).
B. Trigonometric function signal Suppose
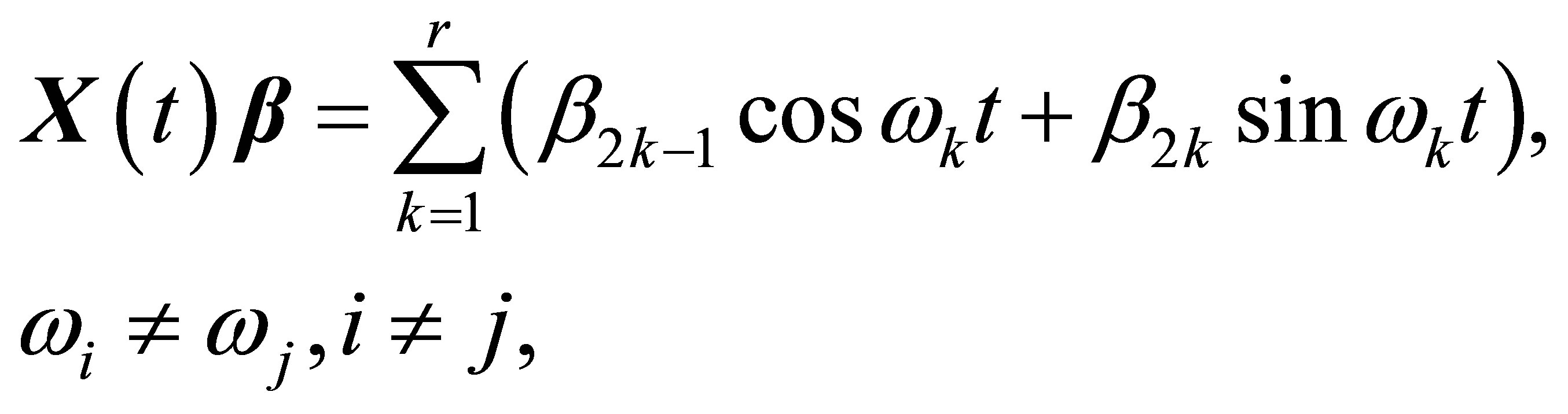
then
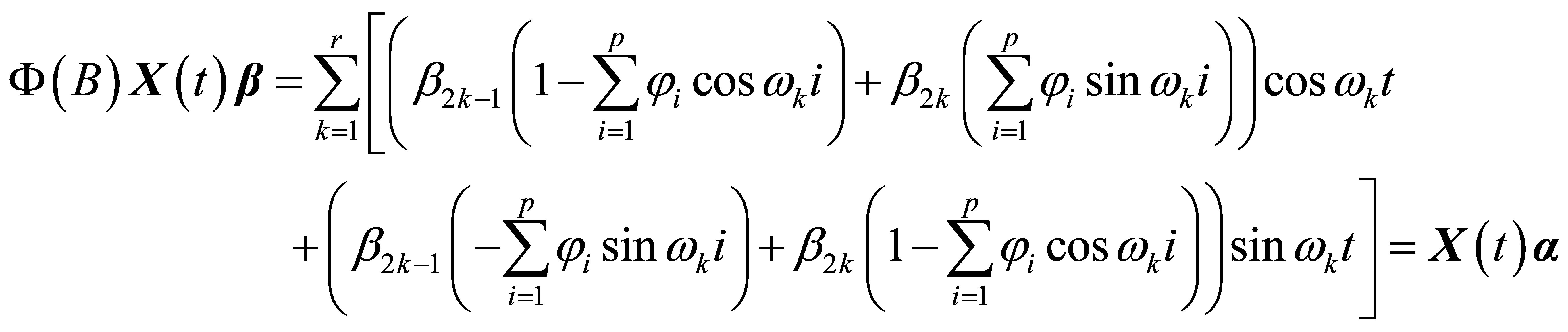
where
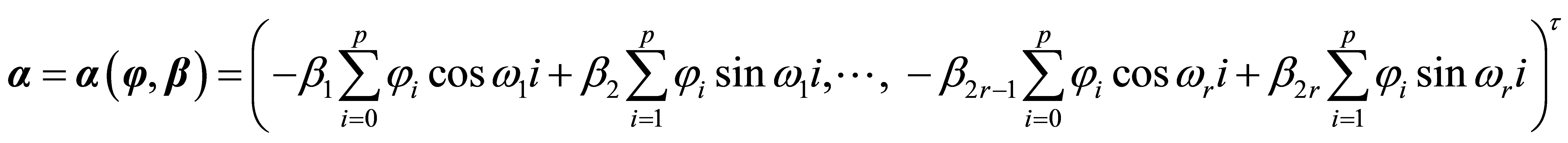
so 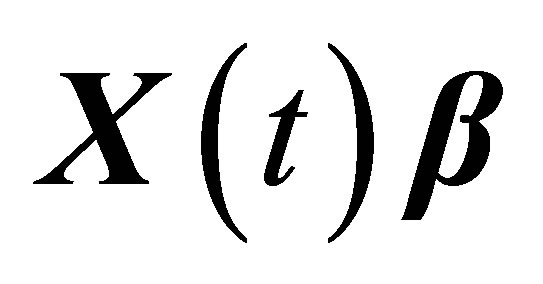 is a form-invariant signal which satisfies Equation (6).
is a form-invariant signal which satisfies Equation (6).
C. Exponential function signal Suppose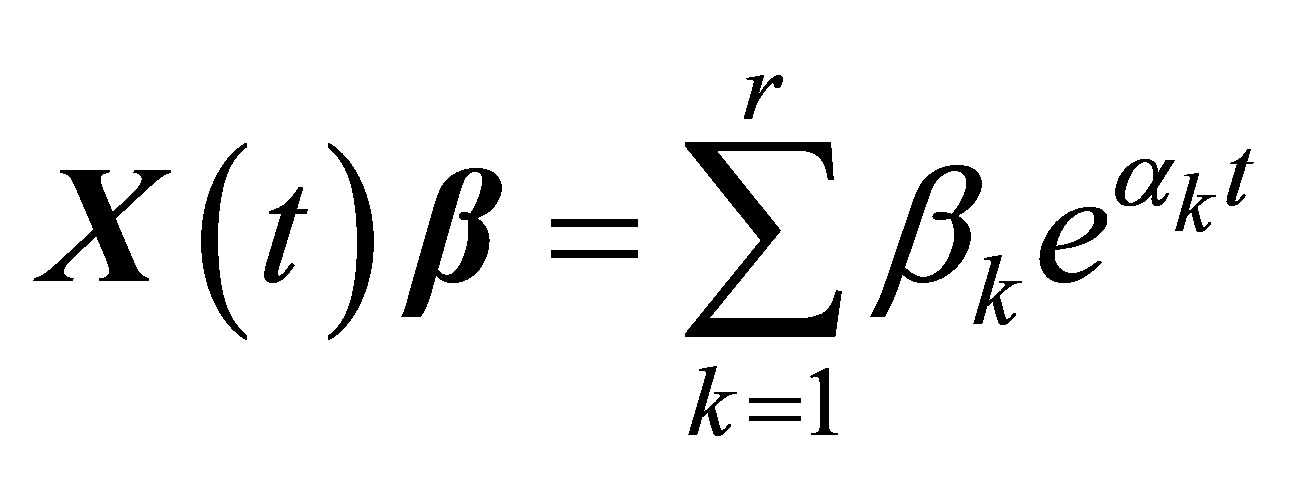 ,
,
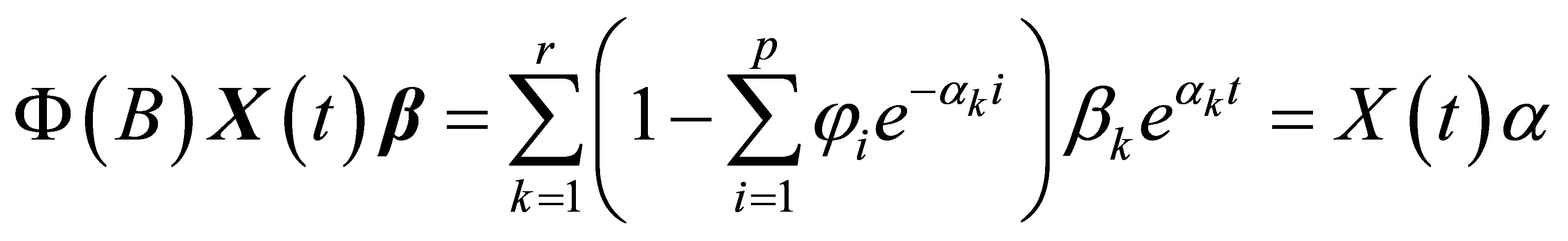 where
where
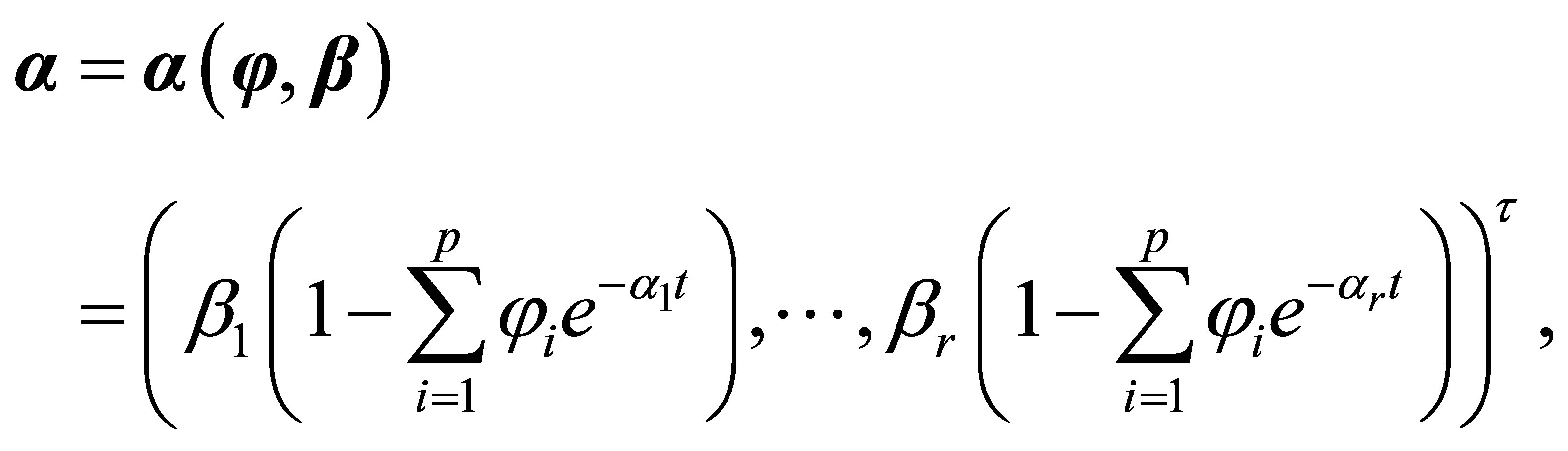
therefore, 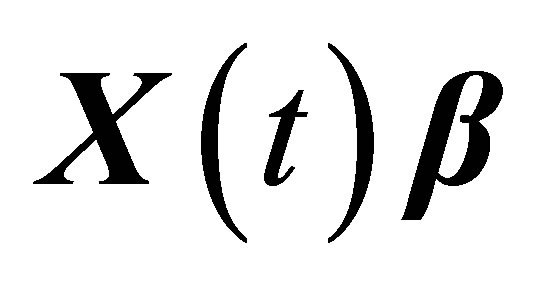 is another form-invariant signal satisfying Equation (6).
is another form-invariant signal satisfying Equation (6).
Finally, we can come to the statement that the mixed signals composed of the signals above linearly (e.g.,
 ) are also form-invariant. Besides the signals we mentioned above, there is also plenty of other form-invariant signals satisfying Equation (5) or Equation (6) in practice.
) are also form-invariant. Besides the signals we mentioned above, there is also plenty of other form-invariant signals satisfying Equation (5) or Equation (6) in practice.
3. Parameters Estimation
3.1. The Estimation of Parameter ![]()
From the discussion above, for the form-invariant signal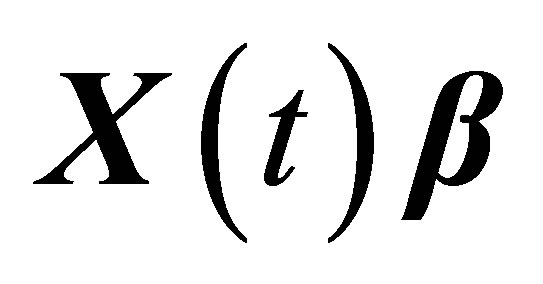 , the linear model (1) becomes the following equation under the autoregressive operator
, the linear model (1) becomes the following equation under the autoregressive operator :
:
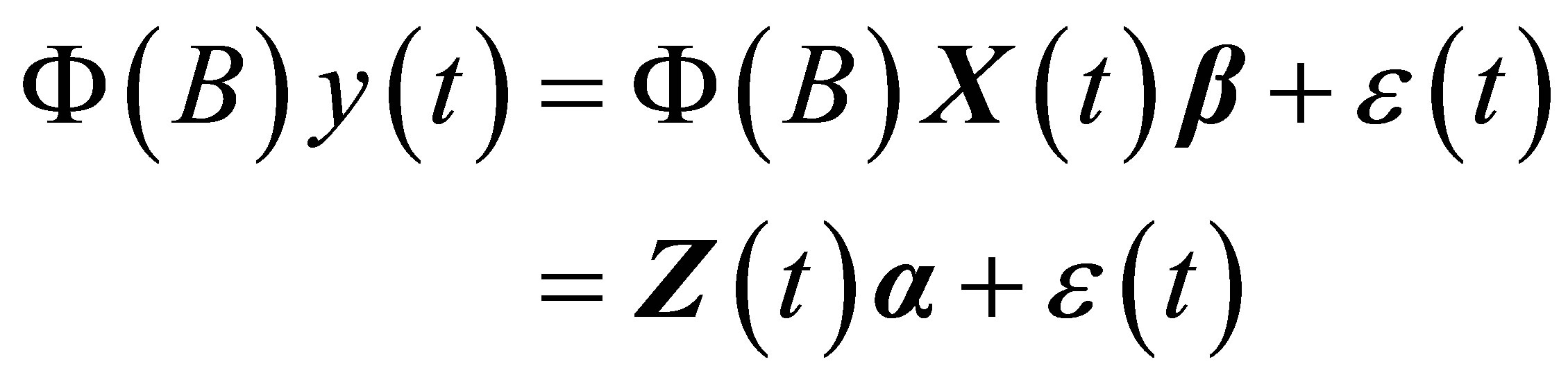 (7)
(7)
The vector form of Equation (7) is
 (8)
(8)
where
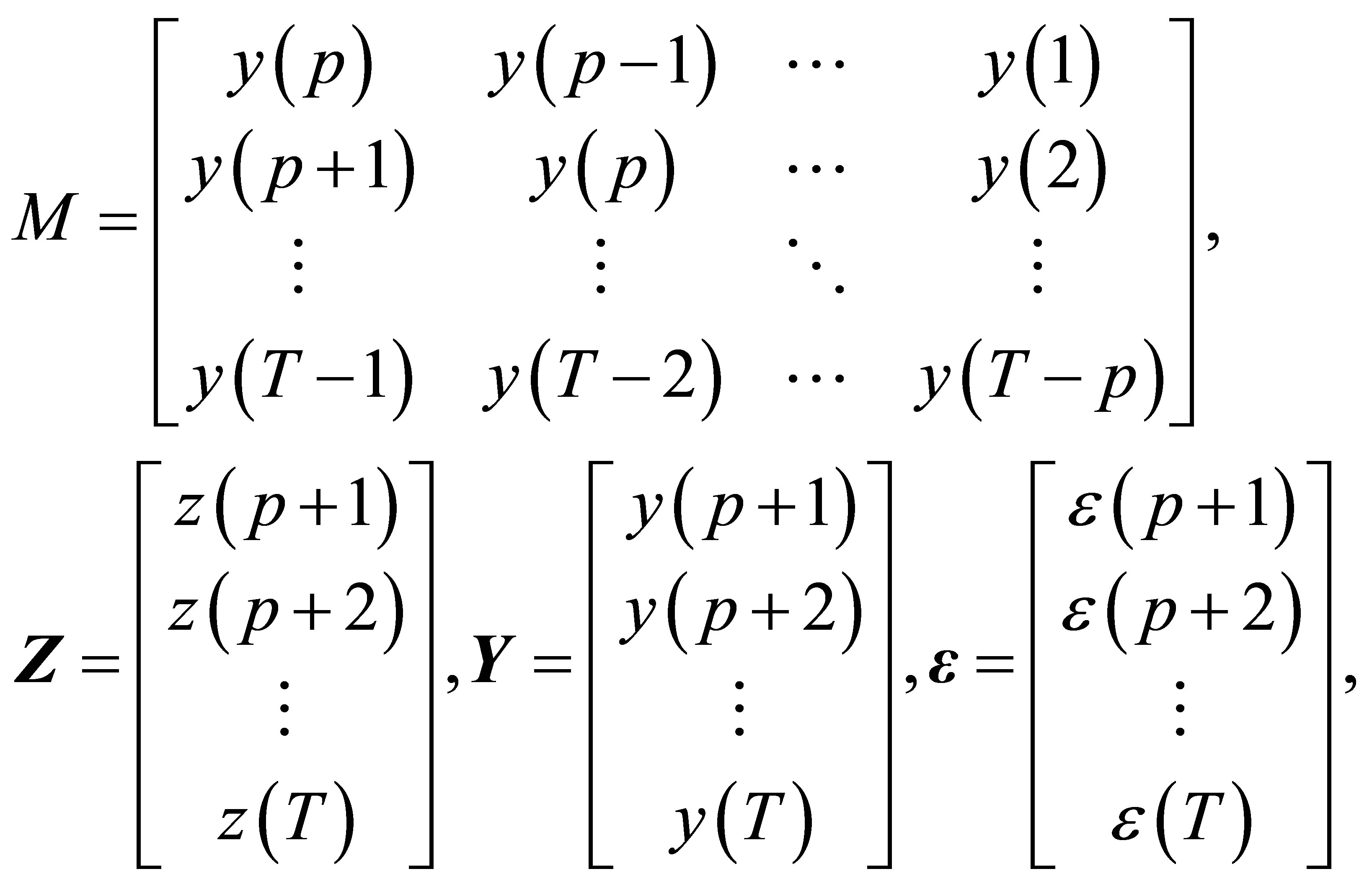
Since the design matrix  of the form-invariant signal remains column-full-rank after the transform of
of the form-invariant signal remains column-full-rank after the transform of , the least squares solution “in form” of Equation (8) is:
, the least squares solution “in form” of Equation (8) is:
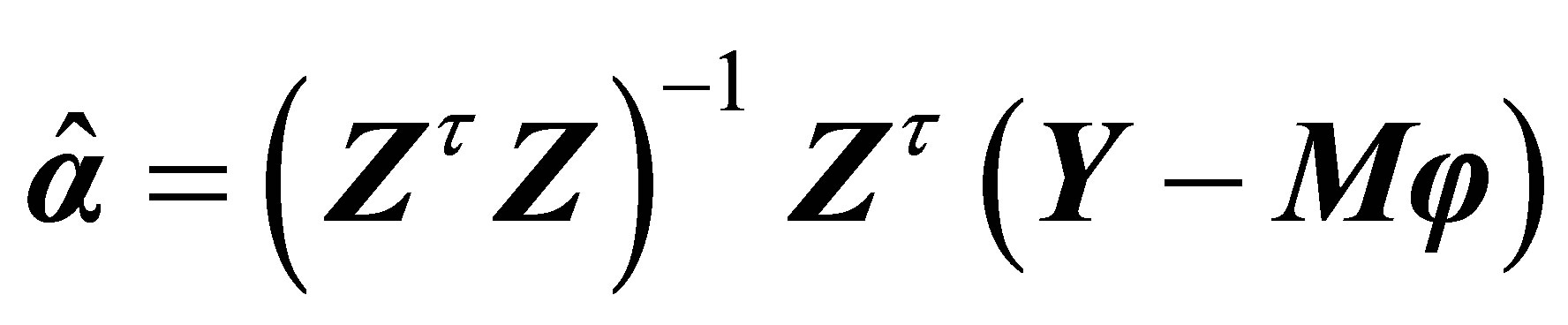 (9)
(9)
The solution is called “in form” because  in
in 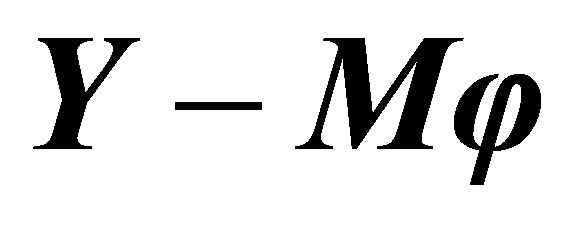 is unknown. And the residual sum of squares is
is unknown. And the residual sum of squares is
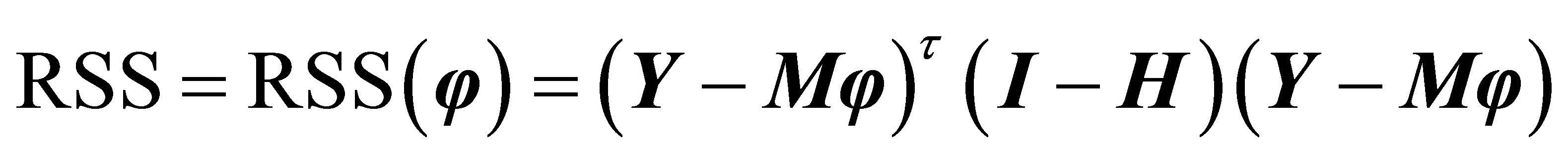 (10)
(10)
where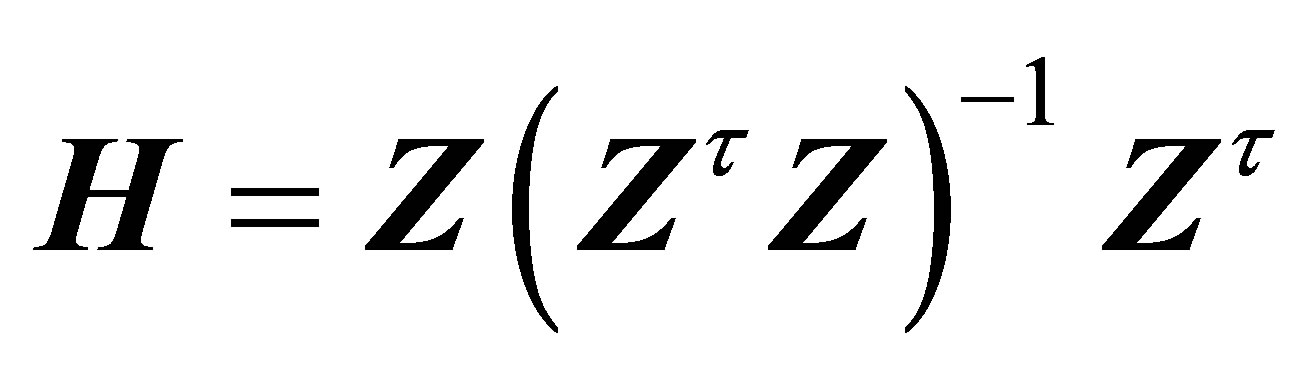 . Note that
. Note that 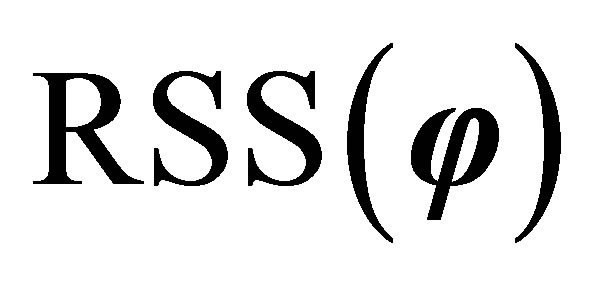 is a quadratic function of
is a quadratic function of , so there exists the unique
, so there exists the unique  satisfying
satisfying
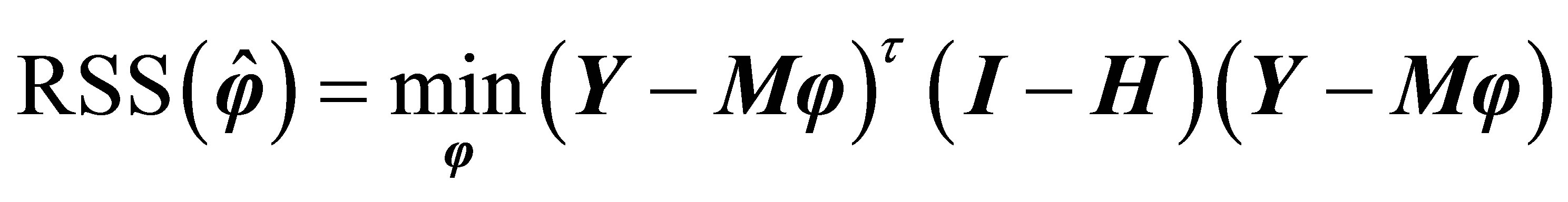 (11)
(11)
The solution to Equation (11) is:
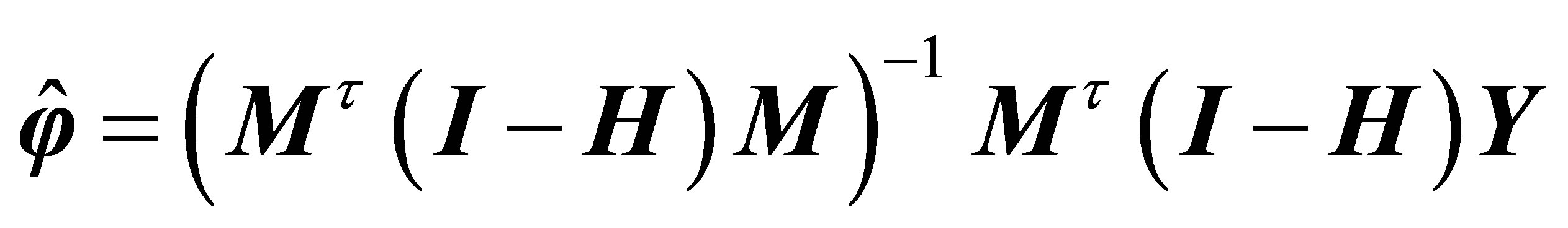 (12)
(12)
The above procedure to get  actually involves twice the solution to the minimum of least squares residuals, therefore Equation (12) is also called the two-step least squares estimate of
actually involves twice the solution to the minimum of least squares residuals, therefore Equation (12) is also called the two-step least squares estimate of .
.
3.2. The Estimation of Parameter β
After the acquisition of the estimate  of
of , from Equation (4), we can regard the estimation of
, from Equation (4), we can regard the estimation of ![]() as the parameter estimation of the following linear model:
as the parameter estimation of the following linear model:
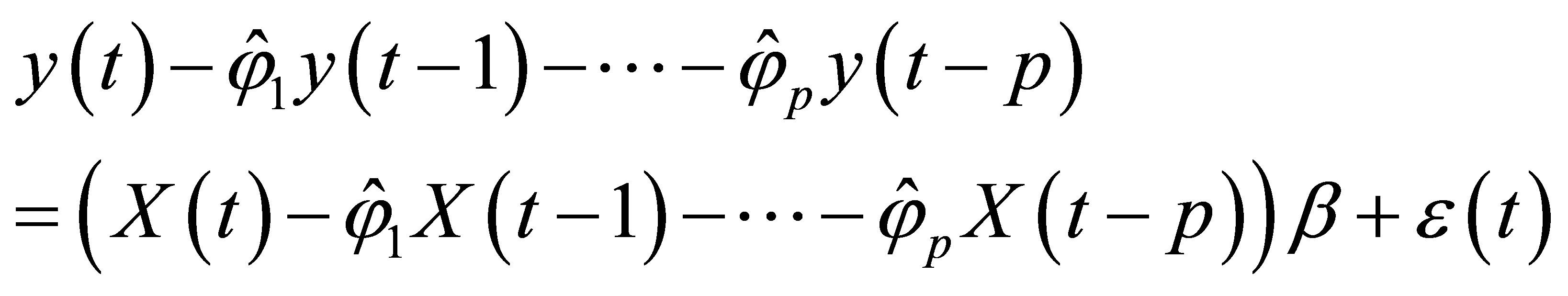 (13)
(13)
The vector form of Equation (13) is
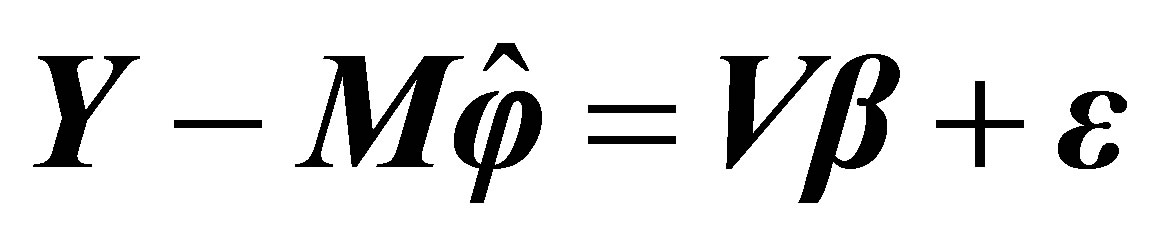 (14)
(14)
where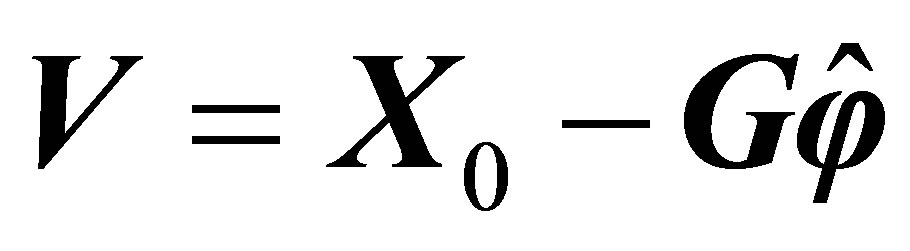 ,
,  ,
,
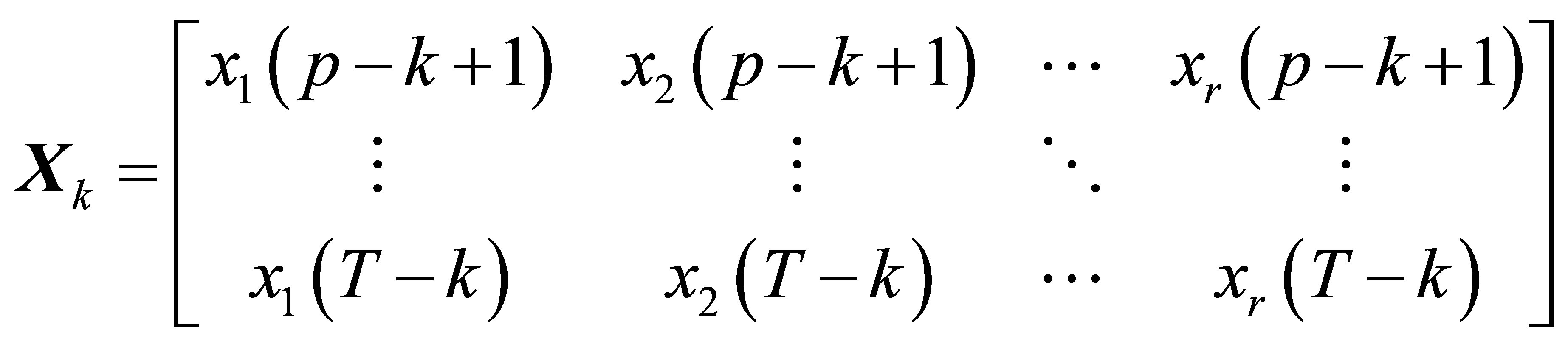 ,
,
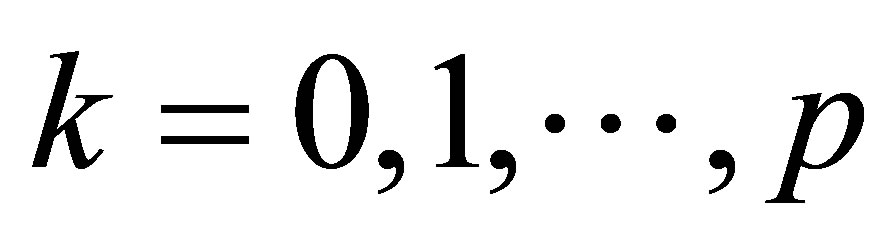 .
.
From Equation (14), the estimation of the parameter ![]() is
is
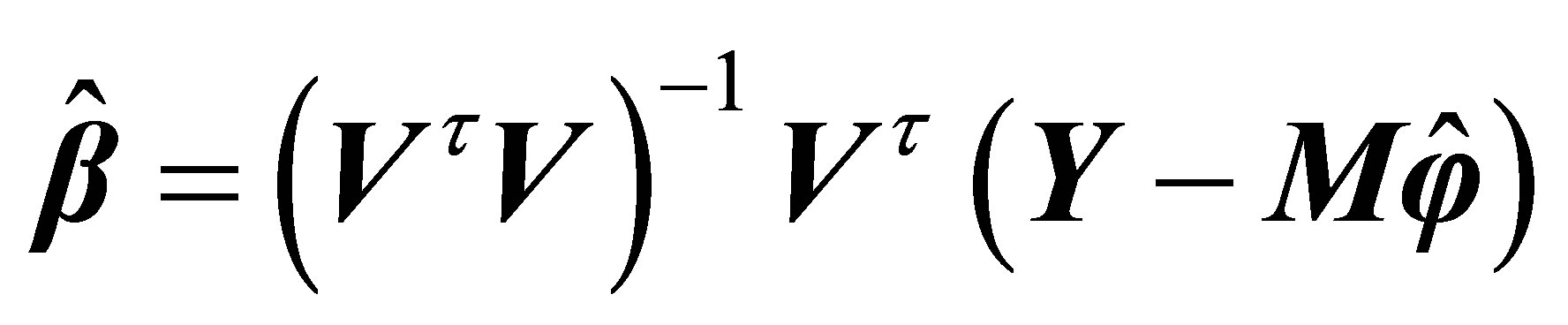 (15)
(15)
Furthermore, from Equation (15) and (14) we have
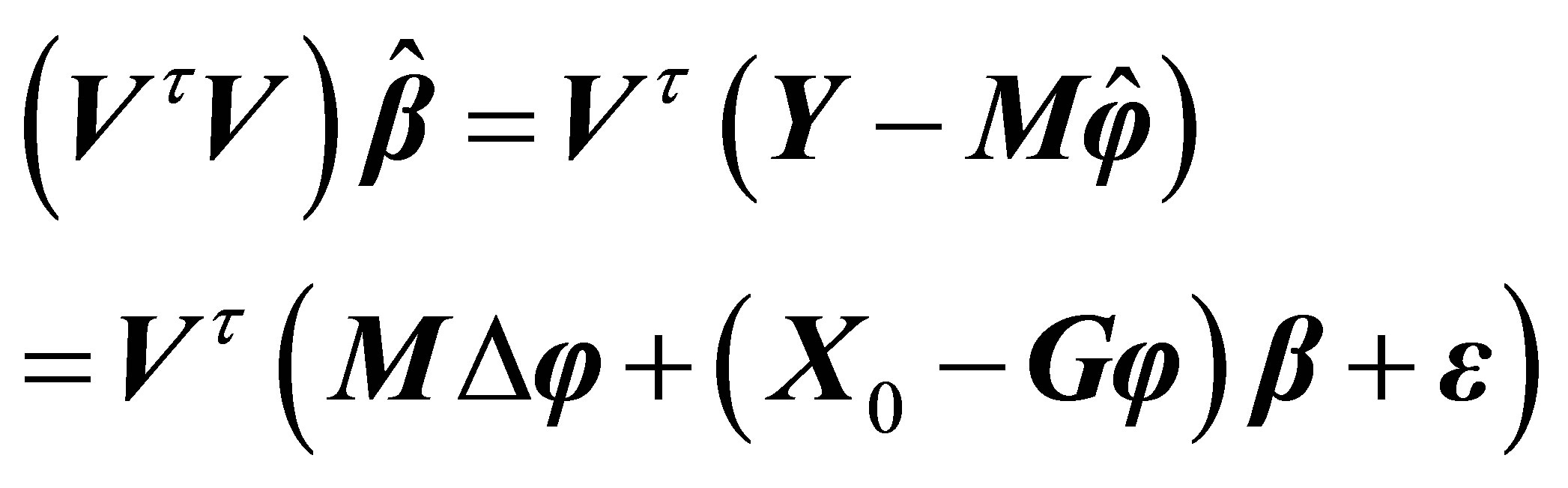 (16)
(16)
thus
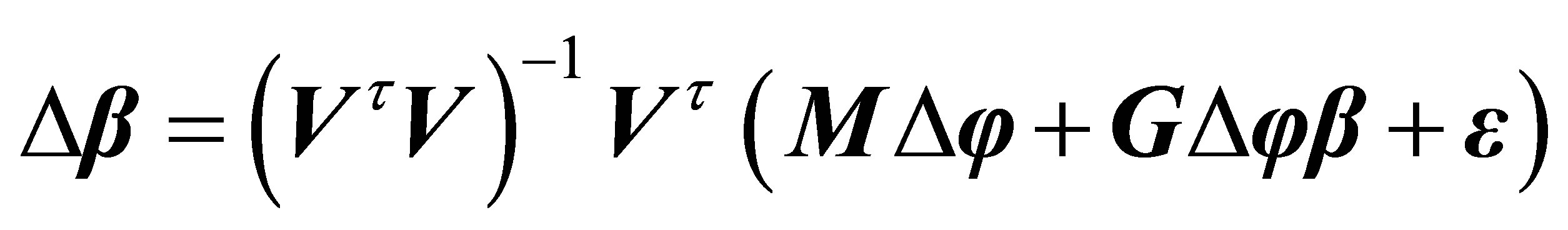
Equation (16) illustrates that the estimation error 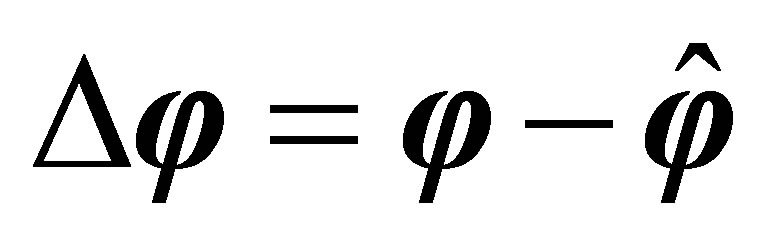 of
of  and
and ![]() impose “approximately” linear influences on the estimation error
impose “approximately” linear influences on the estimation error 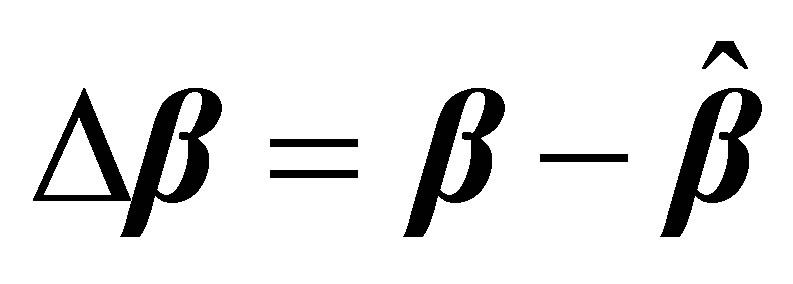 of
of![]() , and it is “approximately” because
, and it is “approximately” because  includes
includes .
.
4. Simulation
We take the sample points at 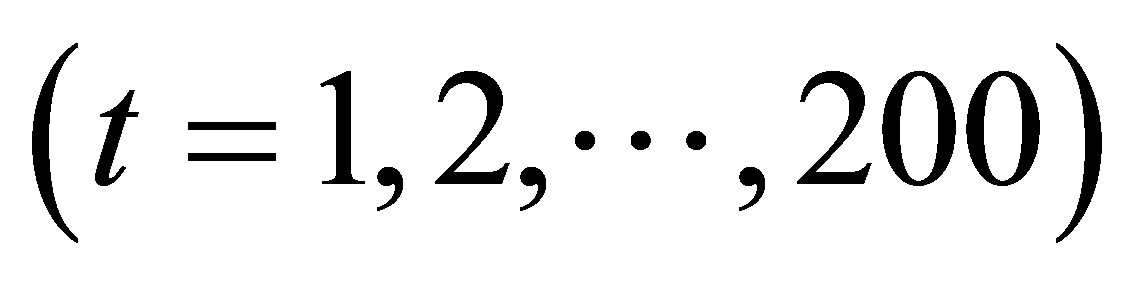 and two simulation models.
and two simulation models.
Model I (trigonometric function signal):
 (17)
(17)
Model II (mixed signal):
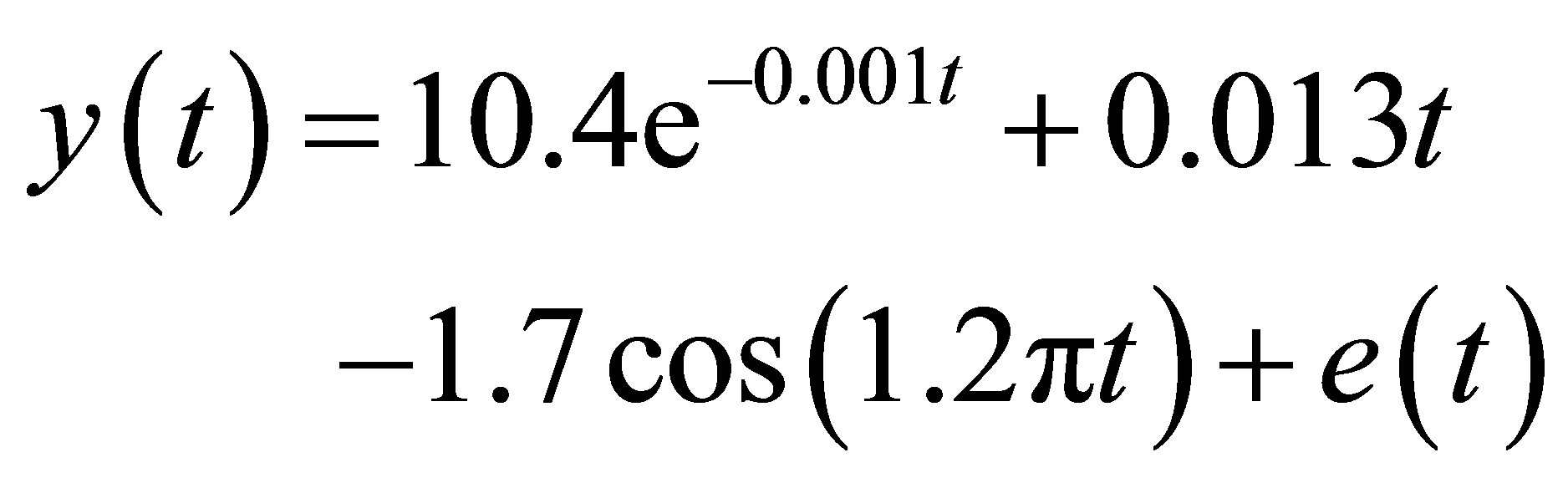 (18)
(18)
where the model of ![]() is an AR(4) model as
is an AR(4) model as
 (19)
(19)
Table 1 lists the estimation results of ![]() by using the method proposed in this paper and the least squares estimate (LSE) respectively. Table 2 illustrates the estimation results of
by using the method proposed in this paper and the least squares estimate (LSE) respectively. Table 2 illustrates the estimation results of  by using our method, and the least squares estimate of the AR parameters of Equation (19) when pure AR model is applied. Table 1 shows that the method proposed here can obtain a much better estimation of
by using our method, and the least squares estimate of the AR parameters of Equation (19) when pure AR model is applied. Table 1 shows that the method proposed here can obtain a much better estimation of ![]() than by using LSE. The results in Table 2 give a demonstration that the estimates of
than by using LSE. The results in Table 2 give a demonstration that the estimates of  by our methods are close to the LSE of
by our methods are close to the LSE of  in pure AR models. In summary, the method proposed in this paper is satisfactory.
in pure AR models. In summary, the method proposed in this paper is satisfactory.
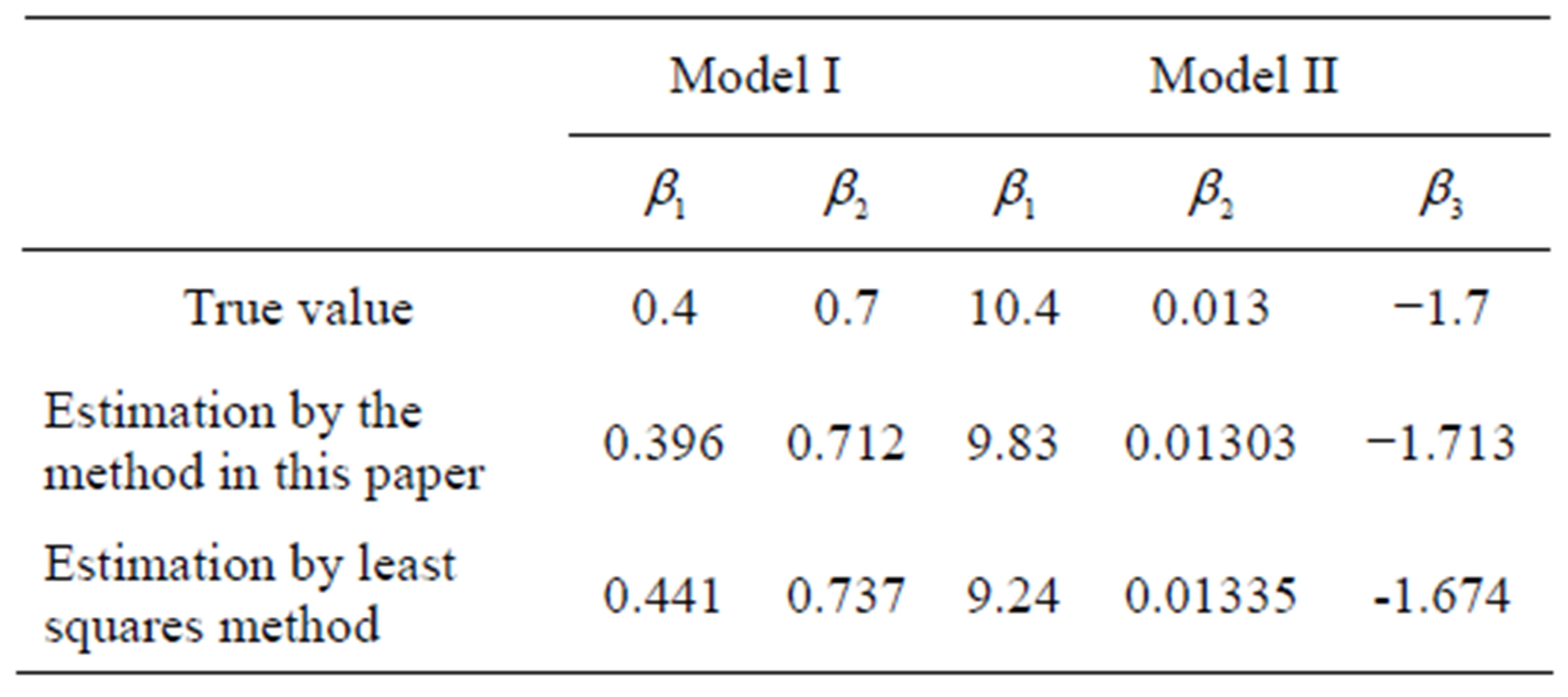
Table 1. The estimation of![]() .
.
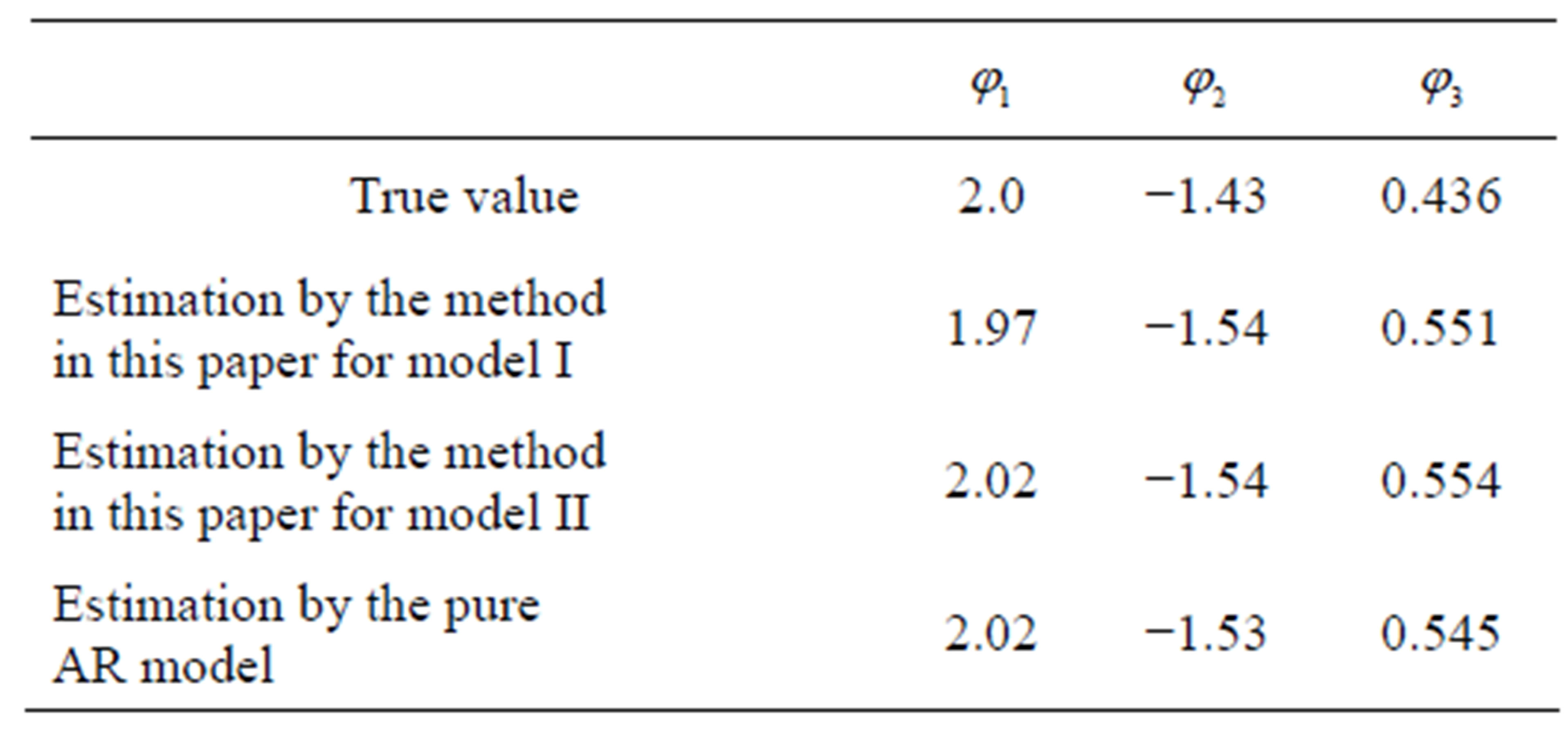
Table 2. The estimation of .
.
5. Conclusion
In this paper, a class of combined signal with AR noise is studied. The signal possesses the property of remaining form-invariant under the autoregressive operator. We proposed a parameter separation and two-step least squares method to separate the noise and signal and to give good estimates of each parameter. This method overcomes the difficulty with the conventional method for which the AR noise is unknown. It makes it easier to extract and estimate the true signal. It can provide good estimation effects for a wide class of signals and can be applied to the practical data analysis.
6. Acknowledgements
The authors thank the referees and the editors for their valuable comments on this paper.
REFERENCES
- H. H. Kelejian and I. R. Prucha, “A Generalized Moments Estimator for the Autoregressive Parameter in a Spatial Model,” International Economic Review, Vol. 40, No. 2, 1999, pp. 509-533. http://dx.doi.org/10.1111/1468-2354.00027
- S. Korl, H.-A. Loeliger and A. G. Lindgren, “AR Model Parameter Estimation: From Factor Graphs to Algorithms,” IEEE International Conference on Acoustics, Speech, and Signal Processing, Montreal, 17-21 May 2004, pp. 509-512.
- W.-K. Wong and G. R. Bian, “Estimating Parameters in Autoregressive Models with Asymmetric Innovations,” Statistics and Probability Letters, Vol. 71, No. 1, 2005, pp. 61-70. http://dx.doi.org/10.1016/j.spl.2004.10.022
- J. F. Liu and Z. L. Deng, “Self-Tuning Weighted Measurement Fusion Kalman Filter for ARMA Signals with Colored Noise,” Applied Mathematics & Information Sciences, Vol. 6, No. 1, 2012, pp. 1-7.
- M. Samonas and M. Petrou, “A Peak Preserving Algorithm for the Removal of Colored Noise from Signals,” IEEE Transactions on Signal Processing, Vol. 50, No. 11, 2002, pp. 2683-2694. http://dx.doi.org/10.1109/TSP.2002.804090
- D. Kozel and C. Apostoaia, “Colored Noise Reduction Using Bark Scale Spectral Subtraction, Statistics, and Multiple Time Frames,” IEEE International Conference on, Chicago, 17-20 May 2007, pp. 416-421.
- J. H. Jensen, M. G. Christensen and S. H. Jensen, “An Amplitude and Covariance Matrix Estimator for Signals in Colored Gaussian Noise,” 17th European Signal Processing Conference (EUSIPCO 2009), Glasgow, 24-28 August 2009, pp. 2485-2488.
NOTES
*Corresponding author.

