ABSTRACT

In this paper, we use Monte Carlo simulations to compare parametric estimators of Type 1 Tobit model. In particular, we examine the performance for finite samples of three different estimators of simple Tobit model: the least squares (LS) estimator, the Heckman (H) estimator and the maximum likelihood (ML) estimator. These three estimators are consistent and asymptotically normal in the case where the density error is specified. However, these properties are sensitive to the situation where the error distribution is not specified. The purpose of this article is to determine properties of the three estimators, namely bias and convergence, by using Monte Carlo simulations.

1. Introduction

The founder of Tobit models is James Tobin [1]. In this paper, he analyzed household expenditure on durable goods using a regression model which specifically took account of the fact that the expenditure (the dependent variable of his regression model) cannot be negative. Tobin called his model the model of limited dependent variables. It and its various generalizations are known popularly among economists as Tobit models, a phrase coined by Goldberger [2] because of similarities to probit models. These models are also known as censored or truncated regression models. The model is called truncated if the observations outside a specified range are totally lost, and censored if one can at least observe the exogenous variables. Censored and truncated regression models have been developed in other disciplines (notably biometrics and engineering) more or less independently of their development in econometrics. Biometricians use the model to analyze the survival time of a patient.

Amemiya [3] identified five kinds of Tobit models, the Tobit model is simply called Type 1 Tobit model, his fundamental paper on the censored normal regression model was the first systematic application in econometrics of the uniform law of large numbers and the central limit theorems required to establish consistency and asymptotic normality of nonlinear econometric models. The Tobit model is used when one is faced with many of observations for which the value of the endogenous variable is zero. This model implies that the observed value of the dependent variable is censored at zero.

In this paper, we use Monte Carlo simulations to compare parametric estimators of Type 1 Tobit model that of the theoretical part was studied by Amemiya [4].

In particular, we examine the performance for finite samples of three different estimators of simple Tobit model: the LS estimator, the H estimator and the ML estimator.

The purpose of this article is to determine properties of the three estimators, namely bias and convergence, by using Monte Carlo simulations.

The paper is organized as follows:

In the second section, we discus about parametric estimation of three different estimators simple Tobit model: the least squares estimator, the Heckman estimator and the maximum likelhood estimator. In the third section, we use Monte Carlo simulations to compare parametric estimators of Type 1 Tobit model and we finish our paper with some conclusions.

2. Parametric Estimation

This section presents parametric estimators of Type 1 Tobit model: the least squares estimator, the Heckman estimator and the maximum likelhood estimator.

A simple Tobit model (Type 1) is defined by the following equation:

(1)

where

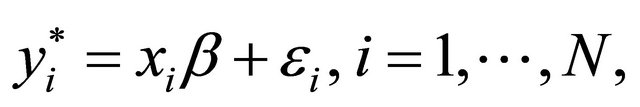
with y_i is the observed variable associated with the latent variable, , 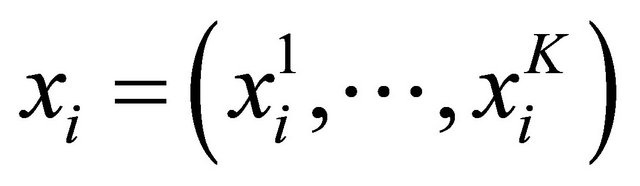is a vector of observable variables, is the vector of unknown parameters and is the errors which are independent and identically distributed according to a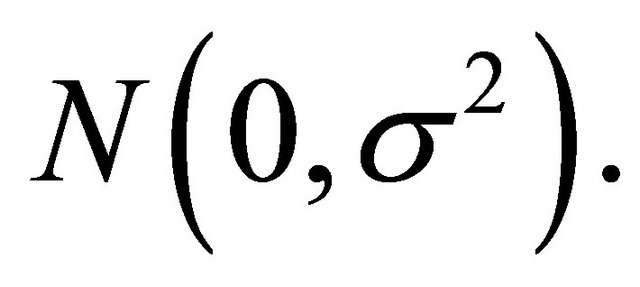

2.1. Least Squares Estimator

2.1.1. First Situation: The Exogenous Variables (x_i) Are Deterministic

The LS estimator, applied to all N pairs of observations, is defined by:

In this case, the LS estimator is inconsistent [4] and it is relatively difficult to give a general result on the form of bias of this estimator.

2.1.2. Second Situation: x_i Are Random Variables

Deal with this situation for which the exogenous variables x_i are random, Goldberger [5] studied this case by introducing a constant in the regression model. He wrote the model in the form:

(2)

with

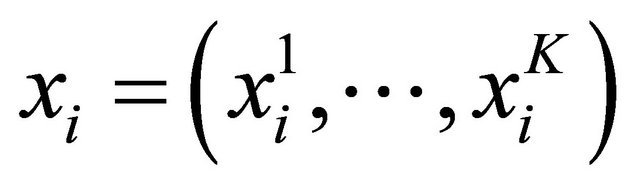is a vector of random normal distribution 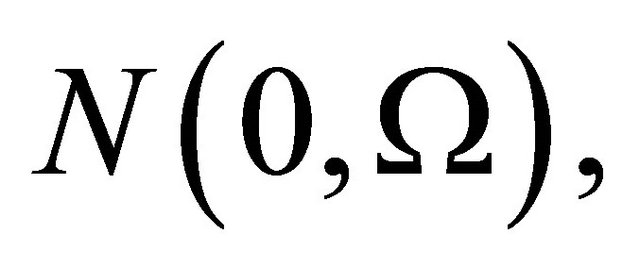where is defined positive matrix and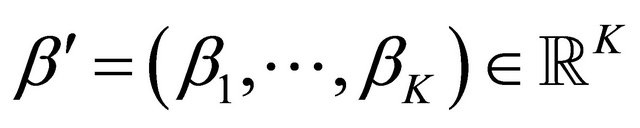, are the unknown parameters.

Fundamental assumption (FH)

We assume that the variables are distributed according to a normal with

Proposition 2.1 [Greene [6]]

Under the assumption (FH), the LS estimator, obtained on all observations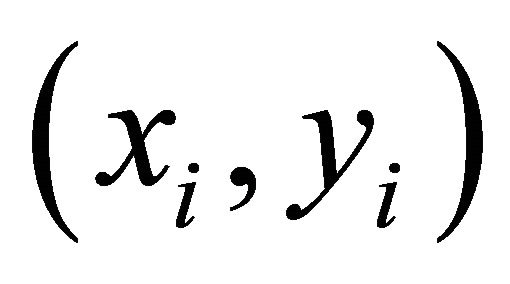, satisfies

where

Under the assumption (FH), the estimator defined by

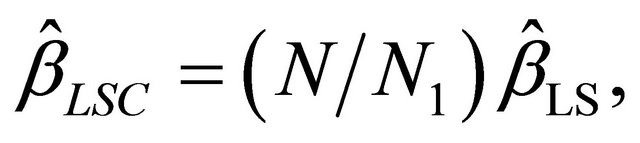
where is the number of observations for which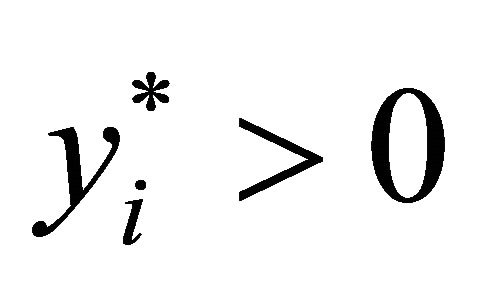, is a consistent estimator of:

.

2.2. Heckman’s Two-Step Estimator

The estimation procedure of Heckman [7] involves two steps.

Step 1: Estimate the ratio 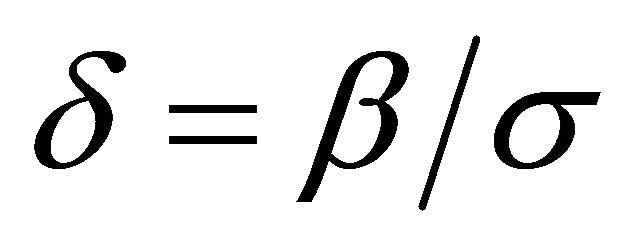from the following probit model by a method of maximum likelihood:

(3)

with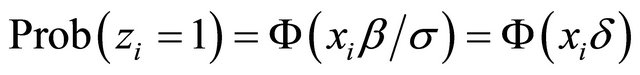, where is the standard normal distribution .

Step 2: Let the Maximum likelihood estimator of.

Regress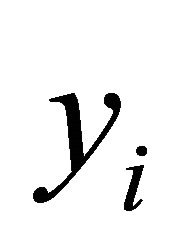, on and by least squares method’s using only the positive observations on: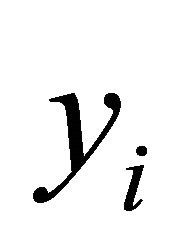

where is the ratio of mild defined by

where and are the distribution and density function respectively of the standard normal variable and. There the estimator of the Tobit model parameter is:

Proposition 2.2 (Heckman [7]) Heckman’s two-step estimator of is consistent.

2.3. Maximum Likelihood Estimator

In 70 years, the estimation procedure in two steps of Heckman and other methods of estimation were preferred because they do not require too much calculation. Today with the development of computer that can treat quickly the optimization problems of functions, the maximum likelihood estimator is more favors. Using reparametrization of Olsen [8], the log-likelihood of a Tobit model is:

where N₁ is the number of observations for which y_i > 0. The LM estimator of 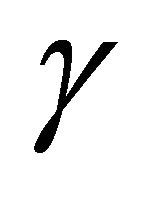is the solution of the problem:

Amemiya [4] proved that the maximum likelihood estimator and 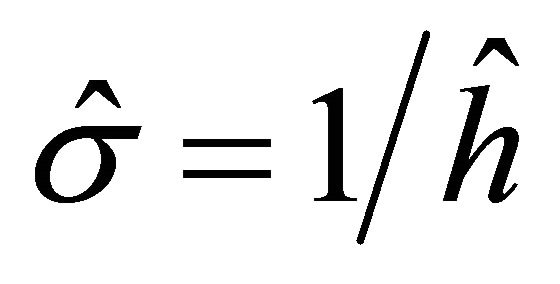are strongly consistent and asymptotically normal.

3. Simulation

We simulate in S-PLUS, 1000 replications of samples y of size N = 50, 100, 500, according to the following model:

(4)

where. Here, are distributed according to a normal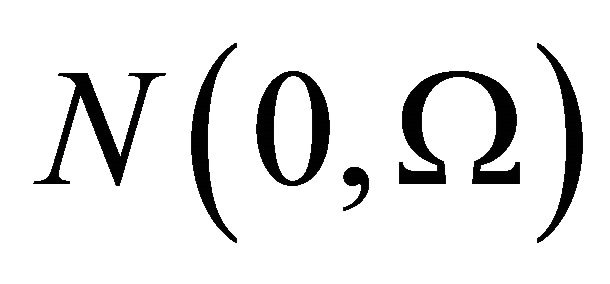, with varied distribution function: in the first case, in the second case follows from a logistic (0,1) distribution, and in the third case 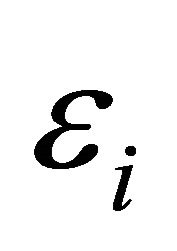follows from a uniform distribution (−2,2) and Cauchy distribution (0,1). For numerical values, we take, and.

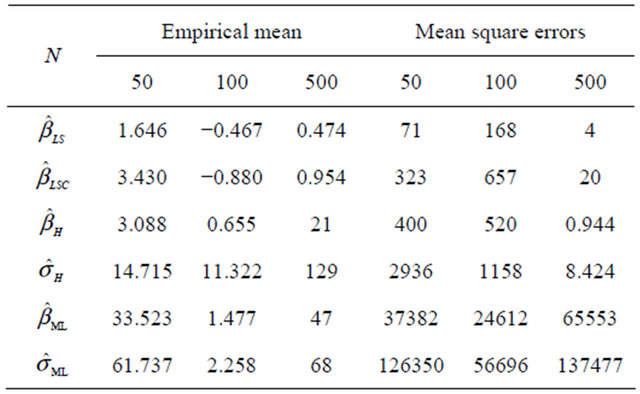
According to the simulation results, we can conclude that in the case where the errors follow from a normal distribution (Tables 1 and 2), the MSE tends to zero faster whenever sample size is greater. But in case where the errors follow from a Cauchy distribution (Table 3), the MSE does not tend to zero if the sample size is greater. The LS estimator is biased. Indeed the mean is of the order of 0.40. This confirms the result of Proposition which states that

.

For the empirical means and the mean square errors of LS estimator, Heckman and maximum likelihood estimators in the case of normal distribution (Table 1) error, the numerical results show that the maximum likelihood estimator and the Heckman estimator are on average quite close to the estimated values. Moreover, their mean square errors tend to zero faster than those of least squares estimators corrected. In conclusion, we can say that to estimate the parameters of the Tobit model, methods of maximum likelihood and Heckman are more effective than least squares estimator. But in the case when the error distribution is non-normal (Tables 2 and 3), the simulations show that the three estimators are not converging.

4. Conclusions

We have investigated and compared the finite sample performances of the three different parametric estimators

Table 1. The empirical means and the mean square errors (MSE) of estimators, of OLS, Heckman and maximum likelihood with normal error distribution.

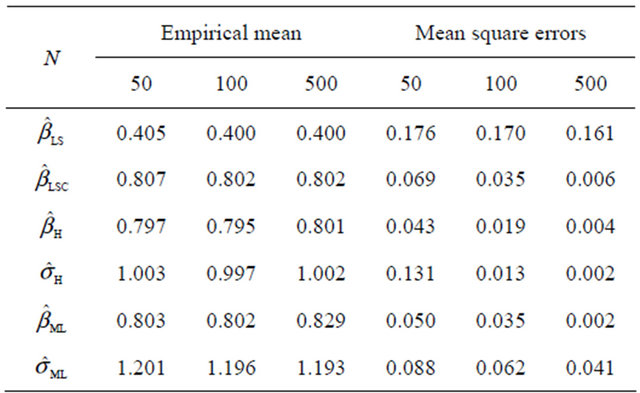
Table 2. The empirical means and the mean square errors of estimators, of OLS, Heckman and maximum likelihood with the logistic error distribution.

Table 3. The empirical means and the mean square errors of estimators, of OLS, Heckman and maximum likelihood with the uniform + Cauchy error distribution.

for a Type 1 Tobit model.

In general, the Monte Carlo simulation results indicate that all the parametric methods lead to similar result that the three different parametric estimators are converging if the density of errors is normal. However, these property is sensitive in the situation in which the error distribution is not normal. Our simulations reinforce the fact that parametric estimators of Type 1 Tobit models can be widely employed in empirical research with the standard assumption of normal error distributions.

REFERENCES