Open Journal of Statistics
Vol.2 No.1(2012), Article ID:17138,11 pages DOI:10.4236/ojs.2012.21001
An Approximate Hotelling T2-Test for Heteroscedastic One-Way MANOVA
Department of Statistics and Applied Probability, National University of Singapore, Singapore
Email: stazjt@nus.edu.sg
Received December 9, 2011; revised December 28, 2011; accepted January 11, 2012
Keywords: Approximate Hotelling T2 Test; Multivariate k-Sample Behrens-Fisher Problem; Wishart-Approximation; Wishart Mixture
ABSTRACT
In this paper, we consider the general linear hypothesis testing (GLHT) problem in heteroscedastic one-way MANOVA. The well-known Wald-type test statistic is used. Its null distribution is approximated by a Hotelling T2 distribution with one parameter estimated from the data, resulting in the so-called approximate Hotelling T2 (AHT) test. The AHT test is shown to be invariant under affine transformation, different choices of the contrast matrix specifying the same hypothesis, and different labeling schemes of the mean vectors. The AHT test can be simply conducted using the usual F-distribution. Simulation studies and real data applications show that the AHT test substantially outperforms the test of [1] and is comparable to the parametric bootstrap (PB) test of [2] for the multivariate k-sample Behrens-Fisher problem which is a special case of the GLHT problem in heteroscedastic one-way MANOVA.
1. Introduction
The problem of comparing the mean vectors of k multivariate populations based on k independent samples is referred to as multivariate analysis of variance (MANOVA). If the k covariance matrices are assumed to be equal, Wilks’ likelihood ratio, Lawley-Hotelling trace, Bartlett-Nanda-Pillai’s trace and Roy’s largest root tests ([3], Ch. 8, Sec. 6) can be used. When k = 2, Hotelling’s T2 test is the uniformly most powerful affine invariant test. These tests, however, may become seriously biased when the assumption of equality of covariance matrices is violated. In real data analysis, such an assumption is often violated and is hard to check.
The problem for testing the difference between two normal mean vectors without assuming equality of covariance matrices is referred to as the multivariate Behrens-Fisher (BF) problem. This problem has been well addressed in the literature. Reference [4] essentially showed, via some intensive simulations, that when there is no information about the correctness of the assumption of the equality of the covariance matrices, it is better to directly proceed to make inference using some BF testing procedure which is robust against the violation of the assumption, e.g., using the modified Nel and van der Mere’s (MNV) test proposed by [5]. Other such testing procedures include those proposed by [1,6-11], among others. Reference [12] compared seven tests and recommended the tests of [8,9]. However, Reference [5] noted that both [8,9]’s tests are not affine invariant. Further studies by [5,10,11] indicate that the MNV test is comparable to, or better than, other affine invariant tests.
When k > 2, and the covariance matrices are unknown and arbitrary, the problem of testing equality of the mean vectors is more complex, and only approximate solutions are available. Some of these solutions are obtained via generalizing the associated solutions to the univariate BF problem. For example, Reference [6]’s first and second-order tests are extensions of his series solutions to the univariate BF problem. Reference [1] generalized [13]’s univariate approximate degrees of freedom solution to heteroscedastic one-way MANOVA. Both tests are based on an affine-invariant test statistic but used different approaches to approximate its null distribution. Reference [14] proposed a generalized F-test. Reference [15] compared James’s first and second-order tests, Johansen’s test, and Bartlett-Nanda-Pillai’s trace test and concluded that none of them is satisfactory for all sample sizes and parameter configurations. Overall, they recommended the James second-order test followed by the Johansen test. Reference [2] claimed, based on a preliminary study, that the James second-order test is computationally very involved, and is difficult to apply when k = 3 or more, and offered little improvement over the Johansen test. They then proposed a parametric bootstrap (PB) test to the multivariate k-sample BF problem or heteroscedastic one-way MANOVA, which is an extension of their test to the univariate k sample BF problem (see [16]). They compared their test, via some intensive simulations for various sample sizes and parameter configurations against the Johansen test and the generalized F-test of [14] and found that their PB test performed best, followed by the Johansen test while the generalized F-test performed worst.
In this paper, we consider the general linear hypothesis testing (GLHT) problem in heteroscedastic one-way MANOVA. The well-known Wald-type test statistic is used. Its null distribution is approximated by a Hotelling T2 distribution with one parameter estimated from the data, resulting in the so-called approximate Hotelling T2 (AHT) test. The AHT test can be regarded as a natural extension of [8]’s test and [5]’s MNV test from for the multivariate two-sample BF problem to for the GLHT problem in heteroscedastic one-way MANOVA. In view of the good performance of [8]’s test (see [12]), the MNV test (see [5]), and the AHT tests for one-way and two-way ANOVA (see [17,18]), we expect that the AHT test will also perform well for heteroscedastic one-way MANOVA. The AHT test is shown to be invariant under affine transformation, different choices of the contrast matrix used to specify the same hypothesis, and different labeling schemes of the mean vectors. It can be simply conducted using the usual F-distribution. Intensive simulations are conducted to compare the AHT test against the Johansen test and the PB test under various sample sizes and parameter configurations. The simulation results show that the AHT test indeed performs well and it outperforms the Johansen test substantially and is comparable to the PB test of [2].
The rest of the paper is organized as follows. In Section 2, the AHT test is developed. Simulation studies are presented in Section 3. An application to a real data set is given in Section 4. Technical proofs of the main results are outlined in Section 5.
2. Main Results
2.1. The Wald-Type Test Statistic
Given k independent normal samples
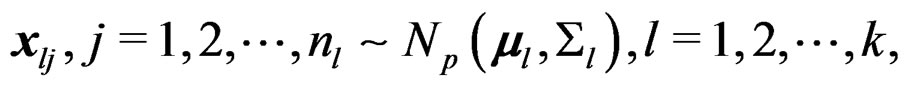 (1)
(1)
where and throughout,  denotes a p-dimensional normal distribution with mean vector
denotes a p-dimensional normal distribution with mean vector 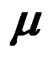 and covariance matrix V, we want to test whether the k mean vectors are equal:
and covariance matrix V, we want to test whether the k mean vectors are equal:
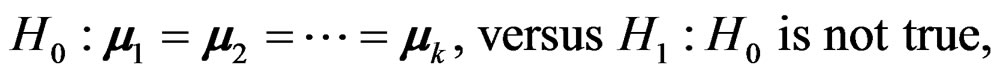 (2)
(2)
without assuming the equality of the covariance matrices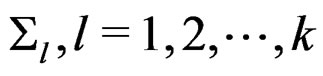 . The above problem is usually referred to as the multivariate k-sample BF problem or the overall heteroscedastic one-way MANOVA test, which is a special case of the following GLHT problem in heteroscedastic one-way MANOVA:
. The above problem is usually referred to as the multivariate k-sample BF problem or the overall heteroscedastic one-way MANOVA test, which is a special case of the following GLHT problem in heteroscedastic one-way MANOVA:
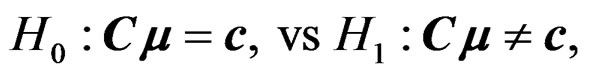 (3)
(3)
where 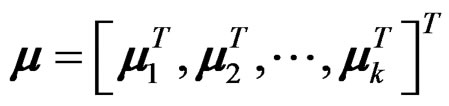 is a long mean vector obtained via stacking all the population mean vectors of the k samples together into a single column vector,
is a long mean vector obtained via stacking all the population mean vectors of the k samples together into a single column vector, 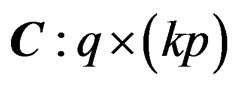 is a known coefficient matrix with Rank
is a known coefficient matrix with Rank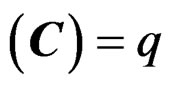 , and
, and  is a known constant vector. In fact, the GLHT problem (3) reduces to the multivariate k-sample BF problem (2) when we set
is a known constant vector. In fact, the GLHT problem (3) reduces to the multivariate k-sample BF problem (2) when we set 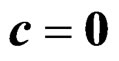 and set
and set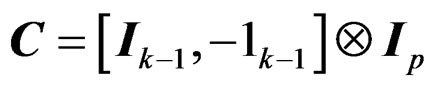 , a contrast matrix whose rows sum up to 0, where
, a contrast matrix whose rows sum up to 0, where 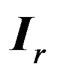 and
and 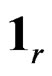 denote the identity matrix of size
denote the identity matrix of size 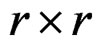 and a r-dimensional vector of ones, and
and a r-dimensional vector of ones, and  is the usual Kronecker product operator.
is the usual Kronecker product operator.
Remark 1 The contrast matrix C for the null hypothesis in (2) is not unique. For example, 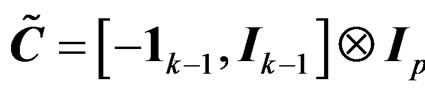 is also a contrast matrix for the null hypothesis in (2). However, it will be showed that the AHT test proposed in this paper will not depend on the choice of the contrast matrices specifying the same hypothesis.
is also a contrast matrix for the null hypothesis in (2). However, it will be showed that the AHT test proposed in this paper will not depend on the choice of the contrast matrices specifying the same hypothesis.
The GLHT problem (3) is very general. It includes not only the overall heteroscedastic one-way MANOVA test (2) but also various post hoc and contrast tests as special cases since any post hoc and contrast tests can be written in the form of (3). For example, when the overall heteroscedastic one-way MANOVA test is rejected, it is of interest to further test if  or if a contrast is zero, e.g.,
or if a contrast is zero, e.g., . In fact, these two testing problems can be written in the form of (3) with
. In fact, these two testing problems can be written in the form of (3) with 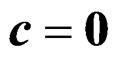 and
and
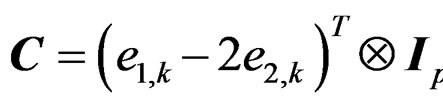 and
and 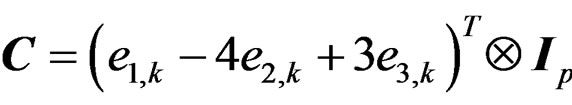
respectively where and throughout 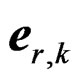 denotes a unit vector of length k with r-th entry being 1 and others 0.
denotes a unit vector of length k with r-th entry being 1 and others 0.
Remark 2 From the above various definitions of C, we have 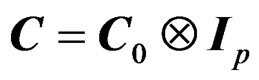 where
where 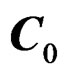 is a full rank matrix of size
is a full rank matrix of size 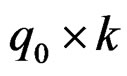 so that we always have
so that we always have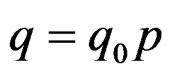 . If
. If 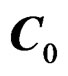 is a contrast matrix, so is C.
is a contrast matrix, so is C.
To construct the test statistic for the GLHT problem
(3), let 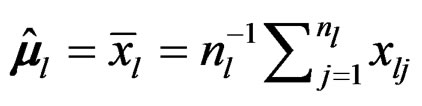 and
and
 be the sample mean vector and sample covariance matrix of the l-th sample. Set
be the sample mean vector and sample covariance matrix of the l-th sample. Set  which is an unbiased estimator of
which is an unbiased estimator of . Then
. Then 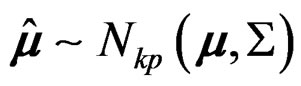 where
where
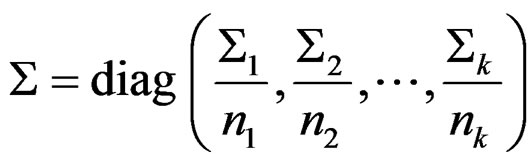 . It follows that
. It follows that
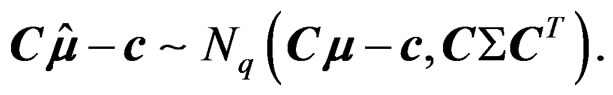 This suggests that a Wald-type test statistic can be constructed as
This suggests that a Wald-type test statistic can be constructed as
 (4)
(4)
where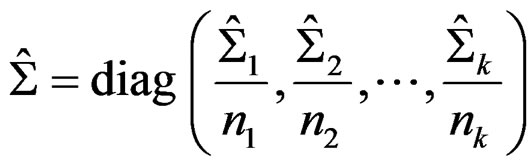 . Notice that the distribution of T is very complicated and its closed-form distribution is generally not tractable in the context of heteroscedastic one-way MANOVA.
. Notice that the distribution of T is very complicated and its closed-form distribution is generally not tractable in the context of heteroscedastic one-way MANOVA.
Remark 3 When the covariance matrix homogeneity is valid and the sample covariance matrices 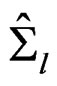 are replaced by their pooled sample covariance matrix
are replaced by their pooled sample covariance matrix 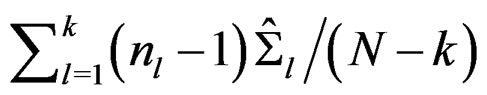 where
where  denotes the total sample size of the k samples, it is easy to show that
denotes the total sample size of the k samples, it is easy to show that 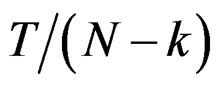 follows the distribution of the well-known Lawley-Hotelling trace test statistic ([3], Ch. 8, Sec. 6) with
follows the distribution of the well-known Lawley-Hotelling trace test statistic ([3], Ch. 8, Sec. 6) with 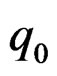 and
and  degrees of freedom where
degrees of freedom where 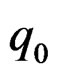 is defined in Remark 2.
is defined in Remark 2.
Remark 4 When the covariance matrix homogeneity is actually valid, we still can apply the AHT test proposed in this paper, pretending that the k sample covariance matrices 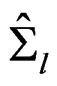 were not the same. We will see that the AHT test is simpler than the Lawley-Hotelling trace test which in general does not have a closed-form formula for its null distribution; see [3] (Ch. 8, Sec. 6). The simulation results presented in Section 3 show that the AHT test works reasonably well for those covariance matrix homogeneity cases.
were not the same. We will see that the AHT test is simpler than the Lawley-Hotelling trace test which in general does not have a closed-form formula for its null distribution; see [3] (Ch. 8, Sec. 6). The simulation results presented in Section 3 show that the AHT test works reasonably well for those covariance matrix homogeneity cases.
To construct the AHT test based on T, following [5] and [10], we re-express T as
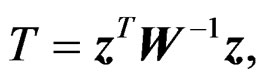 (5)
(5)
where 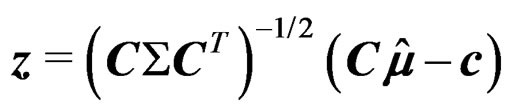 and
and
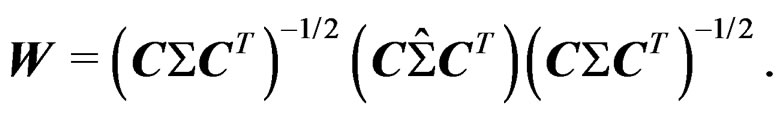 Notice that the above re-expression theoretically helps the development of the AHT test but in practice we still use (4) to compute the value of T. We have
Notice that the above re-expression theoretically helps the development of the AHT test but in practice we still use (4) to compute the value of T. We have 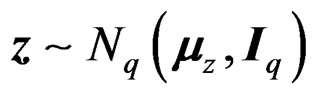 where
where
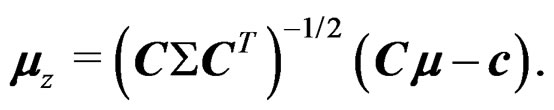 Let
Let 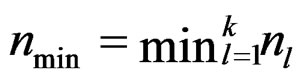 and
and
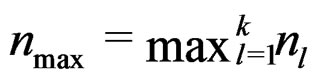 . Let
. Let 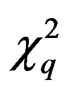 denote a
denote a 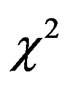 -distribution with q degrees of freedom.
-distribution with q degrees of freedom.
Remark 5 Assume that the sample sizes 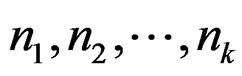 tend to infinity proportionally. That is,
tend to infinity proportionally. That is,
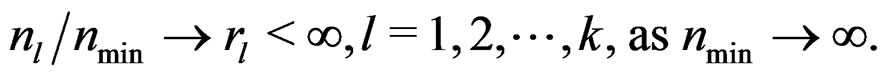 (6)
(6)
Then it is easy to show that as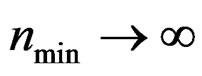 , T asymptotically follows
, T asymptotically follows . However, we can show that the convergence rate of T to
. However, we can show that the convergence rate of T to  is of order
is of order 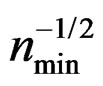 which is rather slow. Thus, the resulting
which is rather slow. Thus, the resulting 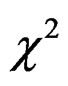 -test is hardly useful for the heteroscedastic GLHT problem (3).
-test is hardly useful for the heteroscedastic GLHT problem (3).
Remark 6 When the assumption (6) is not satisfied, the ratio 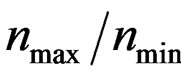 will tend to
will tend to 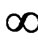 as
as 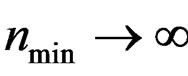 so that the limit of
so that the limit of  is not a full rank matrix and hence the limit of
is not a full rank matrix and hence the limit of 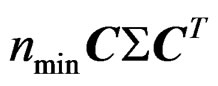 is not invertible. In this case, the test statistic T is not well defined so that the AHT test proposed in this paper will not perform well.
is not invertible. In this case, the test statistic T is not well defined so that the AHT test proposed in this paper will not perform well.
Let 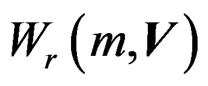 denote a Wishart distribution of m degrees of freedom and with covariance matrix
denote a Wishart distribution of m degrees of freedom and with covariance matrix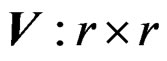 . We first show that W is a Wishart mixture, i.e., a linear combination of several independent Wishart random matrices. For this purpose, we decompose C into k blocks of size
. We first show that W is a Wishart mixture, i.e., a linear combination of several independent Wishart random matrices. For this purpose, we decompose C into k blocks of size 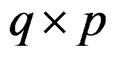 so that
so that 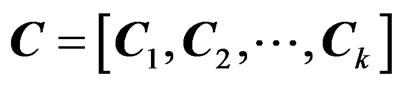 with
with  consisting of the first p columns of C,
consisting of the first p columns of C, 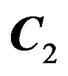 the second pcolumns of C, and so on.
the second pcolumns of C, and so on.
Remark 7 When 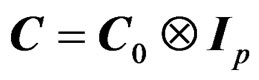 where
where 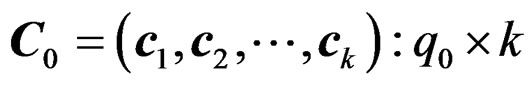 with
with 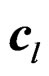 being the l-th column of
being the l-th column of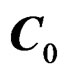 , we have
, we have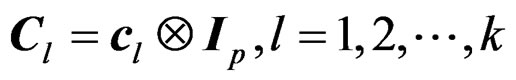 .
.
Set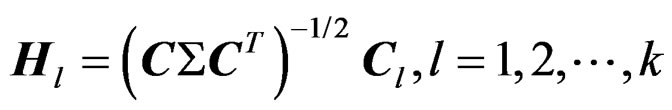 . Then
. Then
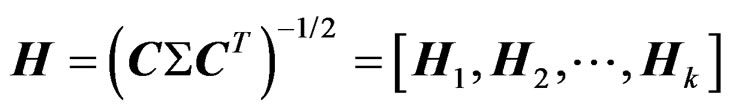 . Define the total variation of a random matrix
. Define the total variation of a random matrix 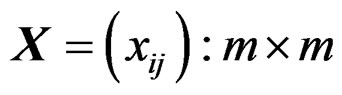 as
as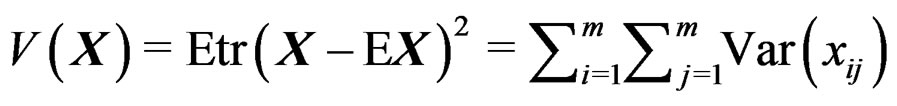 , i.e., the sum of the variances of all the entries of X.
, i.e., the sum of the variances of all the entries of X.
Theorem 1 We have
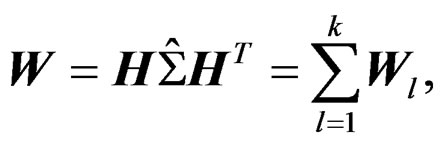 (7)
(7)
where 
are independent with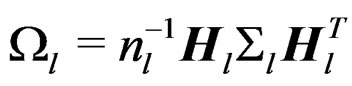 . Furthermore,
. Furthermore,
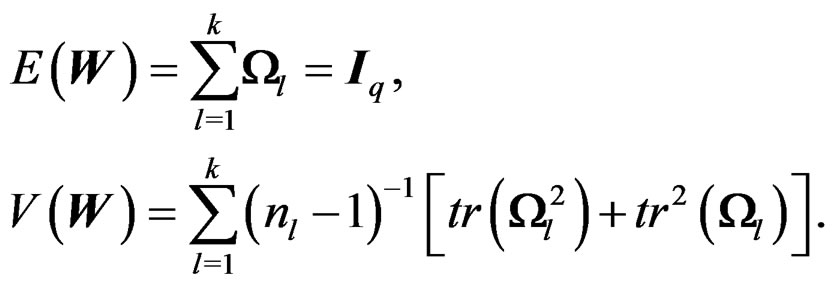 (8)
(8)
Theorem 1 is important for the AHT test. It says that W is a Wishart mixture and it gives the mean matrix and the total variation of W.
2.2. The AHT Test
When 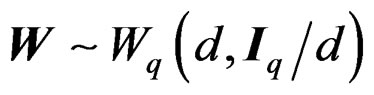 were valid with
were valid with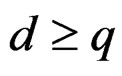 , the random variable T given in (5) would follow
, the random variable T given in (5) would follow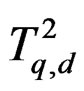 , a Hotelling T2-distribution with parameters q and d. Theorem 1 shows that W is in general a Wishart mixture instead of a single Wishart random matrix. To overcome this difficulty, we may approximate the distribution of W by that of a single Wishart random matrix, say,
, a Hotelling T2-distribution with parameters q and d. Theorem 1 shows that W is in general a Wishart mixture instead of a single Wishart random matrix. To overcome this difficulty, we may approximate the distribution of W by that of a single Wishart random matrix, say,  where the unknown parameters d and
where the unknown parameters d and  are determined via matching the mean matrices and total variations of W and R. That is, we solve the following two equations for d and
are determined via matching the mean matrices and total variations of W and R. That is, we solve the following two equations for d and :
:
 (9)
(9)
The solution is given in Theorem 2 below together with the range of d.
Theorem 2 The solution of (9) is given by
 (10)
(10)
Moreover, d satisfies the following inequalities:
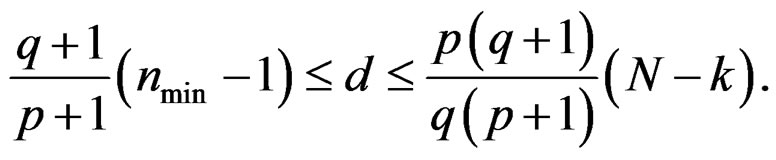 (11)
(11)
Remark 8 Theorem 2 indicates that 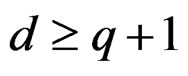 provided
provided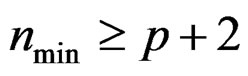 . This guarantees that the distribution of the test statistic T defined in (5) can be approximated by
. This guarantees that the distribution of the test statistic T defined in (5) can be approximated by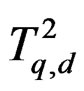 . That is why the test proposed here is called the AHT (approximate Hotelling T2) test.
. That is why the test proposed here is called the AHT (approximate Hotelling T2) test.
Remark 9 From (10), it is seen that when 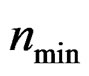 becomes large, d generally becomes large; and when
becomes large, d generally becomes large; and when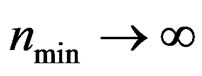 , we have
, we have 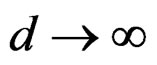 so that
so that 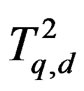 weakly tends to
weakly tends to , the limit distribution of T as pointed out in Remark 5.
, the limit distribution of T as pointed out in Remark 5.
Remark 10 The technique used to approximate a Wishart mixture W by a single Wishart random matrix  may be referred to as the Wishart-approximation method. The original version of the Wishartapproximation method is due to [8] who determined the unknown parameters d and
may be referred to as the Wishart-approximation method. The original version of the Wishartapproximation method is due to [8] who determined the unknown parameters d and  via matching the first two moments of W and R. The article obtained a number different solutions to d, with the simplest one being the same as the one presented in Theorem 2.
via matching the first two moments of W and R. The article obtained a number different solutions to d, with the simplest one being the same as the one presented in Theorem 2.
Remark 11 The key idea of the Wishart-approximation method is very similar to that of the well-known 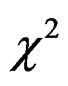 -approximation method developed by [19] who approximated the distribution of a
-approximation method developed by [19] who approximated the distribution of a 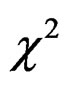 -mixture (see [20]) using that of a
-mixture (see [20]) using that of a 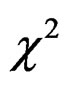 -random variable multiplied by a constant via matching the first two moments.
-random variable multiplied by a constant via matching the first two moments.
Remark 12 The first application of the Wishart-approximation method may be due to [8] who obtained an approximate test for the multivariate two-sample BF problem. The resulting test is not affine-invariant, as pointed out by [5]. The authors of [5] then modified Nel and van der Merwe’s test, resulting in the so-called MNV test. Recent applications of the Wishart-approximation method were given by [17,18] who studied tests of linear hypotheses in heteroscedastic one-way and two-way ANOVA. The AHT test proposed in this paper is a new application of the Wishart-approximation method.
In real data application, the parameter d has to be estimated based on the data. A natural estimator of d is obtained via replacing 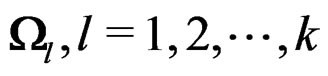 by their estimators:
by their estimators:
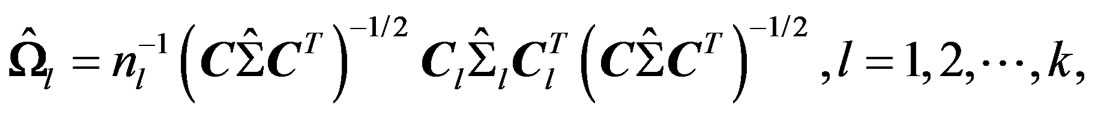 (12)
(12)
so that
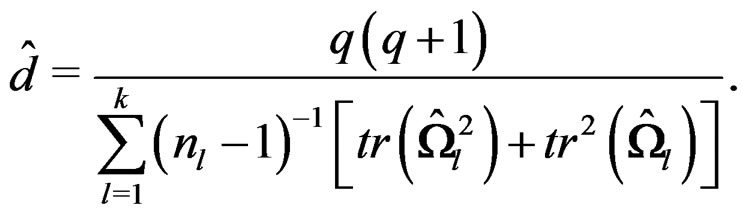 (13)
(13)
Notice that 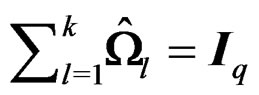 so that the range of d given in (11) is also the range of
so that the range of d given in (11) is also the range of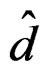 .
.
Remark 13 Under the assumption (6), it is standard to show that as , we have
, we have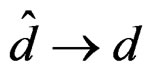 . In additionwe can show that
. In additionwe can show that 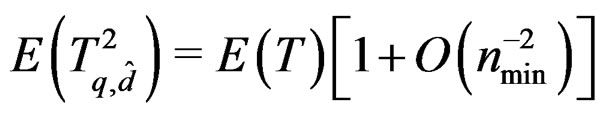 and
and 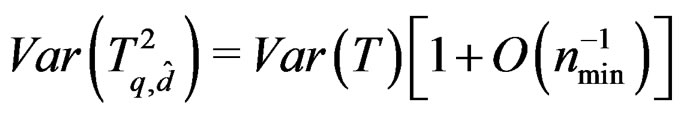 . That is, the means of T and
. That is, the means of T and  are matched up to order
are matched up to order 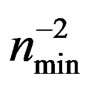 while the variances of T and
while the variances of T and 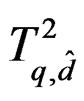 are matched only up to order
are matched only up to order . This is not bad since here we only use one tuning parameter
. This is not bad since here we only use one tuning parameter 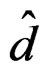 and the distribution of
and the distribution of 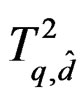 is easy to use.
is easy to use.
In summary, the AHT test is based on approximating the distribution of the Wald-type test statistic T (4) by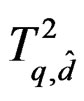 . It can be conducted using the usual F-distribution since
. It can be conducted using the usual F-distribution since
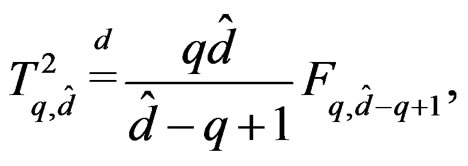 (14)
(14)
where and throughout, the expression  means “X and Y have the same distribution”. In other words, the critical value of the AHT test can be specified as
means “X and Y have the same distribution”. In other words, the critical value of the AHT test can be specified as
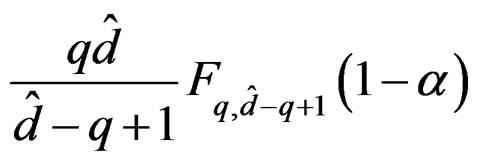 for the nominal significance level
for the nominal significance level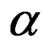 . We reject the null hypothesis in (3) when this critical value is exceeded by the observed test statistic T. The AHT test can also be conducted via computing the P-value based on the approximate distribution specified in (14).
. We reject the null hypothesis in (3) when this critical value is exceeded by the observed test statistic T. The AHT test can also be conducted via computing the P-value based on the approximate distribution specified in (14).
2.3. Minimum Sample Size Determination
Let 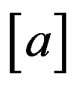 denote the integer part of a. When
denote the integer part of a. When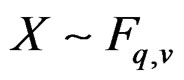 , it is easy to show that X has up to
, it is easy to show that X has up to 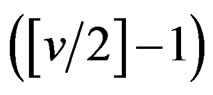 finite moments:
finite moments:

In general, T has some finite moments. If its approximate Hotelling T2-distribution 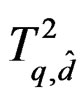 is good, it should also have the same number of finite moments. To assure that
is good, it should also have the same number of finite moments. To assure that 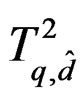 has up to r finite moments, by (14), the minimum sample size must satisfy
has up to r finite moments, by (14), the minimum sample size must satisfy
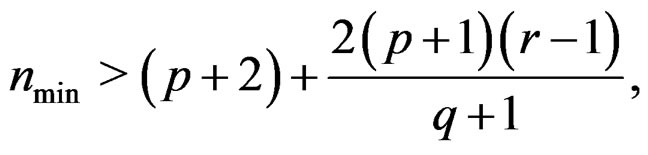 (15)
(15)
which is obtained via using the lower bound of d (and 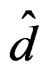 as well) given in (11). The required minimum sample size may be defined as
as well) given in (11). The required minimum sample size may be defined as 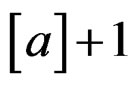 where a is the quantity given in the right-hand side of (15). It is seen that when p or r is large or when q is small, the required minimum sample size is also large. By Remark 2, we have
where a is the quantity given in the right-hand side of (15). It is seen that when p or r is large or when q is small, the required minimum sample size is also large. By Remark 2, we have 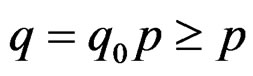 . Thus, a sufficient condition to guarantee that the approximate Hotelling T2-distribution
. Thus, a sufficient condition to guarantee that the approximate Hotelling T2-distribution 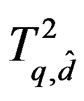 (14) has up to r finite moments is that
(14) has up to r finite moments is that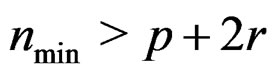 .
.
Remark 14 When 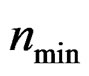 is too small, e.g.,
is too small, e.g., 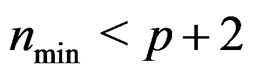 , the AHT test may not perform well since in this case, the first moment of
, the AHT test may not perform well since in this case, the first moment of 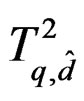 is not finite although the first moment of T is usually finite.
is not finite although the first moment of T is usually finite.
2.4. Properties of the AHT Test
In practice, the observed response vectors in (1) are often re-centered or rescaled before any inference is conducted. It is desirable that the inference is invariant under the recentering or rescale transformation. They are two special cases of the following affine transformation of the observed response vectors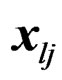 :
:
 (16)
(16)
where B is any nonsingular matrix and b is any constant vector. The proposed AHT test is affine-invariant as stated in the theorem below.
Theorem 3 The proposed AHT test is affine-invariant in the sense that both T and 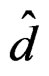 are invariant under the affine-transformation (16).
are invariant under the affine-transformation (16).
Remark 1 mentions that the contrast matrix C used to write (2) into the form of the GLHT problem (3) is not unique and the AHT test is invariant to various choices of the contrast matrix. This result follows from Theorem 4 below immediately if we notice a result from [21] (Ch. 5, Sec. 4), which states that for any two contrast matrices 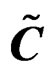 and C defining the same hypothesis, there is a nonsingular matrix P such that
and C defining the same hypothesis, there is a nonsingular matrix P such that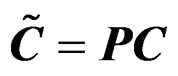 .
.
Theorem 4 The AHT test is invariant when the coefficient matrix C and the constant vector c in (3) are replaced with
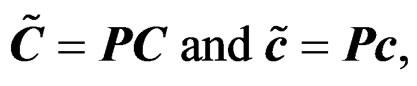 (17)
(17)
respectively where P is any nonsingular matrix.
Finally, we have the following result.
Theorem 5 The AHT test is invariant under different labeling schemes of the mean vectors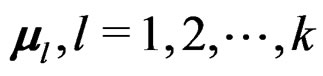 .
.
3. Simulation Studies
In this section, intensive simulations are conducted to compare the AHT test against the test of [1] and the PB test of [2]. All the three tests are affine-invariant. Reference [2] demonstrated that the PB test generally outperforms the test of [1] and the generalized F-test of [14] in terms of size controlling. The generalized F-test are generally very liberal and time consuming. Therefore, we shall not include it for comparison against the AHT test.
Following [2], for simplicity, we set 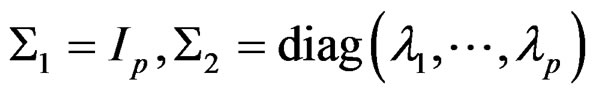 and
and 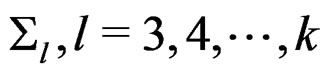 to be some positive definite matrices, where p,
to be some positive definite matrices, where p,  and other tuning parameters are specified later. Let
and other tuning parameters are specified later. Let 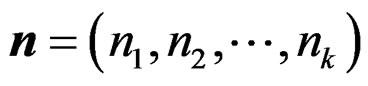 denote the vector consisting of the k sample sizes. For given n and
denote the vector consisting of the k sample sizes. For given n and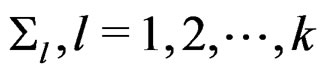 , we first generated k sample mean vectors
, we first generated k sample mean vectors 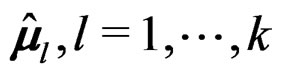 and k sample covariance matrices
and k sample covariance matrices 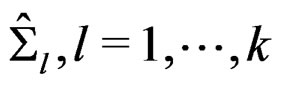 by
by
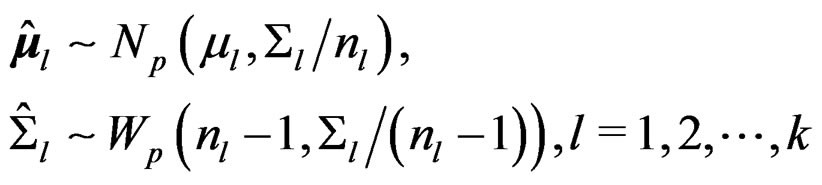
where the population mean vectors 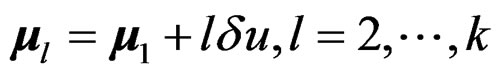 with
with 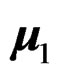 being the first population mean vector, u a constant unit vector specifying the direction of the population mean differences, and
being the first population mean vector, u a constant unit vector specifying the direction of the population mean differences, and 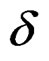 a tuning parameter controlling the amount of the population mean differences. Without loss of generality, we specified
a tuning parameter controlling the amount of the population mean differences. Without loss of generality, we specified 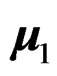 as 0 and u as
as 0 and u as 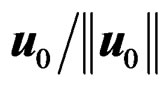 where
where 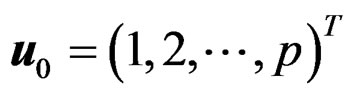 for any p and
for any p and 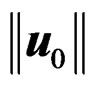 denotes the usual L2-norm of u0. We then applied the Johansen, PB, and AHT tests to the generated sample mean vectors and the sample covariance matrices, and recorded their P-values. The empirical sizes and powers of the Johansen, PB, and AHT tests were computed based on 10000 runs and the number of inner loops for the PB test is 1000. In all the simulations conducted, the significance level was specified as 5% for simplicity.
denotes the usual L2-norm of u0. We then applied the Johansen, PB, and AHT tests to the generated sample mean vectors and the sample covariance matrices, and recorded their P-values. The empirical sizes and powers of the Johansen, PB, and AHT tests were computed based on 10000 runs and the number of inner loops for the PB test is 1000. In all the simulations conducted, the significance level was specified as 5% for simplicity.
The empirical sizes (associated with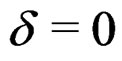 ) and powers (associated with
) and powers (associated with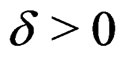 ) of the Johansen, PB, and AHT tests for the multivariate k-sample BF problem (2), together with the associated tuning parameters, are presented in Tables 1-3, in the columns labeled with “Joh”, “PB”, and “AHT” respectively. As seen from the three tables, three sets of the tuning parameters for population covariance matrices are examined, with the first set specifying the homogeneous cases and seven sets of sample sizes are specified, with the first three sets specifying the balanced sample size cases. To measure the overall performance of a test in terms of maintaining the nominal size
) of the Johansen, PB, and AHT tests for the multivariate k-sample BF problem (2), together with the associated tuning parameters, are presented in Tables 1-3, in the columns labeled with “Joh”, “PB”, and “AHT” respectively. As seen from the three tables, three sets of the tuning parameters for population covariance matrices are examined, with the first set specifying the homogeneous cases and seven sets of sample sizes are specified, with the first three sets specifying the balanced sample size cases. To measure the overall performance of a test in terms of maintaining the nominal size , we define the average relative error as
, we define the average relative error as  where
where 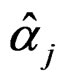 denotes the j-th empirical size for
denotes the j-th empirical size for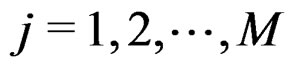 ,
, 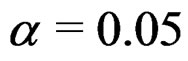 and M is the number of empirical sizes under consideration. The smaller ARE value indicates the better overall performance of the associated test. Usually, when ARE ≤ 10, the test performs very well; when
and M is the number of empirical sizes under consideration. The smaller ARE value indicates the better overall performance of the associated test. Usually, when ARE ≤ 10, the test performs very well; when , the test performs reasonably well; and when
, the test performs reasonably well; and when , the test does not perform well since its empirical sizes are either too liberal or too conservative. Notice that for a good test, the larger the sample sizes, the smaller the ARE values. Notice that for simplicity, in the specification of the covariance and sample size tuning parameters, we often use
, the test does not perform well since its empirical sizes are either too liberal or too conservative. Notice that for a good test, the larger the sample sizes, the smaller the ARE values. Notice that for simplicity, in the specification of the covariance and sample size tuning parameters, we often use  to denote “a repeats r times”, e.g., (30)2 = (30, 30) and (23, 4, 12) = (2, 2, 2, 4, 1, 1). Tables 1-3 show the empirical sizes and powers of the Johansen, PB, and AHT tests for a bivariate case with
to denote “a repeats r times”, e.g., (30)2 = (30, 30) and (23, 4, 12) = (2, 2, 2, 4, 1, 1). Tables 1-3 show the empirical sizes and powers of the Johansen, PB, and AHT tests for a bivariate case with , a
, a
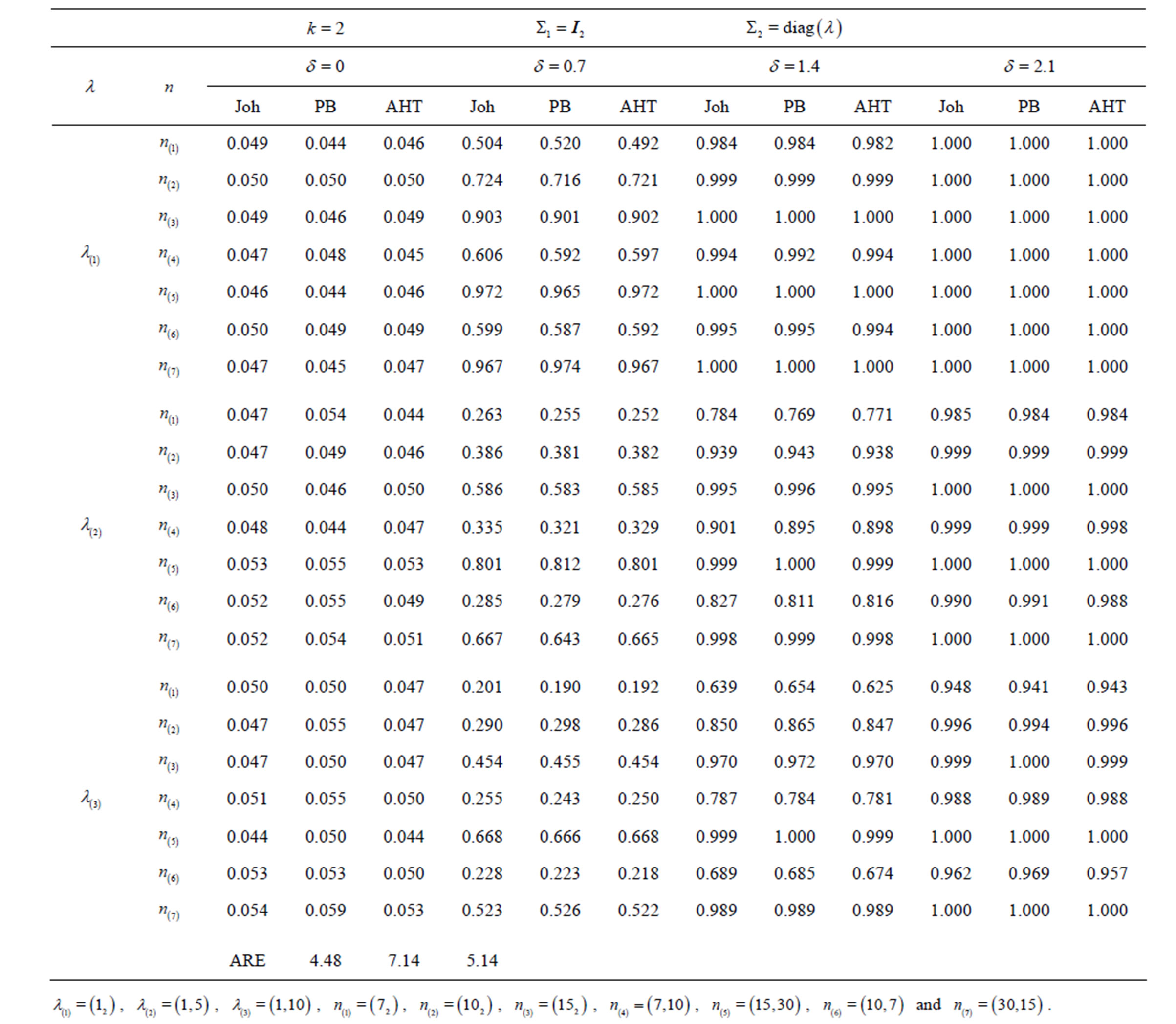
Table 1. Empirical sizes and powers of the Johansen, PB, and AHT tests for bivariate one-way MANOVA.
3-variate case with 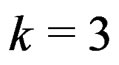 and a 5-variate case with
and a 5-variate case with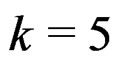 , respectively.
, respectively.
From Table 1, it is seen that for the two-sample BF problem, the Johansen, PB, and AHT tests performed very similarly with the Johansen test slightly outperforming the other two tests. However, from Tables 2 and 3, it is seen that with k increasing to 3 and 5, the Johansen test performed much worse than the PB and AHT tests. The later two tests were generally comparable for various sample sizes and parameter configurations. Since the PB test is much more computationally intensive, it is less attractive in real data analysis. The AHT test is then a nice alternative, especially when k is moderate or large.
4. Application to the Egyptian Skull Data
The Egyptian skull data set was recently analyzed by [2]. It can be downloaded freely at Statlib (http://lib.stat.cmu. edu/DASL/Stories/EgyptianSkullDevelopment.html).
There are five samples of 30 skulls from the early pre-dynastic period (circa 4000 BC), the late pre-dynastic period (circa 3300 BC), the 12-th and 13-th dynasties (circa 1850 BC), the Ptolemaic period (circa 200 BC), and the Roman period (circa AD 150). Four measurements are available on each skull, namely, 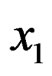 = maximum breadth,
= maximum breadth, 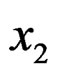 = borborygmatic height,
= borborygmatic height, 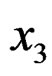 = dentoalveolar length, and
= dentoalveolar length, and  = nasal height (all in mm). To compare the AHT test with the test of [1] and the PB test of [2] in various cases, we applied these three tests to
= nasal height (all in mm). To compare the AHT test with the test of [1] and the PB test of [2] in various cases, we applied these three tests to
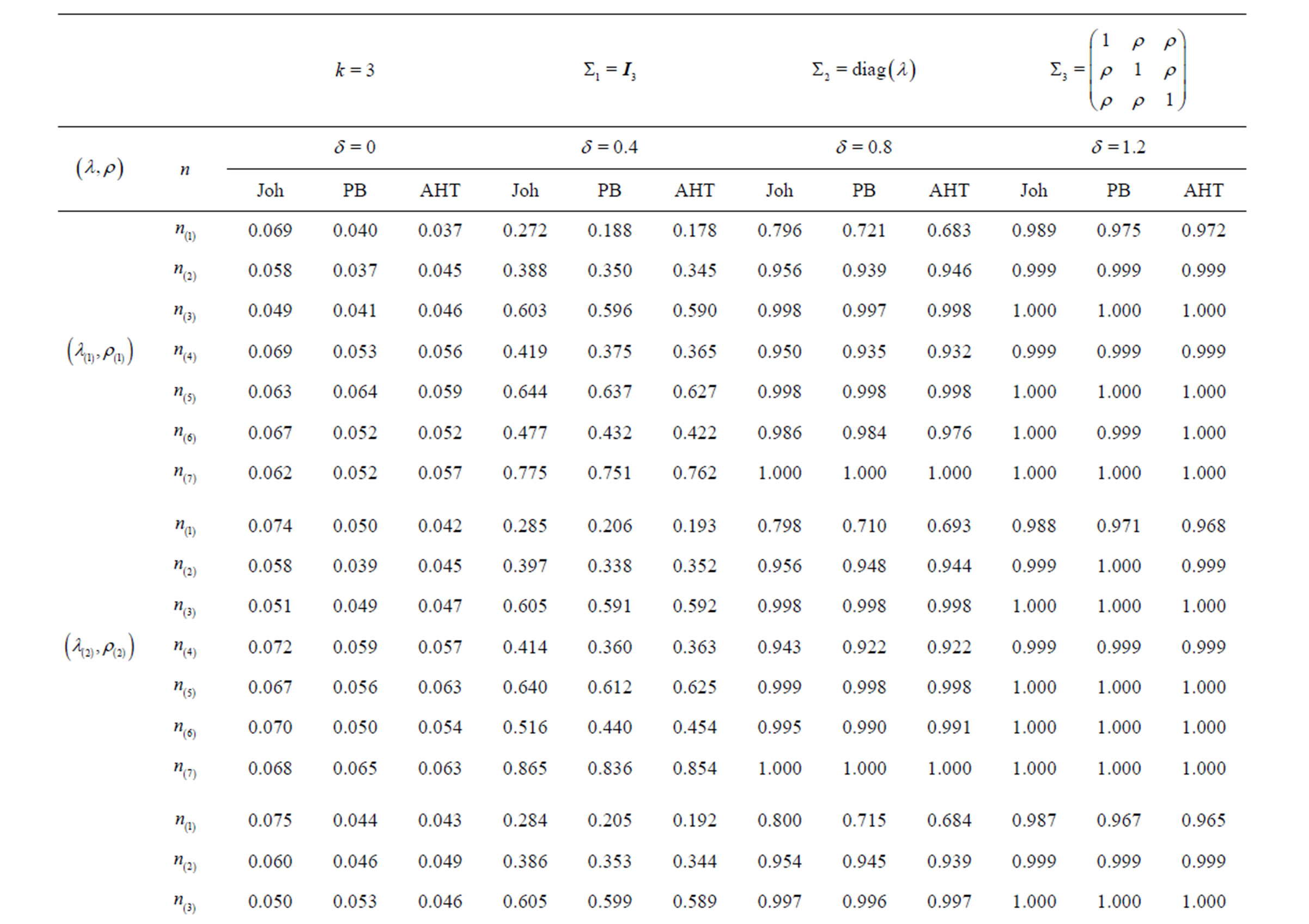

Table 2. Empirical sizes and powers of the Johansen, PB, and AHT tests for trivariate one-way MANOVA.
check the significance of the mean vector differences of the first k samples, using only the first  observations for
observations for 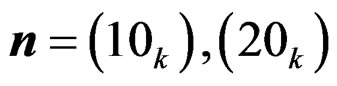 and
and 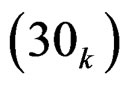 for k = 2, 3, 4 and 5. There are totally 12 cases under consideration. The number of bootstrap replications in the PB test is 10000 and hence the time spent by the PB test is about 10000 times of that spent by the other two tests. The P-values of the three tests for various cases are presented in Table 4.
for k = 2, 3, 4 and 5. There are totally 12 cases under consideration. The number of bootstrap replications in the PB test is 10000 and hence the time spent by the PB test is about 10000 times of that spent by the other two tests. The P-values of the three tests for various cases are presented in Table 4.
From Table 4, it is seen that the P-values of the three tests are close to each other with the P-values of the Johansen test slightly smaller in almost all the cases. Reference [2] showed via intensive simulations that the PB test performed well for various parameter configurations. Therefore, we may use the P-values of the PB test as benchmark to compare the AHT test with the Johansen test. It is seen from Table 4 that the P-values of the AHT tests are closer to the P-values of the PB test than those of the Johansen test. In this sense, the AHT test performed similar to the PB test and outperformed the Johansen test. This is in agreement with the conclusions drawn from the simulation results presented in the previous section.
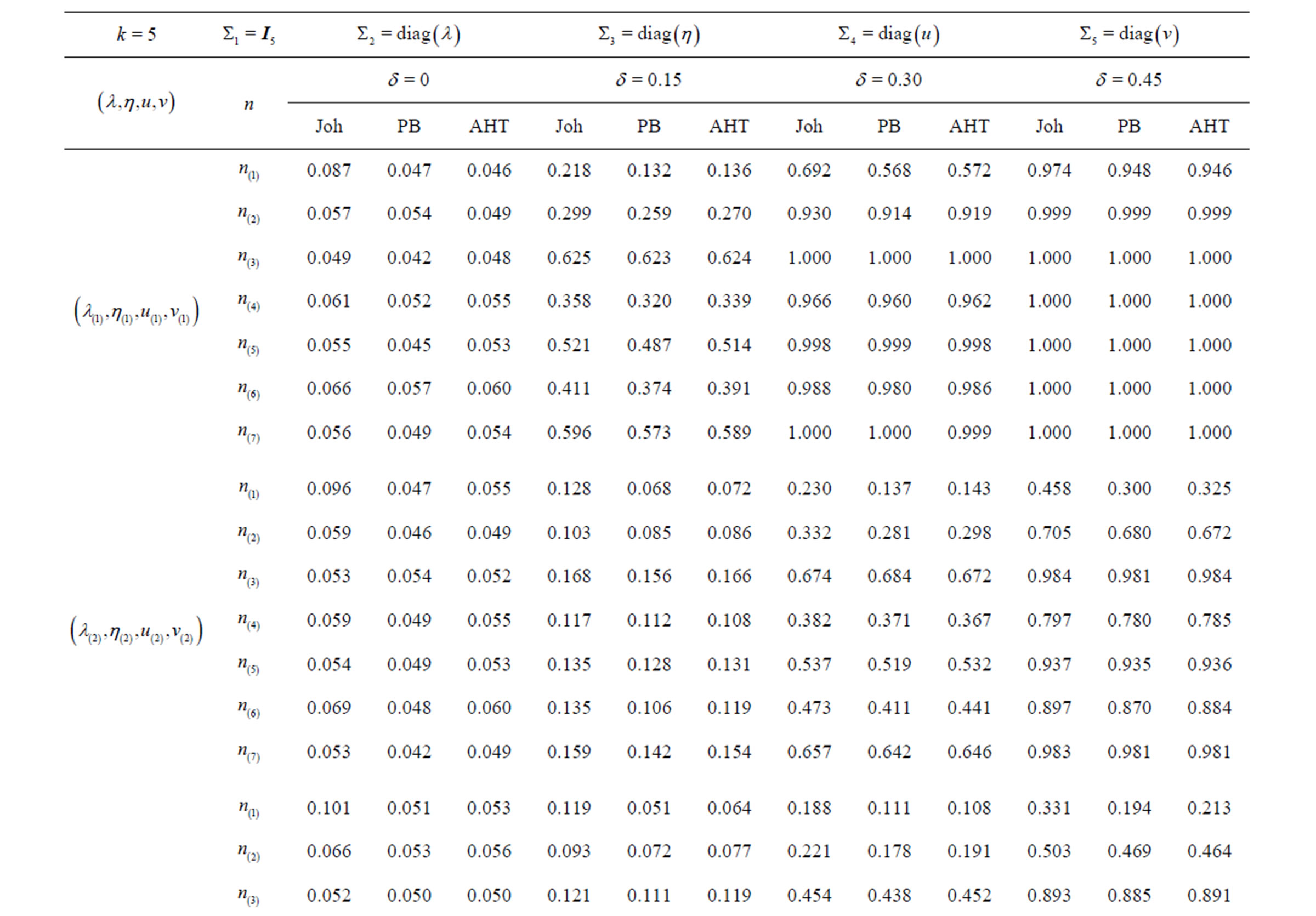

Table 3. Empirical sizes and powers of the Johansen, PB, and AHT tests for 5-variate one-way MANOVA.
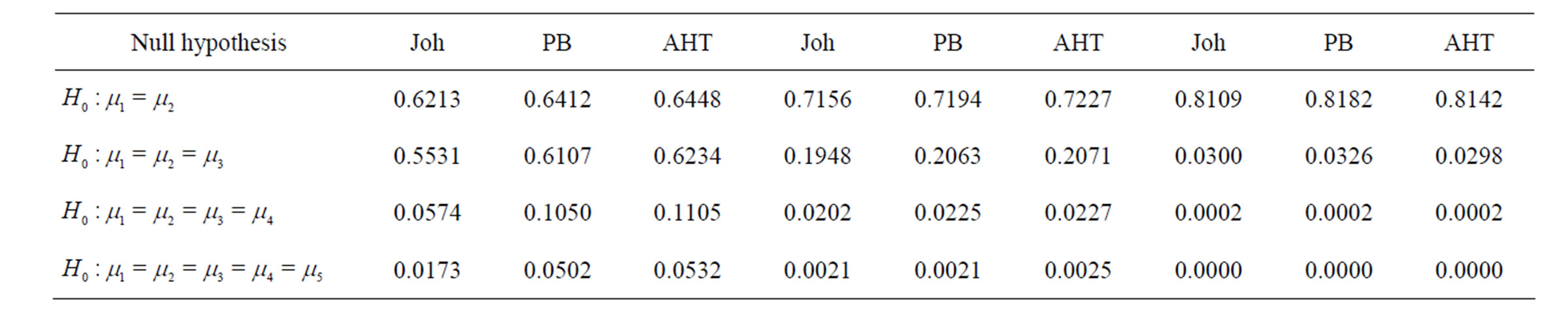
Table 4. P-values of the Johansen, PB, and AHT tests for the Egyptian skull data example.
It is also seen that the first null hypothesis in Table 4 is not significant, with the P-values of the three tests larger than 60% and increasing with increasing the sample sizes; the other three null hypotheses are significant, with the P-values of the three tests decreasing to less than 5% with increasing the sample sizes. These results suggest that the Egyptian skulls had little change in the early and late pre-dynastic periods but experienced a significant change over the later three periods.
5. Technical Proofs
Proof of Theorem 1 Notice first that if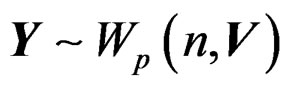 , then we have
, then we have  and
and
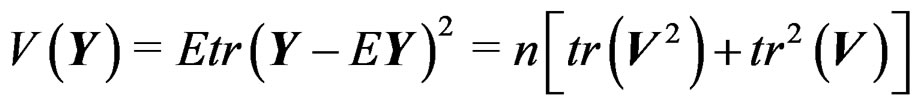 . In addition, it is well known that for
. In addition, it is well known that for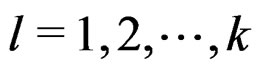 , we have
, we have
 . Thus
. Thus
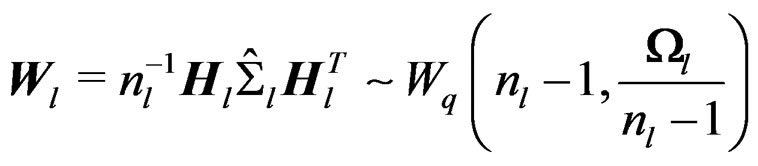
where
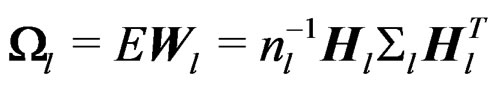 .
.
Therefore, we have 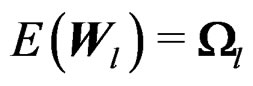 and
and
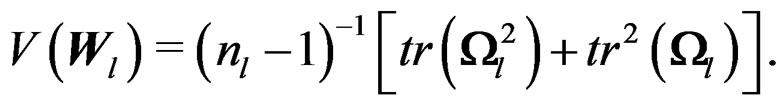
Since 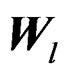 are independent, we have
are independent, we have
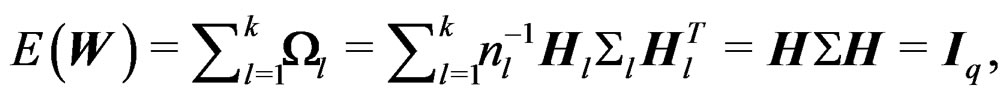
and
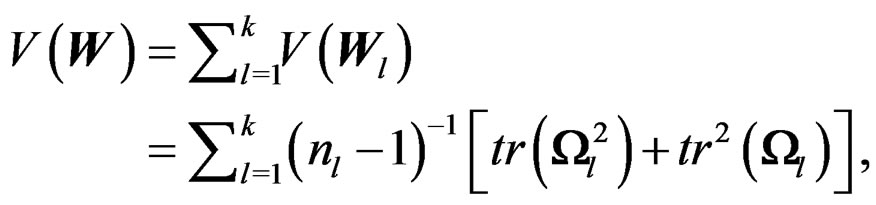
as desired. The theorem is proved.
Proof of Theorem 2 By Theorem 1, 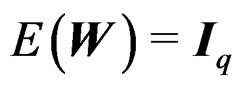 and
and
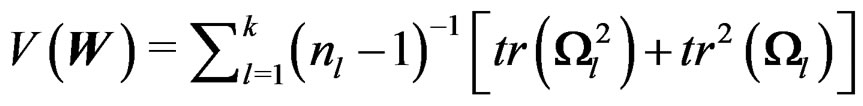 .
.
By the proof of Theorem 1, we have 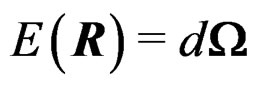 and
and
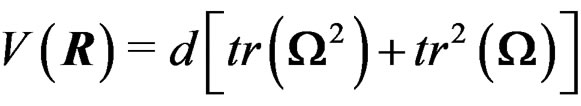 .
.
Equating 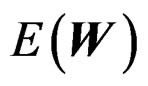 and
and 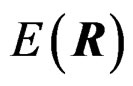 leads to
leads to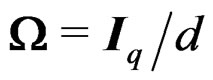 . It follows that
. It follows that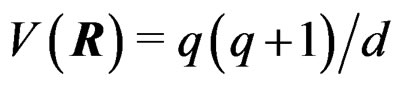 . Equating
. Equating  and
and 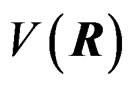 then leads to (10) as desired.
then leads to (10) as desired.
We first find the lower bound of d. This is equivalent to finding the upper bound of the denominator of d. For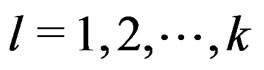 , set
, set 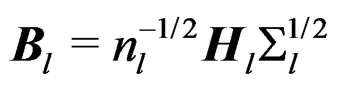 which is a
which is a 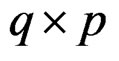 full rank matrix. Then
full rank matrix. Then . It follows that
. It follows that 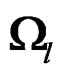 are nonnegative, so are their eigenvalues. In addition, the matrix
are nonnegative, so are their eigenvalues. In addition, the matrix 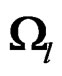 and the matrix
and the matrix 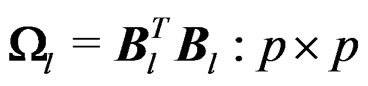 have the same non-zero eigenvalues. Thus,
have the same non-zero eigenvalues. Thus,  has at most p nonzero eigenvalues. Denote the largest p eigenvalues of
has at most p nonzero eigenvalues. Denote the largest p eigenvalues of 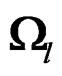 by
by  which include all the nonzero eigenvalues of
which include all the nonzero eigenvalues of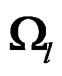 . By Theorem 1,
. By Theorem 1,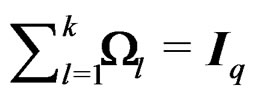 . This leads to
. This leads to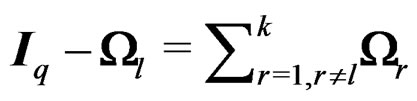 , which implies that
, which implies that 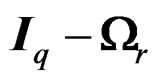 is nonnegative. By singular value decomposition of
is nonnegative. By singular value decomposition of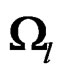 , it is easy to show that
, it is easy to show that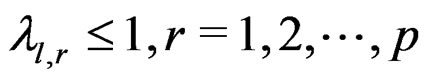 . It follows that
. It follows that
 and
and

Therefore,
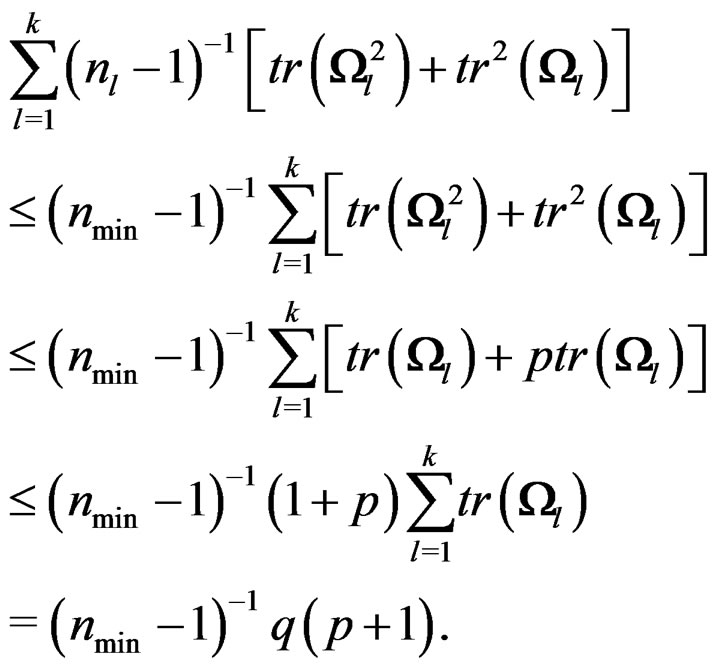
It follows that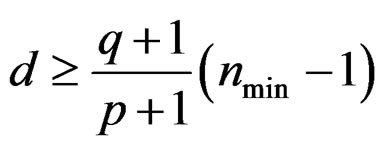 . The first inequality in (11) is proved.
. The first inequality in (11) is proved.
We now find the upper bound for d. This is equivalent to finding the minimum value of the denominator of d. Using the eigenvalues of 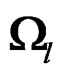 defined above, we have
defined above, we have
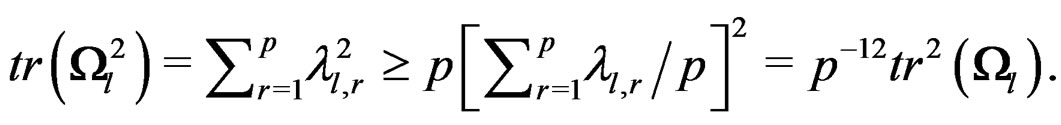
It follows that
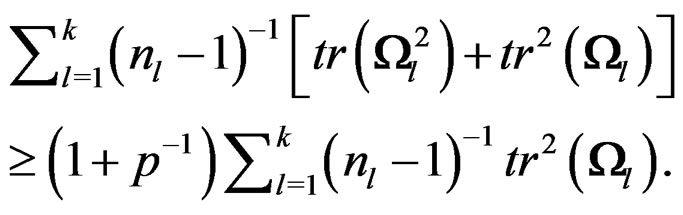
For convenience, we now set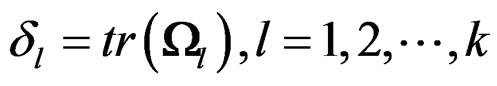 . Then by Theorem 1, we have
. Then by Theorem 1, we have 
Set 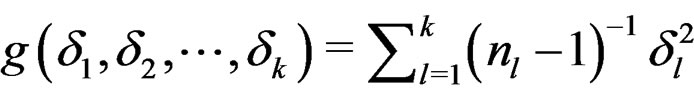 where
where 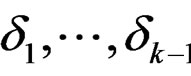
are linear independent but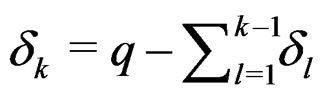 . Taking the partial derivatives of g with respect to
. Taking the partial derivatives of g with respect to 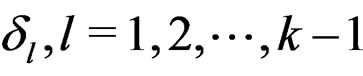 and setting them to 0 lead to the following normal equation system:
and setting them to 0 lead to the following normal equation system:
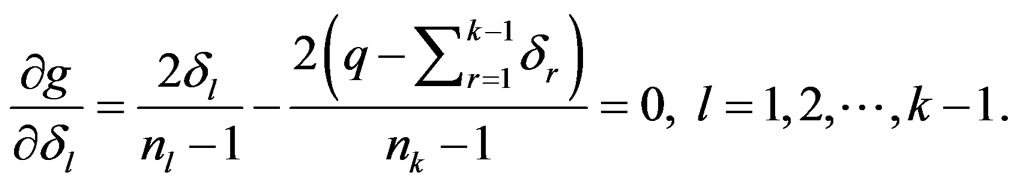
Solving the above equation system with respect to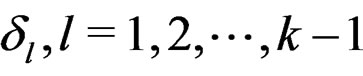 , together with the fact
, together with the fact , leads to
, leads to
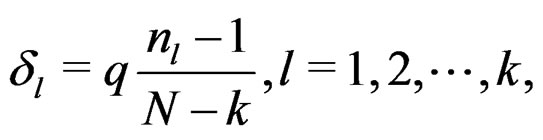 (18)
(18)
where 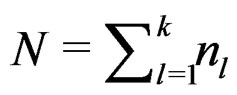 as defined before. Since for
as defined before. Since for 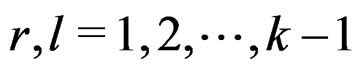 , we have
, we have
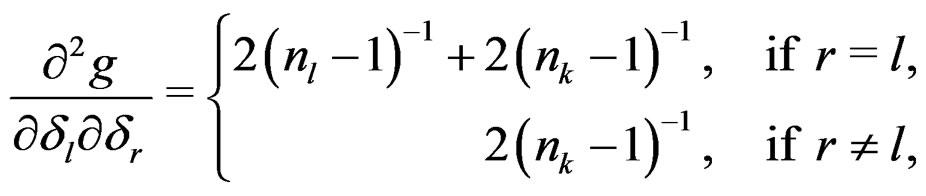
the associated Hessian matrix of g is positive definite. Thus, the function 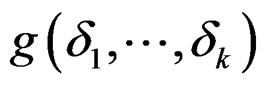 has minimum value
has minimum value 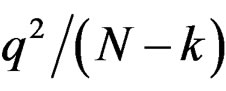 when
when  take the values in (18).
take the values in (18).
It follows that the upper bound of d is 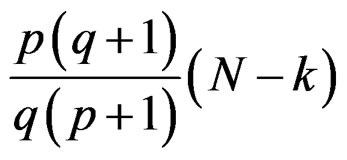
as desired. The theorem is proved.
Proof of Theorem 3 Since  and
and 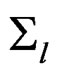 denote the mean vector and covariance matrix of
denote the mean vector and covariance matrix of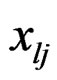 , we let
, we let 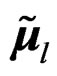 and
and 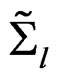 denote the mean vector and covariance matrix of the affine-transformed responses
denote the mean vector and covariance matrix of the affine-transformed responses 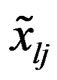 given by (16). Then we have
given by (16). Then we have 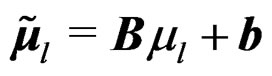 and
and 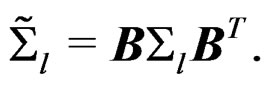 It follows that
It follows that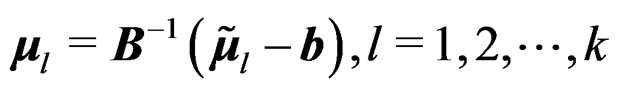 . As we defined the long mean vector
. As we defined the long mean vector 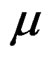 and the big covariance matrix
and the big covariance matrix 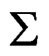 in Section 2, we define
in Section 2, we define  and
and 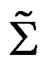 similarly. Then we have
similarly. Then we have 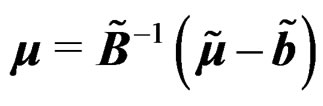 and
and 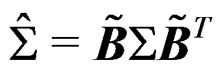 where
where  and
and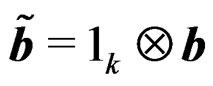 . It follows that the GLHT problem (3) can be equivalently expressed as
. It follows that the GLHT problem (3) can be equivalently expressed as
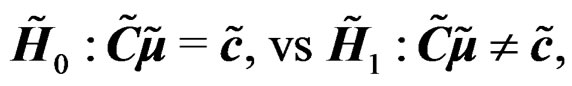
where 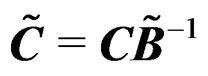 and
and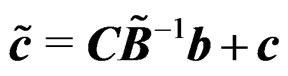 .
.
Since  and
and 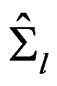 denote the unbiased estimators of
denote the unbiased estimators of 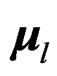 and
and  for the original responses
for the original responses , we define
, we define 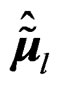 and
and 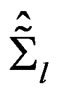 as the unbiased estimators of
as the unbiased estimators of  and
and  for the affine-transformed responses
for the affine-transformed responses 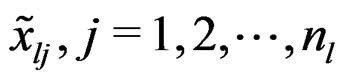 . Then by the affine-transformation (16), it is easy to see that
. Then by the affine-transformation (16), it is easy to see that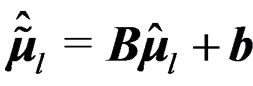 , and
, and 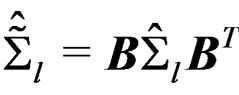 Therefore,
Therefore, 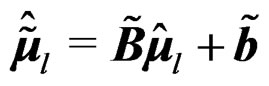 and
and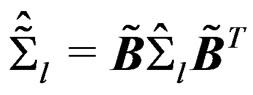 . Using the above, we have
. Using the above, we have 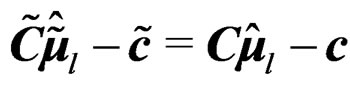 and
and . The affine-invariance of T follows immediately.
. The affine-invariance of T follows immediately.
To show that 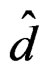 is affine-invariant, by (13), it is sufficient to show that
is affine-invariant, by (13), it is sufficient to show that 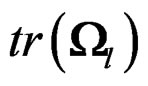 and
and 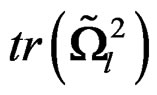 are affine-invariant. Let
are affine-invariant. Let 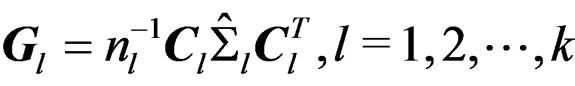 and
and . Then we have
. Then we have 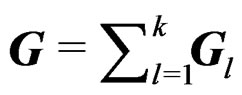 and
and 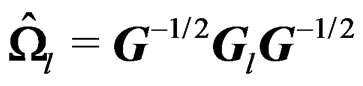 . It follows that
. It follows that 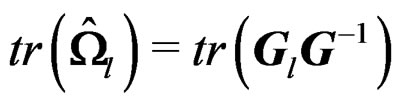 and
and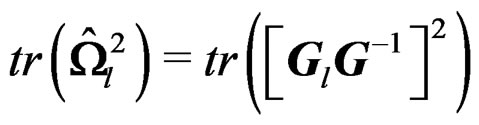 . Since G is affine-invariant, we only need to show that
. Since G is affine-invariant, we only need to show that 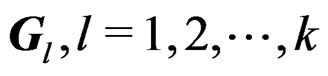 are affine-invariant. Since
are affine-invariant. Since 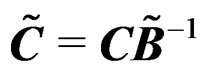 implies
implies 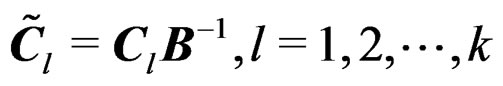 and
and 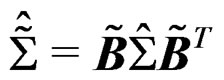 implies
implies  , the affine-invariance of
, the affine-invariance of 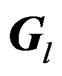 follows immediately. The theorem is then proved.
follows immediately. The theorem is then proved.
Proof of Theorem 4 First of all, under the transformation (17), we have 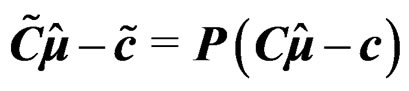 and
and 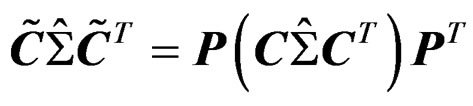 . The invariance of T under (17) follows immediately.
. The invariance of T under (17) follows immediately.
To show that 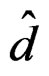 is invariant under the transformation (17), by (13), it is sufficient to show that
is invariant under the transformation (17), by (13), it is sufficient to show that 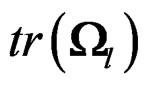 and
and 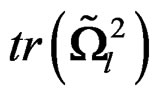 are invariant under (17). The transformation (17) implies that
are invariant under (17). The transformation (17) implies that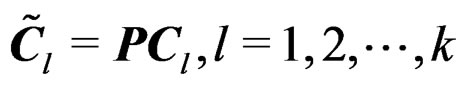 . Then we have
. Then we have 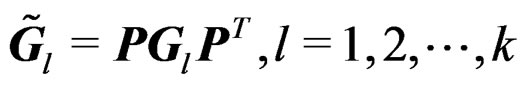 and
and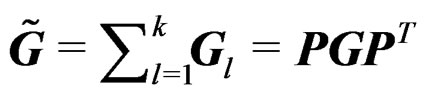 . It follows that
. It follows that 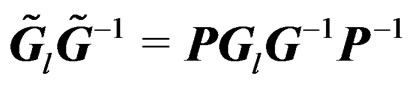 so that
so that
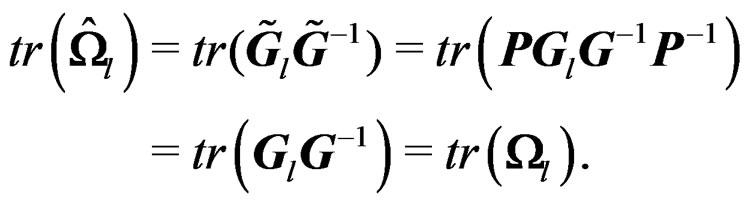
Similarly, we can show that . This proves that
. This proves that 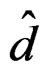 is invariant under the transformation (17). The theorem is then proved.
is invariant under the transformation (17). The theorem is then proved.
Proof of Theorem 5 Let 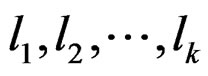 be any permutation of
be any permutation of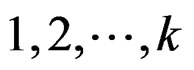 . Then it is easy to see that
. Then it is easy to see that

showing that ,
, 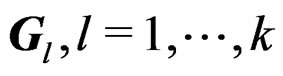 , and
, and 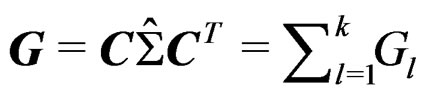 are invariant under different labeling schemes of the mean vectors and so is the Wald-type test statistic T.
are invariant under different labeling schemes of the mean vectors and so is the Wald-type test statistic T.
To show that  is invariant under different labeling schemes of the group mean vectors, by (13), it is sufficient to show that the denominator of
is invariant under different labeling schemes of the group mean vectors, by (13), it is sufficient to show that the denominator of 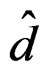 has such a property. This is actually the case by noticing that the denominator of
has such a property. This is actually the case by noticing that the denominator of 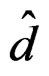
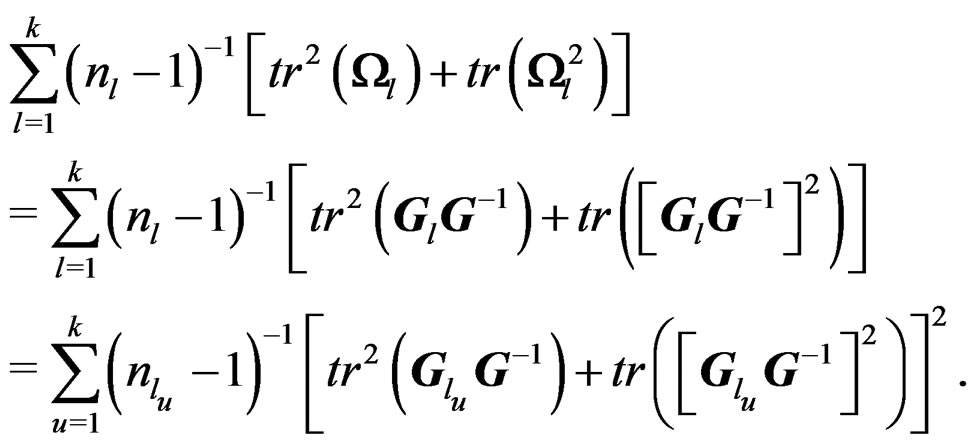
This completes the proof of the theorem.
6. Acknowledgements
The work was supported by the National University of Singapore Academic Research Grant R-155-000-108-112. The author thanks the Editor for helpful comments and suggestions that help improve the presentation of the paper.
REFERENCES
- S. Johansen, “The Welch-James Approximation to the Distribution of the Residual Sum of Squares in a Weighted linear Regression,” Biometrika, Vol. 67, No. 1, 1980, pp. 85-95. doi:10.1093/biomet/67.1.85
- K. Krishnamoorthy and F. Lu, “A Parametric Bootstrap Solution to the MANOVA under Heteroscedasticity,” Journal of Statistical Computation and Simulation, Vol. 80, No. 8, 2010, pp. 873-887. doi:10.1080/00949650902822564
- T. W. Anderson, “An Introduction to Multivariate Statistical Analysis,” Wiley, New York, 2003.
- K. Krishnamoorthy and Y. Xia, “On Selecting Tests for Equality of Two Normal Mean Vectors,” Multivariate Behavioral Research, Vol. 41, No. 4, 2006, pp. 533-548. doi:10.1207/s15327906mbr4104_5
- K. Krishnamoorthy and J. Yu, “Modified Nel and van der Merwe Test for the Multivariate Behrens-Fisher Problem,” Statistics and Probability Letters, Vol. 66, No. 2, 2004, pp. 161-169. doi:10.1016/j.spl.2003.10.012
- G. S. James, “Tests of Linear Hypotheses in Univariate and Multivariate Analysis When the Ratios of the Population Variances Are Unknown,” Biometrika, Vol. 41, No. 1-2, 1954, pp. 19-43.
- Y. Yao, “An Approximate Degrees of Freedom Solution to the Multivariate Behrens-Fisher Problem,” Biometrika, Vol. 52, 1965, pp. 139-147.
- D. G. Nel and C. A. van der Merwe, “A Solution to the Multivariate Behrens-Fisher Problem,” Communication Statistics: Theory and Methods, Vol. 15, No. 12, 1986, pp. 3719-3735. doi:10.1080/03610928608829342
- S. Kim, “A Practical Solution to the Multivariate BehrensFisher Problem,” Biometrika, Vol. 79, No. 1, 1992, pp. 171-176. doi:10.1093/biomet/79.1.171
- H. Yanagihara and K. H. Yuan, “Three Approximate Solutions to the Multivariate Behrens-Fisher Problem,” Communication Statistics: Simulation and Computation, Vol. 34, No. 4, 2005, pp. 975-988. doi:10.1080/03610910500308396
- A. Belloni and G. Didier, “On the Behrens-Fisher Problem: A Globally Convergent Algorithm and a FiniteSample Study of the Wald, LR and LM Tests,” Annals of Statistics, Vol. 36, No. 5, 2008, pp. 2377-2408. doi:10.1214/07-AOS528
- W. F. Christensen and A. C. Rencher, “A Comparison of Type I Error Rates and Power Levels for Seven Solutions to the Multivariate Behrens-Fisher Problem,” Communication Statistics: Theory and Methods, Vol. 26, 1997, pp. 1251-1273.
- B. L. Welch, “On the Comparison of Several Mean Values: An Alternative Approach,” Biometrika, Vol. 38, 1951, pp. 330-336.
- J. Gamage, T. Mathew and S. Weerahandi, “Generalized p-Values and Generalized Confidence Regions for the Multivariate Behrens-Fisher Problem and MANOVA,” Journal of Multivariate Analysis, Vol. 88, No. 1, 2004, pp. 177-189. doi:10.1016/S0047-259X(03)00065-4
- K. L. Tang and J. Algina, “Performing of Four Multivariate Tests under Variance-Covariance Heteroscedasticity,” Multivariate Behavioral Research, Vol. 28, No. 4, 1993, pp. 391-405. doi:10.1207/s15327906mbr2804_1
- K. Krishnamoorthy, F. Lu and T. Mathew, “A Parametric Bootstrap Approach for ANOVA with Unequal Variances: Fixed and Random Models,” Computational Statistics and Data Analysis, Vol. 51, No. 12, 2007, pp. 5731-5742. doi:10.1016/j.csda.2006.09.039
- J. T. Zhang, “Tests of Linear Hypotheses in the ANOVA under Heteroscedasticity,” Manuscript, 2012.
- J. T. Zhang, “An Approximate Degrees of Freedom Test for Heteroscedastic Two-Way ANOVA,” Journal of Statistical Planning and Inference, Vol. 142, 2012, pp. 336-346.
- F. E. Satterthwaite, “An Approximate Distribution of Estimate of Variance Components,” Biometrics Bulletin, Vol. 2, No. 6, 1946, pp. 110-114. doi:10.2307/3002019
- J. T. Zhang, “Approximate and Asymptotic Distribution of χ2-Type Mixtures with Application,” Journal of American Statistical Association, Vol. 100, No. 469, 2005, pp. 273-285. doi:10.1198/016214504000000575
- A. M. Kshirsagar, “Multivariate Analysis,” Marcel Decker, New York, 1972.

