Open Journal of Statistics
Vol.1 No.3(2011), Article ID:8065,6 pages DOI:10.4236/ojs.2011.13016
Asymptotic Analysis for U-Statistics and Its Application to Von Mises Statistics
Faculty of Computational Mathematics and Cybernetics, Moscow State University, Moscow, Russia
E-mail: tzubayraev@gmail.com
Received July 30, 2011; revised August 31, 2011; accepted September 14, 2011
Keywords: U-Statistics, Von Mises Statistics, Symmetric Statistics
Abstract
Let 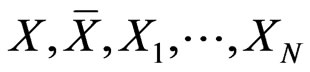 be i.i.d. random variables taking values in a measurable space (
be i.i.d. random variables taking values in a measurable space (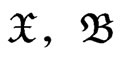 ). Let
). Let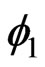 :
: 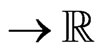
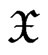 and
and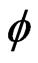 :
: 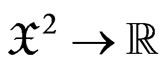 be measurable functions. Assume that
be measurable functions. Assume that 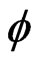 is symmetric, i.e.
is symmetric, i.e.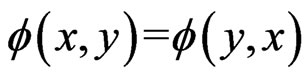 , for any
, for any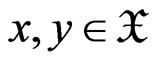 . Consider U-statistic
. Consider U-statistic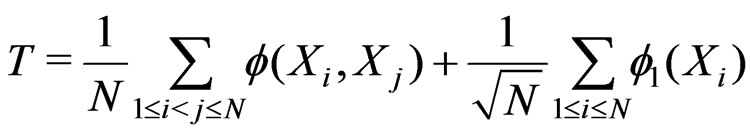 , assuming that
, assuming that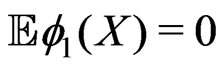 ,
, 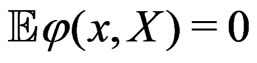 for all
for all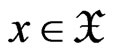 ,
, 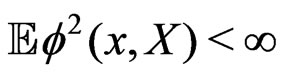 ,
,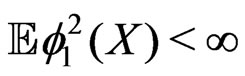 . We will provide bounds for
. We will provide bounds for 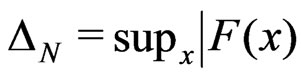
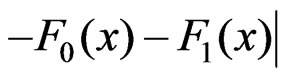 , where
, where 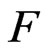 is a distribution function of
is a distribution function of 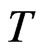 and
and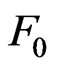 ,
, 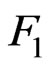 are its limiting distribution function and Edgeworth correction respectively. Applications of these results are also provided for von Mises statistics case.
are its limiting distribution function and Edgeworth correction respectively. Applications of these results are also provided for von Mises statistics case.
1. Introduction
Consider the measurable space (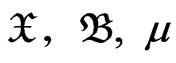 ), with measure
), with measure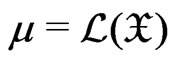 . Let
. Let 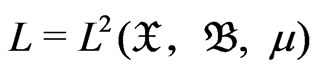 denote the real Hilbert space of square integrable real functions. Let
denote the real Hilbert space of square integrable real functions. Let 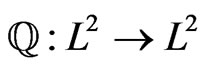 denote the Hilbert-Schmidt operator associated with the kernel
denote the Hilbert-Schmidt operator associated with the kernel 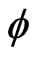 and defined via
and defined via
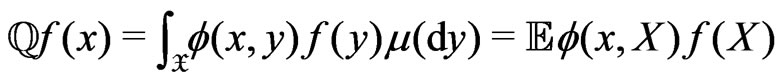
Let 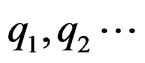 be its eigenvalues. Without loss of generality we shall assume that
be its eigenvalues. Without loss of generality we shall assume that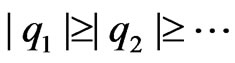 .
.
Let 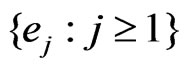 denote an orthonormal complete system of eigenfunctions of
denote an orthonormal complete system of eigenfunctions of  of the corresponding eigenvalues
of the corresponding eigenvalues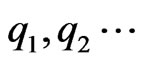 . Then
. Then
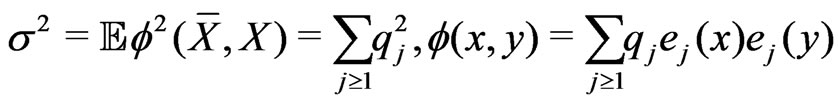 (1.1)
(1.1)
since  is a Hilbert-Schmidt operator and the kernel
is a Hilbert-Schmidt operator and the kernel  is degenerate. The series in (1.1) converges in
is degenerate. The series in (1.1) converges in 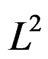
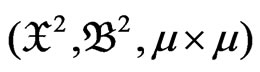 . Consider the subspace
. Consider the subspace 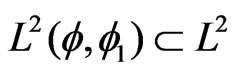
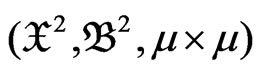 generated by
generated by 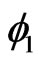 and eigenfunctions
and eigenfunctions 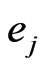 corresponding to nonzero eigenvalues
corresponding to nonzero eigenvalues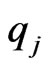 . Introducing, if necessary, an eigenvalues
. Introducing, if necessary, an eigenvalues 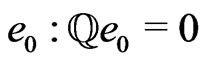 ,we can assume that
,we can assume that 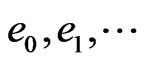 is an orthonormal basis in
is an orthonormal basis in 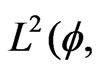
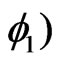 . Thus, we have
. Thus, we have
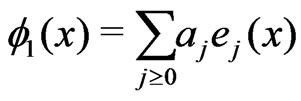 in
in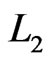 ,
, 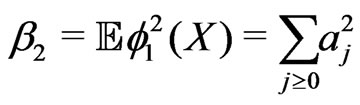 ,(1.2)
,(1.2)
with 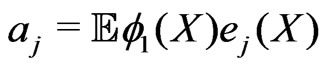 and
and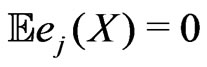 , for all j. Therefore
, for all j. Therefore 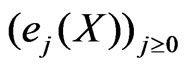 is an orthonormal system of random variables with zero means.
is an orthonormal system of random variables with zero means.
Hilbert space 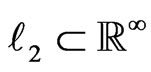 consists of
consists of 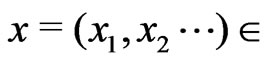
 , such that
, such that
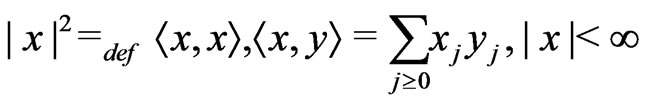 .
.
Consider the random vector
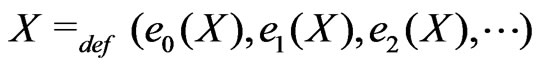 ,(1.3)
,(1.3)
which takes values in . Since
. Since 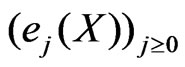 is a system of mean zero uncorrelated random variables with variances 1, the random vector
is a system of mean zero uncorrelated random variables with variances 1, the random vector 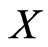 has mean zero and
has mean zero and 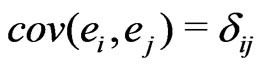 and
and 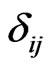 is Kronecker’s symbol. Using (1.1) and (1.2), we can write
is Kronecker’s symbol. Using (1.1) and (1.2), we can write
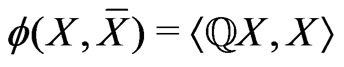 ,
, 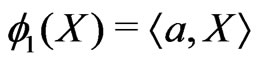 , (1.4)
, (1.4)
where we define 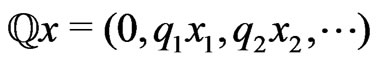 for
for 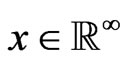 and
and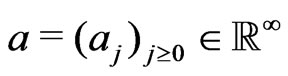 . The equalities (1.4) allow us to assume that the measurable space
. The equalities (1.4) allow us to assume that the measurable space 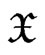 is
is . Let
. Let 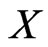 be a random vector taking values in
be a random vector taking values in  with mean zero and covariance
with mean zero and covariance 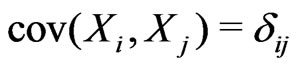 and that
and that
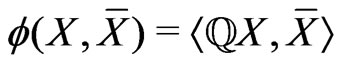 ,
,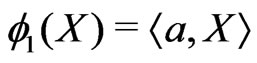 . (1.5)
. (1.5)
Without loss of generality we shall assume that the kernels 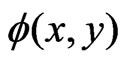 and
and 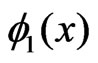 are linear functions in each of their arguments ([2]).
are linear functions in each of their arguments ([2]).
Introduce the definitions:
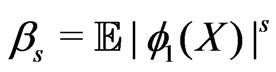 ,
, 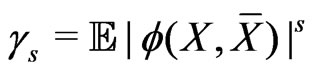 ,
, 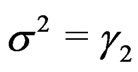 ,
, 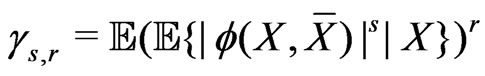 and assume that
and assume that
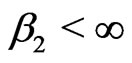 ,
,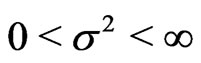 .
.
for the statistic  we can write
we can write
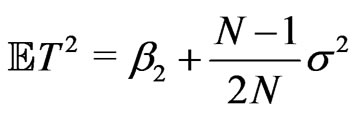 .
.
The statistic  is called degenerate since
is called degenerate since  ensures that the quadratic part of the statistic is not asymptotically negligible and therefore statistic
ensures that the quadratic part of the statistic is not asymptotically negligible and therefore statistic  is not asymptotically normal. More precisely, the asymptotic distribution of
is not asymptotically normal. More precisely, the asymptotic distribution of 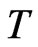 is non-Gaussian and is given by the distribution of the random variable
is non-Gaussian and is given by the distribution of the random variable
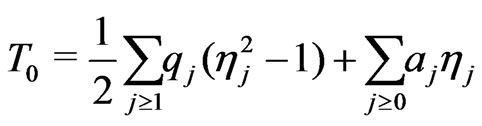 ,(1.6)
,(1.6)
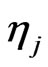 is a sequence of i.i.d. standard normal variables,
is a sequence of i.i.d. standard normal variables, 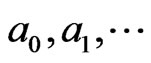 denotes a sequence of square summable weights and
denotes a sequence of square summable weights and 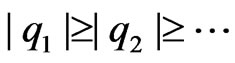 denote eigenvalues of the Hilbert-Schmidt operator, say
denote eigenvalues of the Hilbert-Schmidt operator, say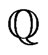 , associated with the kernel
, associated with the kernel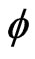 .
.
Consider the concentration functions of statistic 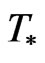
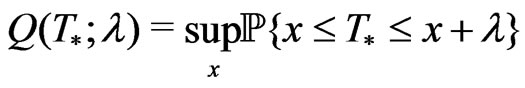 ,
, 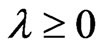 ,(1.7)
,(1.7)
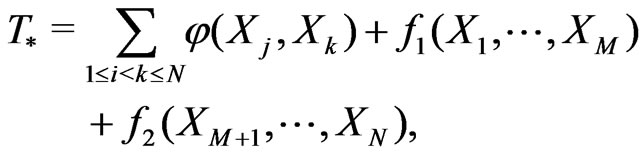
where 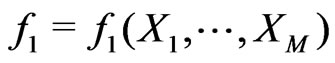 is an arbitrary statistic depending only on
is an arbitrary statistic depending only on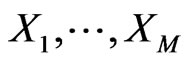 ,
, 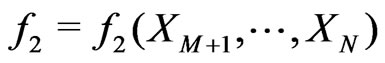 is as well arbitrary but independent of
is as well arbitrary but independent of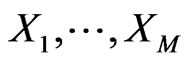 . Note that the class of statistics
. Note that the class of statistics 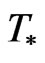 is slightly more general than the class of statistics T. We shall denote
is slightly more general than the class of statistics T. We shall denote 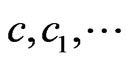 constants. If a constant depends on, say s, we shall write
constants. If a constant depends on, say s, we shall write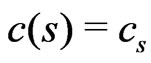 .
.
Consider the distibution functions
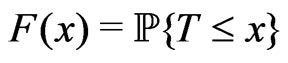 ,
, 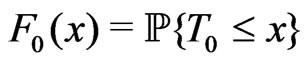 ,
, 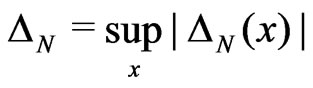 ,
, 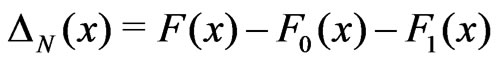 ,
,
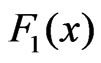 denotes an Edgeworth correction.The Edgeworth correction
denotes an Edgeworth correction.The Edgeworth correction 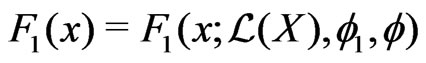 is defined as a function of bounded variation satisfying
is defined as a function of bounded variation satisfying 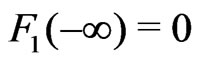 and with the Fourier-Stieltjes transform given by
and with the Fourier-Stieltjes transform given by
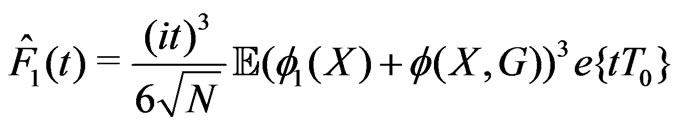 .
.
Let us notice that 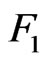 vanishes if
vanishes if 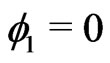 or if
or if
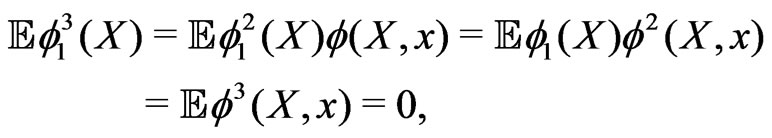 (1.8)
(1.8)
holds for all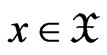 . Using the technique presented in this work we may obtain the result for approximation bound of order
. Using the technique presented in this work we may obtain the result for approximation bound of order 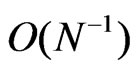 for U-statistic distribution function which has an order
for U-statistic distribution function which has an order 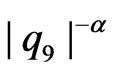 (see Theorem 3, 2) below) or
(see Theorem 3, 2) below) or 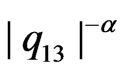 (see Theorem 3, 1) below) with respect to dependence on first nine or thirteen eigenvalues of operator
(see Theorem 3, 1) below) with respect to dependence on first nine or thirteen eigenvalues of operator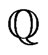 , respectively.
, respectively.
2. Auxiliary Results
Consider the vector 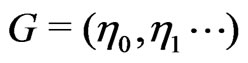 with values in
with values in , where
, where 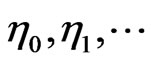 standard normal variables. Let us formulate lemma in which equalities for the moments of determinants of random matrices consisting of the scalar products such as
standard normal variables. Let us formulate lemma in which equalities for the moments of determinants of random matrices consisting of the scalar products such as 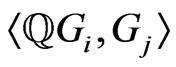 are obtained. Analogue of this lemma is proved in [1] for matrices consisting of the scalar products such as
are obtained. Analogue of this lemma is proved in [1] for matrices consisting of the scalar products such as 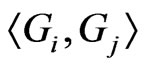 where G-Gaussian
where G-Gaussian 
 vector.
vector.
Lemma 1. Let 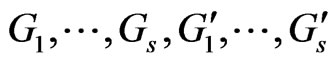 be random elements in a Hilbert space
be random elements in a Hilbert space 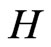 such that
such that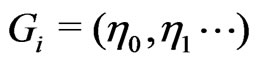 , where
, where 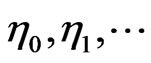 standard normal variables. Let
standard normal variables. Let 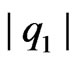
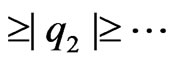 be the eigenvalues of Hilbert-Schmidt operator
be the eigenvalues of Hilbert-Schmidt operator .
.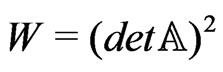 , where
, where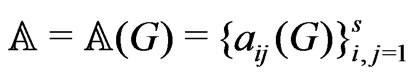 ,
,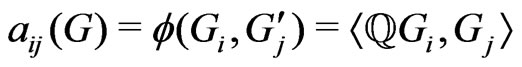 .
.
Then
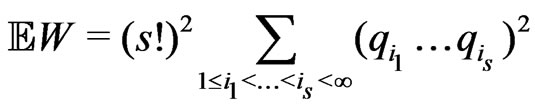 ,
,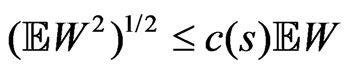 .
.
Nondegeneracy condition
We shall assume that random vector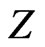 , a kernel
, a kernel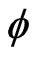 , parameters
, parameters 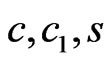 and
and 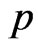 satisfy the nondegeneracy condition if
satisfy the nondegeneracy condition if
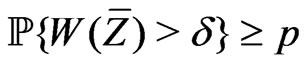 ,
,  ,
,
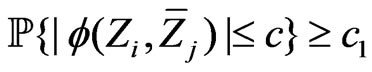 ,
,  ,
,  ,(2.1)
,(2.1)
where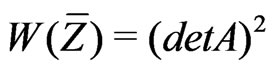 ,
, 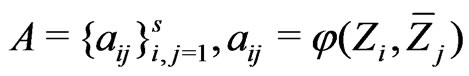 ,
, 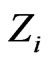 ,
, 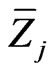 are independent copies of
are independent copies of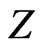 .
.
Here parameter 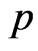 is small and parameter
is small and parameter 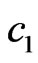 is close to 1. Let
is close to 1. Let 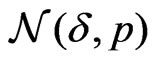 denote the set of all vectors
denote the set of all vectors 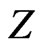 satisfying the nondegeneracy condition.
satisfying the nondegeneracy condition.
Notice that 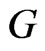 satisfies the nondegeneracy condition. Let vectors
satisfies the nondegeneracy condition. Let vectors 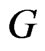 and
and 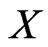 have equal means and covariances, then
have equal means and covariances, then
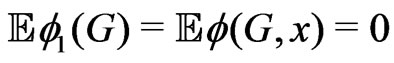 ,
, 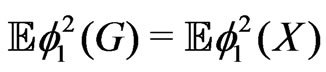 ,
,
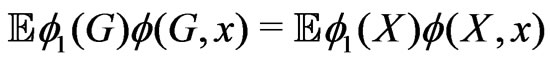 ,
,
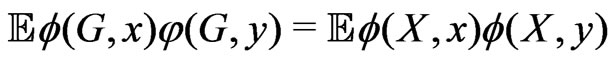 .
.
The following Lemma 2 means that increase of 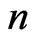 yields equivalence of nondegeneracy conditions fulfillments for sum and Gaussian vector.
yields equivalence of nondegeneracy conditions fulfillments for sum and Gaussian vector.
Lemma 2. Let 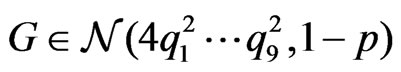 be a Gaussian random vector and
be a Gaussian random vector and
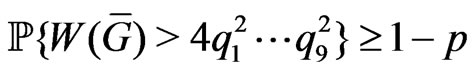 . Then for
. Then for 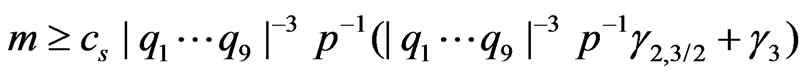 we have
we have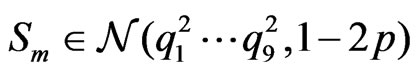 , where
, where 
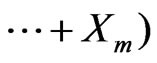 is random sum.
is random sum.
Further, it is necessary to bound the characteristic function of the statistic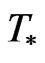 . That will be done in Lemmas 3, 4 and Theorem 1.
. That will be done in Lemmas 3, 4 and Theorem 1.
The following Lemma 3 has a similar proof to Lemma 6.5 from [2].
By 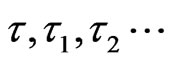 we shall denote independent copies of a symmetric random variable
we shall denote independent copies of a symmetric random variable 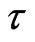 with nonnegative characteristic function and such that
with nonnegative characteristic function and such that
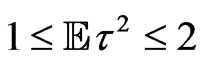 ,
,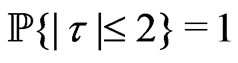 .(2.2)
.(2.2)
Lemma 3. Let 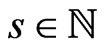 and
and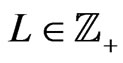 . Assume that vector
. Assume that vector 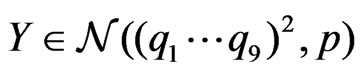 takes values in
takes values in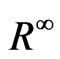 . Write
. Write
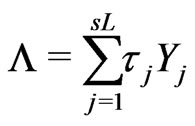 ,
, 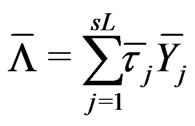 ,
, 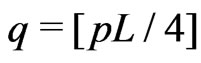 where
where 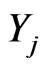 and
and 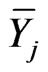 are independent copies of Y. Then
are independent copies of Y. Then
 ,
, 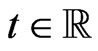 ,
, 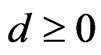 where
where 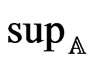 denotes the supremum over all
denotes the supremum over all 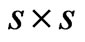 nonrandom matrices
nonrandom matrices  such that
such that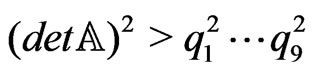 .
.
U and V denote independent vectors in 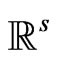 which are sums of n independent copies of
which are sums of n independent copies of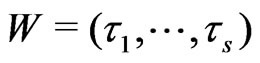 .
.
In the following lemma the bound from above for the characteristic function 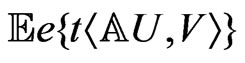 is received. This results was proved in [1]. The received estimation contains the determinant of matrix in right-hand side of inequality. This fact allows to use eigenvalues of operator
is received. This results was proved in [1]. The received estimation contains the determinant of matrix in right-hand side of inequality. This fact allows to use eigenvalues of operator 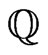 for the estimation of characteristic function.
for the estimation of characteristic function.
Lemma 4. Let A be a nondegenerate 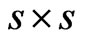 matrix. Let
matrix. Let 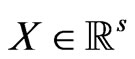 denote a random vector with covariance
denote a random vector with covariance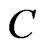 . Assume that there exists a constant
. Assume that there exists a constant 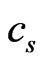 such that
such that
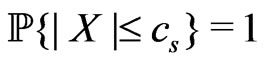 ,
, 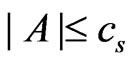 ,
,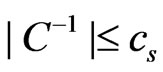 .(2.3)
.(2.3)
Let 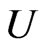 and
and 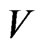 denote independent random vectors which are sums of n independent copies of
denote independent random vectors which are sums of n independent copies of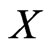 . Then
. Then
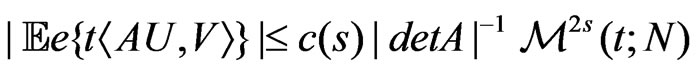 for
for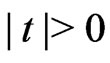 , where
, where 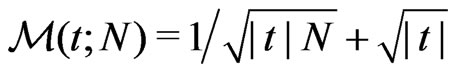 for
for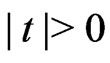 .
.
Using our Lemmas 3 and 4 we may obtain a bound for characteristic function for statistic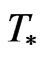 .
.
Theorem 1. Let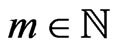 . Assume that the sum
. Assume that the sum 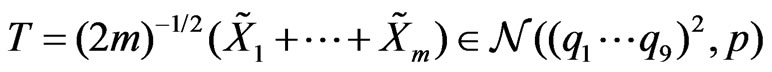 . Then, for any statistic
. Then, for any statistic 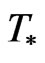 we have
we have
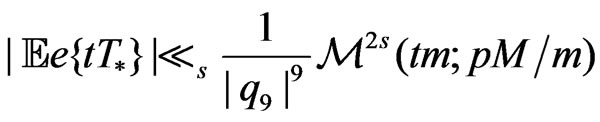 .
.
The proof of this theorem is similar to proof of Theorem 6.2 in [2].
Write :
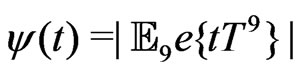 .(2.4)
.(2.4)
In following lemma a multiplicative inequality for characteristic function of 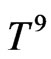 is given. This inequality yields the desired bound
is given. This inequality yields the desired bound 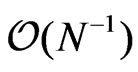 for an integral of the characteristic function of a U-statistic. Similar result was proved in Lemma 7.1 in [2]
for an integral of the characteristic function of a U-statistic. Similar result was proved in Lemma 7.1 in [2]
Lemma 5. Let 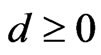 and
and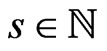 . Assume that
. Assume that 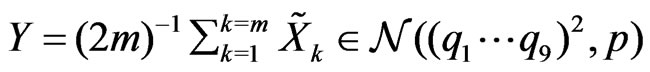 . Then there exist constants
. Then there exist constants 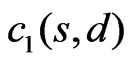 and
and 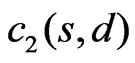 such that the event
such that the event
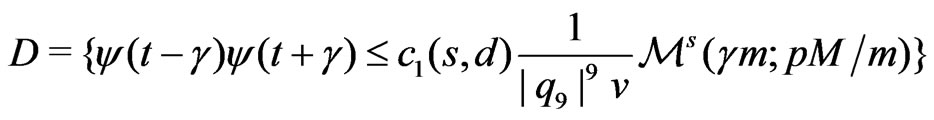 ,(2.5)
,(2.5)
satisfies
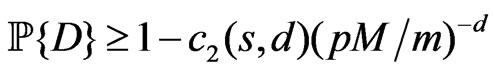 .(2.6)
.(2.6)
For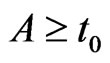 ,
, 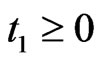 define the integrals
define the integrals
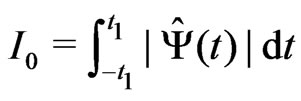 ,
,  where
where 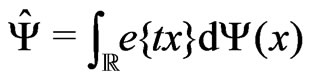 denotes the Fourier-Stieltjes transform of the distribution function
denotes the Fourier-Stieltjes transform of the distribution function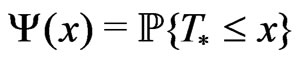 . The estimation for these integrals is received in following lemma, which has a proof similar to Lemma 3.3 in [2].
. The estimation for these integrals is received in following lemma, which has a proof similar to Lemma 3.3 in [2].
Lemma 6. Let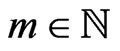 . Assume that the random vector
. Assume that the random vector
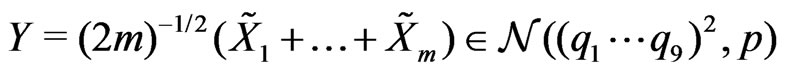 and
and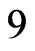
 . Let
. Let
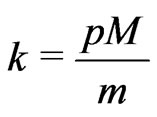 ,
, 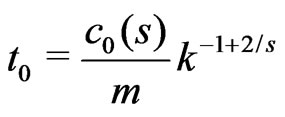 ,
, 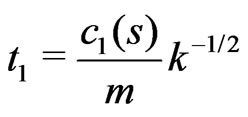 ,
, 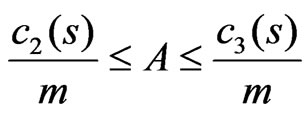 where
where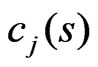 ,
, 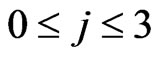 are some positive constants.
are some positive constants.
Then
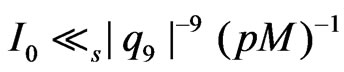 ,
,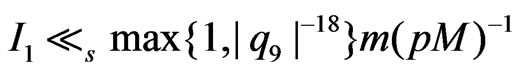 .(2.7)
.(2.7)
3. Approximation Accuracy Estimation
For 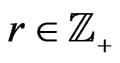 and functions
and functions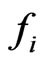 , introduce the statistic
, introduce the statistic
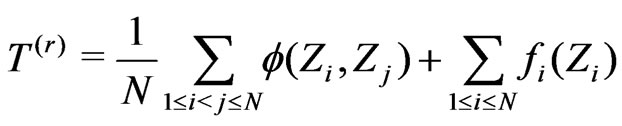 (3.1)
(3.1)
where
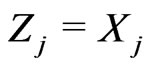 for
for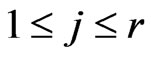 ,
, 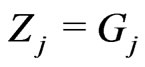 for
for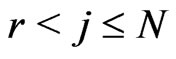 .
.
Write 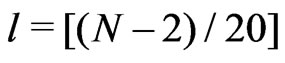 and put
and put
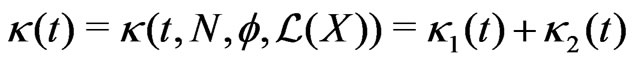 ,(3.2)
,(3.2)
where
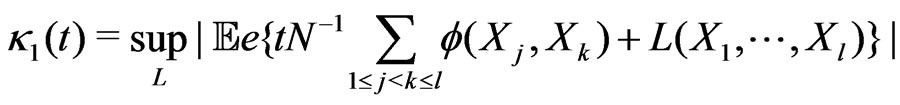 ,(3.3)
,(3.3)
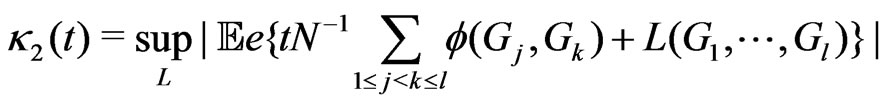 ,(3.4)
,(3.4)
where supremum is taken over all linear statistics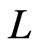 , that is, over all functions which can be represented as
, that is, over all functions which can be represented as 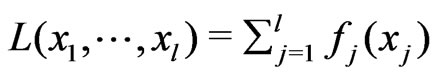 with some functions
with some functions 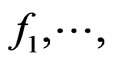
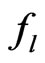 .
.
Consider the following Lemma 7, which has a similar proof as Lemma 4.2 in [2].
Lemma 7. Let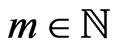 ,
, 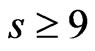 and
and 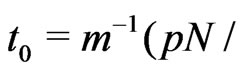
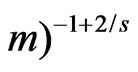 . Assume that the random vector
. Assume that the random vector 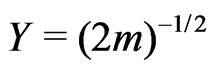
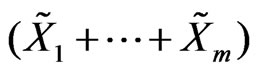 satisfies the nondegeneracy condition. Then, for
satisfies the nondegeneracy condition. Then, for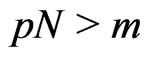 ,
, 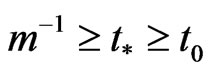 the distribution function
the distribution function 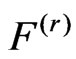 of
of 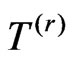 satisfies
satisfies
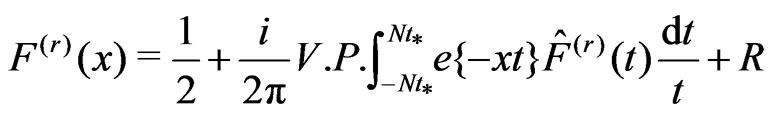 ,(3.5)
,(3.5)
where .
.
The Edgeworth correction 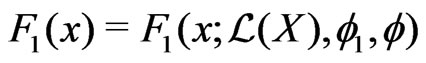 is defined as a function of bounded variation satisfying
is defined as a function of bounded variation satisfying 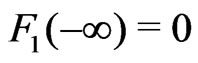 and with the Fourier-Stieltjes transform given by
and with the Fourier-Stieltjes transform given by
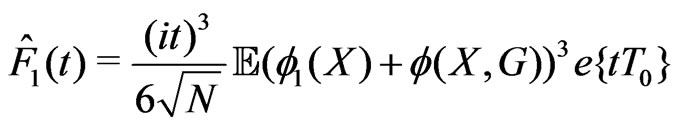 .(3.6)
.(3.6)
Lemma 8. Assume that the nondegeneracy condition is fulfilled.
1) Let 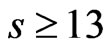 and
and 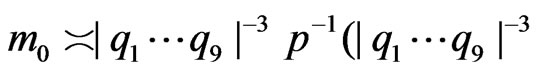
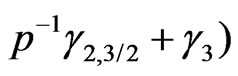 . Then
. Then
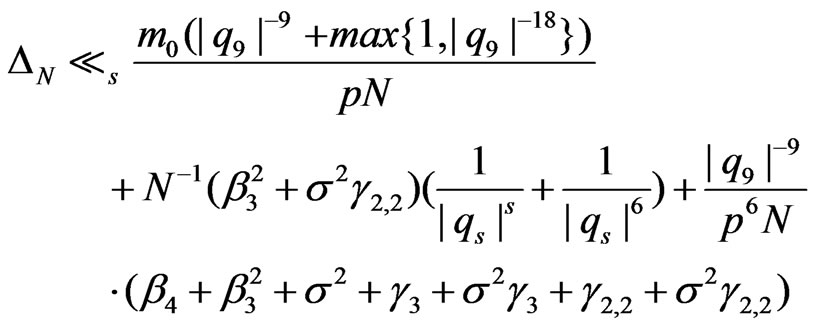 (3.7)
(3.7)
2) Assume that the condition (1.8) holds and that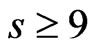 . Then
. Then
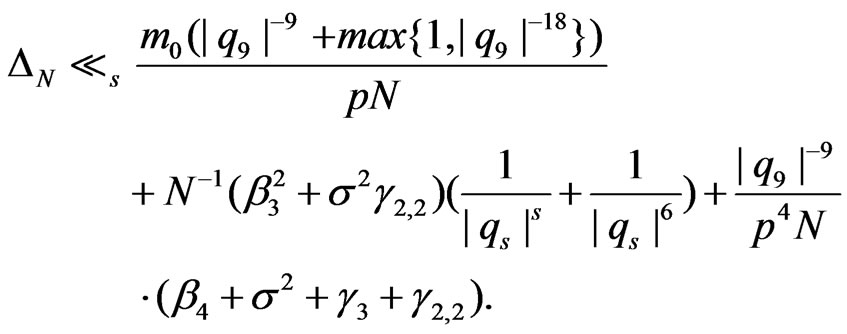 (3.8)
(3.8)
To prove this lemma we need to make the same steps as in Lemma 4.1 in [2] replacing Theorem 6.2 by Theorem 1.
Now we can formulate a following Theorem 2, where bounds for 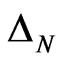 are obtained. This theorem were proved in [4]:
are obtained. This theorem were proved in [4]:
Theorem 2. 1) Let 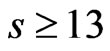
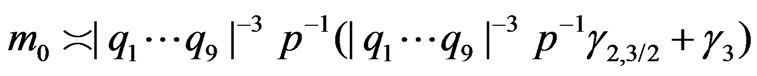 ,
,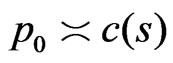 . Then
. Then
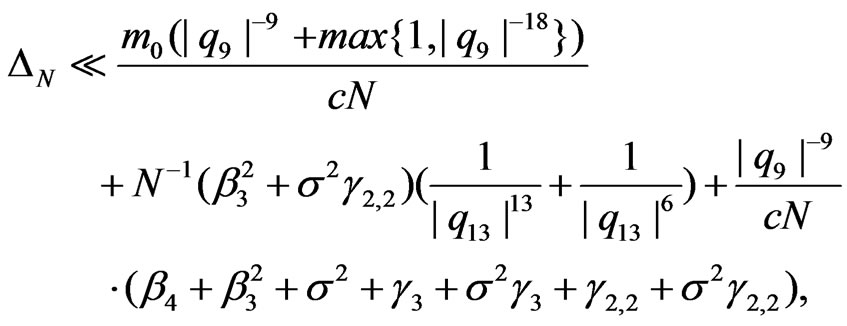 (3.9)
(3.9)
2) Assume that (1.8) holds and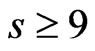 . Then
. Then
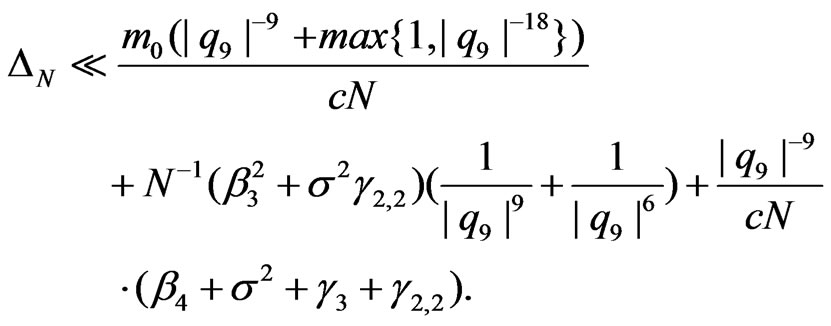 (3.10)
(3.10)
4. An Extension of Bounds to Von Mises Statistics. Applications
Assuming that the kernels 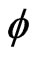 and
and 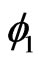 are degenerate, consider the von Mises statistic
are degenerate, consider the von Mises statistic
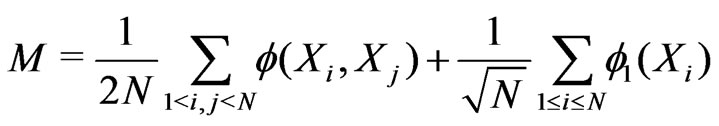 .(4.1)
.(4.1)
Introducing the function 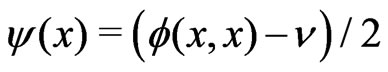 with
with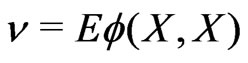 , we can rewrite (4.1) as
, we can rewrite (4.1) as
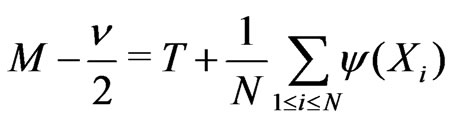 (4.2)
(4.2)
In this section we shall extend the bounds to statistics of type (4.2), assuming that 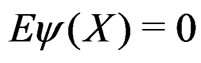 and
and 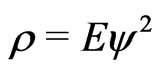
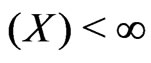 .
.
Similarly to the case of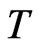 , we can represent the kernel
, we can represent the kernel 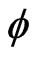 (respectively,
(respectively,  and
and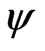 ) as a bilinear (respectively, linear) function, defined on
) as a bilinear (respectively, linear) function, defined on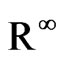 . However in this case we have to assume that
. However in this case we have to assume that 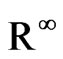 has an additional coordinate since
has an additional coordinate since 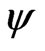 can be linearly independent of
can be linearly independent of 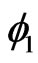 and of the eigenfunctions of
and of the eigenfunctions of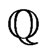 . To fix notation, we shall assume that
. To fix notation, we shall assume that 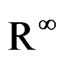 consists of vectors
consists of vectors 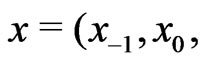
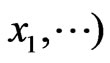 . Then all representations and results of Section 2 concerning
. Then all representations and results of Section 2 concerning 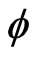 and
and 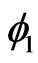 still hold, and for
still hold, and for 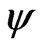 we have
we have 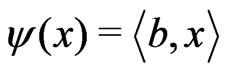 with some
with some 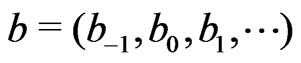 such that
such that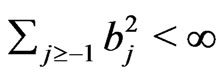 . Write
. Write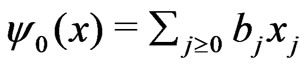 .
.
Introduce the function 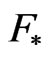 of bounded variation (provided that
of bounded variation (provided that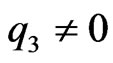 ) with the Fourier-Stieltjes transform
) with the Fourier-Stieltjes transform
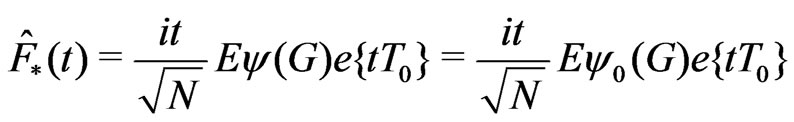
and such that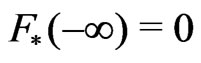 . Bellow we shall show that (see Lemma 9.3 [2])
. Bellow we shall show that (see Lemma 9.3 [2])
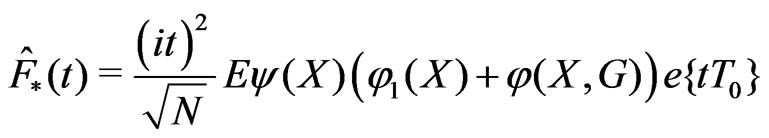 .(4.3)
.(4.3)
Notice that 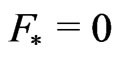 whenever
whenever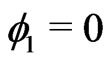 .
.
Write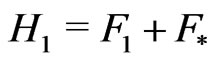 , and let
, and let 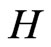 denote the distribution function of
denote the distribution function of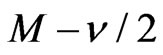 . Define
. Define
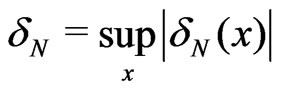 ,
,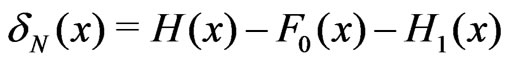 .
.
Theorem 3. 1) Assume that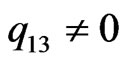 . Then we have
. Then we have
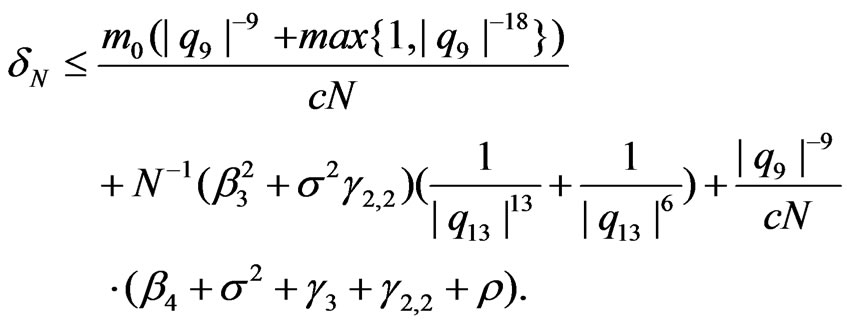 (4.4)
(4.4)
2) Assume that (1.8) is fulfilled and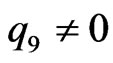 . Then we have
. Then we have
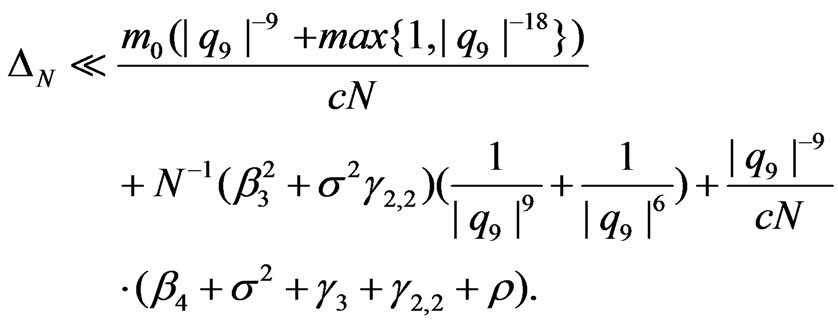
Proof. We shall use the following estimates. Write
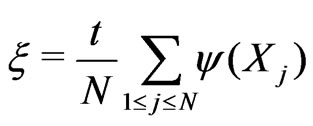 ,
,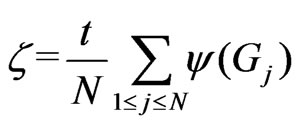 .(4.5)
.(4.5)
Expanding with remainder , splitting the sum
, splitting the sum  in parts and conditioning , we have
in parts and conditioning , we have
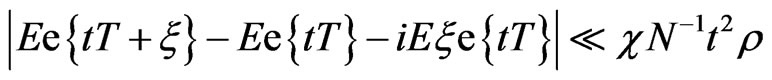 .(4.6)
.(4.6)
Proceeding similarly to the proof of Lemma 8.2 from [2], we obtain
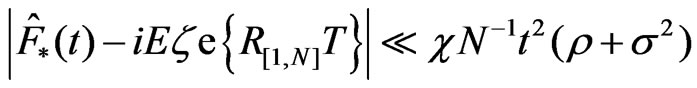 .(4.7)
.(4.7)
Applying the Bergstrom-type identity
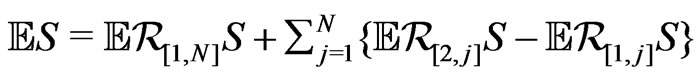 ,
,
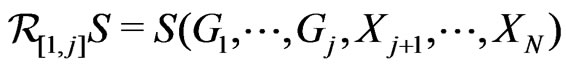
with 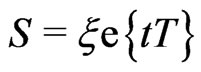 and proceeding similarly to the proof of Lemma 8.3 from [2], we get
and proceeding similarly to the proof of Lemma 8.3 from [2], we get
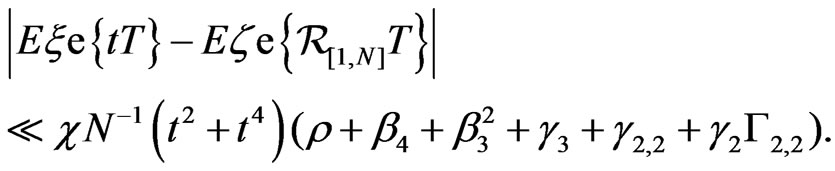 (4.8)
(4.8)
Arguments similar to the proof of Lemma 8.5 from [2] allow proving
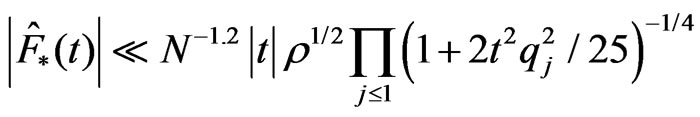 ,(4.9)
,(4.9)
and, for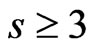 ,
,
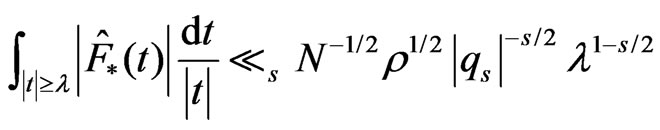 ,
,  (4.10)
(4.10)
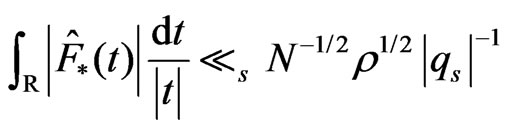 .(4.11)
.(4.11)
The estimates (4.6)-(4.11) allow proceeding similarly to the proof of Theorem 2, using a lemma similar to Lemma 8. Proving such a lemma, we have to apply Lemma 8 to the distribution function . This is possible since that statistic
. This is possible since that statistic 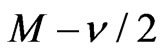 is a statistic of type (3.1). The estimates (4.10) and (4.11) allow application of the Fourier inversion to the function
is a statistic of type (3.1). The estimates (4.10) and (4.11) allow application of the Fourier inversion to the function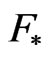 . As a result, we arrive at
. As a result, we arrive at
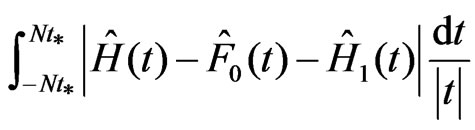 .
.
Here, however, we have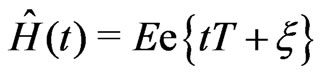 , and
, and
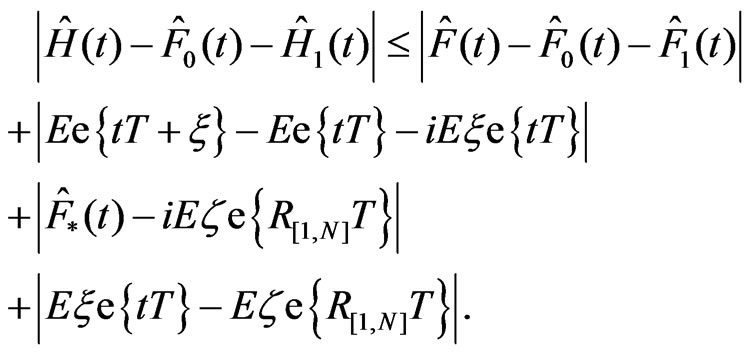 (4.12)
(4.12)
Therefore, using (4.6)-(4.8), we can proceed as in the proof of Lemma 11. As a final result we get bounds similar to those of Theorem 2, with the additional summand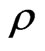 .
.
5. References
[1] V. Ulyanov and F. Götze, “Uniform Approximations in the CLT for Balls in Euclidian Spaces,” 00-034, SFB 343, University of Bielefeld, 2000, p. 26. http://www.math.uni-bielfeld.de/sfb343/preprints/pr00034.pdf.gz
[2] V. Bentkus and F. Götze, “Optimal Bounds in NonGaussian Limit Theorems for U-Statistics,” The Annals of Probability, Vol. 27, No.1, 1999, pp. 454-521. doi:10.1214/aop/1022677269
[3] S. A. Bogatyrev, F. Götze and V. V. Ulyanov, “NonUniform Bounds for Short Asymptotic Expansions in the CLT for Balls in a Hilbert Space,” Journal of Multivariate Analysis, Vol. 97, 2006, pp. 2041-2056.
[4] T. A. Zubayraev, “Asymptotic Analysis for U-Statistics: Approximation Accuracy Estimation,” Publications of Junior Scientists of Faculty of Computational Mathematics and Cybernetics, Moscow State University, Vol. 7, 2010, pp. 99-108. http://smu.cs.msu.su/conferences/sbornik7/smu-sbornik-7.pdf

