ABSTRACT

The paper introduces a theoretical model aimed to calculate the ionization energies of many electron atoms and their ions. The validity of the model, which implements the statistical formulation of the quantum uncertainty to infer a simple formula of ionization energy, has been already proven in a previous paper comparing systematically experimental and calculated values for elements with atomic numbers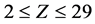, whose electron configurations include all ions with numbers 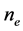of electrons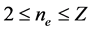. The present paper enhances and extends the results previously obtained; the approach is now generalized to include even the transition elements and in particular the lanthanides and actinides. The validity of the proposed model is proven examining all experimental data of ionization energies of these elements and their ions available in literature.

Keywords:

Quantum Chemistry, Energy Levels, Theoretical Model, Quantum Uncertainty, Relativity

1. Introduction

The calculation of the electron energy levels of atoms and ions is a challenging topic of quantum chemistry for its scientific [1] [2] and technological [3] importance. After the success of Bohr’s model, the next task was that of describing the many electron atoms. The first issue to be considered was then the mutual interaction between electrons. In the simplest case of He, for example, it is possible to calculate with classical methods the mutual repulsion energy between two electrons averaging the interaction between small elements of charge density of the first electron with that of the second electron in 1s orbitals [4] . Correcting the hydrogenlike binding energy of two electrons with this repulsive term, the ionization energy of one electron from the neutral atom was then 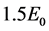with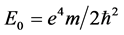. Yet this value, 20.42 eV, poorly agrees with the experimental value 24.58 eV. A full quantum mechanical approach appeared soon necessary, e.g. to take into account also the electron spins. To this purpose the orbitals of many-electron atoms are assumed similar to those of the hydrogenlike atom, so the quantum numbers are still suitable to describe the energy levels of the orbitals; however, whereas in H the electron energy depends essentially on n only, in a many-electron configuration the orbital energies depend in general on l and s, and m as well in the presence of an external field.

In general, the main problem of the theoretical approach to solve the wave equation of a cloud of electrons in the field of a nuclear charge is the electron correlation, due to the mutual interaction between electrons [5] . For example the Coulomb correlation concerns the spatial positions of electrons due to their repulsive interaction, whereas two electrons with parallel spins cannot be found at the same point in space according to the the so called Fermi correlation. Furthermore, a form of correlation is also related to the overall symmetry of the concerned quantum system. In principle the Schrödinger equation allows to take into account any effect possibly contributing to the electron energy level through an appropriate potential energy term, e.g. the mutual repulsion between electrons. However a simple analytical solution of the full Schrödinger equation does not exist because of the terms 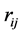expressing the mutual distances between the i-th and j-th electrons; approximation methods are necessary. As the chemical properties of atoms, and thus the pertinent group of the periodic table, are essentially controlled by the outer valence shells, a typical approximation is to replace the nuclear charge 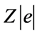with effective charge 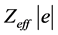accounting for the shielding effect of core electrons in the atom on the valence electrons.

The variety of effects involved to describe how the dynamics of one electron is perturbed by the interaction with the other ones requires in general a difficult mathematical formalism. Electron correlation is someway considered by the Hartree-Fock (HF) approximation via the exchange term of electrons with parallel spin, whose anti-symmetric wave function is approximated by a single Slater determinant. Exact wave functions, however, cannot generally be ex- pressed in this way. A single-determinant approximation does not take fully into account Coulomb correlation, so that the electron energy calculated via the non-relativistic Schrödinger equation is higher than its true value. Currently approximate methods of calculation of energy levels implement HF and post-HF computational models [6] , among which deserve to pay attention to the Con- figuration Interaction (CI) [7] and the Density Functional Theory (DFT) [8] [9] .

CI is a variational method to solve the non-relativistic Schrödinger equation of a multi-electron system, whose wave function is defined mathematically by a linear combination of Slater determinants. The interaction is introduced by mixing different electronic states, which specify the orbital occupation [10] . The CI calculations are suitable to describe small quantum systems because the method requires long calculation times.

Larger quantum systems are approachable via the density functional theory (DFT), which is used to describe the ground state of the electronic structure of many-body systems, consisting of single atoms or atoms in condensed phase. The properties of quantum systems are determined by functionals, i.e. functions of an appropriate function that typically represents the space distribution of electron density of an assigned electron configuration.

The calculation of the energy levels is particularly significant for the transition elements (TE) [11] , whose technological importance is acknowledged mostly in catalysis [12] and electronics [13] . From a quantum standpoint the “Aufbau” of quantum states leaves empty some orbitals, according to the idea that the ground state corresponds to the minimum configuration energy [14] .

In fact the “Aufbau” principle' is useful to account for the electronic structures of most atoms, yet it fails with some elements; the underlying theory is not generalizable “as such” to all elements of the periodic table [15] . The TE are characterized by the nd electron shell partially filled; this determines their positions in the periodic table. From a chemical point of view is interesting their chance of forming coordination compounds if a donor atom provides an electron that occupies an empty level; they act as Lewis acids to form complexes with a variety of Lewis bases. A coordination compound consists thus of one or more metal complexes, with a central metal atom/ion bonded to ions/molecules that contain one or more pairs of electrons shareable with the metal (ligands).

Are identifiable four d block elements that involve the 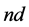and 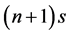levels. Owing to the energy of the level 4s lower than 3d, the electron configurations of elements with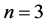, the first block includes elements from Sc to Ni, whereas Cu has the “regular” 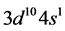ground level configuration. Analogous considerations hold for the second d block series involving the levels 4d and 5s of elements from Y to Ag.

At higher Z, are acknowledged in the periodic table two more series, the so called 5d and 6d block series, known as lanthanides and actinides.The former includes elements from La to Hf through Au, the latter from Ac to Lr.

The Lanthanides have a similar outer shell electron configuration and thus physical similarities. The peculiarity of these TE is that they have electrons in the f orbital. After La the energy of the 4f sub-shell is slightly lower than that of the 5d sub-shell; so the electrons fill the former sub-shell before the latter. This causes the so called lanthanide contraction, where the 5s and 5p orbitals penetrate the 4f sub-shell; so the 4f orbital is not shielded from the increasing nuclear change, i.e. the atomic radius of the atom decreases throughout the series. This fact affects the ease at which lanthanides lose electrons, i.e. their basicity and thus their reactivity with other elements. The basicity decreases at increasing atomic numbers, which explains the different solubility of their salts and the formation of the complex species and their magnetic properties depending on whether the electrons are paired or unpaired.

In the actinide series the energy in the 6d orbitals is lower in energy than in the 5f orbitals. Despite the energy gap between the 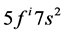and 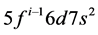configurations is small, the electrons fill preferentially 5f orbital, 6d orbital and then 7s orbital.

The 5f orbitals are not shielded by the filled 6s and 6p sub shells and do not shield effectively each other from the nucleus; their energies decrease rapidly at increasing atomic numbers.

It is clear that the ground energy levels of these TE and their ions are the key to explain the configuration sequences at increasing Z and thus their chemical and physical properties. On the one hand, investigating the electron structure of TE is challenging from a theoretical point of view. While the general idea is clear, i.e. the stable state corresponds to that of minimum energy, the calculation of the energy levels is very complex mostly because are involved several electrons; also, the schematic approximation of inner shell and outer shell, acceptable for example in the case of the alkali metals, is doubtful because the anomalous “Aufbau” involves inner d, f and s shells with several electrons. On the other hand, this topic has crucial technological implications: the diamagnetic or paramagnetic properties of the various elements depend on their electron configurations, as well as the catalytic properties and the ability to form coordination compounds and importance in electronics [16] . Is comprehensible thus the usefulness of investigating in particular the energy levels and ionization energies of TE, even at the scale of isolated ions/elements only, through a general and systematic calculation scheme.

It is worth quoting in this respect a possible theoretical approach alternative to CI and DFT based on the statistical formulation of the quantum space time uncertainty [17] , initially aimed to describe isolated atoms/ions and successively extended to the diatomic molecules [18] . The approach proposed here is an extension and enhancement of the previous model, purposely aimed to include the TE. Indeed the validity of the model was preliminarily tested up to an electron configuration of atoms and their ions up to 29 electrons. In the quoted paper the elements examined were characterized according to the standard “Aufbau” principle; remained instead untested and unanswered the problem of verifying whether or not the model could also describe the peculiar filling sequence of the electron levels in the TE.

Just this is the purpose of the present paper.

2. Physical Background

This section reminds shortly a few crucial points of [17] to better understand the model proposed in this paper and make the following exposition as self contained as possible.

It is possible to describe the properties of many electron atoms/ions implementing uniquely the statistical formulation of the space time uncertainty

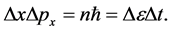(2.1)

The second equality follows from the former defining 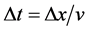and. Both equalities introduce uncertainty ranges of the respective dynamical variables, n is the number of allowed quantum states. All range sizes are by definition unknown and conceptually unknowable. For brevity this equation has been introduced as unique postulate of the model, despite it has been actually inferred as a corollary of an operative definition of space time [19] . The following remarks exemplify shortly on the one hand how to exploit the agnostic positions (2.1) replacing systematically the local dynamical variables with the respective uncertainty ranges, and on the other hand to show that the minimal information accessible in this way through Equation (2.1) only is in fact equivalent to that available through the usual operator formalism of wave mechanics.

The quantum angular momentum and energy of hydrogenlike atoms are concerned first.

The classical component of along an arbitrary direction defined by the unit vector w is, being the radial distance of any particle from the origin O of an arbitrary reference system R and its momentum. The positions and enable the number l of states to be calculated considering only the total ranges and of distances and momenta physically allowed to the particle, about which no hypothesis is necessary; instead the random local values and themselves have no physical interest. So, i.e. being; hence has itself a range of allowed values correspondingly to all local moduli of and. If and are orthogonal, then; else, rewriting as with, the component of along yields. Thus, according to Equation (2.1), , being l the usual notation for the integer quantum number of angular momentum. So is effectively a multi-valued function because of the uncertainties initially postulated for and. Moreover one component of only, e.g. along the z-axis, is knowable; repeating the same approach for the y and x components would trivially mean changing. Just this conclusion on the physical uniqueness of suggests that the average values, and should be equal; so the quantity of physical interest to describe the properties of quantum angular momentum is l, as a function of which is now inferred as well. The components averaged over the possible states summing from to, where L is an arbitrary maximum value of l, yield i.e.

Consider the quantum system formed by a particle in a central force field, e.g. an electron around a nuclear charge. Assuming the origin O of R on the nucleus, let be the classical electron energy, where m is the electron mass. As, putting again and, one finds. Two numbers of states, i.e. two quantum numbers, are expected because of the radial and angular uncertainties. In effect the eqs (2,1) and the quantum yield , which reads with and

. Minimize putting, which yields

(2.2)

and thus; so in order to get, i.e. a bound state. The reason of both ways to express will be explained in the section 6. Here are of interest the electron energy levels and rotational energy of the atom as a whole around O

(2.3)

It appears once more that neither the local coordinates nor the range sizes play any role in determining quantum angular momentum and energy levels. The physical meaning of is related to the early Bohr radius, i.e. is due to charges of opposite sign delocalized within a diametric distance apart.

Note that n and l are properties of the phase space, i.e. numbers of allowed quantum states; they describe the whole quantum system "nucleus + electron" rather than the nucleus and the electron separately, in agreement with the fact that nucleus and electron share a unique uncertainty radial range.

Consider now the identity. So it is consequently true that

(2.4)

where the last equation of the chain introduces the momentum p by dimensional reasons and reads

(2.5)

It shows the link between De Broglie momentum, Planck energy and condition, according which an integer number of steady electron wavelengths is defined along a circumference of radius along which the electron wave propagates at rate v. For such electron waves one finds

(2.6)

The first chain of equalities will be explained in the next section 6, in particular as concerns the evident link of and with. Note here that introducing to express the quantum energy levels implies defining the De Broglie momentum as a corollary: appears interesting that the energy levels of the system are linked to the kinetic energy of the electron moving along the circumference of radius via the coefficient. On the one hand, this result emphasizes the electromagnetic character of the interaction between electron and nucleus; comprehensibly is proportional to, as the coupling constant determines the force exerted in an interaction. On the other hand, it also appears that the key role of the quantum uncertainty in determining the allowed energy levels (2.6) also evidences the kind of interaction itself.

It has been shown in [17] that the approach based on the considerations of this section implies by consequence also the following expression of ionization energy

(2.7)

where is the current number of electrons in the atom/ion. Of course the present paper skips that trivially concerns the hydrogenlike ion. This equation has been calculated in the quoted paper taking a and b as universal constants

(2.8)

whereas one value of only was early taken as best fit constant for each electron configuration. The validity of the Equation (2.7) has been verified comparing calculated and experimental ionization energies for atomic numbers.

The previous model aimed essentially to show that the Equation (2.1) enable the ionization energies to be successfully calculated. This is understandable because in fact the Equations ((2.4) and (2.5)) show the chance of inferring in a natural way from the Equation (2.1) also the basic ideas of the quantum theory; moreover further fundamental concepts, e.g. the spin and the Pauli principle, can be deduced as corollaries, as it will be shown in the next section 6.

The enhanced model described in this paper aims to extend the range of atomic numbers and to overcome the best fit assumption about Q, whose physical meaning is introduced in a general way; the numerical value of Q is calculated in the conceptual frame of the model for all values of atomic numbers and electron configurations. So the input parameters of the model are the two constants (2.8) only.

In this paper the ionization energies are regarded with positive sign and expressed for simplicity of notation in units

(2.9)

All experimental data have been taken from [19] .

3. Outline of the Present Model

The Equation (2.7) admits two values of compatible with a given value of; calling and the solutions,

(3.1)

trivial manipulations of the Equation (2.7) yield

(3.2)

while also being

(3.3)

The reminder of this section aims to calculate and, thus removing the necessity of regarding them as mere numerical best fit parameters. Of course their values have variability ranges necessarily finite, see the next Equations ((3.8) and (3.9)), and should expectedly fulfill the reasonable boundary condition of minimum interaction energy between the electrons present in the shell. In other words, it is necessary not only to infer two equations to calculate them, but also to show how these equations are compliant with the given boundary condition. All this will highlight that the values of and have statistical meaning; they represent and summarize the link between and the average interaction energy. The calculations of these equations will be introduced in the next section 4.

Note now that

(3.4)

is calculable as a function of Z for a configuration of electrons and an appropriate quantum number n of the electron to be removed once knowing the constant a only. Hence

(3.5)

Since the energy of an electron hypothetically interacting with the nuclear charge only would be described by the mere hydrogenlike term, one infers that n governs not only but in principle also any form of interaction energy of the n_e-th electron with the other ones in the shell of residual electrons. Let be defined by

(3.6)

the fact of having extracted from the global energy (2.7) the amount of energy at the right hand side of the Equation (3.6), residual with respect to the binding hydrogenlike term and discrete itself according to n, implies that the quantization of the atom/ion requires the quantized correlation content involved by the Q terms. Just the result makes reasonable the Equation (3.6), as it introduces explicitly the distinctive property of the electron correlation: in principle, any calculation scheme that implements correlation terms taking arbitrary continuous energies seems “a priori” incompatible with the existence of discrete energy levels. Rather it appears conceptually sensible that the electron correlation resulting from all forms of interactions, whatever these latter might be, should be quantized itself. This consideration was in effect one of the starting points to formulate and propose the present model; it is anticipated here that just the quantities and include all necessary forms of correlation. Note that, strictly speaking, one could replace at the left hand side of the Equation (3.6) with the more accurate Dirac-like energy term; however the additional terms accounting for this correction can be included in an appropriate choice of or, as it will be shown below. These latter, indeed, are related to and directly calculable through. In this respect one equation has been already found, i.e. (3.4); a further equation is necessary.

To determine, proceed according to the basic ideas outlined in the previous section: nothing is known and knowable about local coordinates and mutual distances between the various electrons, whose positions change randomly, arbitrarily and unpredictably around the nucleus. Although the uncertainty prevents local information about their instantaneous repulsion energy, the previous considerations yield however the chance of defining the range allowed for the corresponding: it is reasonable to assume. The upper limit concerns the case where two electrons are so far apart each other that the ionization energy of one of them tends asymptotically to the hydrogenlike value, as anyway the i-th energy level cannot overcome that due to the mere binding effect of the nuclear charge. The lower limit concerns the case of two electrons approaching each other so closely that their mutual repulsion energy balances the binding energy, so that the ionization energy tends asymptotically to zero; this condition is necessary for the existence itself of the atom/ion. Expectedly, therefore, the true value of both and corresponding to the resulting ionization energy should fall within the respective intervals calculated replacing with and with 0 in the Equation (3.5). Hence for and one finds that turns respectively into

(3.7)

As this reasoning holds for both and, even and consist of two respective values. Figure 1 clarifies the dependence of upon in its allowed range of values and explains why is related to. Trivial manipulations with the help of the Equation (3.4) show that

(3.8)

(3.9)

both boundaries of the allowed ranges of and defined in this way are numerical limits calculable as a function of Z and and thus known.

Despite the total lack of information about position and momentum of the various electrons, it is possible to define the average ionization energy and calculate the average of the Equation (3.5) with respect to the possible values of

in an arbitrary range compatible with (3.8) and (3.9). By definition, one infers in general from the Equation (3.5)

(3.10)

The integral is calculable in closed form; the result is

(3.11)

The asymptotic limits and just introduced in (3.7) make compliant with a minimum condition: u and w are indeed physical boundaries, whereas and are asymptotic extrapolations of u and w. Calculate then the minimum of I with respect to u; so

(3.12)

yield. Next, replacing w in I one finds according to (3.6)

(3.13)

Hence

(3.14)

whereas the average repulsion energy results to be

(3.15)

By direct substitution of the Equation (3.4) into the Equation (3.13) one finds thus

(3.16)

as it is evident recalling the Equation (3.11). Moreover it also appears that in particular, owing to the definition of, the Equation (3.14) is identical to the Equation (3.10) once putting and, i.e.

(3.17)

this emphasizes that the Equation (3.7) represent range boundaries of Q and, more in general, the statistical meaning of Q in the initial Equation (2.7). In other words actually introduces in (3.5) as average value between all allowed values of repulsion energy physically compatible with the electron configuration of the atom/ion: the experimental ionization energy is averaged between asymptotic hydrogenlike properties with negligible interaction between electrons apart each other and asymptotic repulsion interaction so strong for electrons very close each other to balance the binding effect of the nuclear charge; even the probabilistic concept of local electron density is bypassed in this reasoning: according to the positions (2.1), indeed, the lack of any information about implies that the electrons could be anywhere. On the one hand this consideration, which can be verified through the measurable ionization energy, allows to estimate the average repulsion energy as well via the values of and; also, the Equations ((3.14) and (3.15)) show that even is uniquely defined by these values. On the other hand the pertinent Equation (3.17) clarifies the statistical physical meaning of Q in the Equation (2.7), which evidences how to infer the second equation to calculate and via the experimental values of; it is indeed possible to write

(3.18)

The second inequality, self-evident, emphasizes that the problem is now to find couples of different values and compatible with a unique value of for a given electron configuration and selecting among the couples the one consistent with the corresponding minimum: according to Figure 1 and the Equation ((2.7) and (3.1)), indeed, and represent the sought couple of values of Q of electrons. Thus holds the condition

(3.19)

In principle one could try to implement the conditions (3.19) and (3.16) by introducing trail couples of random values and to guess which one best fits the unknown and and fulfills both equations: the physical meaning of this procedure is to reproduce through the values of each trial couple the corresponding conditions of repulsion energy till to find that effectively representing the minimum condition (3.12). This method however, despite its physical compliance with the non-deterministic arrangement of electrons required by the uncertainty (2.1), would be presumably long and unforeseeable from a numerical point of view without a leading criterion to choose the couples. An alternative analytical approach appears necessary. Consider that the Equation (3.19) identifies the specific values and fulfilling by definition the condition (3.12) of minimum repulsion energy of a given electron configuration, whereas instead and imply in general any possible repulsion energy to which corresponds pertinent values. This suggests to find an appropriate variable parameter linking and as a function of which is identified in particular that consistent with the minimum condition for and. This approach has in fact physical valence: it describes the ability of the system of electrons to attain the configuration energetically most favorable for the stability of the atom/ion.

Note in this respect that of the Equation (3.2) is uniquely defined by a given value of the product regardless of the individual values of and; in other words, it is possible to replace with thus regarding the former as a particular case of the latter. This allows generating and examining various values defined by among which to identify the correct experimental value of compliant with (3.12). Moreover, since and are linked by the condition (3.16), it is reasonable to expect that even and do analogously so; it is clear indeed that

(3.20)

i.e. and fulfill the Equation (3.4) because in principle does not depend on according to the Equation (3.1). This holds even for the sum of and corresponding to, whatever their separate values and itself might be. Moreover implement the reasonable positions

(3.21)

where g is an arbitrary variable parameter that turns the true values of Q fixed by the experimental value of into the variables related to. Replace with in the eq (3.19), which thus in general is no longer fulfilled, and multiply all terms by; so one defines a function that reads

(3.22)

and yields eventually

(3.23)

Of course for and, in which case the Equation (3.22) reduces to the (3.19); thus the former is the sought generalization of the latter. Indeed F represents in general any value of repulsion energy in the atom related to any possible random distance between electrons, whereas the zeros of F represent instead the condition of minimum repulsion energy between electrons in a given configuration.

In conclusion, the product of the Equation (3.2) has been rewritten via the arbitrary parameter g, whose change enables to reproduce corresponding values of resulting from the random arrangement of electrons interacting according to the Equations ((3.6) and (3.15)). From a mathematical point of view the Equation (3.22) introduces the second equation additional to (3.4) necessary to find and.

4. Preliminary Calculations

This section highlights in detail how to implement the considerations so far exposed, in particular the Equation (3.22). The experimental values of ionization energy reported in the literature are numbered as for the first outer electron of the shell of neutral atom with Z electrons, for the second electron of the ion with one positive charge and electrons, and so on. In an atom of atomic number Z, the number of residual electrons after ionizations is clearly. Yet, is more significant for the model the relationship between electrons already removed and the number representing the actual electron configuration from which a further electron is to be removed; in effect the ionization energy measures the binding energy of this electron interacting with all electrons. Hence let be: for example the first ionization concerns in the ground configuration of neutral atom, i.e.; so implies, i.e. according to the “Aufbau” rule the principal quantum number is that of the Z-th electron in the whole shell required by the Pauli principle. Instead the last Z-th ionization energy, i.e., implies as it concerns the ground configuration of hydrogenlike ion characterized obviously by to calculate the hydrogenlike energy.

The first numerical example is carried out in particular for and, where implies the second ionization energy of Mn; in this case the electron to be removed is one among those in a shell of 24 electrons. The input data are thus, according to the Equation (3.16) and Figure 1,

(4.1)

moreover the Equations ((3.8) and (3.9)) imply the following ranges and allowed for and

As previously emphasized, and range boundaries are calculable regard- less of any assumption on and, so the positions (4.1) and (4.2) are effectively input data. Now, for clarity and gradualness of exposition, is preliminarily regarded as a known quantity too, calculated from the pertinent experimental value 15.63999 eV of ionization energy [19] . So, owing to the Equations (2.7) and (2.9) it is possible to write

(4.3)

As concerns the number of decimal places in these introductory steps of calculations, note that the Equaiton (2.7) yields

(4.4)

in the present example, calculating with and the quantity in parenthesis, shows that even a small error in estimating implies large error on. Hence the necessity of very small requires accurate estimate of and thus the quoted decimal places reported in (4.1) and (4.3).

Write the Equaiton (3.22) as explicit function of according to the Equaiton (3.21)

(4.5)

the plot of the Equaiton (4.5) vs g, with known, is reported in Figure 2. The direct solution of this equation with respect to g yields four values

(4.6)

to which correspond four values of; the notations will be clear soon below. As expected, F admits the solution. Waiving the negative solution, which is clearly outside the ranges fixed by the Equations ((3.8) and (3.9)), remain three values of useful to calculate as many and respective ionization energies via the Equation (3.23). Note now that the condition posed by the Equations ((3.16) and (3.17)) requires that two among the must correspond to or and to; moreover, the former two must fall in the allowed ranges evidenced by Figure 1. As and, it must be true that, whereas yields of course just itself according to (3.21); instead that yields has no physical interest, because the resulting corresponds to a value of outside both allowed ranges indicated in (4.2). These considerations clarify that the notation “n” stands for negative, “s” for sum, “q” for and “u” for unphysical value of. In conclusion

(4.7)

yield the sought value of that by definition determines the correct value of according to the Equation (4.3).

Note that despite four solutions are provided by the Equaiton (4.5), two of them only are physically valid, in agreement with the two positions (3.21).

These steps and their conclusions suggest the way of generalizing the Equation (3.22) while skipping the necessity of preliminary knowledge of, which is actually the sought parameter as a function of which is inferable. It is enough to examine the Equation (4.5) when takes an arbitrary set of test values, , still in either allowed range of Figure 1; the results then will show themselves which one among the corresponding range of is physically significant.

For clarity it is useful to remark: is a physical parameter describing the change of the related corresponding to different space arrangements of the electrons within the whole shell around the nucleus, to which correspond the resulting values of repulsion energy; is a free numerical parameter aimed to identify which value of, now regarded as unknown in its allowed range, is appropriate to make the solutions of the Equation (4.5) numerically compliant with of the Equation (4.1).

Being g arbitrary, and are independent variables, both subjected however to vary within either allowed interval (4.2); only so they are referable to or at the end of the calculations. Also this point is highlighted by a numerical example.

In fact, the calculation of the Equation (4.5) is identical to that already shown, it is simply repeated for all desired test values of to be examined: once assigning arbitrarily various input values of in either interval (4.2), the Equation (4.5) is again solved with respect to g and yields values with physical meaning analogous to that just remarked in (4.6). The results are reported in the Table 1, whose columns show in the order: the test inputs, the three positive solutions analogous to that of the eqs (4.6), the respective values of corresponding to i.e.; next, in analogy with (4.7), are reported and eventually calculated with each input value of. In principle, waiving, unphysical for the reason previously explained, all values of are acceptable; but clearly one row only of the table is correct, the one fulfilling the condition (3.16). Also now hold identically the considerations leading to the eq (3.20).

Hence, examining Table 1, one concludes uniquely that and are to be accepted among the test values of the first column. In particular it is confirmed that the solutions of the Equation (4.5) imply the key relationship between two of them only

which clarifies the purpose of this preliminary exposition aimed to highlight the physical meaning of the values (4.6): the input is known, the solutions and are calculable for any in the allowed range of Figure 1, the sought is uniquely identified by.

Of course this procedure can be identically applied to any values of and; in this respect a further example is worth being reported in Table 2 to ensure that the agreement just found in Table 1 is not accidental. This table is understood exactly as the former one as concerns the necessity of considering again the specific that yields the correct value of ionization energy, despite a different set of test input values deliberately introduced to confirm that the particular choice of the input values of the first column is effectively arbitrary and irrelevant.

It is worth noticing that the exact coincidence between one of the calculated and the required is actually obtained because the arbitrary inputs have been purposely introduced in order to include in particular also the value coincident with the actual; this aims to evidence that just this latter test value, and this latter only, fulfills the required boundary conditions (3.16) and (3.17). In practice the inputs in the first column have not been randomly defined, but calculated for mere numerical purposes as, with of course arbitrary and progressively increasing but optionally including too. In fact, from a calculation point of view, this is a mere shortcut to avoid trivial numeric procedures, e.g. interpolation between contiguous or best fit calculations and so on to include and identify the

key condition. Clearly the present procedure is preferable to introduce explicitly also the correct input that identifies directly, without ambiguity due to mere numerical interpolation approximations, just the required result among the various inputs.

What is really crucial, indeed, is that in the first column of Table 1 and Table 2 there is no conceptual reference to anything explicitly or implicitly referable to the true value: this latter is simply “hidden” in the first column until the mere comparison between the known and calculated from the various reveals the true physical identity of the correct input test value.

Actually there is a more substantial physical reason to propose such a calculation strategy. In the present model the repulsion energy (3.6) is quantized; i.e. not only but also are calculable through the same and identified as shown above and through n. Both are actually eigenvalues; in fact the specific value of n is implemented to calculate the values of Table 1 and Table 2 according to the “Aufbau” criterion, as it appears in the list of input values (4.1). Hence n, appearing in the early Equation (3.1) as a consequence of (2.1), could take in principle arbitrary integer values higher than that required by the Pauli “Aufbau” defining the ground energy levels. On the one hand the calculated can only take discrete values contributing to the respective, discrete as well of course; on the other hand the experimental values of ionization energies are in practice exact values, they are measured with the accuracy of several decimal places.

These statements merged together allow two alternatives only: either the model provides exact values for the ground state of atoms/ions or the model is wrong.

To verify this conclusion Table 3 and Table 4 extend the outcomes of such calculations for all electron configurations from to for various atomic numbers Z initially selected to verify correctness and reliability of the model: have been examined (S), (Cl), (Ar), (K), (Ga) and (Mn) and all of their ions implementing anyway “Aufbau” input values of n. These tables are significant because they exemplify the cases of non-metal, gas, noble gas and metal elements. In all cases the calculated results coincide with the experimental values reported in the literature: the monotonous repetition of identical calculated and experimental values relies on the reasoning based on the discreteness of allowed values just exposed. Is in particular important the case of Mn for the reasons better emphasized in the next section.

5. The Transition Elements

This section concerns the central point of the present paper, i.e. the calculation of the ionization energies of the TE. Table 1 and Table 2 and Figure 2 aimed essentially to highlight the method of calculation, whereas the six atoms/ions of Table 3 and Table 4 are enough to verify the generality of the results achievable with the conceptual frame highlighted in the section 2. The previous examples have deliberately concerned chemical elements whose electron pile-up follows the mere Pauli principle, although it is not so for K, Ca and Mn, whose energy level 4s is lower than 3d; in particular, for the electron configuration

of the neutral atom is, that of a singly ionized state is. As Mn is in the first 3d block, three further elements have been checked before examining lanthanides and actinides: Sc, which still belongs to the first block, and Y and Mo that belong both to the second d block.

The chance of including successfully even these three elements among the test examples stimulates to extend the present analysis of the electron energy levels also to the transition elements of the lanthanide and actinide series. For this reason Table 5 and Table 6 report respectively examples of results calculated for, , and, ,. The ground electron configurations of the elements in Table 7 are: for La, for Ce and for Tb. The electron configurations of the elements in Table 5 are: for Th and for Pa. One element only of the former series is radioactive; all elements of the latter series are radioactive, some of them do not exist in nature. The data available in literature quote some ionization energies only, all reported in the tables; in both cases the elements have been chosen without any special selection criterion, but mostly on the basis of the amount of available experimental data necessary to validate the model as convincingly as possible. These values however are enough to show that the present scheme of calculations fits adequately even these elements and their ions.

As concerns the outcomes of the present model, apparently nothing distinguishes these elements from “regular” elements like Ar with; this holds both for neutral atoms and their ion states. The results confirm what has been verified in Table 3 and Table 4, i.e. even the transition elements fit the general calculation scheme hitherto introduced. The approach systematically implements all numerical steps from the Equations ((3.10) to (4.5)) via, which depends on, and only: one infers therefore as a function of the electron cloud and nuclear charge through the Equation (2.7).

The fact that this calculation scheme holds regardless of the different physico-chemical properties of the atoms/ions has a double explanation. On the

one hand, as previously explained, and govern entirely, and thus the energy levels; as by definition, it is immediate to calculate all starting from the first non-relativistic hydrogenlike level or Dirac relativistic level that appears here as a mere additive term. On the other hand, this means that Q of the Equation (2.7) includes and somehow summarizes all physical effects underlying not only the mutual repulsion between electrons but also relativistic effects like their spin-orbit or spin-spin interaction. The next section aims to highlight these crucial points.

6. Discussion

The horizon of the present model is the whole periodic table of the elements, not some specific electron configuration of selected atoms/ions. Further calculations, not reported here for brevity but easily executable because of very short computation times, show that the same agreement holds for all ionization energies of all atoms. In the present model two constants only are predetermined, the universal values of a and b of the Equation (2,7); indeed and, early introduced in [17] as best fit constants for each electron configuration, are calculated here in agreement with the values determinable via the experimental value of the ionization energy through the Equation (3.1).

The considerations hitherto introduced waive the usual concepts of Schrödinger equation and wave function. The fact that the wave mechanics regards the transition elements as having an anomalous filling of orbitals characterized by progressive quantum numbers is not surprising; the standard quantum mechanical calculations in general implement wave functions that imply four quantum numbers including the spin. Hence, when examining the ground quantum states of isolated atoms/ions described by n, l, m and s in the absence of external fields, the relative energies of the respective orbitals govern the occupancy electron states and their correlation. Yet, according to the basic ideas hitherto exposed, the TE do not represent any anomaly; reasonably this is because the concept of orbital is waived in the present model, which is much more agnostic than the wave mechanics itself and just for reason more essential and simpler. A few elementary considerations replace the considerable mathe- matical difficulty of handling systems of tens of interacting electrons. The Equation (2.1) skip even the probabilistic meaning of orbital, while compelling to accept total lack of information about all local dynamical variables; never- theless, the outcomes of the section 2 are completely analogous to that inferred solving the corresponding wave equations of the wave mechanics. Also, the approach based on the space time quantum uncertainty actually regards n as a number of allowed quantum states; it plays a role analogous to that of the principal quantum number, but probably this analogy cannot be further extrapolated.

This point deserves attention. More specifically, let the ground state of a given TE be that with preferential filling of the orbital instead of the orbital: the incomplete filling of this latter is in fact the typical case of the first and second transition metal series. If the preferential occupancy of the orbitals and is assessed comparing the energy of the electron in either of them, one concludes that the key parameter discriminating either chance is the correlation energy. This conclusion however does not contradict the fact that, according to the Pauli principle, the number of electrons com- patible with a given quantum number n is anyway. Just this is the key point of the present model, which conceptually introduces n as a number of allowed quantum states and not as a quantum number resulting from the solution of the Hamiltonian; in the section 2 there is indeed no reference to any wave equation. As l and s do not appear explicitly in this model, rather both simply contribute to the values of and controlling, there is no reason to expect that the Equation (2.1) give results still affected by the constrains due to the corre- lation condition on either orbital energy; in other words, instead of calculating explicitly the correlation energy the previous considerations aimed to calculate correctly the related values of and.

To understand why the standard approach based on the wave equation conflicts with the regular “Aufbau”, it is enough to emphasize that the Equation (2.1) are inherently rooted in the fundamental concept of space time as shown in [20] ; the wave formalism, inferred from the (2.1) as a corollary [21] , represents the chance of extracting the probabilistic essence of the wave mechanics from the total agnosticism of the quantum uncertainty. The postulates (2.4) and (2.5) of the wave mechanics are actually straightforward corollaries of the (2.1); for this reason the wave chance implies as a matter of fact a more difficult mathe- matical approach. In effect the Equation (2.7) was obtained in [17] from the (2.1) only, as shortly summarized in the section 2 to make this paper as self contained as possible. This suggests that the anomalous way of filling the energy levels is actually necessary and appropriate to make the quantum mechanical wave formalism compatible with that, more general, implementing directly the total uncertainty. Accordingly, once having bypassed the wave function from which the energy operator extracts the energy eigenvalues, it is rationale that the order of progressive orbital filling becomes bypassed as well; the Equations ((3.8) and (3.9)) in effect regard every electron identically at infinity or very close each other regardless of any probabilistic constrain, i.e. without any orbital occupancy sequence. Note that these considerations have been proven valid also for the diatomic molecules and, mostly important, are susceptible of relativistic gene- ralization. The remainder of the paper aims to explain further just these crucial points. Two facts deserve attention:

1) the principal number n of allowed quantum states only has been here implemented;

2) the systematic coincidence between calculated and experimental ionization energies implements the “Aufbau” principle only, see inputs (4.1).

This is because all calculations concern essentially Q initially introduced in the Equation (2.7) and subsequently inferred from the experimental values of in the Equation (3.1). On the one hand, the results support the validity of the Equations ((2.7) and (3.22)), i.e. the Equation (3.11) behind them; on the other hand, the fact that the way of calculating Q in Table 1 and Table 2 reproduces just the value preliminarily inferred from, suggests how to regard the theoretical approach itself. Clearly and have relevant physical meaning as concerns the electron energy levels of atoms and ions; these quantities, having statistical meaning, include and summarize all physical effects drastically affecting the electron energy levels, Equation (4.4). So it is reasonable, rather than paradoxical, the fact that once having implemented n only, which somehow surrogates the principal quantum number in the Bohr atom, the present outcomes skip any consideration about l and s and the quantum energies of the related orbitals. The Pauli “Aufbau” is appropriate and enough. Moreover an unavoidable consequence of this reasoning also involves the link between non-relativistic and relativistic approach, which is expectedly relevant for high Z elements and thus inherently implied itself.

Regard for the moment Q as an empirical quantity directly inferable from experimental measurements, regardless of how the model calculates it and even irrespective of the validity of the Equation (2.7) itself; as such it necessarily includes all possible effects concurring to the ultimate value of, whatever the physical nature of these effects might be. From this standpoint, one could think that a non-relativistic value preliminarily introduced could lead to an approximate, after which appropriate considerations could lead to Q taking into account all necessary relativistic corrections. However, the reasoning carried out in this paper does not attempt, even preliminarily, such a legitimate strategy; rather the approach has introduced first the actual values of Q via the experimental, and then has described the theoretical path to infer it simply fulfilling the boundary conditions (3.16) and (3.17). The way to calculate Q does not imply special hypotheses valid for particular elements, it includes light and heavy nuclei. Actually, the Equation (3.22) exploits the mere fact that two values of Q are compliant with a unique value of because the Equation (2.7) is an elementary second degree equation; the Equation (3.22) simply equates two different ways, see Equation (3.19), to express and. For this reason the model skips any hypothetical and bypasses the peculiar wave functions of the TE as concerns the standard principle of the Pauli “Aufbau”: once having implemented the number n of allowed quantum states only, the TE appear as “regular” atoms/ions i.e. no reason compels regarding them differently from other “standard” elements. Strictly speaking, the initial Equation (2.7) is legitimated not only by the fact of being direct consequence of the Equation (2.1), which imply the correct consequences shortly concerned in the section 2, but also on the fact of having introduced a general physical criterion to calculate and without “ad hoc” hypotheses: in a certain sense, just the simplicity of the reasoning in the section 4 supports the Equation (2.7), rather than vice versa. In other words: any alternative function, true or wrong, could anyway imply in principle two values of Q related to; however, this hypothetical function should be legitimated by a valid and general reasoning to infer Q, without which it is a mere mathematical function unphysical and thus worthless. In this respect, apart from the ability of finding sensible results of, the present model also implies in a natural way quantized correlation energy: in effect it is physically inappropriate to think that continuous values of the related correlation terms, whatever they might be, are compatible with the discrete electron energy levels experimentally revealed by the spectral lines of atoms and ions. Also this point has been checked considering of course the Equation (3.15) that fulfills the minimum condition (3.13), and not the preliminary eq (3,6). Calculate thus the Equation (3.15) putting n equal to the “regular Aufbau” quantum number and owing to the Equations ((3.17) and (3.16)) expressing the average condition of minimum repulsion energy. Expectedly the values of should exhibit some form of regularity appearing when expressed for any as a function of Z. Figure 3 reports and as a function of the atomic number for all elements from in the former case and in the latter case to. The plot has been determined using deliberately either Q calculated from the experimental values of to show that the resulting plot has the expected regularity even for elements not appearing in Tables 1-6; in this case the plot represents actual experimental data and thus verifies the validity of the Equation (3.15). The discontinuities are found in correspondence to the change of n for Z consistent with the corresponding electron shell of neutral atoms and the required “Aufbau” n. For this reason the experimental is particularly significant: it shows that the discontinuities occur for Z to which correspond jumps of n of the electron shell.

The quantization of repulsion energy has an interesting consequence as concerns the space arrangement of the electrons in a shell: the energy of this arrangement should be regarded not as that of a mere “gas” of electrons randomly distributed around the nucleus, in which case the electron correlation energy could statistically take any value, but rather as a sort of regular local structure characterized by well-defined average energies of its ground and excited states. Indeed, owing to the Equations ((3.14) and (3.15)), the plot of fig 3 has been calculated with to describe the ground state of the atoms/ions; yet, in principle, it could be also calculated with any thus describing excited states of repulsion energy and ionization energy. In effect such conclusion agrees with the results of an empirical model based on a significant number of experimental ionization energies [22] .

At this point an interesting question arises: apart from the merit of bypassing hard mathematical difficulties, do really the Equation (2.1) have inherent relativistic valence? The allusion to the relativity is unavoidable even in the present context: the spin is a relativistic property, introduced by Dirac in his seminal model of relativistic atom via new specific operators called “spinors”. It seems doubtful to obtain correct values of energy levels for heavy elements without considering topics like spin-orbit or spin-spin interactions, which imply the Lamb shift too, in the frame of a simple theoretical approach like that hitherto exposed. Also: why in the Equation (2.6) the hydrogenlike energy levels are expressed as a function of quantities like and that are typically relativistic and merge relativity and quantization via n without having introduced purposely relativistic concepts? Since the present model is based on the Equation (2.1) and their implications, the starting Equation (2.7) is in fact a direct corollary, it is necessary to highlight what the Equation (2.6) and the Equation (2.1) themselves have to do with the relativity.

In short, these questions are all summarized in the following one: why should be the Equation (2.1) really far reaching?

Despite an exhaustive answer to these questions is outside the purposes of the present paper, it is necessary to remind that the so called “relativistic effects” actually are themselves nothing else but quantum effects; the paper [21] has shown indeed that even the general relativity is rooted into the Equation (2.1) and that the wave operator formalism is a corollary itself of the Equation (2.1). Moreover even the quantum fluctuations of the black body imply by conse- quence relativistic corollaries [23] as well. These points, crucial to complete and justify the previous considerations of the section 2, deserve being very shortly sketched below although more specifically concerned in several dedicated papers. Mostly important, no additional hypothesis is necessary to this purpose: considering for simplicity and brevity the moduli of the momentum and velocity vectors, are evident some straightforward consequences implied by the considerations of the section 2.

i) First of all, the Equation (2.1) merge in a natural way space and time coordinates. Moreover note that the Bohr radius is inversely proportional to m. Reasoning in terms of local coordinates, this statement is self aimed: it concerns two particles more or less apart each other. The implication is different considering the Equation (2.2) that concerns instead the space time range size; the same formula expressed as a function of instead of the local distance r means that the space time is affected itself by m, i.e. the higher the mass the stronger its shrinking effect on the space time size. It is reasonable to guess that this effect has to do with the local space time curvature induced by the presence of a mass, one of the most relevant ideas of the general relativity together with the constancy of light speed.

ii) As concerns just this second statement, let us show how it explains the Equation (2.6). Consider that the Equation (2.1) read identically

(6.1)

and also imply for any random and unknown local values and within the respective uncertainty ranges and. In other words: in the section 2 the positions and aimed to replace the local dynamical variables with uncertainty ranges fulfilling the Heisenberg principle, here we say that and imply by definition the random local variables and. Multiplying side by side and the first (6.1) one finds, i.e. and therefore for the random local dynamical variables and. Note that this last result is consistent with the definition, being q an appropriate parameter; indeed eliminating v from this position and (6.1) one finds i.e. and thus again. While is in principle any square velocity by dimensional reasons, has particular interest the case where v takes a peculiar physical property: calling c this special value of constant velocity, necessarily finite and invariant by definition, the position, in principle possible because no preliminary hypothesis has been made on v and q, implies further physical information: expressing in explicit form without loss of generality and one finds and eventually. Despite all local dynamical variables are random and unknown according to the quantum uncertainty, these results read in general

(6.2)

the constant is determined defining a new quantity m as

i.e. by dimensional reasons; is the limit value of of a particle at rest in a given reference system. Hence the peculiar property of c allowing all of this is its constancy and thus its invariance by definition. The former two equations, well known, imply the Lorentz factor and the concept of rest mass m; moreover, if the aforementioned peculiar property of is the invariance of c, the related concepts of relativistic invariance in two inertial reference systems of the Equation (6.2) are so evident that three comments are straightforward:

-These results clarify why the Equations ((2.3) and (2.6)) show that all of this has to do with the quantum energy and its link with and via.

-Note that and of the standard special relativity are ranges exactly known; here instead they are uncertainty ranges, whereas and are local dynamical variables random, unknown and unknowable and thus of no interest. However, the formulas and the concept of invariance are the same.

-The standard relativistic metric unavoidably leads to the existence of three components of angular momentum [24] , whereas the dynamical variables and calculated with the tensor formalism are clearly incompatible with the Heisenberg principle. Starting from the Equation (2.1), instead, everything fits both quantum and relativistic principles; indeed it is easy to show that even the equivalence principle of the general relativity and its consequences are found as straightforward corollaries. It is immediate to show that the metric follows itself from the uncertainty implementing the Equation (6.2) exactly as done in the section 2. Regarding and as local values included in the respective uncertainty ranges (2.1) and replacing them with these ranges, the Equation (6.2) reads. Hence the Equation (6.2) turn into

which reads i.e.

(6.3)

clearly F represents force. There are at this point two chances, i.e. F could be in principle constant or not. In the former case with the right hand side of the first Eq. (6.3) reads; i.e. the Equation (6.3) reduces to the well known invariant interval of the special relativity, being m by definition an invariant free parameter. As shown in section 2, however, this metric is clearly consistent with the Heisenberg principle and one component of only, as it must be.

If F is not constant, it is easy to infer from the (6.3) the space time metric of the general relativity; the reasoning closely follows that exposed in [23] .

This shows that the positions and replacing the usual and and implemented in the section 2 to convert the classical angular momentum and energy into the respective quantized equations are also valuable to infer relativistic information from the random local variables.

iii) The following considerations show how to infer the concept of spin directly from the Equation (2.1), simply implementing the fact that uncertainty regards the quantum numbers as numbers of allowed quantum states. Start from the non-relativistic square quantum momentum inferred in the section 2

(6.4)

Rewrite identically the first equation as, whence

(6.5)

after having added at both sides of (6.4). Trough this trivial manipulation the initial turns into a new angular momentum, whose square modulus defined at the left hand side is equivalently rewritten at the right hand side. Note now that, being an arbitrary integer including 0, it is possible to write; clearly it must be too. Then put being. Also note that includes itself the possible value 0 and that and are by definition independent addends of the arbitrary; therefore they can take in general independent values, so that it is possible to write

(6.6)

It is clear now the notation: refers to the unique component knowable of the orbital angular momentum, is a new kind of angular momentum. Moreover, being arbitrary, it is possible that although. Hence cannot have kinetic meaning, i.e. it must intrinsically belong to the particle regardless of its state of motion.

In conclusion, one could say elementarily that the component of a half-integer angular momentum component must exist: not because the micro-magnet behavior of the electron is necessary to explain the Stark and Zeeman splittings, but because it is straightforward implication of the mere quantization itself.

The fact that coexist both Equations ((6.4) and (6.6)) suggests that integer and half-integer forms of angular momentum exist in the nature with s both integer or half integer, being the former a particular case of the latter for.

On the one hand, this conclusion agrees with (6.5), i.e. J has a more general physical meaning than and; on the other hand, the chance that even though suggests that must be an intrinsic property of particles regardless of their state of motion, i.e. all particles are characterized by their own integer or half integer. In many electron atoms it is possible to write i.e. and, where counts the number of electrons contributing to the total angular momentum, so that are both acceptable forms. These ways of rewriting are not merely formal: the sum could regard an arbitrary number as sum of arbitrary and or as a sum of addends. These remarks are the key to infer the Pauli principle about the occupancy of quantum states: it is also immediate to realize why the spin implies two different ways to fill the quantum states, simply considering that both and defining are arbitrary. Also this point, concerned in detail in [20] , is shortly summarized here for completeness.

Let and refer to any integer spin particles 1 and 2; then does not allow counting how many particles 1 and 2 contribute to. Since and particles of this kind yield, it is impossible to discriminate whether is the value of of one particle only, or it is due to of quantum particles. As concerns, the total quantum states of systems of one particle or particles are indistinguishable because actually and and are indistinguishable integers themselves. Repeating this reasoning for half integer spin particles is impossible, because adding one new particle to a given system of particles means jumping from integer to half integer to integer total angular momentum of spin. The total quantum state is no longer indistinguishable with respect to the number of particles, i.e. it is sensitive of the addition of new particles, i.e. each new particle determines a requires its own quantum state distinguishable from the previous one. This is nothing else but a different formulation of the Pauli principle.

iv) Consider now the Equation (2.3) and note that is defined by two factors, m and fundamental constants. It has been written in the chain of Equation (2.6) as a function of or through the energies or: the former does not necessarily depend explicitly on m, as p can describe even a wave of wavelength, the latter does. This suggests the chance of examining more systematically how can be related to various forms of energy according to various powers of. The results of this elementary analysis is summarized as follows

All of these formulas, written for simplicity and brevity in scalar form, are well known; what is interesting is that are all obtained from the energy characterizing via different powers of the fine structure. The rest energy has been introduced in the point (ii). A few and elementary considerations merge quantum and relativistic physics.

With the help of and Compton length one finds the basic definitions of electric and magnetic fields; even the Bohr magneton is definable as via the coefficient 1/2 present in all formulas.

In summary the first formula shows the particle nature of the electron besides its wave behavior evidenced by the Equations ((2.4) and (2.5)) in a unique conceptual frame rooted on the Equation (2,1) only. The second and third formulas show its electric and magnetic properties of the electrons, which suggest the well known Stark and Zeeman effects.

It is remarkable that all energies at right hand sides of these equations, including the relativistic and related, are actually linked to via and number of allowed quantum states: the relativistic forms inferred from the metrics consider instead only.

As a final remark, note that in principle nothing hinders to extend the present approach to calculate also ionization energies and energy levels of atoms/ions in condensed phases. Whatever the pertinent might be, indeed, the fact that the Equation (2.7) is direct corollary of the uncertainty Equation (2.1) suggests that a generalized function of the Equation (2.7) having the form can be reasonably defined; this form simply introduces the idea that includes now also the interaction energy of the electron shells of any atom/ion with that of the surroundings, e.g. in a crystal lattice. Clearly the idea of minimizing the perturbation induced by first neighbors on the electron system of a given atom/ion still holds, provided that it includes too; in principle the key steps of this generalization should be therefore still similar to that of the Equations ((3.10) to (3.18)), but including an additive average term. Once having acknowledged that the number of electrons in a shell does not imply computational problems, why to exclude the chance of describing even the interaction between contiguous shells? Work is in progress on this point.

7. Conclusions

The present model, purposely aimed to calculate ionization energies, has also shown straightforward implications involving in a natural way even the relativity, inferred contextually to the concept of quantization of the energy levels. These short notes, fully discussed elsewhere, have been summarized simply to elucidate the elementary, straightforward and tight link between quantum uncertainty and special relativity. An elementary extension of these considerations leads to relevant results of general relativity [21] . This helps to understand why the approach implementing uniquely the Equation (2.1) is in principle more complete and profoundly rooted on the most fundamental principles of nature than the wave operator formalism.

On the one hand, the simplicity of the approach evidences itself the direct connection between quantum uncertainty and “Aufbau” principle; on the other hand, the fact that the average repulsion energy is quantized itself, as shown in Figure 3, helps to better understand the concept of correlation. It seems oversimplified the idea of electrons merely repelling each other in a shell, without considering also that the energies of a given configuration can take allowed values only.

The quantization of energy levels results from that of the hydrogenlike term and that of the mutual interaction. Strictly speaking, there is no reason to expect that the attractive electric interaction with the nucleus only leads to discrete energy levels, whereas instead the repulsive electric interaction between electrons should not. Rather it seems more rationale to think that the orbitals are modified by the electron correlation in order to fulfill two quantized effects, and thus that the standard way of implementing the “Aufbau” for the Bohr quantization alone is incomplete; as such, in principle it fails like any partially valid assumption.

Cite this paper

Tosto, S. (2017) Many Electron Atoms: Ionization Energies of Transition Elements. Open Journal of Physical Chemistry, 7, 89-121. https://doi.org/10.4236/ojpc.2017.73007

References