Open Journal of Physical Chemistry
Vol.05 No.03(2015), Article ID:58337,6 pages
10.4236/ojpc.2015.53006
Simulation of 5-Fluorouracil Intercalated into Montmorillonite Using Spartan ’14: Molecular Mechanics, PM3, and Hartree-Fock
John H. Summerfield
Department of Chemistry and Physical Sciences, Missouri Southern State University, Joplin, USA
Email: summerfield-j@mssu.edu
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 9 June 2015; accepted 25 July 2015; published 28 July 2015
ABSTRACT
Molecular mechanics calculations, based on equations such as the one below, are used to investigate a colorectal cancer drug, 5-fluorouracil, intercalated into a clay, montmorillonite. This combination is currently being considered as a drug delivery system. The swelling of clays has been studied since the 1930s and is still not fully understood. Spartan ’14 is used for the calculations. Semi-empirical and ab initio basis set scaling is also examined since there are roughly 300 atoms involved in the full model.
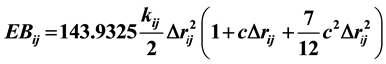
Keywords:
Quantum Chemistry, Clays, Spartan ’14

1. Introduction
Colorectal cancer is expected to cause 50,000 deaths in the US in 2015 [1] . Surgery is typically the first option. If the disease is more advanced chemotherapy is relied on. The major alternative to chemotherapy is the drug 5-fluorouracil [2] . This drug is shown in Figure 1.
The objective of this work is to correctly model 5-fluoruracil as a pillared molecule between montmorillonite layers. The novelty of this study is to evaluate Spartan ’14’s ability to carry out this plan. In this regard molecular
Figure 1. 5-fluorouracil. The carbons are gray. The oxygens are red. The nitrogens are blue. The fluorine is yellow. The hydrogens are white.
mechanics, semi-empirical, and Hartree-Fock computational approaches have been used to calculate the optimized structure of 5-fluorouracil intercalated between the layers of montmorillonite, a possible drug carrier.
Soils are typically 50% minerals by volume. Oxygen and silicon make up about 90% of this volume. For example, two common minerals are olivine (Fe2SiO4) and beryl (Be3Al2Si6O18).
Many soil minerals exist as sheets of repeating units. One type of these minerals is the phyllosilicates [3] . Phyllo is from the Greek word for “leaf”. Not surprisingly, mica is a phyllosilicate. Mica is shown in Figure 2.
Phyllosilicates are divided into two types, 1:1 and 2:1 minerals. These ratios refer to how the sheets are arranged. Phyllosilicates consist of sheets of polymerized SO4 tetrahedra. They are bound at three oxygen sites. The sheets are weakly bound by van der Waals forces. In addition to the tetrahedra, phyllosilicates have a sheet of octahedra (elements in six-fold coordination by oxygen) that balance out the basic tetrahedra, which have a negative charge. These tetrahedra and octahedra sheets are stacked in a variety of combinations to create the phyllosilicates. Clay minerals are a group of hydrous phyllosilicates characterized by sheets of corner sharing SiO4 tetrahedra and/or AlO4 octahedra [2] .
The 1:1 layer structure consists of one tetrahedral sheet and one octahedral sheet as the repeating unit. An example of a 1:1 clay is kaolinite [4] . Kaolinite is shown in Figure 3.
Montmorillonite is an example of a 2:1 clay. It consists of two tetrahedral sheets sandwiching an octahedral sheet. Montmorillonite’s structure is shown in Figure 4 along with five intercalated 5-fluorouracil molecules.
Only oxides are present in these model molecules, no hydroxides. The distance from the top of one layer to the top of the other―the basal spacing―is 4.8 × 10−10 m in oven dried montmorillonite and 9.6 - 10.0 × 10−10 m in the hydrated structure [5] . There are five 5-fluorouracil molecules intercalated between the layers so the interlayer distance is 12.5 × 10−10 m.
On closer examination of Figure 4, montmorillonite’s tetrahedral sheets consist of [SiO4]4− anions and the octahedral sheets of [AlO3(OH)3]6− anions. The isomorphous substitution of Al3+ with Mg2+ or Fe2+ in the octahedral sheets or replacement of Si4+ with Al3+ in the tetrahedral sheets generates a surface with negative charge. In nature, sodium, calcium, or magnesium intercalates the sheets to balance the charge. For 5-fluorouracil to displace the metal cations, it must form stronger intermolecular attractions than the cations [6] . Mica differs from montmorillonite. In mica, some of the silicons are replaced with aluminum. Ideally, every fourth silicon is replaced.
Currently montmorillonite is considered a good host material for controlled drug delivery. Controlled drug delivery has been of interest as a method of effective and targeted drug delivery as well as a method to reduce side effects. Particular attention has been paid to find a way to regulate the rate of drug release by a carrier where the drug is dispersed or incorporated in an inert matrix. To develop such carriers the interaction between the host (clay) and the guest (drug) compound has been of interest. It is important that the host material is harmless to the human body, will disintegrate, and be eliminated from the body once its drug delivery job is over. Due to flexible interlayer space, montmorillonite is a very good host for many guest molecules [7] .
Clays were first ingested for their healing powers, medicinal effects, and as ceremonial offerings. The consumption of clays for antidiarrheal purposes has been known since the 1800s. The Chimayo clays of New Mexico
Figure 2. Mica. Silicon atoms are gray. Oxygen atoms are red. Aluminum atoms are pink. Magnesium atoms are violet.
Figure 3. Kaolinite. Silicon atoms are gray. Oxygen atoms are red. Aluminum atoms are pink.
Figure 4. Montmorillonite’s molecular structure along with five 5-fluorouracils. It consists of one octahedral sheet and two tetrahedral sheets. The hydroxides form at higher pH values while oxides are present at lower values. Oxygens are red. Silicons are gray. Aluminums are violet. Magnesiums are pink. Fluorines are yellow.
has been used for healing for so many years that the town’s church is lined with abandoned crutches in testament to the medicinal value of this clay [8] .
Montmorillonite has been shown to absorb a neutral base and then catalyze the base’s conversion to its conjugate acid [9] . This reaction can be seen as another indication of the special quality of montmorillonite’s surface.
2. Molecular Mechanics
Because of the combination of compositional disorder and the variety of stacking arrangements of the layers, complete information on the structural details of intercalated montmorillonite cannot usually be found using X-ray diffraction. Also, although a great deal of knowledge has been generated by various spectroscopic methods, such as infrared, these results typically require a degree of interpretation so are seldom unambiguous.
Force fields based on classical mechanics are a cornerstone in modern drug design. Molecular mechanic force fields have been used to calculate molecular geometries, energies, and thermodynamic properties [10] [11] .
To begin, this work relies on the MMFF94 parameters [12] [13] as they are incorporated into Spartan ’14 [14] . MMFF94 relies on seven energy terms. The energy expression includes a term for bond stretching, angle bending, stretch-bend interactions, out-of-plane bending, torsion interactions, van der Waals interactions, and electrostatic interactions.
The bond stretching energy expression is in the Abstract. In this expression
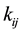 is the force constant between the associated MMFF94 atom types. An example of an atom type is a C-N amide. This atom type has a calculated force constant of 5410 kJ/mol・Å2. It is based on methylformamide and the Morse potential. The
is the force constant between the associated MMFF94 atom types. An example of an atom type is a C-N amide. This atom type has a calculated force constant of 5410 kJ/mol・Å2. It is based on methylformamide and the Morse potential. The
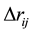 term is the difference between the actual and the associated MMFF94 atom type bond lengths, and c = −2 Å−1 is the cubic-stretch constant.
term is the difference between the actual and the associated MMFF94 atom type bond lengths, and c = −2 Å−1 is the cubic-stretch constant.
Molecular mechanics calculations are much faster than ab initio methods. Molecular mechanics calculations are so fast because instead of matrix diagonalization, a sum of terms is used to describe each atom. That is, individual electrons are not described but rather each atom and its electrons are units that are interconnected by the MMFF94 functions.
3. Molecular Mechanics Model Results
Figure 5 shows the swelling of the clay due to increased number of 5-fluorouracil molecules. Similar behavior is seen with a zinc intercalation simulation [15] . The interlayer spacing is on par with hydration simulations [16] [17] .
Molecular mechanics calculations treats the rigid 5-fluorouracil as though it was a water molecule. That is, the guest molecules slide into the clay and form stacks.
4. Basis Set Methods
It has been shown that rigid molecules form pillars rather than stacks as they intercalate into the clay [18] [19] .
Figure 5. Intercalation of 5-fluorouracil at different interlayer spacings.
A more sophisticated calculation method or fewer atoms is required. More complex calculation methods treat the atoms and their electrons individually. The simplest of these are the semi-empirical methods. For example, parameterized model 3, PM3, uses Slater-type orbitals (STOs) to model the electrons. Each STO has the form
 . (1)
. (1)
where N is the normalization factor, r is the electron-nucleus distance, n is the principle quantum number of the electron, ζ is the effective nuclear charge, and Y(θ, ϕ) describes the angular motion of the electron [20] . Typically a linear combination of STOs is used for each electron used in the calculation. The effective nuclear charge is initially guessed from known molecules so energy minimization occurs quickly.
The problem with STOs is they increase steeply near the nucleus, where the electron-nucleus attraction is greatest. To speed calculations STOs are modelled using better behaved Gaussian functions. Two to twelve Gaussian-type orbitals are combined to model one STO. These two aspects are combined in naming basis sets. The STO-3G basis set relies on three Gaussian function to model each STO. The VSTO basis set only models the valence electrons. The 321-G uses three Gaussian functions for nonvalence electrons, two gaussians for small valence orbitals, and one for large valence orbitals. For example, the valence shell 2 s and 2 p orbitals are split into two pieces: the inner part is the sum of two gaussians while the outer part is modeled by one gaussian [21] .
The next step up in calculation complexity is a Hartree-Fock calculation. In this case no experimental data is relied upon. Instead the effective nuclear charge is varied sequentially until the lowest energy is reached [22] .
5. Basis Set Model Results
At the level of PM3, the current model calls for 1099 basis functions. CPU time scales as n3 or n4 where n is the basis set size [23] . Splitting the difference, this would call for about 10993.5 s of CPU time which is over a million hours. For this reason, the model was reduced from 238 atoms to 58 atoms, about one-fourth the size. The modelled atoms are silicate rings and a 5-fluorouracil molecules. The simplified molecule is shown in Figure 6.
One change caused by simplifying the model is that now the 5-fluorouracil forms a pillar between the clay layers, as supported by experiment. The ground state energies found by different calculation methods are collected in Table 1. The interlayer distance 12 × 10−12 m.
6. Discussion
Spartan ’14 converges for 58 small atoms. It only converges at the Hartree-Fock level using one of the smallest, diffuse basis sets, 3-21G*. This evaluation will hopefully provide guidance for future applications.
This evaluation of Spartan ’14 is a reminder that experiment and computation go hand in hand. When too many molecules are used 5-fluorouracil is modeled as a hydrating molecule rather than a pillared molecule. Apparently, weak, short-range interactions are most important.
One possible extension is to investigate the protonated clay. It is shown in Figure 7 along with one 5-fluorou- racil molecule. This structure would offer the chance to investigate hydrogen bonding between the host and the guest.
7. Discussion
Spartan ’14 easily models the intercalation of 5-fluorouracil into montmorillonite layers at the molecular
Table 1. Ground state energy of 58 atom model relying on a variety of calculations.
Figure 6. Silicate rings and a 5-fluorouracil molecule. Oxygens are red. Silicons are gray. Aluminums are vio- let. Magnesiums are pink. Fluorines are yellow. The interlayer distance 12 × 10−12 m.
Figure 7. Protonated montmorillonite layers and a 5- fluorouracil molecule. Oxygens are red. Silicons are gray. Aluminums are violet. Magnesiums are pink. Fluorines are yellow.
mechanics level of computation. The 5-fluorouracil molecules slip between the layers and the clay swells.
Describing the correct behavior of the rigid guest molecule is more difficult. Using 58 atoms, rather than 300, the 5-fluorouracil stands vertically between the clay layers. At the Hartree-Fock level of computation, 318 basis functions yield near convergence.
Cite this paper
John H.Summerfield, (2015) Simulation of 5-Fluorouracil Intercalated into Montmorillonite Using Spartan ’14: Molecular Mechanics, PM3, and Hartree-Fock. Open Journal of Physical Chemistry,05,49-55. doi: 10.4236/ojpc.2015.53006
References
- 1. Pyra, C. (2015) Colon Cancer. Colon Cancer Alliance, Washington DC, 3.
- 2. Lin, F.H., Lee, Y.H., Jian, C.H., Wong, J., Shieh, M. and Wang, C. (2002) A Study of Purified Montmorillonite Intercalated with 5-Fluorouracil as Drug Carrier. Biomaterials, 23, 1981-1987.
http://dx.doi.org/10.1016/S0142-9612(01)00325-8 - 3. Dixon, J.B. and Weed, S.B. (1989) Minerals in Soil Environments. 2nd Edition, Soil Science Society of America, Madison, 1.
- 4. Dixon, J.B. and Weed, S.B. (1989) Minerals in Soil Environments. 2nd Edition, Soil Science Society of America, Madison, 6-16.
- 5. Dixon, J.B. and Weed, S.B. (1989) Minerals in Soil Environments. 2nd Edition, Soil Science Society of America, Madison, 18-19.
- 6. Dixon, J.B. and Weed, S.B. (1989) Minerals in Soil Environments. 2nd Edition, Soil Science Society of America, Madison, 706.
- 7. Kevadiya, B.D., Patel, H.A., Joshi, G.V., Abdi, S.H.R. and Bajaj, H.C. (2010) Montmorillonite-Alginate Composites as a Drug Delivery System: Intercalation and in Vitro Release of Diclofenac Sodium Indian Journal of Pharmaceutical Sciences, 72, 732-737.
- 8. Ferrell Jr., R.E. (2008) Medicinal Clay and Spiritual Healing. Clays and Clay Minerals, 56, 751-760.
http://dx.doi.org/10.1346/CCMN.2008.0560613 - 9. Helsen, J. (1982) Clay Minerals as Solid Acids and Their Catalytic Properties. Journal of Chemical Education, 59, 1063-1065.
http://dx.doi.org/10.1021/ed059p1063 - 10. Boyd, D.B. and Lipkowitz, K.B. (1982) Molecular Mechanics: The Method and Underlying Philosophy. Journal of Chemical Education, 59, 269-274.
http://dx.doi.org/10.1021/ed059p269 - 11. Cox, P.J. (1982) Molecular Mechanics: Illustrations of Its Application. Journal of Chemical Education, 59, 275-277.
http://dx.doi.org/10.1021/ed059p275 - 12. Halgren, T.A. (1996) Merck Molecular Force Field I. Journal of Computational Chemistry, 17, 490-519.
http://dx.doi.org/10.1002/(SICI)1096-987X(199604)17:5/6<490::AID-JCC1>3.0.CO;2-P - 13. Halgren, T.A. (1996) Merck Molecular Force Field II. Journal of Computational Chemistry, 17, 520-552.
http://dx.doi.org/10.1002/(SICI)1096-987X(199604)17:5/6<520::AID-JCC2>3.0.CO;2-W - 14. Hehre, W.J. and Ohlinger, W.A. (2014) Spartan ’14. Wavefunction, Inc., Irvine.
- 15. Janeba, D., Capková, P. and Schenk, H. (1998) Molecular Simulations of Zn-Montmorillonite. Clay Minerals, 33, 197-204.
- 16. Skipper, N.T., Sposito, G. and Chang, F.C. (1998) Monte Carlo Simulation of Interlayer Molecular Structure in Swelling Clay Minerals. 2. Monolayer Hydrates. Clays and Clay Minerals, 43, 294-303.
http://dx.doi.org/10.1346/CCMN.1995.0430304 - 17. Sutton, R. and Sposito, G. (2002) Animated Molecular Dynamics Simulations of Hydrated Cesium-Smectite Interlayers. Geochemical Transactions, 3, 73-80.
http://dx.doi.org/10.1186/1467-4866-3-73 - 18. Lin, F., Chen, C., Cheg, W. and Kuo T. (2006) Modified Montmorillonite as Vector for Gene Delivery. Biomaterials, 17, 3333-3338.
http://dx.doi.org/10.1016/j.biomaterials.2005.12.029 - 19. Kameyama, H., Narumi, F., Hattori, T. and Kameyama, H. (2006) Oxidation of Cyclohexene with Molecular Oxygen Catalyzed by Calcium Porphyrin Complexes Immobilized on Montmorillonite. Journal of Molecular Catalysis A: Chemical, 258, 172-177.
http://dx.doi.org/10.1016/j.molcata.2006.05.022 - 20. Slater, J.C. (1930) Atomic Shielding Constants. Physical Review, 36, 57-67.
http://dx.doi.org/10.1103/PhysRev.36.57 - 21. Levine, I.N. (1991) Quantum Chemistry. Prentice Hall, Englewood Cliffs, 461-466.
- 22. Froese Fischer, C. (1987) General Hartree-Fock Program. Computer Physics Communication, 43, 355-365.
http://dx.doi.org/10.1016/0010-4655(87)90053-1 - 23. Strout, D. and Scuseria, G.A (1995) Quantitative Study of the Hartree-Fock Method. Journal of Chemical Physics, 102, 8448-8452.
http://dx.doi.org/10.1063/1.468836









