Open Journal of Endocrine and Metabolic Diseases
Vol.2 No.4(2012), Article ID:24454,5 pages DOI:10.4236/ojemd.2012.24008
Surface Tension and Foam Stability Prediction of Polydimethylsiloxane-Polyol Systems
Departamento de Fisicoquímica, Facultad de Química, Universidad Nacional Autónoma de México, México City, México
Email: jgraciaf@unam.mx
Received September 22, 2012; revised October 15, 2012; accepted November 5, 2012
Keywords: Gibbs Elasticity Modulus; Foamability; Langmuir Isotherm; Gibbs Adsorption Equation
ABSTRACT
The Gibbs elasticity modulus represents an important tool to predict the foamability for transient and permanent foams like polyurethane flexible systems. Elasticity is related to foamability and so is used as a synonymous for the purpose of this paper. In this article we propose a method and a thermodynamic model to analyze the espumability of silicone surfactants in polyol binary mixtures using surface tension data. The present work describes foamability through the Gibbs elasticity modulus expressed in terms of first and second derivatives of surface pressure vs bulk composition. Furthermore, the Gibbs adsorption equation and the corresponding novel surface equation of state based on a modification of the Langmuir isotherm resulted in an elasticity equation with analytical solution. It is shown that according to foam model systems of surfactant solution in polyol used at commercial processes, optimum concentration level of surfactant obtained at this article by Gibbs adsorption equation and maximus on elasticity modulus finally match.
1. Introduction
Polyurethane foams are made by mixing an isocyanate and a polyol component [1]. Normally the polyol stream contains additives to achieve the end properties, among these additives are blowing agents, catalysts and surfactants. Silicone surfactant plays an important role in flexible polyurethane foam through decrement of the surface tension. Copolymers of a polydimethylsiloxane are well known and used as surfactants in polyurethane industry. Foam behaviour or foamability is a complex phenomena related with the composition and chemical structure of the amphiphile and depends on many factors such as type of the foam films, surface forces, disjoining pressure, temperature, kinetics of thinning and film rupture, surface and bulk rheology [2,3]. The mechanical properties of the cured polyurethane foam as air permeability and cell size are affected significantly by the structure of the silicone surfactant used in the formulation. Surfactants based Polydimethylsiloxane (PDMS) help with nucleation and in stabilizing foaming mixtures. G. Besmans, L. Colman and R. Vandensande used the maximum bubble pressure method to measure dynamic behavior of these silicone surfactants (PDMS) in the viscous polyol medium, a method which allowed fast screening of novel surfactants [4], that has been proved for measuring the dynamic response of surfactants in aqueous media. According to G. Besmans, L. Colman and R. Vandensande, dynamic surface tension response was measured in methyl capped polyethylene glycol PEG (MW 500 from ICI) using a surfactant loading of 0.1% by weight. Surfactants were obtained from Goldschmidt AG, Osi, and Air Products.
Commercially polydimethylsiloxane based surfactants are of a polymeric nature with a natural spread of molecular weight. The exact structure is part of the proprietary knowledge of the surfactant suppliers (Figure 1), but can be described with the formula where D is dimethylsiloxane and D is methylsiloxane with polyoxyalkylene, susbstitute R is composed of polyethylene oxide and polypropylene oxide [4].
2. Materials and Methods
Analytical grade nonyl phenol ethoxylates were purchased from Sigma and used with no further purification.
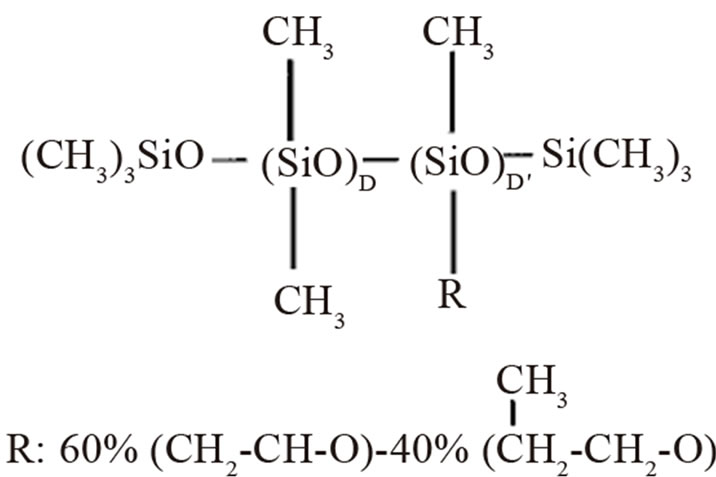
Figure 1. The structure of a typical surfactant used in polyurethane foam systems.
Silicone Tegostab BF-2370 provided by Goldschmidt AG (Figure 2), was used as surfactant with a molecular mass of 8800 g/mol [5]. The polyol polypropylene glycol was supplied by Sigma Aldrich, molecular mass is 2700 g/mol. Pluronic L61 (BASF) is a block copolymer, the average molecular mass is 2000 g/mol, consisting of 10% ethylene oxide and 90% propylene oxide.
Surfactant-polyol mixtures were prepared at controlled temperature of 30˚C. The samples were placed in a thermostated vessel during the surface tension measurements and the temperature was regulated (within ± 0.1˚C).
Surface tension methods A dynamic method for surface tension was chosen, the maximum bubble pressure method displayes surface tension based on instantaneous bubble formation [6-8]. This is a dynamic method selected for surface tension measurements due to polyurethane foam formulation taking seconds during its production.
Surface tension vs composition was measured using QC3000 SensaDyne Surface Tensiometer (within ±0.1 dyne/cm) fitted with a bath (Haake K20/DC30) allowing to control the temperature (within ±0.1˚C). An inert process gas (nitrogen or dry air) is bubbled slowly through two probes of different radio that are immersed in a test fluid. The bubbling of the nitrogen through the probes produces a differential pressure signal (ΔP) which is directly related to the fluid surface tension (σ).
The Young-Laplace equation rules the relation among curvature, surface energy and pressure difference between two phases; it has been used to describe spherical and non spherical shapes either in the absence or under the influenece of an external field. The general expression for the mechanical equilibrium between phases separated by spherical surface is
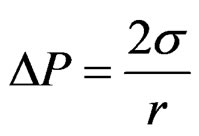 (1)
(1)
where r is the sphere radius and DP is the difference in the pressure between phases. The difference in the pressure P2 at the large probe from the pressure P1 at the small probe results in a differential pressure equation keeping the two probes at the approximate same immersion depth cancelling the effects of liquid level (Figure 3), and the additional variation in the hydrostatic pressure caused by the gravitational field effect.
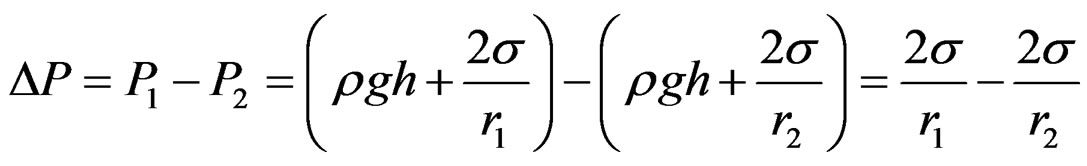 (2)
(2)
Foam formation test Foam was produced using a glass column of 1000 ml fitted at the bottom with a porous glass disk. Samples of the polydimethylsiloxane dispersions were carefully pured into the column and foam was produced at a constant temperature of 30˚C by passing gas trough the porous glass (pore diameter 0.2 μm) at a controlled flux between 20 and 60 ml/min during ten minutes (Figure 4). Surfactant concentration ranged between 0.05 and 1.2 wt%. Results were expressed as foamability or the volume produced by a weight fraction of surfactant in polyol.
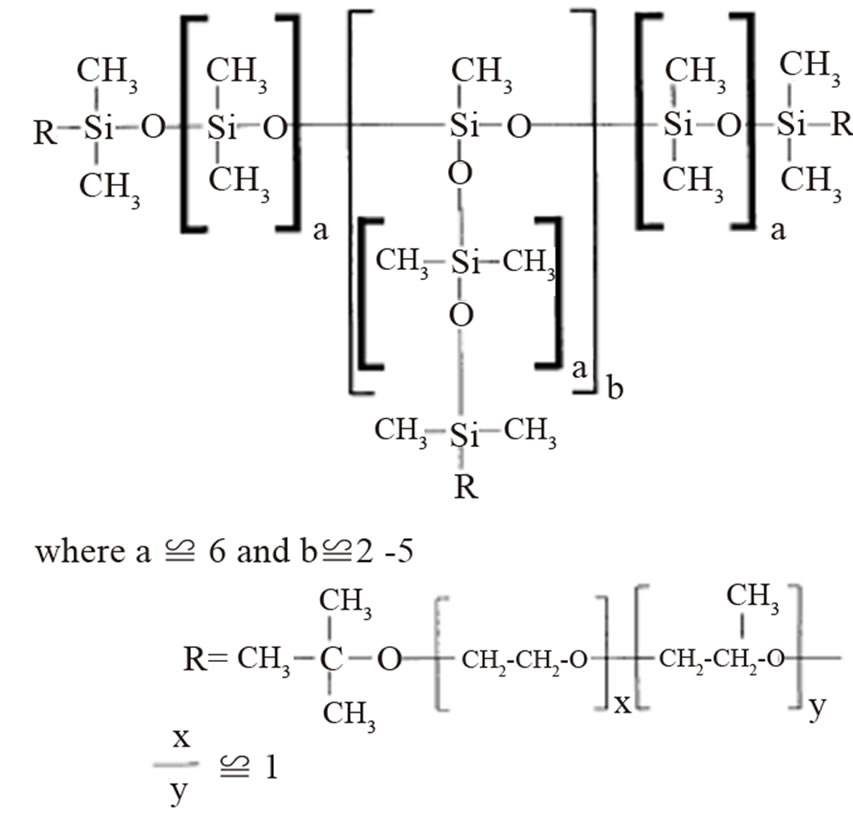
Figure 2. Structure of tegostab BF 2370.
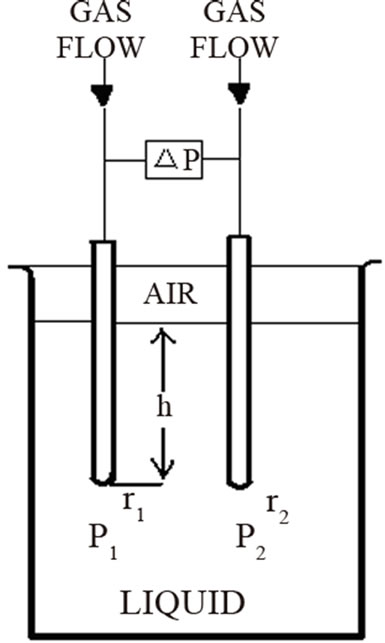
Figure 3. Differential pressure schematic.
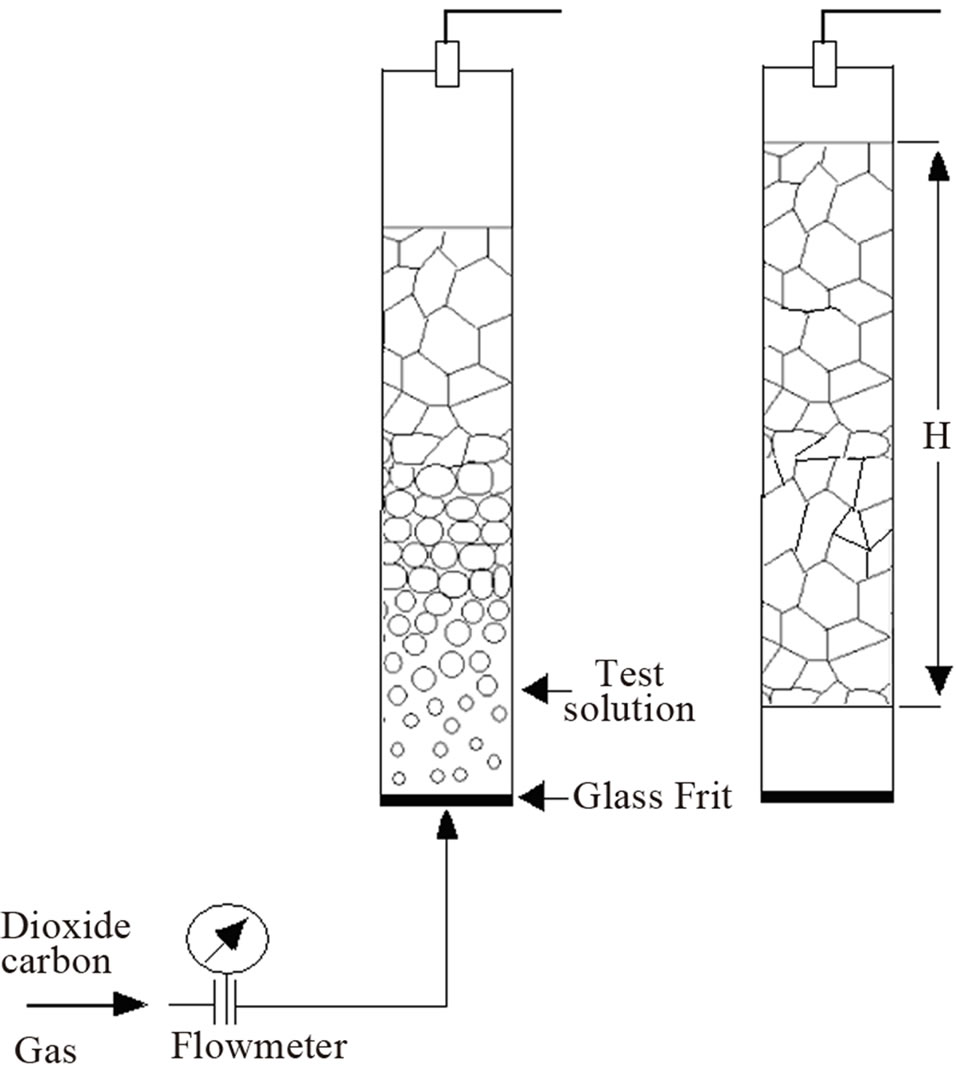
Figure 4. Schematics of the foam column test.
3. Results and discussion
Although surface properties for both kinds of polyols were similar (Figure 5), foaming behaviour presented differences (Figure 6). The foaming behaviour increased with concentration, with a maximum around the critical concentration and then decreased; an expected behaviour for transient foams.
Some works have been published describing methods to calculate equilibrium constants of molecular complexes in aqueous solution or to predict activity coefficients at infinite dilution from surface tension data [9, 10]. In this line it has been recently developed a model [11], able to describe the dependence of the surface tension on the concentration for a wide variety of solutions with different behavior (Figures 7 and 8), the model has been named Langmuir modified [12], that can be expressed as
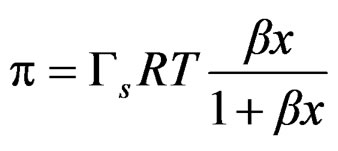 (3)
(3)
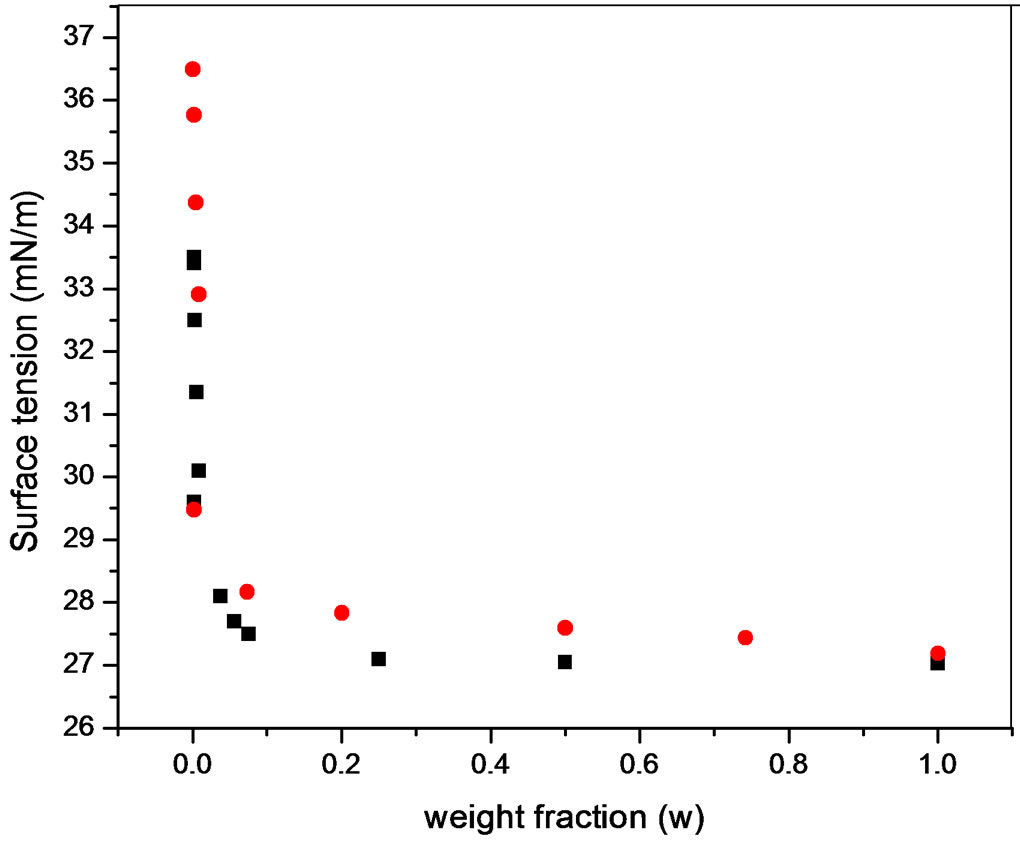
Figure 5. Surface tension at 30˚C of PDMS at (·) Polypropylene glycol and (¡) Pluronic L61.
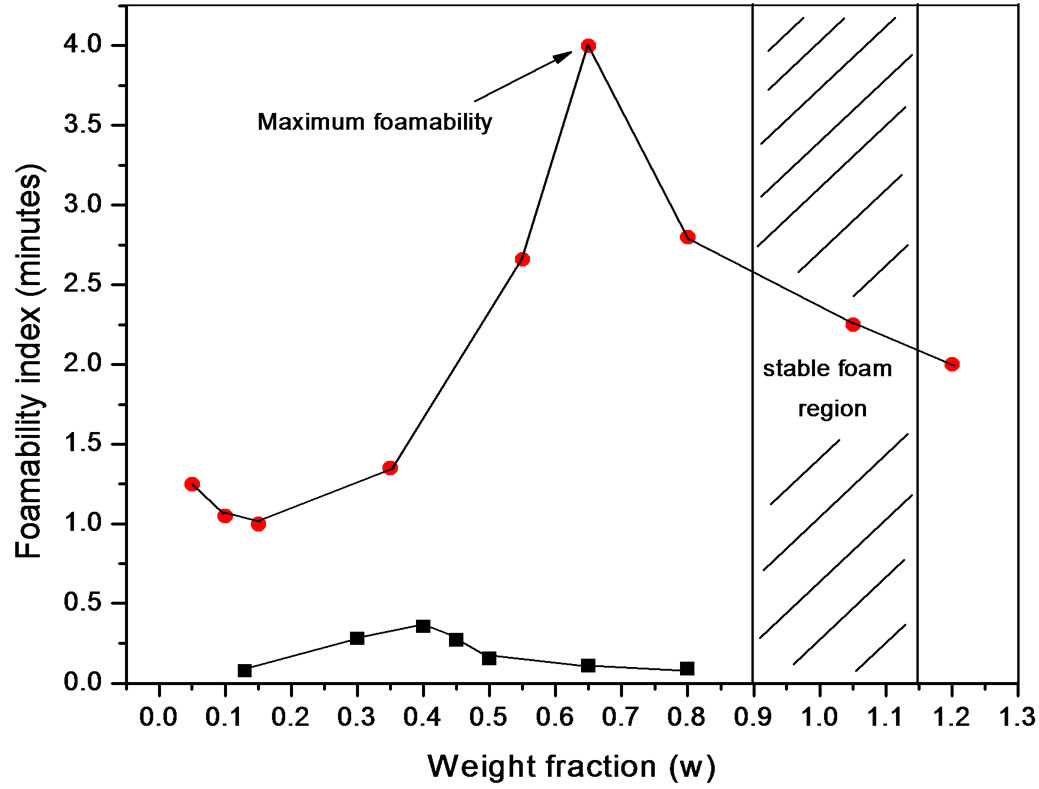
Figure 6. Foamability at 30˚C of PDMS at (·) Polypropylene glycol and (¡) Pluronic L61.
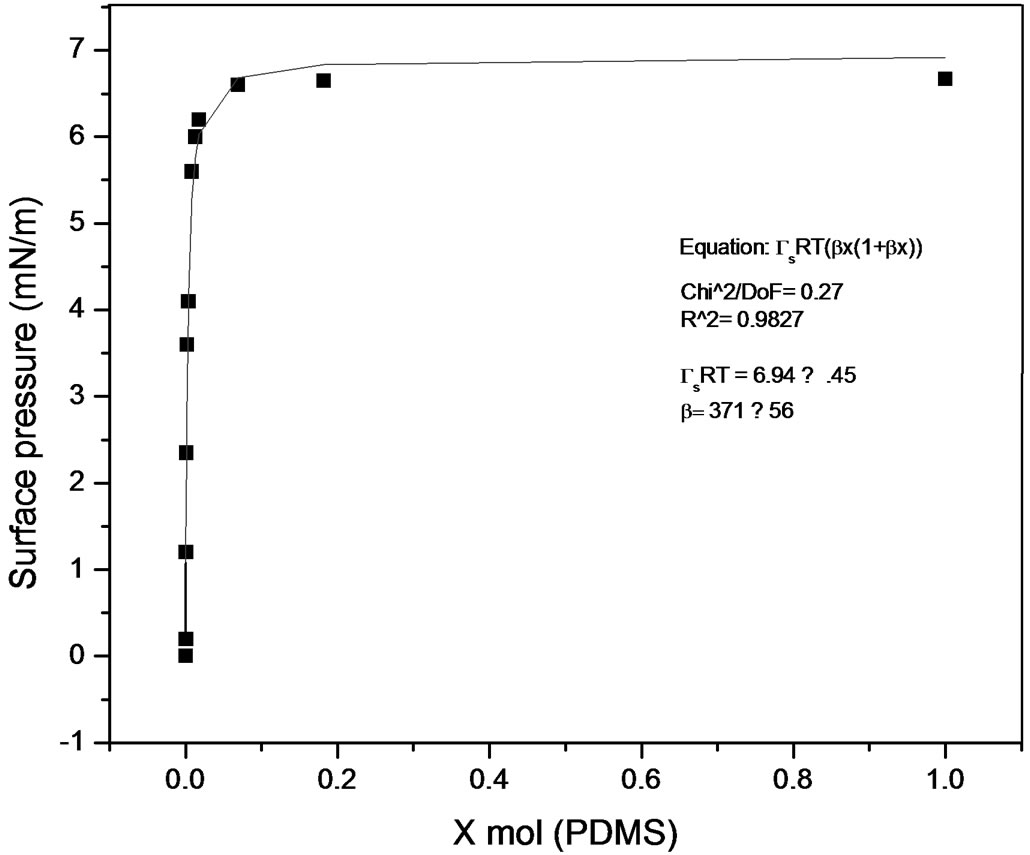
Figure 7. Langmuir modified. Pluronic L61-PDMS system.
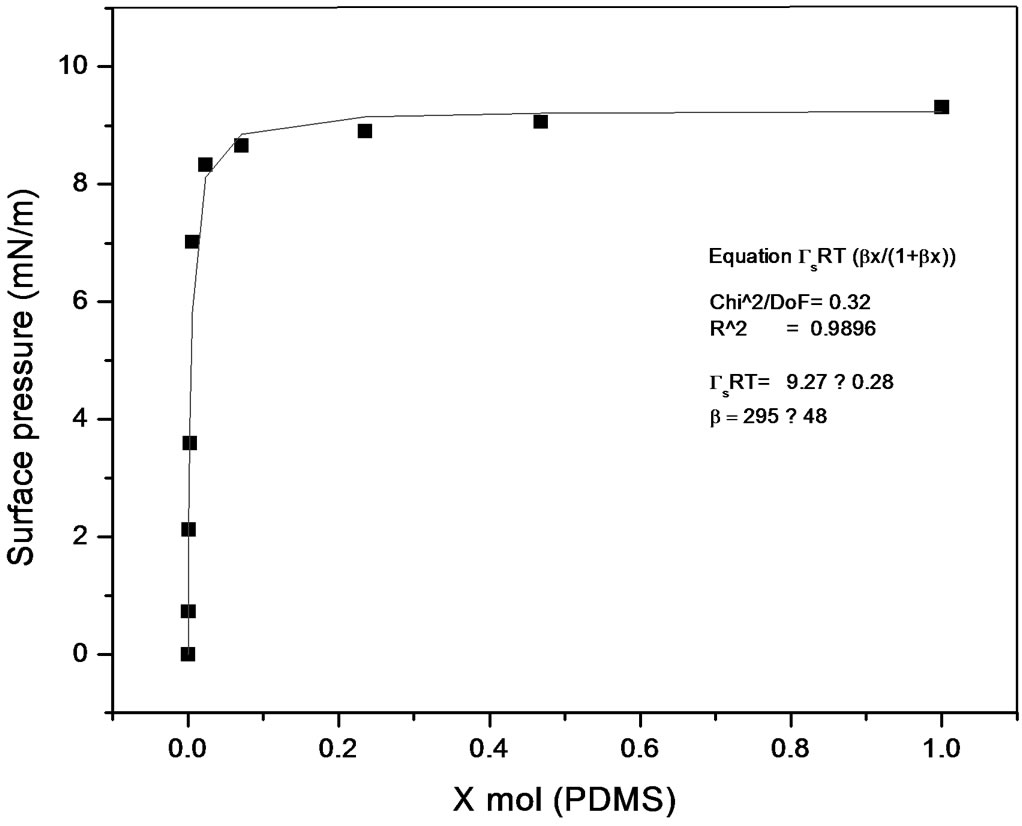
Figure 8. Langmuir modified. Polypropylene glycol-PDMS system.
where p is surface pressure, Γ is the excess surface concentration and is equall to the reciprocal area, Gs is the maximum surface concentration, R is the universal gas constant, T is the absolute temperature and β is a measure of the lyophobicity, so, based on the Langmuir isotherm, where θ is the surface coverage,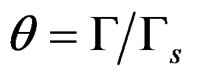 ;
;
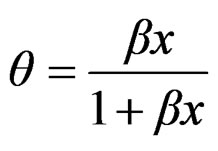 (4)
(4)
The Gibbs adsorption isotherm allows us to transform an isotherm to a surface equation of state [13]. The Langmuir isotherm in fluid-fluid interfaces, coupled with the Gibbs equation, leads to;
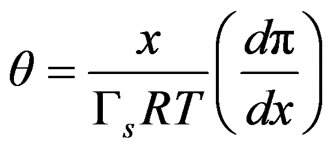 (5)
(5)
The combination of Equations (4) and (5) and integral form leads to the corresponding surface equation of state SEOS
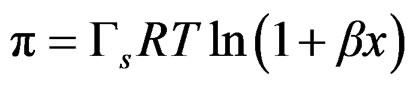 (6)
(6)
from the Lagmuir-Frumkin equation;
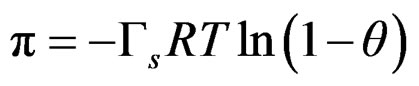 (7)
(7)
Equation (7) does not include atractive effects, so is proposed a general function f(θ);
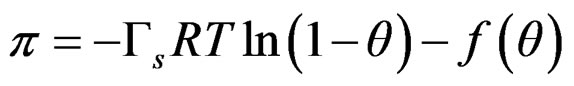 (8)
(8)
That can be expressed as series expansion;
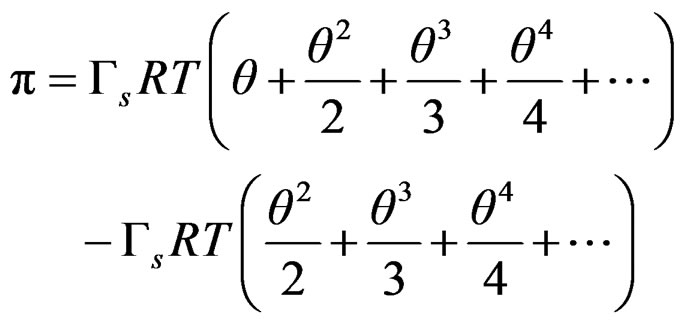 (9)
(9)
Obtaining the final Equation (3) to which the experimental data are fitted;
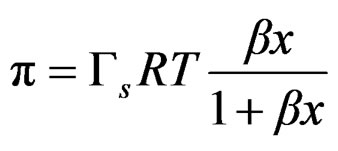
Polidimethylsiloxanes form transient foams in polyols, meaning that the foam is present as long as the gas flux is present and depended on concentration. Pluronic L61 showed lower foamability with bubbles breaking up as soon as the gas flux was interrupted. On the other hand Polypropylene glycol showed better foamability with a maximum that coincides with the critical concentration just as predicted for transient foams.
Gibbs elasticity modulus is closely related to foamability and is expressed as;
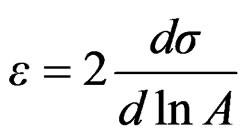 (10)
(10)
Г is the surface concentration and is equal to the reciprocal of the molecular area;
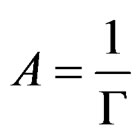 (11)
(11)
leads to the equation;
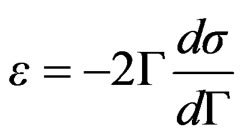 (12)
(12)
Surface tension expressed as surface pressure;
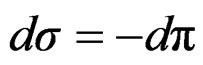 (13)
(13)
Expressions (12) and (13) can be substituted in Equation (10) providing;
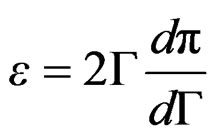 (14)
(14)
Surface pressure can be used instead of surface tension and the associated area changed for specific area, thus
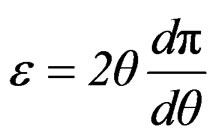 (15)
(15)
That can be expressed as;
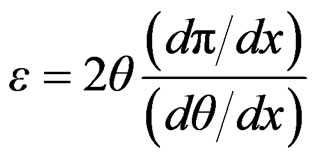 (16)
(16)
From Gibbs adsorption equation;
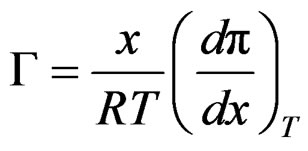 (17)
(17)
Surface coverage can be used instead of surface tension, so
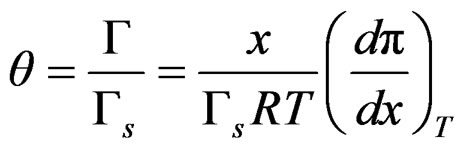 (18)
(18)
The first derivative with respect to mol fraction is;
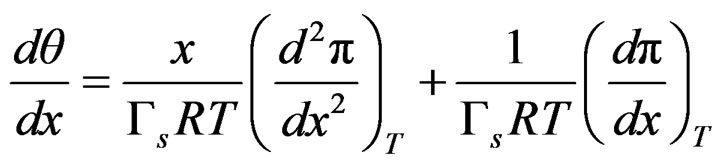 (19)
(19)
By substituing relationships (18) and (19) into Equation (16) to express Gibbs elasticity modulus as;
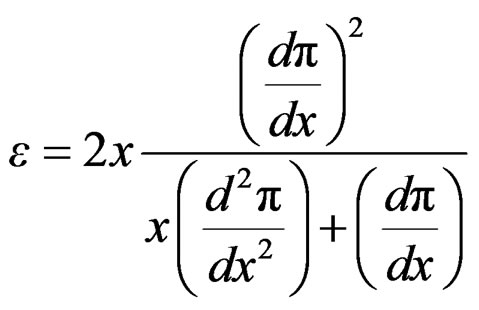 (20)
(20)
The combination of Equation (3) and (20) leads to
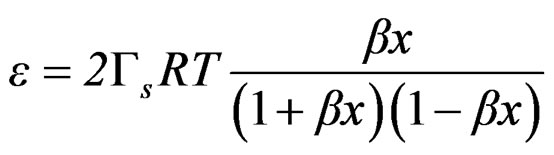 (21)
(21)
Equation (21) can be expressed as follows;
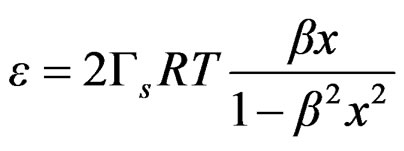 (22)
(22)
The bulk concentration x is related to the surface concentration θ and the foam goes to maximum (Figure 9 and Figure 10), it happens when x= 1/b ; beyond the critical concentration, the surface coverage is completed and the surface pressure remains constant thus Gibbs elasticity modulus goes to zero and the foam decays [14-17]. The concentration level where the maximum foam volume was obtained agrees with the concentration level on polyurethane foam formulations.
4. Conclusion
It has been shown that it is possible to characterize the surface tension of polydimethylsiloxane based surfactants in viscous model systems of a polyurethane foam forming medium. Even though both polyols don’t share same characteristics, the surface tension equilibrium was very similar when PDMS is involved as surfactant. However Pluronic L61 presented poor foaming behaviour explained by the rectification process ocurring along the foam column. PDMS showed transient foam behaviour with maximum foamability around concentration level
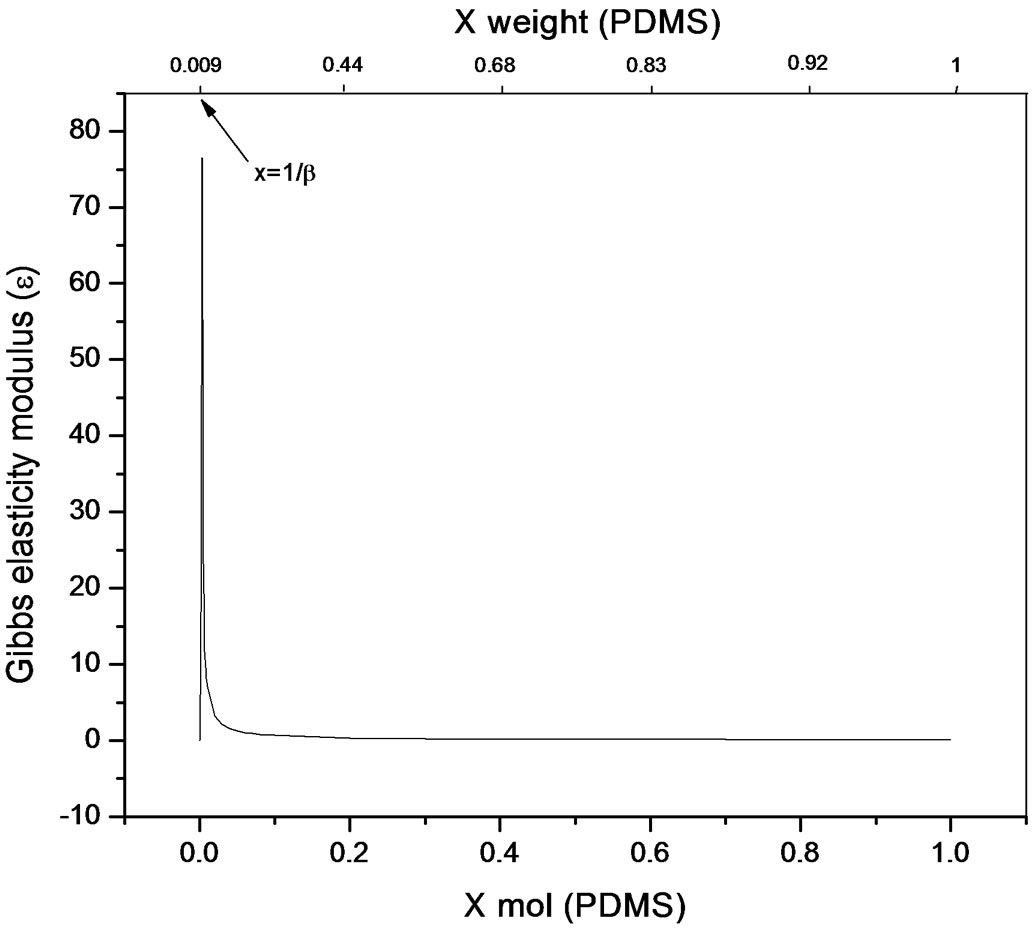
Figure 9. Gibbs elasticity modulus. Polypropylene glycolPDMS system (Equation (22)).
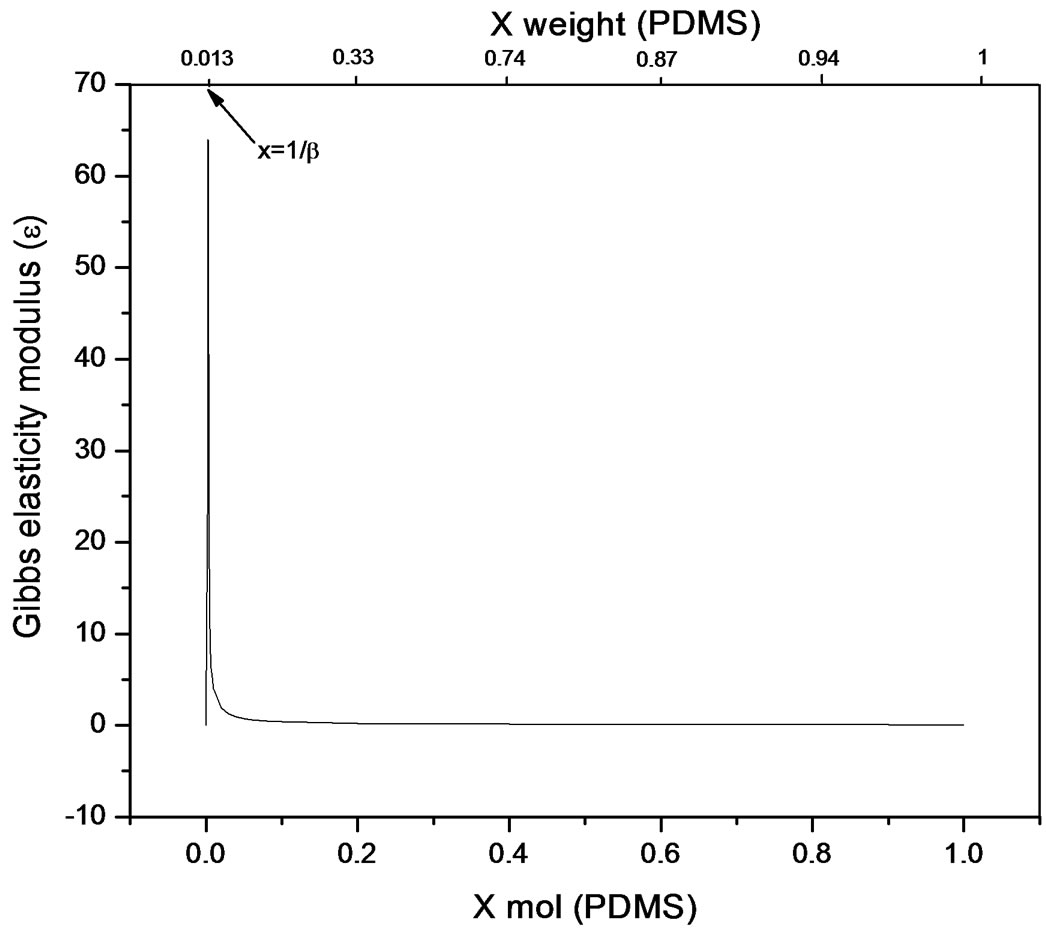
Figure 10. Gibbs elasticity modulus. Pluronic L61-PDMS system (Equation (22)).
used in polyurethane foam formulations. Polypropylene glycol presented better foaming properties compared to Pluronic L61 which had poor foaming behaviour explained by the rectification process ocurring along the foam causing Pluronic a lower capability to re-establish the surface concentration limiting the adsorption to the newly created surfaces. Even though foam is a dispersed system and hence out of equilibrium, the hypothesis of local chemical equilibrium between lamellar solution and foam’s surface shows a proximity towards equilibrium conditions and allows for the thermodynamic description of elasticity; which for the purpose of this work was referred to foamability. The equation presented allows a direct relation to the Gibbs adsorption equation and is applicable for transient foams to predict concentration stability zone for polyurethane flexible systems that involve polidymethylsiloxane-poliol mixtures, where foamability decreases beyond a critical concentration. Foamability, or the foam volume produced by an amphiphile in a viscous medium like a poliol at a given concentration, is satisfactorily described by means of the Gibbs elasticity modulus (ε) presented in terms of the first and second derivatives of surface pressure and the bulk concentration.
5. Acknowledgements
This work was supported by Dirección General de Administración del Personal Académico (DGAPA) under the project PAPIIT-IT118711.
REFERENCES
- R. Herrington and K. Hock, “Flexible Polyurethane Foams,” 2nd Edition, Dow Chemical Co., Midland, 1997.
- A. W. Adamson, “Physical Chemistry at Interfaces,” 6th Edition, John Wiley & Sons Inc., New York, 1997.
- M. J. Rosen, “Surfactants and Interfacial Phenomena,” 2nd Edition, Wiley Interscience, New York, 1989.
- G. Biesmans, L. Colman and R. Vandensande, “The Use of Principal Component. Analysis to Classify PDMS Surfactants Used to Make Rigid Polyurethane Foams Based on Their Dynamic Surface Tension Characteristics,” Journal of Colloid and Interface Science, Vol. 199, No. 2, 1998, pp. 140-150. doi:10.1006/jcis.1997.5337
- X. D. Zhang, C. W. Macosko, H. T. Davis, A. D. Nikolov and D. T. Wasan, “Role of Silicone in Flexible Polyurethane Foam,” Journal of Colloid and Interface Science, Vol. 215, No. 2, 1999, pp. 270-279. doi:10.1006/jcis.1999.6233
- B. D. Kaushiva, S. R. McCartney, G. R. Rossmy and G. L. Wilkes, “Surfactant Level Influences on Structure and Properties of Flexible Slabstock Polyurethane Foams,” Polymer, Vol. 41, No. 1, 2000, pp. 285-310. doi:10.1016/S0032-3861(99)00135-4
- J. Eastoe, J. Dalton, G. Rogueda, E. Crooks, A. Pitt and E. Simister, “Dynamic Surface Tension of Nonionic Surfactant Solutions,” Journal of Colloid and Interface Science, Vol. 188, No. 2, 1997, pp. 423-430. doi:10.1006/jcis.1997.4778
- P. Joos, J. P. Fang and G. Serrien, “Comments on Some Dynamic Tension Measurements by the Dynamic Bubble Pressure Method,” Journal of Colloid and Interface Science, Vol. 151, No. 1, 1992, pp. 144-149. doi:10.1016/0021-9797(92)90245-H
- J. Eastoe and J. S. Dalton, “Dynamic Surface Tension and Adsorption Mechanisms of Surfactants at the Air-Water Interface,” Advances in Colloid and Interface Science, Vol. 85, No. 2-3, 2000, pp. 103-144. doi:10.1016/S0001-8686(99)00017-2
- J. Viades-Trejo and J. Gracia, “A New Surface Equation of State Hydrophobic-Hydrophilic Contributions to the Activity Coefficient,” Fluid Phase Equilibria, Vol. 264, No. 1-2, 2008, pp. 12-17.
- J. Viades-Trejo, A. Amigo and J. Gracia, “Activity Coefficients at Infinite Dilution for Surfactants,” Fluid Phase Equilibria, Vol. 250, No. 1-2, 2006, pp. 158-164. doi:10.1016/j.fluid.2006.10.015
- A. Piñeiro, P. Brocos, J. Gracia and A. Amigo, “Application of the Extended Langmuir Model to Surface Tension Data of Binary Liquid Mixtures,” Fluid Phase Equilibria, Vol. 237, No. 1-2, 2005, pp. 140-151. doi:10.1016/j.fluid.2005.08.020
- E. O. Magaña, “Identificación de Fuerzas Intermoleculares en la Interfase Mediante Ecuaciones de Langmuir,” Tesis de Licenciatura, U.N.A.M., 2008.
- J. Gracia, “Langmuir-BET Surface Equation of State in Fluid-Fluid Interfaces,” Langmuir, Vol. 15, No. 9, 1999, pp. 3279-3282. doi:10.1021/la981244o
- J. G. Fadrique, “Cinética de Adsorción Superficial,” Tesis de Maestría, U.N.A.M., 1979.
- G. Bleys and P. Joos, “Adsorption Kinetics of Bolaform Surfactants at the Air/Water Interface,” Journal of Physical Chemistry, Vol. 89, No. 6, 1985, pp. 1027-1032. doi:10.1021/j100252a028
- F. Elizalde, J. Gracia and M. Costas, “Effect of Aggregates in Bulk and Surface Properties. Surface Tension, Foam Stability and Heat Capacities for 2 Butoxyethanol + Water,” Journal of Physical Chemistry, Vol. 92, No. 12, 1988, pp. 3565-3568. doi:10.1021/j100323a048

