Open Journal of Physical Chemistry
Vol. 2 No. 1 (2012) , Article ID: 17521 , 6 pages DOI:10.4236/ojpc.2012.21001
Study of Thermal Conductivity of Porous Silicon Using the Micro-Raman Method
Research Unit Materials and Renewable Energy (RUMRE), University of Abou Bekr Belkaid of Tlemcen, Tlemcen, Algeria
Email: aouldabbes@yahoo.fr
Received April 29, 2011; revised August 3, 2011; accepted November 8, 2011
Keywords: Mono-Crystal Silicon; Porous Silicon; Thermal Conductivity; Micro-Raman Spectroscopy
ABSTRACT
In this work, we are interesting in the measurement of thermal conductivity (on the surface and in-depth) of Porous silicon by the micro-Raman spectroscopy. This direct method (micro-Raman spectroscopy) enabled us to develop a systematic means of investigation of the morphology and the thermal conductivity of Porous silicon oxidized or no. The thermal conductivity is studied according to the parameters of anodization and fraction of silicon oxidized. Thermal transport in the porous silicon layers is limited by its porous nature and the blocking of transport in the silicon skeleton what supports its use in the thermal sensors.
1. Introduction
Porous silicon (PS) is obtained by electrochemical attack of single crystalline silicon [1]. PS is a tuneable material in respect of its pore size distributions depending on its formation conditions. From the macro-porous silicon (with thickness bigger than 0.1 µm or 0.1 nm) to the meso-porous silicon (about 2 to 100 nm of thickness) to the nano-porous silicon (thickness smaller than 10 nm), the range of its applications varies. This material is used in photonics and optoelectronics [2], quantum electronics [3], silicon-on insulator technology [4] and very recently in sensors [5]. Since the last decade, PS has also been investigated in the area of photovoltaic [6] as an antireflection coating and as a sacrificial layer for the layer transfer process (LTP) [7,8].
This material presents a thermal conductivity near to thermal conductivity of silicon dioxide [9]. This material is an excellent candidate to ensure the thermal insulation for the micro sensors on silicon because it ensures the mechanical stability of the microstructure [10]. For this reason, PS layers have been effectively used as material for local thermal isolation on bulk silicon [11,12] and as material for the fabrication of micro-hotplates for lowpower thermal sensors [13,14]. Nevertheless, before implementing the PS sensor, it is necessary to understand the thermal transport in such nanostructure and the experimental study of its thermal conductivity, according to its characteristic parameters.
In this work, we are interesting in anodization of silicon to release the principal factors, acting on the morphology in-depth of the layer. We expose a direct method of measurement of the thermal conductivity for PS layers. This parameter is founded on their micro-Raman response to a laser excitation producing a thermal gradient in material. This latter is evaluated by the micro-Raman spectroscopy. The analysis of surface and indepth distribution of the crystallites composing the material is presented.
2. Experimental Procedure
The PS samples were prepared by electrochemical anodic etching of p-type, (100)-oriented, 0.01 - 0.025 Ω·cm–1 silicon wafers, in a solution of HF (48%):C2HÖH of 1:1. Current densities range were 5 and 75 mA/cm2 during 10 min. The current density and the time attack selected permit to obtain different layers with different porosities and different thicknesses. After the electrochemical treatment, samples were rinsed in deionized water and were dried under nitrogen flow.
Samples prepared in this study are described in Table 1.
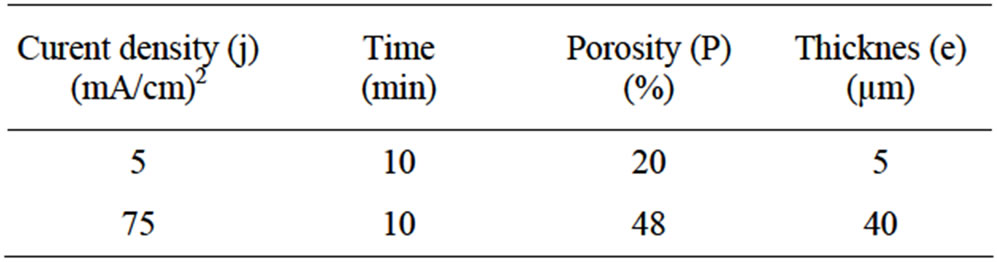
Table 1. Anodization parameters of the samples prepared with two current densities.
Thereafter, a thermal oxidation at low temperature (300˚C) under dry atmosphere of O2 is applied on these samples in order to stabilize the whole structure mechanically and to allow carrying out following treatments [15,16]. We called t his stage “pre-oxidation”.
Meso-porous layers of 175 µm thickness were obtained by complex methods then were oxidized under dry atmosphere at different temperature (between 300˚C and 700˚C).
The thermal characterization was carried out by micro-Raman spectroscopy in order to determine the size of crystallites of PS as well as thermal conductivity according to the parameters of anodization. Figure 1 shows a schematic diagram of the micro-Raman method [17].
The laser used for our measurements is an Argon laser with a wavelength of 514 nm. The spectra Raman Stokes are collected in parallel polarization, in retro-diffusion mode using a microscope Olympus BH2, coupled to a monochromator Dilor XY and of a CCD detector (Charge Coupled Detector).
3. Theory
3.1. Thermal Conductivity of Prepared Nano-Porous Silicon
The description of thermal transport of a nanostructured porous material necessarily passes by considerations of a morphological nature The introduction of a percolation factor g0 proposed by Gesele et al. [10], allows to account for structural microphone-topology and is interpreted like the solid fraction of inter-connected phase contributing to thermal transport.
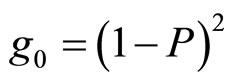 (1)
(1)
 (2)
(2)
Kcr conductivity describes elementary contribution to thermal transport of each quasi-spherical crystallite forming the column-like pseudo network.

Figure 1. Schematic diagram of the micro-raman method.
Because of their nanometric dimension rcr = 8 - 12 nm lower than 7 times the mean free path phonons in single-crystal silicon at ambient temperature ΛSi = 43 nm [18,19], the transport of heat in a crystallite is not described any more by the traditional model of Fourier.
In this case, the phonons are diffused in crystallites and neither variation in temperature, nor thermal conductivity cannot be defined there. Only, the diffusion of phonons to the interfaces makes it possible to locally restore thermodynamic balance [9]
The transport of phonons intervenes according to a ballistic phenomenon between two interfaces. Their mean free path effective ΛSi is then defined according to their lenght de diffusion in single-crystal silicon ΛSi and of the size of crystallites rcr [16]. Effective thermal conductivity in each crystallite is written [20].
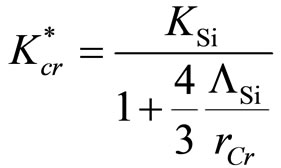 (3)
(3)
Hence,  can be determined as:
can be determined as:
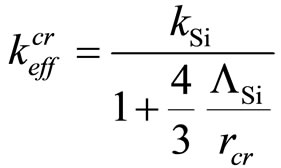 (4)
(4)
Replacing the value of  from Equations (2) and (4) to Equation (1), we obtain the final form of thermal conductivity of nano-PS:
from Equations (2) and (4) to Equation (1), we obtain the final form of thermal conductivity of nano-PS:
 (5)
(5)
The variation of thermal conductivity with the porosity of as prepared nano PS layer, for different sizes of non-oxidized Si nanocrystallites is presented in Figure 2, r is crystallite size of PS.
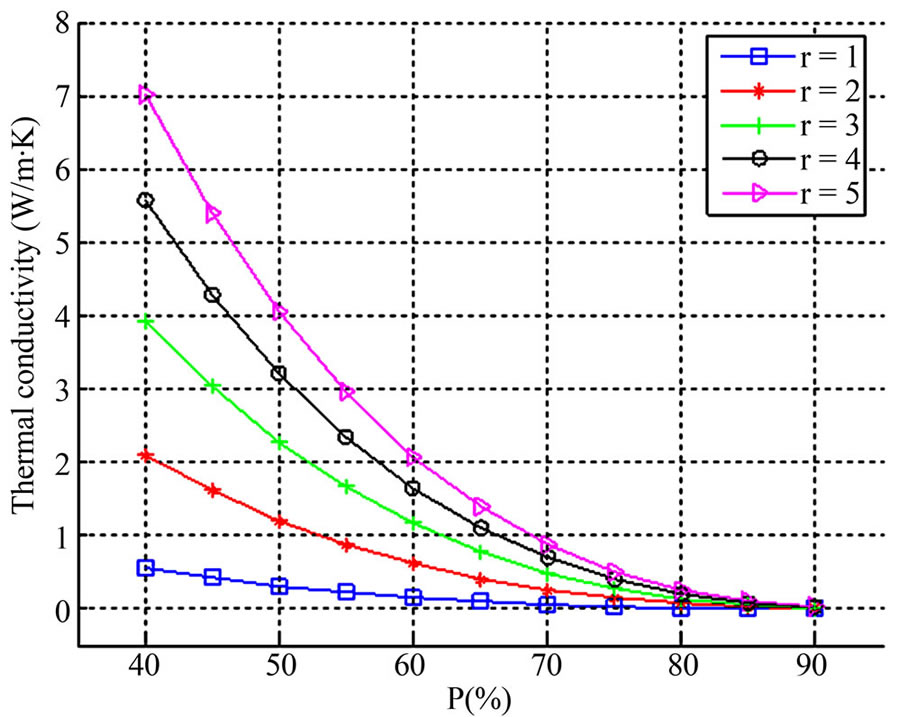
Figure 2. Variation of thermal conductivity with the porosity of as-prepared nano-porous silicon layer.
3.2. Thermal Conductivity of Oxidized Nano-Porous Silicon
After oxidation, each Si crystallite is covered with a SiO2 sheet and its initial size is reduced. In this case, the thermal conductivity of the remaining Si core of the partially oxidized Si/SiO2 crystallite 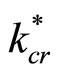 can be expressed as:
can be expressed as:
 (6)
(6)
where  is the oxidized fraction of the origin Si crystallite and it is defined as:
is the oxidized fraction of the origin Si crystallite and it is defined as:
 (7)
(7)
where V0 is the initial volume of Si nano-crystallite, V0* is the total volume of the crystallite after oxidation procedure and VSi* is the volume of Si core of the oxidized crystallite. Coefficient 2.27 [21] considers extension of the crystallite volume after oxidation.
It is easily proved that total thermal conductivity of oxidized nano-PS  can be written as:
can be written as:
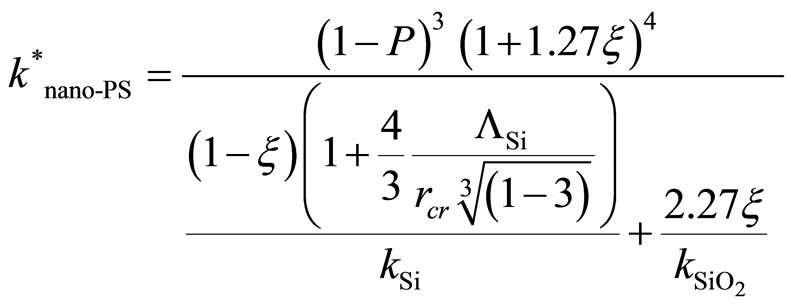 (8)
(8)
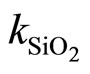 is the thermal conductivity of the dioxide silicon.
is the thermal conductivity of the dioxide silicon.
The variation of thermal conductivity with oxidized fraction of nano-porous silicon layer, for three different sizes of the original non-oxidized Si nanocrystallites is presented in Figure 3.

Figure 3. Dependence of the thermal conductivity of a nano PS layer of its oxidized fraction for three different sizes (r) of silicon nanocrystallites porosity of the layer is 56%.
The function 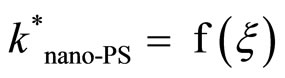 decreases in the range of small
decreases in the range of small 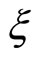 values and has a minimum value (for rcr of 2 - 3 nm). It corresponds to heat transport preferably through the decreased Si cores. Then, k*nano-PS increases along the increase of oxidized fraction, because of the heat transport occurring through the growing oxide sheet, and comes up to the thermal conductivity value of silicon dioxide (1.4 Wm−1·K−1) when the porous silicon layer is completely oxidized and transformed to a SiO2 layer [22,23].
values and has a minimum value (for rcr of 2 - 3 nm). It corresponds to heat transport preferably through the decreased Si cores. Then, k*nano-PS increases along the increase of oxidized fraction, because of the heat transport occurring through the growing oxide sheet, and comes up to the thermal conductivity value of silicon dioxide (1.4 Wm−1·K−1) when the porous silicon layer is completely oxidized and transformed to a SiO2 layer [22,23].
3.3. Determination of the Crystallites Size
In the determination of crystallites the size, we use Campbell and Fauchet method [24]. It consists in correlating position and/or width with middle height of the Raman response of the semiconductor to crystallites size. In order to control morphology on the surface and in-depth of SiP layers, it is necessary to measure the size of crystallites forming material. Moreover, the thermal properties of the layer depend directly on their value. Raman Stokes intensity, obtained with low laser power, is modeled by the following equation:
 (9)
(9)
with 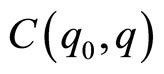 Fourier coefficients resulting from the decomposition of wave function in material in Fourier series, ω(q) the curve of dispersion of phonons and Γ0 the width with middle height of the Raman peak of crystalline material. In the case of mesoporous silicon, we choose
Fourier coefficients resulting from the decomposition of wave function in material in Fourier series, ω(q) the curve of dispersion of phonons and Γ0 the width with middle height of the Raman peak of crystalline material. In the case of mesoporous silicon, we choose 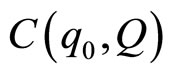 with a function of containment of phonons in quasi-spherical crystallites such as:
with a function of containment of phonons in quasi-spherical crystallites such as:
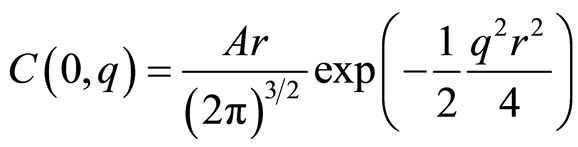 (10)
(10)
with r crystallites size, A constant and Q wave vector.
4. Results and Discussion
The results presented in Table 2 on the size of crystallites are obtained from the measurement of the width middle height of Raman peak function.
The exploitation of Raman spectra can lead to the determination of crystallites size only when the incidental power laser is low for not provokes the heating of the surface (which would modify the position and the shape

Table 2. Crystallites sizes obtained from the raman analyses.
of the spectra) (Figure 4).
By the method of micro characterization Raman, presented in a preceding study [24]. The method of measurement that we developed is founded on two effects complementary to the micro-Raman spectroscopy. The first is the use of the laser beam localised on the surface of material like local source of heating. The rise in the temperature resulting depends mainly on thermal conductivity from the sample. The second effect is the displacement of the peak Raman with the temperature of the sample, which makes it possible to deduce the local rise in the temperature from material.
By using the linear model suggested by Nonnenmacher [25], the thermal conductivity of a material in thin layer can be written in the form:
 (11)
(11)
with P the power of heating, Tj the temperature of surface and Ts the temperature of the substrate, has the diameter of the laser spot, We obtained the following results. The porosity is directly, related to the nano-structure of material. It is the principal parameter acting on thermal conductivity, Figure 5 shows that thermal conductivity decreases when porosity increases. This is explained by the effect of reduction of the effective size of the nano-crystals silicon; when porosity increases, crystallites size decreases as well as surfaces of interconnection between crystallites what more reduces the thermal way by conduction in the silicon skeleton.
The variations of thermal conductivity with the temperature of porous silicon are presented in Figure 6 for three porosities. Each sample has a thickness of 50 µm. Their thermal conductivity is measured after anodization and after oxidation during 1 hour, in dried O2 at 150˚C, 300˚C and at last at 450˚C.

Figure 4. Raman spectra of the sample (J = 5 mA/cm2, t = 10 mn).

Figure 5. Thermal conductivity of meso PS samples oxidized 1h under dry O2.

Figure 6. Thermal conductivity of meso-PS obtained according to oxydation temperature at 150˚C, 300˚C and 450˚C.
Whatever their porosity, the thermal conductivity of the samples follows the same evolution. Conductivity decrease initially until reaching a minimum then increases slightly
5. Conclusions
The micro-Raman spectroscopy enabled us to develop a systematic means of investigation of morphology and thermal conductivity of porous silicon. The thermal conductivity of porous silicon was studied according to the parameters of anodization (initial doping and current density and rate oxidation).
One will retain the principal following tendencies:
• Thermal conductivity strongly decrease when the layer porosity increases.
• Oxidation under dried O2 induced a strong decrease of conductivity to reach a minimum.
The thermal conductivity of porous silicon is quite lower than that of mono-crystal silicon. Thermal transport in the porous silicon layers is limited by its porous nature and the blocking of transport in the silicon skeleton what supports its use in the thermal sensors.
6. Acknowledgements
The authors wish to thank S. Perichon and D. Barbier for Raman manipulations and for their fruitful discussions
REFERENCES
- L. T. Canham, “Silicon Quantum Wire Array Fabrication by Electrochemical and Chemical Dissolution of Wafers,” Applied Physics Letters, Vol. 57, No. 10, 1990, pp. 1046-1049. doi:10.1063/1.103561
- A. G. Cullis, L. Canham and P. D. J. Calcott, “The Structural and Luminescence Properties of Porous Silicon,” Journal of Applied Physics, Vol. 82, No. 3, 1997, pp. 909-962. doi:10.1063/1.366536
- A. J. Read, R. J. Needs, K. J. Nash, L. T. Canham, P. D. J. Calcott and A. Qteish, “First-Principles Calculations of the Electronic Properties of Silicon Quantum Wires,” Physical Review Letters, Vol. 69, No. 8, 1992, p. 1232. doi:10.1103/PhysRevLett.69.1232
- G. Bomchill, A. Halimaoui and R. Herino, “Porous Silicon: The Material and Its Applications to SOI Technologies,” Microelectronic Engineering, Vol. 8, No. 3-4, 1988, pp. 293-310. doi:10.1016/0167-9317(88)90022-6
- A. Foucaran, B. Sorli, M. Garcia, F. Pascal-Delannoy, A. Giani and A. Boyer, “Porous Silicon Layer Coupled with Thermoelectric Cooler: A Humidity Sensor,” Sensors & Actuators, Vol. 79, No. 3, 2000, pp. 189-193. doi:10.1016/S0924-4247(99)00285-X
- R. Bilyalov, L. Stalmans, G. Beaucarne, R. Loo, M. Cayman, J. Poortmans and J. Nijs, “Porous Silicon as an Intermediate Layer for Thin-Film Solar Cell,” Solar Energy Materials and Solar Cells, Vol. 65, No. 1-4, 2001, pp. 477-485. doi:10.1016/S0927-0248(00)00130-6
- R. B. Bergmann, “Crystalline Si Thin-Film Solar Cells: A Review,” Applied Physics A, Vol. 69, No. 2, 1999, pp. 187-194. doi:10.1007/s003390050989
- R. Brendel, “A Novel Process for Ultrathin Monocrystalline Silicon Solar Cells on Glass,” Proceeding of the 14th European Photovoltaic Solar Energy Conference, Barcelona, 6-10 June 1997, p. 1354.
- S. Huang, X. D. Ruan, J. Zou, X. Fu and H. Y. Yang, “Thermal Conductivity Measurement of SubmicrometerScale Silicon Dioxide Films by an Extended Micro-Raman Method,” Microsystem Technologies, Vol. 15, 2009, pp. 837-842
- G. Gesele, J. Linsmeier, V. Drach, J. Fricke and R. Arens-Fischer, “Temperature-Dependent Thermal Conductivity of Porous Silicon,” Journal of Physics D, Vol. 30, No. 21, 1997, p. 2911. doi:10.1088/0022-3727/30/21/001
- A. G. Nassiopoulou and G. Kaltsas, “Porous Silicon as an Effective Material for Thermal Isolation on Bulk Crystalline Silicon,” Physica Status Solidi A, Vol. 182, No. 1, 2000, pp. 307-311. doi:10.1002/1521-396X(200011)182:1<307::AID-PSSA307>3.0.CO;2-#
- V. Lysenko, S. Perichon, B. Remaki and D. Barbier, “Thermal Isolation in Microsystems with Porous Silicon,” Sensors and Actuators A, Vol. 99, No. 1-2, 2002, pp. 13-24. doi:10.1016/S0924-4247(01)00881-0
- P. Maccagnani, R. Angelucci, P. Pozzi, A. Poggi, L. Dori, G. C. Cardinali and P. Negrini, “Thick Oxidised Porous Silicon Layer as a Thermo-Insulating Membrane for High-Temperature Operating Thinand Thick-Film Gas Sensors,” Sensors and Actuators B, Vol. 49, No. 1-2, 1998, pp. 22-29. doi:10.1016/S0925-4005(97)00337-7
- C. Tsamis, A. Tserepi and A. G. Nassiopoulou, “Thermal Properties of Suspended Porous Silicon Micro-Hotplates for Sensor Applications,” Sensors and Actuators B, Vol. 95, No. 1-3, 2003, pp. 78-82. doi:10.1016/S0925-4005(03)00409-X
- S. M. Sze, “Physics of Semiconductor Devices,” John Wiley and Sons, New York, 1981, pp. 42-43.
- J. J. Yon, K. Barla, R. Herino and Bomchil, “The Kinetics and Mechanism of Oxide Layer Formation from Porous Silicon Formed on P-Si Substrates,” Journal of Applied Physics, Vol. 62, No. 3, 1987, pp. 1042-1048. doi:10.1063/1.339761
- Y. Arita and K. Kuranari, “Thermal Behavior of Porous Silicon,” Japanese Journal of Applied Physics, Vol. 15, 1976, pp. 1655-1664. doi:10.1143/JJAP.15.1655
- S. Huang, X.-D. Ruan, X. Fu, H.-Y. Yang and A. Majumdar, “Transient Ballistic and Diffusive Phonon Heat Transportin Thin Films,” Journal of Heat Transfer, Vol. 115, 1993, p. 7.
- A. A. Joshi and A. Majumdar, “Transient Ballistic and Diffusive Phonon Heat Transportin Thin Films,” Journal of Applied Physics, Vol. 74, No. 1, 1993, pp. 31-39.
- G. Chen, “Nonlocal and Nonequilibrium Heat Conduction in the Vicinity of Nanoparticles,” Journal of Heat Transfer, Vol. 118, No. 3, 1996, p. 539. doi:10.1115/1.2822665
- L. Roussel, B. Remaki, G. Delhomme, A. Dittmar and D. Barbier, “Study of Nano-Porous Silicon with Low Thermal Conductivity as Thermal Insulating Material,” Journal of Porous Materials, Vol. 7, No. 1-3, 2000, pp. 177-182. doi:10.1023/A:1009626518619
- Charles Populaire, These, lyon, 2005.
- A. Ould-Abbas, M. Bouchaour, M. Madani and N.-E. C. Sari, “Thermal Analysis and Morphological of Porous Silicon Oxidized or Not by Raman Spectroscopy,” Applications to Mems Thermal, Proceeding of Thermal French Congres, SFT 2006, Île de Ré, 16-19 Mai 2006.
- I. H. Campbell and P. M. Fauchet, “The Effects of Microcrystal Size and Shape on the One Phonon Raman Spectra of Crystalline Semiconductors,” Solid State Communications, Vol. 58, No. 10, 1986, pp. 739-741. doi:10.1016/0038-1098(86)90513-2
- M. Nonnenmacher and H. K. Wickramasinghe, “Scanning Probe Microscopy of Thermal Conductivity and Subsurface Properties,” Applied Physics Letters, Vol. 61, No. 2, 1992, pp. 168-170. doi:10.1063/1.108207

