Open Journal of Microphysics
Vol.08 No.03(2018), Article ID:86852,11 pages
10.4236/ojm.2018.83003
Non Hermitian Matrix Quasi-Exactly Solvable Hamiltonian
Ancilla Nininahazwe
Institut de Pédagogie Appliquée, Université du Burundi, Bujumbura, Burundi

Copyright © 2018 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: July 26, 2018; Accepted: August 21, 2018; Published: August 24, 2018
ABSTRACT
A new example of PT-symmetric quasi-exactly solvable (QES) -matrix Hamiltonian which is associated to a trigonometric Razhavi potential is considered. Like the QES analytic method considered in the Ref. [1][2], we establish three necessary and sufficient algebraic conditions for this Hamiltonian to have a finite-dimensional invariant vector space whose generic element is polynomial. This non hermitian matrix Hamiltonian is called quasi-exactly solvable [3].
Keywords:
PT-Symmetry, Razhavi potential, Quasi-Exact Solvability, QES Analytic Method

1. Introduction
Several problems in quantum physics lead to the main mathematical challenge of constructing the spectrum of a linear operator defined on an appropriate vector space of functions which belongs to a suitable domain of Hilbert space. In most cases, this type of problem cannot be analytically solved, in other words, all eigenvalues of the Hamiltonian cannot be computed algebraically. However, in few cases, the full spectrum of the Hamiltonians can be found in an analytical way because the potentials considered are exactly solvable. The one major example of this kind is the celebrated quantum Hamiltonian of the harmonic oscillator.
In the last few years, a new class of operators has been discovered. This class is intermediate between exactly solvable operators and non solvable operators. Its name is the quasi-exactly solvable (QES) operators [3]- [8], for which a finite part of the spectrum can be computed algebraically.
In the Ref. [1], PT-symmetric, QES -matrix Hamiltonians are analyzed with the emphasis set on the reality properties of the eigenvalues. The authors considered both trigonometric and hyperbolic -matrix Hamiltonians. A set of necessary and sufficient conditions (i.e. QES conditions) for -matrix operators to preserve a vector space of polynomials have been proposed. These QES conditions constitute the so-called QES analytic method.
This paper is organized as follows:
In the Section 2, based on the Ref. [1], we briefly recall the QES analytic method used to investigate the quasi-exact solvability of -matrix operators.
In the Section 3, we show in details that the trigonometric potential associated to the Razhavi Hamiltonian is non hermitian but it is invariant under the combined PT-symmetry.
In Section 4, along the same lines as in the Refs. [1][2], we apply the QES analytic method in order to construct a -matrix QES Hamiltonian depending on the trigonometric PT-invariant potential. The three necessary and sufficient QES conditions for the -matrix trigonometric Hamiltonian to have a finite dimensional invariant vector space will be obtained for two cases: and .
2. QES Analytic Method
Along the same lines as in the Refs. [1][2], we recall a general test to check whether a -matrix differential operator H (in a variable x) preserves a vector space whose components are polynomials is proposed.
Consider the -matrix operator of the following form [1][2]:
(1)
where
, , , ,
is the potential associated to the Hamiltonian H of the above relation (1).
A gauge transformation and a change of variable on the operator H lead to a new operator
(2)
which can be decomposed as follows
. (3)
More precisely, the diagonal components of are differential operators and
the off-diagonal components and are respectively proportional
to and . The operators and have lower degrees in all their components than the corresponding components in .
Note that the invariant vector space of the Hamiltonian has the following form [1][2]:
, and , (4)
where and denote respectively the polynomials of degree n and m in variable x.
In order to obtain the QES conditions for , the generic vector of the above vector space is of the form
, (5)
where are complex parameters. As a consequence the -matrices are defined by
,
,
. (6)
The three QES conditions for to have an invariant vector space are as follows
1) ,
2) ,
3) . (7)
In the next step, we will apply in a systematic way the previous QES analytic method in order to construct a -matrix QES Hamiltonian associated to a non hermitian and trigonometric potential.
3. PT-Symmetric QES Hamiltonian
In this section, we consider the non hermitian trigonometric -matrix Hamiltonian [1]:
, (8)
where are free real parameters.
The non diagonal elements are of the following forms [1]:
(9)
where C and are the independent coupling constants.
In the next step, we can show that the complex non hermitian -matrix potential associated to the above Hamiltonian given by the equation (8)
,
(10)
is invariant under the combined PT-symmetry, i.e. the following equality must be proved [1]:
(11)
Let us notice that under the time reflection operator T one replaces i by while under the parity operator P one replaces x by leading to
(12)
with
,
,
,
,
. (13)
Along the same above lines, one can easily check that
, and .
Now, we are allowed to write that
.
So, the potential is PT-symmetric. Indeed, it is this PT-invariant property requirement which explains the reality of some of the eigenvalues of the above trigonometric potential.
4. QES Non-Hermitian PT-Symmetric Hamiltonian
In this section, we apply the QES analytic method established previously (i.e. in the Section 2) to check whether the 2×2-matrix trigonometric Hamiltonian given by the Equation (8) is QES.
We consider the Hamiltonian H given by the Equation (8). In order to reveal the quasi-exact solvability of the trigonometric Hamiltonian H, it is convenient to perform the following change of function (i.e. the gauge transformation) according to [1]:
,
, (14)
where the gauge Hamiltonian can be written as follows
(15)
and the gauge function is of the following form
(16)
We must do the change in the variable z is as follows
(17)
in order to find the final form of the gauge Hamiltonian [1].
In the following, we will analyze in details the case and . In this case, the possible values for the parameters allow two algebraizations for the wave function, which can be written as follows:
Case 1: ,
Case 2: . (18)
Further choosing the parameter in the gauge function of the Equation (16) according to leads to the following components of the gauge Hamiltonian:
,
,
(19)
4.1. Case 1:
Taking account to the following values
and ,
the final form of the four components of the gauge Hamiltonian is obtained after some algebraic manipulations:
,
,
(20)
The gauge Hamiltonian can then be decomposed according to the Equation (3) of the QES analytic method as follows
(21)
with
(22)
One can easily check that the action of these above three components (of the gauge operator ) given by the Equation (22) on the wave function lead to the following relations
,
,
. (23)
After some algebraic manipulations, the -matrices can be obtained as follows [1][2]:
,
,
. (24)
Considering these above three relations (23) respectively, one can easily obtain the form of the three matrices as follows
,
,
The three necessary and sufficient QES conditions for the gauge Hamiltonian given by the Equation (19) to have a finite dimensional invariant vector space are successively obtained [1][2]:
1) The first QES condition is obtained as follows
,
,
,
(25)
2) The second QES condition is
,
,
(26)
3) Finally the third QES condition is found by the condition involving the matrix as follows
, (27)
where is a constant (i.e. one can choose ) and the first QES condition
leads to the following expression
(28)
Replacing the above expression (28) in the relation (27) and after some algebraic manipulations, one can easily find the third QES condition as
(29)
Note that referring to the three necessary and sufficient QES conditions given by the relations (25), (26) and (29), we can now conclude that the gauge Hamiltonian (therefore H) is quasi-exactly solvable. As a consequence, a finite part of the eigenvalues the Hamiltonian can be calculated algebraically.
4.2. Case 2:
This case can be analyzed along the same lines of the previous one.
Considering the gauge Hamiltonian given by the Equation (14) (i.e. the components of the gauge Hamiltonian given by the Equation (19)) and the same change variable of the previous case, the four elements of the -matrix gauge Hamiltonian take the following form
(30)
where and .
,
(31)
One can easily check that the action of these above three components of the gauge operator on the wave function lead to the following relations
,
,
. (32)
After some algebraic manipulations, the -matrices can be obtained as follows [1][2]:
,
,
. (33)
These above three relations (33) lead respectively to these following three matrices
,
,
Taking account to the conditions involving the three above matrices , i.e. along the same lines of the case 1, one can easily find the following three necessary and sufficient QES conditions for the gauge Hamiltonian given by the Equation (30) to have a finite dimensional invariant vector space [1][2]:
1) The first QES condition is
(34)
2) The second QES condition is as follows
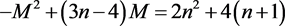 (35)
(35)
3) The final and the third QES condition is
 (36)
(36)
As the three necessary and sufficient QES conditions given by the relations (34), (35) and (36), we can now conclude that the gauge Hamiltonian 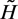 given by the relation (30) is quasi-exactly solvable. It means that the gauge Hamiltonian
given by the relation (30) is quasi-exactly solvable. It means that the gauge Hamiltonian 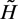 has a finite dimensional vector space which is invariant under its action.
has a finite dimensional vector space which is invariant under its action.
In other words, a finite part of the eigenvalues the Hamiltonian 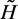 can be calculated algebraically [1]- [8].
can be calculated algebraically [1]- [8].
5. Conclusion
In this paper, we have applied the QES analytic method established in the Ref. [1]in order to construct a 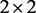 -matrix QES Hamiltonian which is associated to a potential depending on the trigonometric functions. We have considered two cases for the wave function:
-matrix QES Hamiltonian which is associated to a potential depending on the trigonometric functions. We have considered two cases for the wave function: 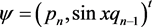 and
and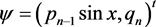 . The three necessary and sufficient QES conditions for the non hermitian
. The three necessary and sufficient QES conditions for the non hermitian 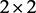 -matrix trigonometric Hamiltonian to have a finite vector space invariant under its action are computed algebraically [1][2].
-matrix trigonometric Hamiltonian to have a finite vector space invariant under its action are computed algebraically [1][2].
Acknowledgements
I thank Pr. Yves Brihaye of useful discussions.
Conflicts of Interest
The authors declare no conflicts of interest regarding the publication of this paper.
Cite this paper
Nininahazwe, A. (2018) Non Hermitian Matrix Quasi-Exactly Solvable Hamiltonian. Open Journal of Microphysics, 8, 15-25. http://dx.doi.org/10.4236/ojm.2018.83003
References
- 1. Brihaye, Y., Nininahazwe, A. and Mandal, B.P. (2007) PT-Symmetric, Quasi-Exactly Solvable Matrix Hamiltonians. Journal of Physics A: Mathematical and Theoretical, 40, 13063-13073. https://doi.org/10.1088/1751-8113/40/43/014
- 2. Nininahazwe, A. (2013) Matrix Quasi-Exactly Solvable Jacobi Elliptic Hamiltonian. Open Journal of Microphysics (OJM), 3, 53-59. https://doi.org/10.4236/ojm.2013.33010
- 3. Turbiner, A.V. (1988) Quasi-Exactly Solvable Problems and sl(2) Algebra. Communications in Mathematical Physics, 118, 467-474. https://doi.org/10.1007/BF01466727
- 4. Ushveridze, A.G. (1995) Quasi-Exactly Solvable Models in Quantum Mechanics. Institute of Physics Publishing.
- 5. Turbiner, A.V. (1989) Lamé Equation sl(2) Algebra and Isospectral Deformations. Journal of Physics A: Mathematical and General, 22, L1-L3. https://doi.org/10.1088/0305-4470/22/1/001
- 6. Shifman, M.A. and Turbiner, A.V. (1989) Quantal Problems with Partial Algebriazation of the Spectrum. Communications in Mathematical Physics, 126, 347-365. https://doi.org/10.1007/BF02125129
- 7. Brihaye, Y. and Kosinski, P. (1997) Quasi-Exactly Solvable Matrix Models in sl(n). Physics Letters B, 424, 43-47. https://doi.org/10.1016/S0370-2693(98)00167-1
- 8. Brihaye, Y. and Hartmann, B. (2001) Quasi-Exactly Solvable -Matrix Schr?dinger Operators. Modern Physics Letters A, 16, 1895-1906. https://doi.org/10.1142/S0217732301005242

