Received 11 February 2015; accepted 25 March 2015; published 26 March 2015

ABSTRACT

We make a rigorous exploration of the profiles of a few diagonal and off-diagonal components of linear (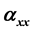, , 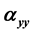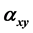and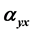), first nonlinear (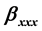, , 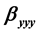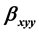and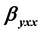), and second nonlinear (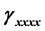, , 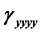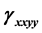and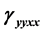) polarizabilities of quantum dots under the influence of external pulsed field. Simultaneous presence of additive white noise has also been considered. The quantum dot contains dopant described by a Gaussian potential. The numbers of pulse and the dopant location have been found to fabricate the said profiles jointly. The 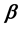components display greater complexity in their profiles in comparison with the 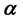and 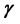counterparts. 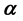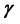The presence of noise prominently enhances the influence of dopant coordinate on the polarizability profiles, particularly for and components. However, for components, the said influence becomes quite evident both in the presence and absence of additive noise. The study reveals some means of achieving stable, enhanced, and often maximized output of noise-driven linear and nonlinear polarizabilities.

Keywords:

Quantum Dot, Impurity, Polarizability, Pulsed Field, Dopant Location, Additive White Noise

1. Introduction

The nonlinear optical effects displayed by Quantum dots (QDs) are enriched with much more subtleties than the bulk materials. As a result QDs have found a broad range of application in a variety of optical devices. Incorporation of dopants to QDs causes a drastic change in the properties of the latter. The change happens because of the interplay between the intrinsic dot confinement potential and the dopant potential. We thus find a rich variety of useful investigations on doped QD [1] -[9] . From the perspective of optoelectronic applications, impurity driven modulation of linear and nonlinear optical properties is highly important in photodetectors and in several high-speed electro-optical devices [10] . Naturally, researchers have carried out a lot of important works on both linear and nonlinear optical properties of these structures [10] -[29] .

External electric field often highlights important features arising out of the confined impurities. The electric field changes the energy spectrum of the carrier and thus influences the performance of the optoelectronic devices. In addition, the electric field often lifts the symmetry of the system and promotes emergence of nonlinear optical properties. Thus, the applied electric field possesses special importance in the field of research on the optical properties of doped QDs [30] -[42] .

Recently we have made extensive investigations of the role of noise on the linear and nonlinear polarizabilities of impurity doped QDs [43] -[45] . In the present work we have explored some of the diagonal and off-di- agonal components of linear (, , and), second order (, , and), and third order (, , and) polarizabilities of quantum dots in presence of Gaussian white noise introduced additively to the system. The doped system is exposed to an external pulsed electric field. The diagonal and off-diagonal components are expected to behave diversely because of their varied interactions with the pulsed field and noise. We have found that the number of pulses delivered to the system from the external field and the dopant coordinate contribute significantly in designing the various polarizability components. A change in in effect changes the amount of energy delivered to the doped system. And the role of dopant site has been given special importance following the notable works of Karabulut and Baskoutas [24] , Baskoutas et al. [30] , and Khordad and Bahramiyan [28] in the context of optical properties of doped heterostructures. The present enquiry addresses the important roles played by and in fabricating the various polarizability components in presence of additive noise.

2. Method

The Hamiltonian corresponding to a 2-d quantum dot with single carrier electron laterally confined (parabolic) in the x-y plane and doped with a Gaussian impurity is given by

(1)

where is the Hamiltonian in absence of impurity. Under the effective mass approximation it reads

. (2)

The confinement potential reads with harmonic confinement frequency and the effective mass. The value of has been chosen to be resembling GaAs quantum dots. We have set and perform our calculations in atomic unit. The parabolic confinement potential has been utilized in the study of optical properties of doped QDs by Çakir et al. [17] [18] . Recently Khordad and his coworkers introduced a new type of confinement potential for spherical QD’s called Modified Gaussian Potential, MGP [46] [47] . A perpendicular magnetic field (B ~ mT) serves as an additional confinement. In Landau gauge

(A being the vector potential), the Hamiltonian transforms to

(3)

being the cyclotron frequency and can be viewed as the effective frequency in the y-direction. being the impurity (dopant) potential (Gaussian) [48] -[50] and is given by

(4)

Positive values for and indicate a repulsive impurity., and represent the impurity potential, the dopant coordinate, and the spatial stretch of impurity, respectively.

We have employed a variational recipe to solve the time-independent Schrodinger equation and the trial function has been constructed as a superposition of the product of harmonic oscillator eigenfunctions and respectively, as

(5)

where are the variational parameters and and. In the linear variational calculation, requisite number of basis functions have been exploited after performing the convergence test. And is diagonalized in the direct product basis of harmonic oscillator eigenfunctions.

The external pulsed field can be represented by

(6)

is the time-dependent field intensity modulated by a pulse-shape function where the pulse has a peak field strength, and a fixed frequency. The pulsed field is applied along both and directions. In the present work we have invoked a sinusoidal pulse give by

(7)

where stands for pulse duration time. Thus, or equivalently (the number of pulses), appears to be a key control parameter. Figure 1 depicts the profiles of five consecutive sinusoidal pulses as a function of time. With the application of pulsed field the time dependent Hamiltonian becomes

(8)

where

(9)

In presence of additive white noise the time-dependent Hamiltonian becomes

(10)

where is the noise term that follows a Gaussian distribution with characteristics [43] -[45] :

, (11)

and

, (12)

where tands for the noise strength.

The evolving wave function can now be described by a superposition of the eigenstates of, i.e.

(13)

The time-dependent Schrödinger equation (TDSE) carrying the evolving wave function has now been solved numerically by 6-th order Runge-Kutta-Fehlberg method with a time step size a.u. after verifying the numerical stability of the integrator. The time dependent superposition coefficients has been used to calculate the time-average energy of the dot. We have determined the energy eigenvalues for various combinations of field intensities and used them to compute some of the diagonal and off-diagonal components of linear and nonlinear polarizabilities by the following relations obtained by numerical differentiation. For linear polarizability.

(14)

And a similar expression for.

(15)

and a similar expression for computing component.

The components of first nonlinear polarizability (second order/quadratic hyperpolarizability) are calculated from following expressions

(16)

and a similar expression is used for computing component.

(17)

and a similar expression for computing component.

The components of second nonlinear polarizability (third order/cubic hyperpolarizability) are given by

(18)

and a similar expression is used for computing component.

(19)

and a similar expression is used for computing component.

3. Results and Discussion

At the very onset of discussion it needs to be mentioned that the presence of additive noise changes the profiles of various polarizability components from that of noise-free condition. The magnitude of the components also increases invariably because of enhanced dispersive character of the system. However, in keeping with our previous findings a change in noise strength does not that much affect the outcomes [43] -[45] .

3.1. Linear and Second Nonlinear Polarizability Components

Figure 2(a) depicts the profiles of component with variation of for on-center, near off-center, and far off-center dopant locations, respectively. The plots exhibit different behaviors as is varied depending on the dopant location. For an on-center dopant minimizes at [Figure 2(a) (i)] whereas for a near off-center dopant we observe maximization of the said component nearly at the same value [Figure 2(a) (ii)]. The profile takes a new pattern for a far off-center dopant when increases monotonically with up to after which it saturates with further increase in [Figure 2(a) (iii)]. It therefore comes out that the interplay between and noticeably affects the profile of component and the interplay becomes most prominent at a typical pulse number of. The role of additive noise will be clear if we make a look at the said profile under noise-free condition. We have found that at that condition exhibits a profile similar to that of Figure 2(a) (iii) at all dopant locations. Thus, it can be inferred that the introduction of additive noise makes the role of more conspicuous. The other diagonal component evinces almost similar profile. Figure 2(b) displays the similar plot for the off-diagonal component. Firstly, we find a reduction (by a factor of ~10²) in the value of in comparison with its diagonal counterpart. Moreover, the pattern of variation of the polarizability component shows considerable deviation from that of the diagonal one. For an on-center dopant falls steadily with increase in up to beyond which it saturates [Figure 2(b) (i)]. The pattern gets changed with near and far off-center dopants while exhibits some initial steady behavior till after which it rises considerably up to followed by saturation thereafter [Figure 2(b) (ii) and Figure 2(b) (iii)]. As before, absence of additive noise downplays the role of dopant site. The absence makes profile look like that of Figure 2(b) (i) at all dopant locations. The off-diagonal component displays quite similar behavior.

Figure 3 depicts the similar profile for diagonal [(i) to (iii)] and off-diagonal [(iv) to (vi)] compnents. For on-center and near off-center dopants exhibits minima at [Figure 3 (i) and Figure 3 (ii)].

However, for a far off-center dopant decreases smoothly up to and settles thereafter [Figure 3 (iii)]. As we have observed for, here also absence of additive noise scraps any influence of dopant site on the component. The other diagonal component behaves similarly. With an on-center dopant the off-diagonal component behaves quite similar to that of diagonal component with a far off-center dopant [Figure 3 (iv)]. With near and far off-center dopants exhibits a different behavior from that of on- center one. In both these cases, the said component increases with steadily up to beyond which they saturate [Figure 3 (v) and Figure 3 (vi)]. The other off-diagonal component does not show any appreciable alteration in its behavior. Interestingly, unlike the diagonal component, exhibits noticeable dependence on dopant site even in the absence of additive noise. However, the said dependence follows just the reverse pattern of what we have found here in the presence of noise [Figure 3 (iv)-(vi)].

3.2. First Nonlinear Polarizability Components

The inversion symmetry of the Hamiltonian [cf. Equation (3)] is preserved in the presence of an on-center dopant which annihilates the emergence of all components under noise-free condition. In absence of noise, the emergence of components has been observed only for off-center dopants. The additive noise changes the scenario and we find profiles of components at all dopant locations. However, the magnitude of the components enhances by a factor of ~10⁵ for off-center dopants in comparison with the on-center analog. The additive noise, therefore, partially reduces the symmetry of the system.

Figure 4(a) represents the profiles of diagonal and components [(i) and (ii)] and off-diagonal and components [(iii) and (iv)] as a function of for an on-center dopant. and show minimization at [Figure 4(a) (i)] and [Figure 4(a) (ii)], respectively. exhibits steady behavior up to [Figure 4(a) (iii)] and then rises prominently., on the other hand, rises smoothly till and saturates henceforth [Figure 4(a) (iv)].

Figure 4(b) represents the similar plots for a near off-center dopant. has been found to decrease steadily up to beyond which it saturates [Figure 4(a) (i)]. component exhibits maximization at [Figure 4(a) (ii)]. displays a pattern resembling that of and saturates at [Figure 4(a) (iii)]. component depicts a minimization at [Figure 4(a) (iv)]. In absence of additive noise, we get somewhat different profiles for above components at the same dopant location.

Figure 4(c) delineates the analogous plots for a far off-center dopant. depicts almost similar pattern [Figure 4(c) (i)] as in case of near off-center dopant; the only difference being that it now saturates at (instead of as in previous case). also, as before, exhibits maximization at [Figure 4(c) (ii)] (instead of as in previous case). component shows minimization at [Figure 4(c) (iii)]. component initially exhibits a steady value up to, after which it rises sharply and culminates in saturation at [Figure 4(c) (iv)].

Thus, it turns out that both dopant location and the number of pulses affect the polarizability profiles with sufficient delicacy. Particularly, the importance of dopant site in the present work complies with other notable works which manifest the contribution of dopant location in designing various properties of mesoscopic systems. In this context the works of Sadeghi and Avazpour [4] [5] , Yakar et al. [7] , Xie [9] , Karabulut and Baskoutas [24] , Khordad and Bahramiyan [28] , and Baskoutas and his co-workers [30] deserve proper mention.

4. Conclusion

A few diagonal and off-diagonal components of linear, first nonlinear, and second nonlinear polarizabilities of impurity doped quantum dots have been explored under the influence of a pulsed field and in the presence of additive noise. The number of pulses fed into the system as well as the dopant location noticeably fabricates the polarizability profiles. It has been noticed that the components behave in a visibly different fashion from and components under pulsed field. Moreover, the components offer greater delicacy with variation of as well as dopant site. The pulsed field thus modulates the second-order polarizability more sensitively than the linear and third-order polarizabilities. Whereas a variation in directly monitors the energy input from the external field, a varying modulates the spatial distribution of energy levels internally through different extents of dot-impurity interaction. Absence of additive noise diminishes the influence of dopant location on linear polarizability components; most prominently, on third-order polarizability components; somewhat less prominently. However, for second-order polarizability components, dopant location plays a significant role both in the presence and absence of additive noise, though in noticeably diverse manners. The study indicates some genuine pathways of achieving enhanced, maximized and often stable linear and nonlinear polarizabilities of doped QD in presence of additive noise which could be important in the field of noise-driven optical properties of these systems.

References