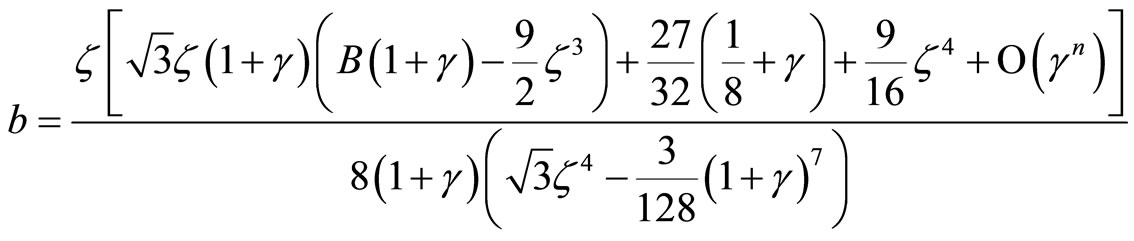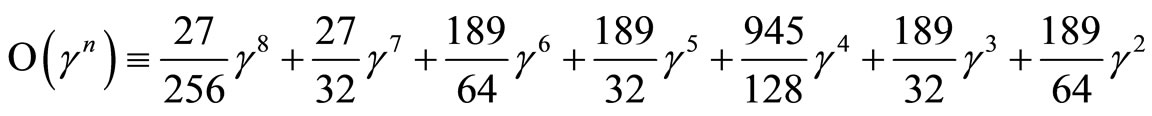Open Journal of Microphysics
Vol.4 No.1(2014), Article ID:42940,5 pages DOI:10.4236/ojm.2014.41001
A Toy Model of Universe
1Physics Department, Ilam Branch, Islamic Azad University, Ilam, Iran
2Iran Department of Physics, Ilam Branch, Islamic Azad University, Ilam, Iran
3Young Researchers and Elite Club, Islamic Azad University, Mahabad, Iran
Email: naji.jalil2020@gmail.com
Copyright (c) 2014 J. Naji et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights (c) 2014 are reserved for SCIRP and the owner of the intellectual property J. Naji et al. All Copyright (c) 2014 are guarded by law and by SCIRP as a guardian.
Received November 25, 2013; revised December 25, 2013; accepted January 2, 2014
Keywords:FRW Cosmology; Modified Chaplygin Gas; Bulk Viscosity
ABSTRACT
In this paper, we suggest that a toy model of our universe is based on FRW bulk viscous cosmology in presence of modified Chaplygin gas. We obtain modified Friedman equations due to bulk viscosity and Chaplygin gas and calculate time-dependent energy density for the special case of flat space.
1. Introduction
It is found that our universe expands with acceleration [1-5]. The accelerating expansion of the universe may be explained in context of the dark energy [6]. Due to negative pressure, the simplest way for modeling the dark energy is the Einstein’s cosmological constant. On the other hand, the study of the cosmological constant is one of the important subjects in the theoretical and experimental physics [7-10]. Another candidate for the dark energy is scalarfield dark energy model [11-19]. However, presence of a scalar field is not only requirement of the transition from a universe filled with matter to an exponentially expanding universe. Therefore, Chaplygin gas is used as an exotic type of fluid, which is based on the recent observational fact that the equation of state parameter for dark energy can be less than −1.
On the other hand, we know that the viscosity plays an important role in the cosmology [20]. In another word, the presence of viscosity in the fluid introduces many interesting pictures in the dynamics of homogeneous cosmological models, which is used to study the evolution of universe. In Ref. [21], the exact solutions of the field equations for a five-dimensional space-time with viscous fluid were obtained. Also in Ref. [22] a cosmological model with viscous fluid in higher-dimensional spacetime was constructed. Then, in Ref. [23] the exact solutions of the field equations for a five-dimensional cosmological model with variable bulk viscosity were obtained. The isotropic homogeneous spatially flat cosmological model with bulk viscous fluid was constructed in Ref. [24]. The bulk viscous cosmological models with constant bulk viscosity coefficient were constructed in Ref. [25]. In the recent work [26] the FRW bulk viscous cosmology was considered and bulk viscous coefficient was obtained in the flatspace, and then extended to non-flat space [27]. In this work, we consider both bulk viscous effect and Chaplygin gas in FRW cosmology in flat space.
2. Equations
The Friedmann-Robertson-Walker (FRW) universe in four-dimensional space-time is described by the following metric [28,29],
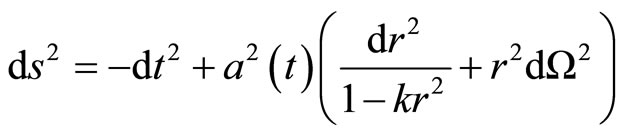 (1)
(1)
where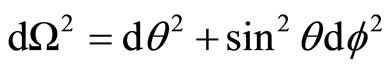 , and
, and  represents the scale factor. The
represents the scale factor. The 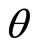 and
and 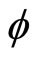 are the usual azimuthal and polar angles of spherical coordinates. Also, constant
are the usual azimuthal and polar angles of spherical coordinates. Also, constant 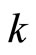 denotes the curvature of the space. In this paper we consider the case of
denotes the curvature of the space. In this paper we consider the case of  only, which is corresponding to flat space. In that case the Einstein equation is given by,
only, which is corresponding to flat space. In that case the Einstein equation is given by,
 (2)
(2)
where we assumed 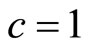 and
and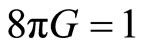 . Also the energy-momentum tensor corresponding to the bulk viscous fluid and modified Chaplygin gas [30-35] is given by the following relation,
. Also the energy-momentum tensor corresponding to the bulk viscous fluid and modified Chaplygin gas [30-35] is given by the following relation,
 (3)
(3)
where  is the energy density and
is the energy density and  is the velocity vector with normalization condition
is the velocity vector with normalization condition . Also, the total pressure and the proper pressure involve bulk viscosity coefficient
. Also, the total pressure and the proper pressure involve bulk viscosity coefficient  and Hubble expansion parameter
and Hubble expansion parameter 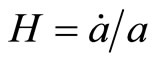 are given by the following equations [36-42],
are given by the following equations [36-42],
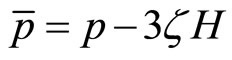 (4)
(4)
and,
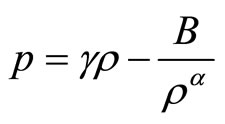 (5)
(5)
with  and
and . The equation of state
. The equation of state  is one of the most important quantity to describe the features of dark energy models. It is clear that the parameter
is one of the most important quantity to describe the features of dark energy models. It is clear that the parameter  shows bulk viscosity and B shows effect of Chaplygin gas. In the Ref. [43] the dynamics of FRW cosmology with modified Chaplygin gas as the matter formulated. Then the nature of the critical points are studied by evaluating the eigenvalues of the linearized Jacobi matrix for the special case of
shows bulk viscosity and B shows effect of Chaplygin gas. In the Ref. [43] the dynamics of FRW cosmology with modified Chaplygin gas as the matter formulated. Then the nature of the critical points are studied by evaluating the eigenvalues of the linearized Jacobi matrix for the special case of . In this paper we consider special case with
. In this paper we consider special case with  and extend the Ref. [43] to including bulk viscous coefficient.
and extend the Ref. [43] to including bulk viscous coefficient.
In that case the Friedmann equations are given by,
 (6)
(6)
and,
 (7)
(7)
where dot denotes derivative with respect to cosmic time . The energy-momentum conservation law obtained as the following,
. The energy-momentum conservation law obtained as the following,
 (8)
(8)
In the next section we try to obtain time-dependent density by using above equations.
3. Solutions
Using the Equations (4)-(6) in the conservation relation (8) we have,
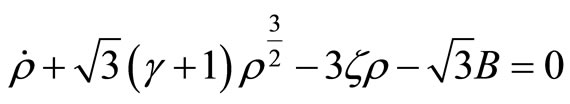 (9)
(9)
If we set , then one can extract energy density depend on scale factor [43],
, then one can extract energy density depend on scale factor [43],
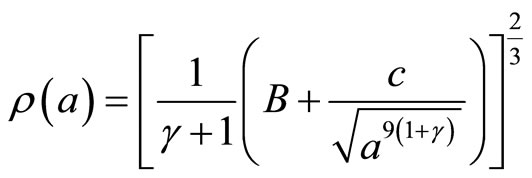 (10)
(10)
where c is an integration constant. Here we also consider bulk viscous coefficient and would like to obtain energy density depend on time. In order to solve Equation (9) we use the following ansatz,
 (11)
(11)
where constants ,
, 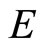 ,
,  ,
, 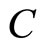 and
and 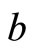 should be determined. Substituting relation (11) in the Equation (9) gives us the following coefficients,
should be determined. Substituting relation (11) in the Equation (9) gives us the following coefficients,
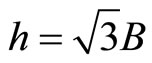 (12)
(12)
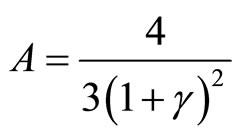 (13)
(13)
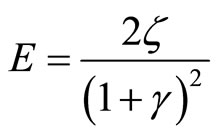 (14)
(14)
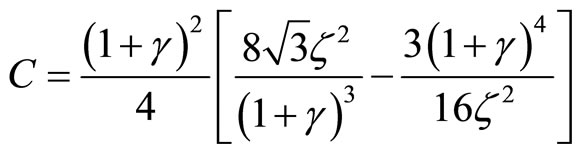 (15)
(15)
If we neglect both bulk viscosity and presence of Chaplygin gas then,
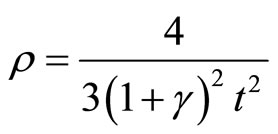 (18)
(18)
which is agree with results of the Refs. [27,43] where  established. On the other hand for the large bulk viscosity coefficient one can find that
established. On the other hand for the large bulk viscosity coefficient one can find that 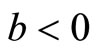 and hence
and hence 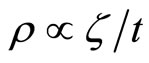 obtained. Also for the case of infinitesimal
obtained. Also for the case of infinitesimal 
| where, |
one can obtain constant negative energy density. In the general case, Equation (11) with coefficients (12)-(16) tells us that the energy density is decreasing function of time. Such behavior happen for the Hubble expansion parameter which is discussed below.
By using time-dependent density in the relation (6) one can obtain Hubble expansion parameter. In that case we draw plot of Hubble expansion parameter in the Figure 1 for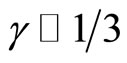 .
.
In that case the modified Chaplygin gas model describes the evolution of the universe from the radiation regime to the Λ-cold dark matter scenario, where the fluid behaves as a cosmological constant, so there is an accelerated expansion of the universe.
It is possible to study deceleration parameter of this theory which obtained by the following relation,
 (19)
(19)
Numerically we draw deceleration parameter in terms of time in the Figure 2.
4. Conclusions
In this work, we studied the FRW bulk viscous cosmology with modified Chaplygin gas as the matter contained. We obtained the modified Friedmann equations due to bulk viscous and Chaplygin gas coefficients. Then tried to solve equations and found time-dependent energy density. Therefore, we could extract Hubble expansion and deceleration parameters.

Figure 1. Hubble expansion parameter in terms of time for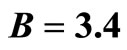 ,
, 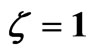 , and
, and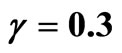 .
.
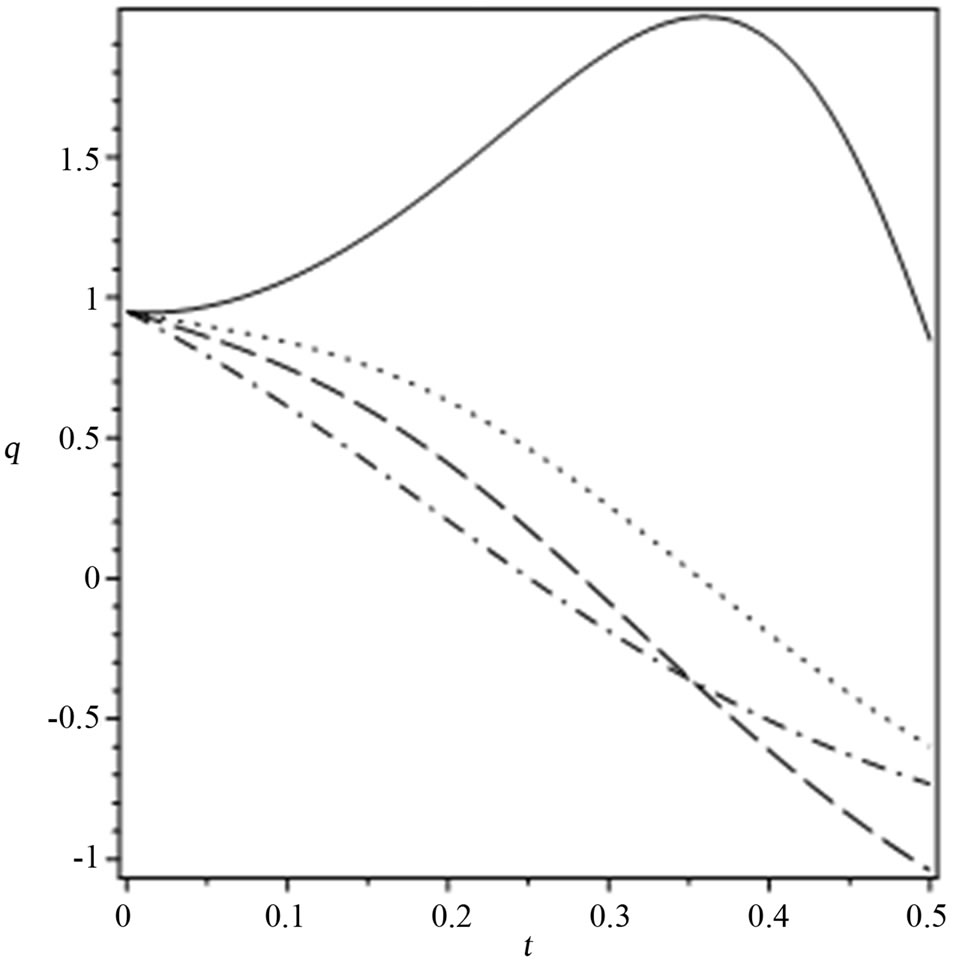
Figure 2. Deceleration parameter in terms of time for  and
and . Solid, dotted, dashed and dash dotted lines represent
. Solid, dotted, dashed and dash dotted lines represent  respectively.
respectively.
For the future work, it is possible to repeat calculation of this paper for the case of arbitrary α or non-flat universe where . In that case one deals with the following equation,
. In that case one deals with the following equation,
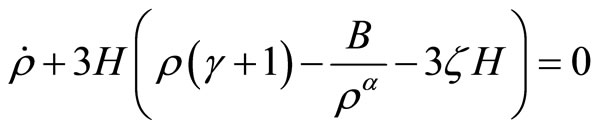 (20)
(20)
where .
.
REFERENCES
- A. G. Riess, et al., “Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant,” The Astronomical Journal, Vol. 116, No. 3, 1998, pp. 1009-1038. http://dx.doi.org/10.1086/300499
- S. Perlmutter, et al., “Measurements of Ω and Λ from 42 High-Redshift Supernovae,” The Astronomical Journal, Vol. 517, No. 2, 1999, pp. 565-586. http://dx.doi.org/10.1086/307221
- R. A. Knop, et al., “New Constraints on ΩM, ΩΛ, and w from an Independent Set of Eleven High-Redshift Supernovae Observed with HST,” The Astronomical Journal, Vol. 598, No. 1, 2003, p. 102. http://dx.doi.org/10.1086/378560
- A. G. Riess, et al., “Type Ia Supernova Discoveries at z > 1 from the Hubble Space Telescope: Evidence for Past Deceleration and Constraints on Dark Energy Evolution,” The Astronomical Journal, Vol. 607, 2004, pp. 665-687. http://dx.doi.org/10.1086/383612
- C. L. Bennet, et al., “First-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Preliminary Maps and Basic Results,” The Astrophysical Journal Supplement Series, Vol. 148, 2003, p. 1. http://dx.doi.org/10.1086/377253
- K. Bamba, S. Capozziello, S. Nojiri and S. D. Odintsov, “Dark Energy Cosmology: The Equivalent Description via Different Theoretical Models and Cosmography Tests,” Astrophysics and Space Science, Vol. 342, 2012, pp. 155- 228.
- S. M. Carroll, “The Cosmological Constant,” Living Reviews in Relativity, Vol. 3, 2001, p. 1.
- T. Padmanabhan, “Cosmological Constant—The Weight of the Vacuum,” Physics Reports, Vol. 380, No. 5-6, 2003, pp. 235-320. http://dx.doi.org/10.1016/S0370-1573(03)00120-0
- P. J. E. Peebles and B. Ratra, “The Cosmological Constant and Dark Energy,” Reviews of Modern Physics, Vol. 75, No. 2, 2003, pp. 559-606. http://dx.doi.org/10.1103/RevModPhys.75.559
- S. Nobbenhuis, “Categorizing Different Approaches to the Cosmological Constant Problem,” Foundations of Physics, Vol. 36, No. 5, 2006, pp. 613-680. http://dx.doi.org/10.1007/s10701-005-9042-8
- P. J. E. Peebles and B. Ratra, “Cosmology with A TimeVariable Cosmological ‘Constant’,” The Astronomical Journal, Vol. 325, 1988, pp. L17-L20. http://dx.doi.org/10.1086/185100
- B. Ratra and P. J. E. Peebles, “Cosmological Consequences of a Rolling Homogeneous Scalar Field,” Physical Review D, Vol. 37, No. 12, 1988, pp. 3406-3427. http://dx.doi.org/10.1103/PhysRevD.37.3406
- M. S. Turner and M. J. White, “CDM Models with a Smooth Component,” Physical Review D, Vol. 56, No. 8, 1997, pp. 4439-4443. http://dx.doi.org/10.1103/PhysRevD.56.R4439
- R. R. Caldwell, “A Phantom Menace? Cosmological Consequences of a Dark Energy Component with Super-Negative Equation of State,” Physics Letters B, Vol. 545, No. 1-2, 2002, pp. 23-29. http://dx.doi.org/10.1016/S0370-2693(02)02589-3
- A. Sen, “Tachyon Matter,” Journal of High Energy Physics, Vol. 2002. http://dx.doi.org/10.1088/1126-6708/2002/07/065
- B. Feng, X. L. Wang and X. M. Zhang, “Dark Energy Constraints from the Cosmic Age and Supernova,” Physics Letters B, Vol. 607, No. 1-2, 2005, pp. 35-41. http://dx.doi.org/10.1016/j.physletb.2004.12.071
- Z. K. Guo, Y. S. Piao, X. M. Zhang and Y. Z. Zhang, “Cosmological Evolution of a Quintom Model of Dark Energy,” Physics Letters B, Vol. 608, No. 3-4, 2005, pp. 177-182. http://dx.doi.org/10.1016/j.physletb.2005.01.017
- H. Wei and R. G. Cai, “Cosmological Evolution of ‘Hessence’ Dark Energy and Avoidance of the Big Rip,” Physical Review D, Vol. 72, No. 12, 2005, Article ID: 123507. http://dx.doi.org/10.1103/PhysRevD.72.123507
- H. Wei, N. N. Tang and R. G. Cai, “Reconstruction of Hessence Dark Energy and the Latest Type Ia Supernovae Gold Dataset,” Physical Review D, Vol. 75, No. 4, 2007, Article ID: 043009. http://dx.doi.org/10.1103/PhysRevD.75.043009
- N. Ibotombi Singh and S. Romaleima Devi, “A New Class of Bulk Viscous FRW Cosmological Models in a Scale Covariant Theory of Gravitation,” Astrophysics and Space Science, Vol. 334, No. 2, 2011, pp. 231-236. http://dx.doi.org/10.1007/s10509-011-0739-1
- S. Chatterjee and B. Bhui, “Viscous Fluid in a KaluzaKlein Metric,” Astrophysics and Space Science, Vol. 167, No. 1, 1990, pp. 61-67. http://dx.doi.org/10.1007/BF00642063
- A. Banergee, B. Bhui and S. Chatterjee, “Bianchi Type-I Cosmological Models in Higher Dimensions,” The Astronomical Journal, Vol. 358, 1990, pp. 23-27.
- G. P. Singh, R. V. Deshpande and T. Singh, “HigherDimensional Cosmological Model with Variable Gravitational Constant and Bulkviscosity in Lyra Geometry,” Pramana, Vol. 63, No. 5, 2004, pp. 937-945. http://dx.doi.org/10.1007/BF02704332
- G. L. Murphy, “Big-Bang Model without Singularities,” Physical Review D, Vol. 8, No. 12, 1973, pp. 4231-4233. http://dx.doi.org/10.1103/PhysRevD.8.4231
- R. Bali and S. Dave, “Viscous Cosmological Models with Particle Creation in Brans-Dicke Theory,” Astrophysics and Space Science, Vol. 282, No. 2, 2002, pp. 461-466. http://dx.doi.org/10.1023/A:1020834610024
- S. D. Katore, A. Y. Shaikh, D. V. Kapse and S. A. Bhaskar, “FRW Bulk Viscous Cosmology in Multi Dimensional Space-Time,” International Journal of Theoretical Physics, Vol. 50, No. 9, 2011, pp. 2644-2654. http://dx.doi.org/10.1007/s10773-011-0760-8
- H. Saadat, “FRW Bulk Viscous Cosmology in Non-Flat Universe,” International Journal of Theoretical Physics, Vol. 51, No. 5, 2012, pp. 1317-1322. http://dx.doi.org/10.1007/s10773-011-1007-4
- B, Saha, H. Amirhashchi and A. Pradhan, “Two-Fluid Scenario for Dark Energy Models in an FRW UniverseRevisited,” Astrophysics and Space Science, Vol. 342, No. 1, 2012, pp. 257-267. http://dx.doi.org/10.1007/s10509-012-1155-x
- M. Jamil, D. Momeni, N. S. Serikbayev and R. Myrzakulov, “FRW and Bianchi Type I Cosmology of f-Essence,” Astrophysics and Space Science, Vol. 339, No. 1, 2012, pp. 37-43. http://dx.doi.org/10.1007/s10509-011-0964-7
- J. Sadeghi, M. Khurshudyan, B. Pourhassan and H. Farahani, “Time-Dependent Density of Modified Cosmic Chaplygin Gas with Cosmological Constant in Non-Flat Universe,” IJTP, 2014.
- U. Debnath, A. Banerjee and S. Chakraborty, “Role of Modified Chaplygin Gas in Accelerated Universe,” Classical and Quantum Gravity, Vol. 21, 2004, pp. 5609-5618. http://dx.doi.org/10.1088/0264-9381/21/23/019
- Y. D. Xu, Z. G. Huang and X. H. Zhai, “A New Type of Interaction between Generalized Chaplygin Gas and Dark Matter,” Astrophysics and Space Science, Vol. 339, No. 1, 2012, pp. 31-36. http://dx.doi.org/10.1007/s10509-012-0974-0
- T. Bandyopadhyay, “Thermodynamics of Gauss-Bonnet Brane with Modified Chaplygin Gas,” Astrophysics and Space Science, Vol. 341, No. 2, 2012, pp. 689-693. http://dx.doi.org/10.1007/s10509-012-0974-0
- P. Rudra, U. Debnath and R. Biswas, “Dynamics of Modified Chaplygin Gas in Brane World Scenario: Phaseplane Analysis,” Astrophysics and Space Science, Vol. 339, No. 1, 2012, pp. 53-64. http://dx.doi.org/10.1007/s10509-011-0967-4
- P. Rudra, “Dynamics of Interacting Generalized Cosmic Chaplygin Gas in Brane-World Scenario,” Astrophysics and Space Science, Vol. 342, No. 2, 2012, pp. 579-599. http://dx.doi.org/10.1007/s10509-012-1198-z
- H. Saadat and B. Pourhassan, “Effect of Varying Bulk Viscosity on Generalized Chaplygin Gas,” International Journal of Theoretical Physics, 2013.
- J. Naji, B. Pourhassan and A. R. Amani, “Effect of Shear and Bulk Viscosities on Interactingmodified Chaplygin Gas Cosmology,” International Journal of Modern Physics D, 2013.
- H. Saadat and B. Pourhassan, “Viscous Varying Generalized Chaplygin Gas with Cosmological Constant and Space Curvature,” International Journal of Theoretical Physics, Vol. 52, 2013, pp. 3712-3720.
- B. Pourhassan, “Viscous Modified Cosmic Chaplygin Gas Cosmology,” International Journal of Modern Physics D, Vol. 22, No. 9, 2013, Article ID: 1350061. http://dx.doi.org/10.1142/S0218271813500612
- A. R. Amani and B. Pourhassan, “Viscous Generalized Chaplygin Gas with Arbitrary α,” International Journal of Theoretical Physics, Vol. 52, No. 4, 2013, pp. 1309- 1313. http://dx.doi.org/10.1007/s10773-012-1446-6
- H. Saadat and B. Pourhassan, “FRW Bulk Viscous Cosmology with Modified Cosmic Chaplygin Gas,” Astrophysics and Space Science, Vol. 344, No. 1, 2013, pp. 237-241. http://dx.doi.org/10.1007/s10509-012-1301-5
- H. Saadat and B. Pourhassan, “FRW Bulk Viscous Cosmology with Modified Chaplygin Gas in Flat Space,” Astrophysics and Space Science, Vol. 343, No. 2, 2013, pp. 783-786. http://dx.doi.org/10.1007/s10509-012-1268-2
- N. Mazumder, R. Biswas and S. Chakraborty, “FRW Cosmological Model with Modified Chaplygin Gas and Dynamical System,” International Journal of Theoretical Physics, Vol. 51, No. 9, pp. 2754-2758. http://dx.doi.org/10.1007/s10773-012-1150-6