Open Journal of Microphysics
Vol.3 No.1(2013), Article ID:28218,7 pages DOI:10.4236/ojm.2013.31001
Relativistic Schrödinger Wave Equation for Hydrogen Atom Using Factorization Method
Department of Physics, Faculty of sciences, University of Mazandaran, Babolsar, Iran
Email: m.pahlavani@umz.ac.ir, h.rahbar@umz.ac.ir, mohsenarmani@gmail.com, mailto:m.pahlavani@umz.ac.ir
Received December 15, 2012; revised January 17, 2013; accepted January 25, 2013
Keywords: Relativistic Schrödinger Wave Equation; Factorization Method; Ladder Operators; Supersymmetry; Spin
ABSTRACT
In this investigation a simple method developed by introducing spin to Schrödinger equation to study the relativistic hydrogen atom. By separating Schrödinger equation to radial and angular parts, we modify these parts to the associated Laguerre and Jacobi differential equations, respectively. Bound state Energy levels and wave functions of relativistic Schrödinger equation for Hydrogen atom have been obtained. Calculated results well matched to the results of Dirac’s relativistic theory. Finally the factorization method and supersymmetry approaches in quantum mechanics, give us some first order raising and lowering operators, which help us to obtain all quantum states and energy levels for different values of the quantum numbers n and m.
1. Introduction
Inserting spin to Schrödinger equation as a relativistic correction, in the base of Pauli exclusion principle with two spinors is a context of perturbation theories [1]. Several other relativistic wave equations dealing with various aspects of spin have been put forth to address large variety of problems. Klein-Gordon equation for spin-(0) particles [2,3], wave equations for describing relativistic dynamics of a system of two interacting spin-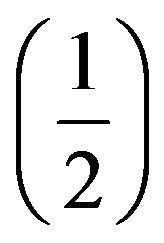 particles [4-6], Breit equation for two electrons [7] also called two body Dirac equation, generalized Bruit equation for two fermions [8], Duffin-Kemmer-Petiau (DKP) theory [9-11], of scalar and vector field for describing interacttion of relativistic spin-(0) and spin-(1) bosons [12-20] are examples of this topic. Some authors include Poincare invariant theory of classical spinning particles [21], quantum mechanical embedding of spinning particles and spin dependent gauge transformation between classical and quantum mechanics. All these theories fall under the class of perturbation theories and no account for inserting spin into the dynamics of motion. The paper organized as follow: We introduce the relativistic Schrö- dinger equation in Section 2. Then, in Section 3, we use mathematical aspect and obtain the exact solution for this wave equation. This approach improved using the so called supersymmetric quantum mechanics in framework of shape invariance in Section 4. Also we study given problem using the factorization method. These results lead us to have ladder operators which are represent the generators of respective algebra for relativistic particle.
particles [4-6], Breit equation for two electrons [7] also called two body Dirac equation, generalized Bruit equation for two fermions [8], Duffin-Kemmer-Petiau (DKP) theory [9-11], of scalar and vector field for describing interacttion of relativistic spin-(0) and spin-(1) bosons [12-20] are examples of this topic. Some authors include Poincare invariant theory of classical spinning particles [21], quantum mechanical embedding of spinning particles and spin dependent gauge transformation between classical and quantum mechanics. All these theories fall under the class of perturbation theories and no account for inserting spin into the dynamics of motion. The paper organized as follow: We introduce the relativistic Schrö- dinger equation in Section 2. Then, in Section 3, we use mathematical aspect and obtain the exact solution for this wave equation. This approach improved using the so called supersymmetric quantum mechanics in framework of shape invariance in Section 4. Also we study given problem using the factorization method. These results lead us to have ladder operators which are represent the generators of respective algebra for relativistic particle.
2. Relativistic Schrödinger Wave Equation
The general form of Schrödinger equation consist of angular momentum and spin can be define as [22],
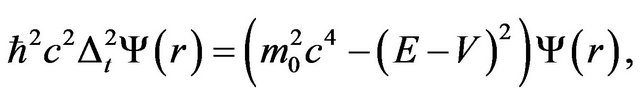 (1)
(1)
where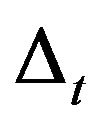 is given by,
is given by,
 (2)
(2)
where L is the orbital angular momentum operator and simply introduce as,
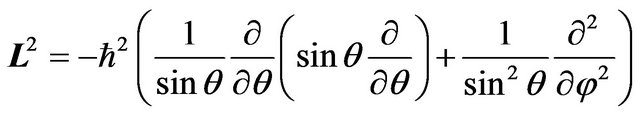 (3)
(3)
and S is the operator associated to the spin. The parameter 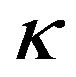 read as,
read as,
 (4)
(4)
Substituting Equation (2) in Equation (1) leads us to obtain following expression for Schrödinger equation,
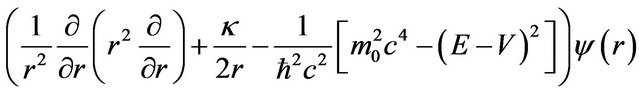
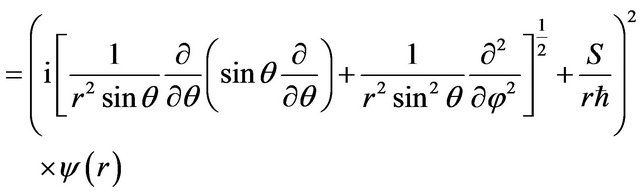
(5)
The radial and angular parts are separated by applying  in Equation (5). This substitution leads us to derive an equation which separated in totwo parts. One part related to coordinate r and other part depends on coordinate
in Equation (5). This substitution leads us to derive an equation which separated in totwo parts. One part related to coordinate r and other part depends on coordinate , so both parts had to equal a constant, say Γ. Thus Equation (5) gives us a radial differential equation,
, so both parts had to equal a constant, say Γ. Thus Equation (5) gives us a radial differential equation,
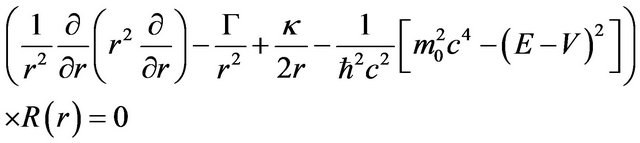
(6)
and an angular differential equation,
 (7)
(7)
In the following section we will attempt to obtain solutions of these equations for coulomb potential for spin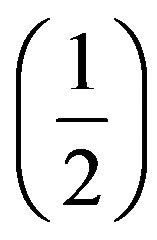 electrons as relativistic simple hydrogen atom.
electrons as relativistic simple hydrogen atom.
3. The Relativistic Hydrogen Atom
In order to solve the radial part of the Relativistic Schrödinger wave equation, we define new parameters as,
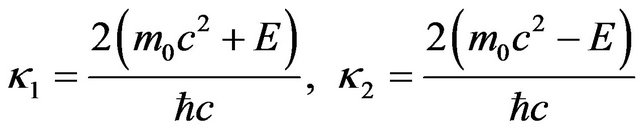 (8)
(8)
and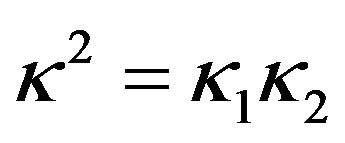 . Now we substitute Equation (8) in Equation (6), so the radial part of Schrödinger equation is rewritten as,
. Now we substitute Equation (8) in Equation (6), so the radial part of Schrödinger equation is rewritten as,
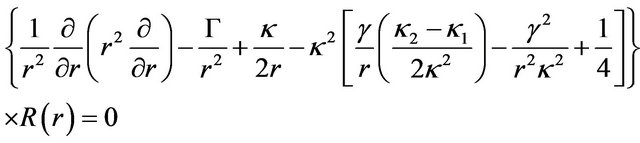
Where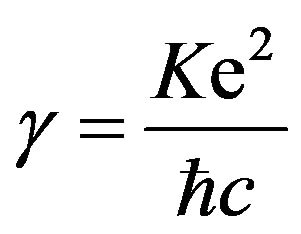 , K is an electrical constant and
, K is an electrical constant and 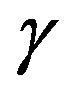 is a real constant which is identified by
is a real constant which is identified by 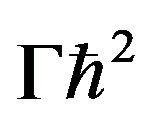 with eigenvalues
with eigenvalues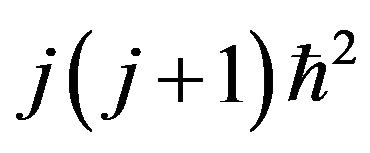 . Now, by introducing new variable,
. Now, by introducing new variable, 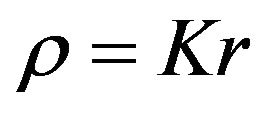 and substituting it in Equation (9) one obtain,
and substituting it in Equation (9) one obtain,
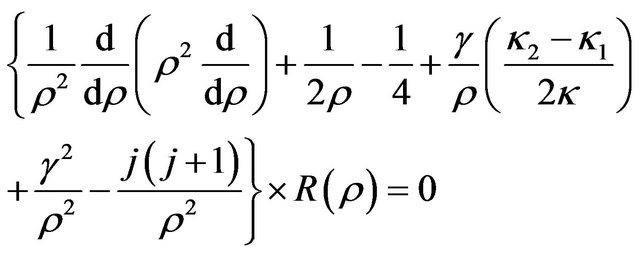
In order to obtain the exact solution for the equation (10), we need to consider the radial wave function 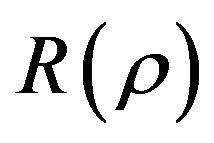 as,
as,
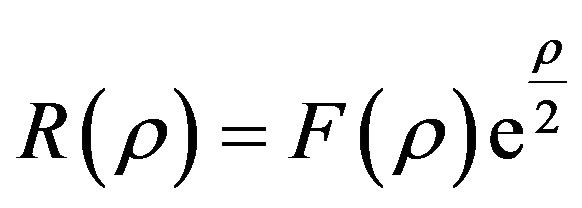 (11)
(11)
Here  is a polynomial of finite order in
is a polynomial of finite order in  after substituting of this definition in Equation (10), result the following second order differential equation for
after substituting of this definition in Equation (10), result the following second order differential equation for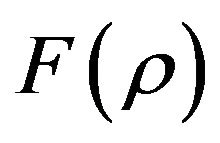 ,
,
 (12)
(12)
Where 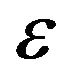 is,
is,
 (13)
(13)
Now we have to modify this equation with the associated Laguerre differential equation. For the real parameter  and
and  this differential equation in the interval
this differential equation in the interval 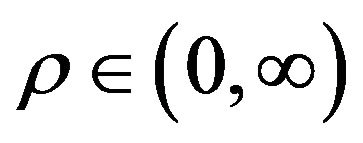 is defined as follows [23],
is defined as follows [23],
 (14)
(14)
where indices n and m are non-negative integers with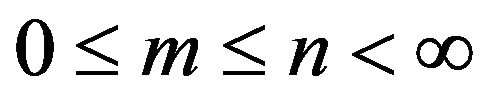 . So it is required to define function
. So it is required to define function 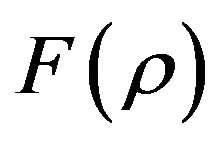 as,
as,
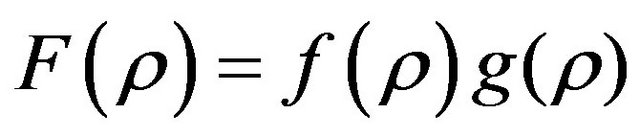 (15)
(15)
By substituting this definition in Equation (12) we have,
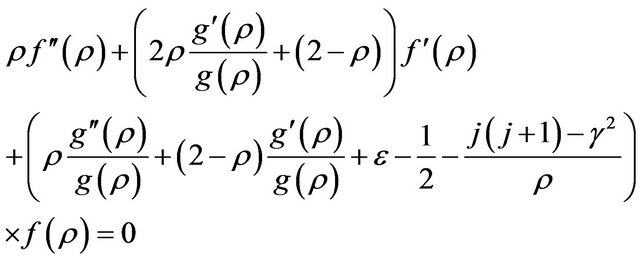 (16)
(16)
By modifying this equation with the associated Laguerre differential equation (14), in the first step we conclude the function 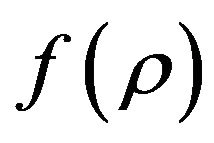 is corresponding to the associated Laguerre function
is corresponding to the associated Laguerre function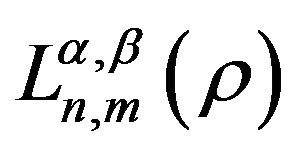 . The Rodrigues representation for associated Laguerre differential equation is given by,
. The Rodrigues representation for associated Laguerre differential equation is given by,
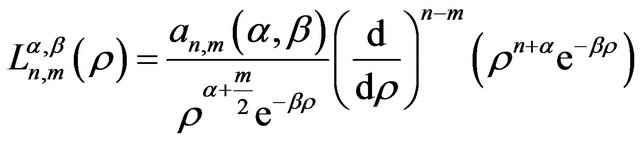 (17)
(17)
In which 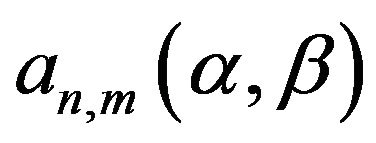 is the normalization coefficient and is also obtained by,
is the normalization coefficient and is also obtained by,
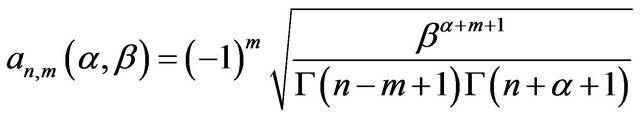 (18)
(18)
In addition to the Equation (17) for function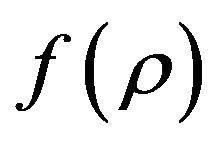 , this modification leads us to obtain the function
, this modification leads us to obtain the function 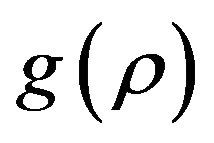 as,
as,
 (19)
(19)
Here C is the normalization coefficient and the parameter is evaluated by,
is evaluated by,
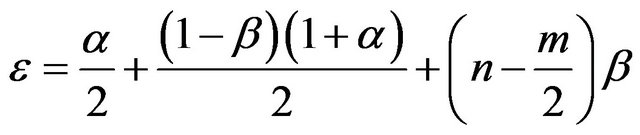 (20)
(20)
According to parameters 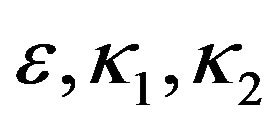 and
and , one can derive the energy levels
, one can derive the energy levels  in Equation (20) for bound states as,
in Equation (20) for bound states as,
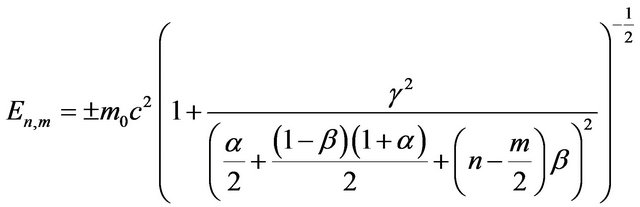
(21)
Finally the corresponding wave functions 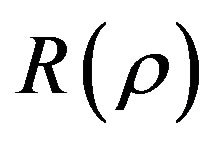 for these bound states, according to the Equations (11), (15) and (19) can be written as,
for these bound states, according to the Equations (11), (15) and (19) can be written as,
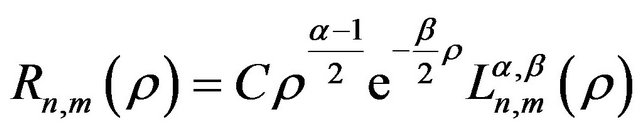 , (22)
, (22)
In order to represent an exact view of obtained results, the radial wave function  and values of energy spectrum
and values of energy spectrum 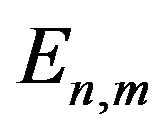 are showed in Table 1 for the different quantum numbers n and m.
are showed in Table 1 for the different quantum numbers n and m.
Also, in order to show the effect of spin on the energy spectrum, the obtained energy spectrum of radial part from solving relativistic Schrödinger equation are illustrated in Figure 1 and Figure 2 as function of quantum numbers n and m.
We may also derive the eigen function of the angular part of the relativistic Schrödinger equation similar to the solution of the radial part. The angular Equation (7) can be further separated by substituting,
 .
.
Table 1. Radial wave function and energy spectrum. Here n and m are the quantum numbers and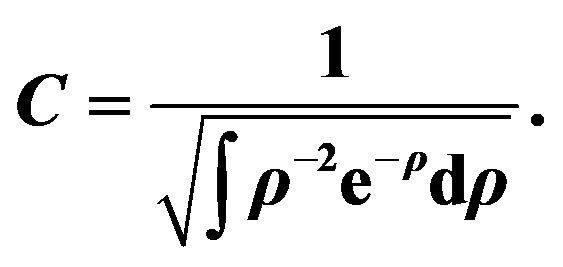 we assume
we assume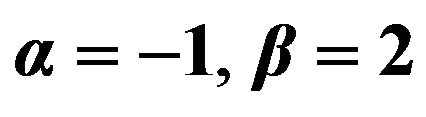 .
.
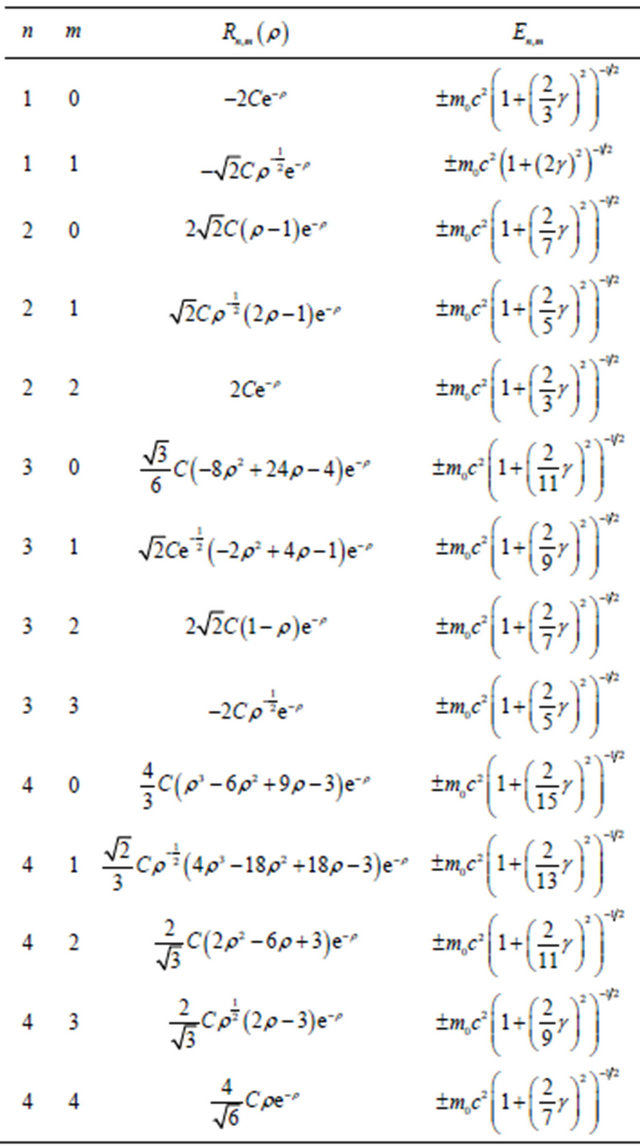
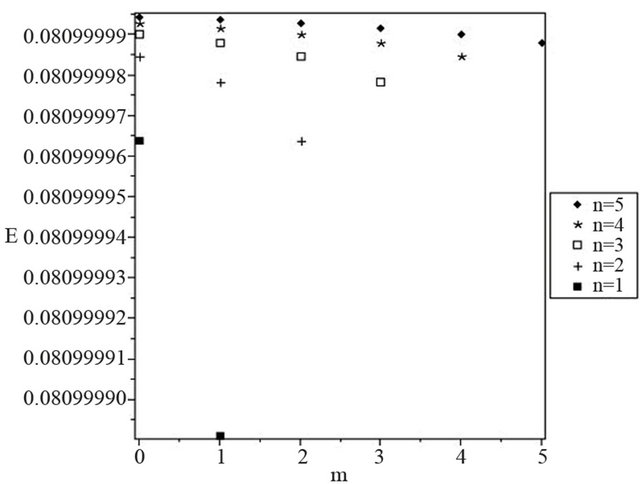
Figure 1. Energy spectrum for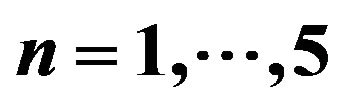 .
.
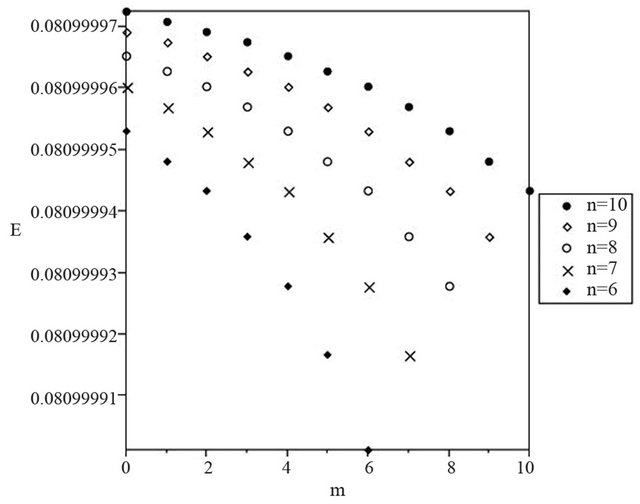
Figure 2. Energy spectrum for .
.
We take 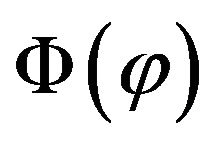 as follow,
as follow,
 (23)
(23)
So for azimuthal part we have,
 (24)
(24)
where 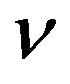 equal to square of quantum number m. The L·S term in Equation (24) point to the spin-orbit interacttion energy. This term simply consider as a perturbation to the final solution, so we ignore it. Here we define a new constant parameter,
equal to square of quantum number m. The L·S term in Equation (24) point to the spin-orbit interacttion energy. This term simply consider as a perturbation to the final solution, so we ignore it. Here we define a new constant parameter, 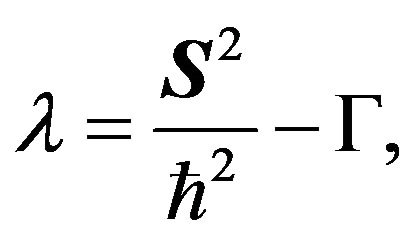 so the Equation
so the Equation
(24) is rewritten by following expression,
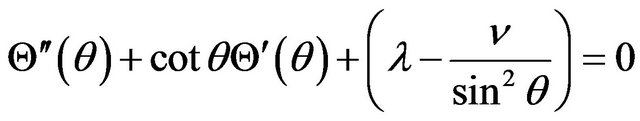 (25)
(25)
By introducing a new variable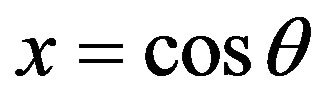 , one can rewrite Equation (25) as,
, one can rewrite Equation (25) as,
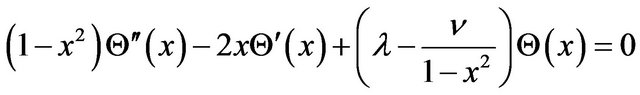 (26)
(26)
Now we consider wave function as,
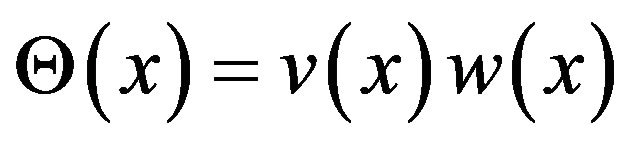 (27)
(27)
Thus the Equation (26) will become,
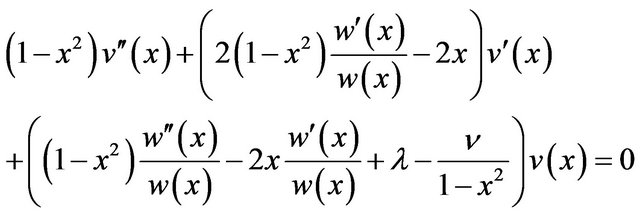 (28)
(28)
In order to obtain the wave function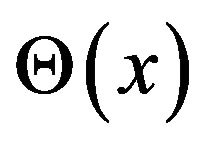 , we modify this equation with the associated Jacobi differential equation. Here for the real parameters
, we modify this equation with the associated Jacobi differential equation. Here for the real parameters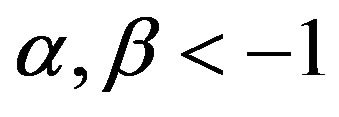 , this equation corresponding
, this equation corresponding 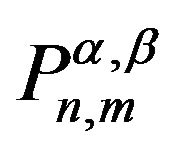 in the interval
in the interval 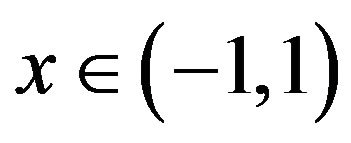 is introduced as [24],
is introduced as [24],
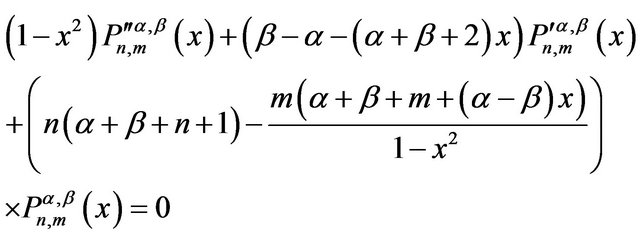 (29)
(29)
where, the indices n and m are non-negative integers with 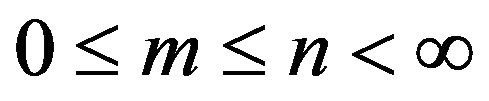 and for m = 0 Equation (29) converts to the differential equation corresponding to the Jacobi Polynomials.
and for m = 0 Equation (29) converts to the differential equation corresponding to the Jacobi Polynomials.
After the modification of Equations (28) and (29), in first step one can obtain  as,
as,
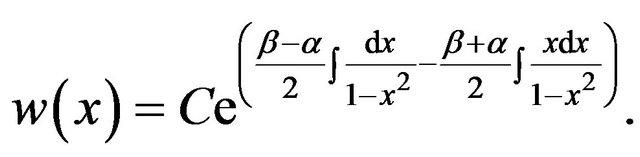 (30)
(30)
We conclude that the function  in Equation (27) is corresponding to the associated Jacobi function
in Equation (27) is corresponding to the associated Jacobi function 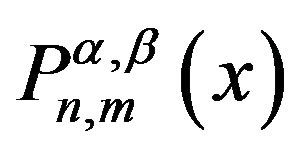 as solution of the Equation (29) which has the following Rodriguez representation,
as solution of the Equation (29) which has the following Rodriguez representation,
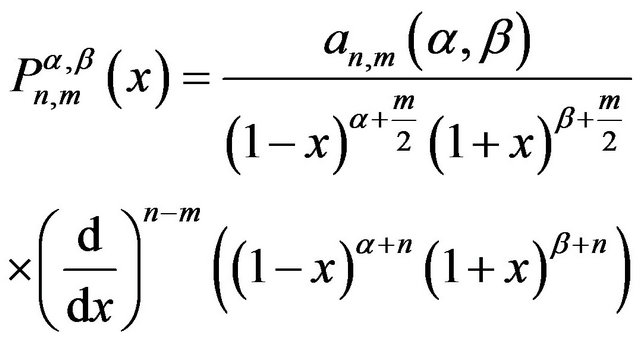 (31)
(31)
Here 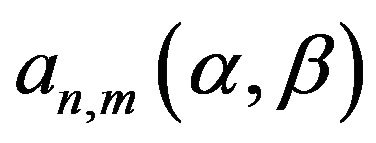 is the normalization coefficient which for
is the normalization coefficient which for 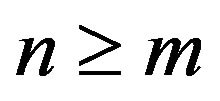 is given by,
is given by,
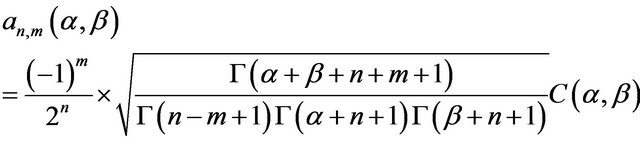 (32)
(32)
In which  is an arbitrary real constant independent of n and m. Therefore we have following relation for
is an arbitrary real constant independent of n and m. Therefore we have following relation for 
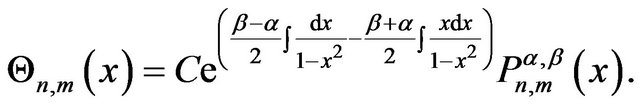 (33)
(33)
Finally, according to the Equations (23) and (29) the angular wave function is given by,
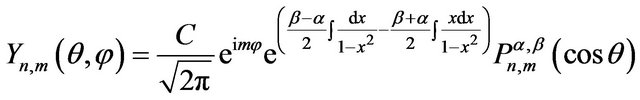
(34)
Parameter C is the normalization coefficient and easily evaluated using normalization condition.
4. Factorization Method to Wave Equations
In recent years supersymmetry and shape invariance in quantum mechanics have undergone a spectacular development. The concepts of shape invariance are developed in several branches of physics, such as atomi, nuclear and mathematical physics as well as quantum optics. Supersymmetry in quantum mechanics is based upon the factorization method in the framework of shape invariance. Factorization method goes back to Darboux, but was developed by Schrödinger in order to apply it to quantum mechanics [25,26]. There is a discussion of the factorization method in the review article of Infield and Hull [27], where they have been shown a large variety of the second-order differential equation with different boundary conditions set in six different types of factorizations. If a quantum mechanics problem admit context of supersymmetry, one able to factorize the Hamiltonian of quantum states in terms of a multiplication of the first-order differential operators as the shape invariance equation. In this approach, the Hamiltonians decomposed once in successive multiplication of lowering and raising operators, in such a way that the corresponding quantum states of successive levels are their Eigen states of them. These Hamiltonian are called partner and supersymmetric of each other.
In fact, three separate subject, i.e. the factorization method, the supersymmetry in the quantum mechanics and the shape invariance, nowadays converged at a point. The idea of supersymmetry in the context of quantum mechanics was first study by Nicolai and Witten and later by Cooper and Freedman et al. [28-30]. Recently, Gendenshtein put forward the concept of shape invariance in the context of the supersymmetric quantum mechanics [31]. As yet, according to the factorization method, many studies on the one-dimensional shape invariance potential in the framework of the supersymmetric quantum mechanics have been carried out [32-38]. One of the most well-known one-dimension quantum mechanical systems is the quantum harmonic oscillator [39]. There are other solvable systems with, say, a Morse potential, Scarf potential, Eckart potential, and many others [40-42]. These solvable potentials have established a tight connection with the pioneering work of Infield and Hull on factorization and algebraic solution of bound state problems. It should be noted that most of the solvable potentials are shape invariance. On this basis, the one dimension partner Hamiltonian is connected by supersymmetry transformations. The spectra of two partner Hamiltonians are identical, expect for the ground state. Supersymmetry played important role in analyzing of the quantum mechanical systems, since it can consider remarkable properties including degeneracy structure of the energy spectrum, the relations among the energy spectra of the various Hamiltonians, derivation of algebraic solutions and etc. In previous section, we determine the radial and angular wave functions of relativistic Hydrogen atom. In this section we apply the factorization method to radial and angular parts of Relativistic Schrödinger wave equation. In the first step, we consider the radial part of wave equation obtained in previous section. As mentioned in refs [43,44], one can factorize the associated Laguerre differential equation as the following shape invariance equations with respect to the parameters n and m,
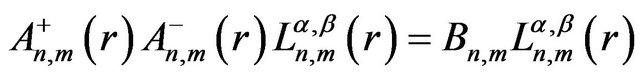
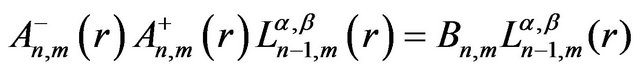 (35)
(35)
where
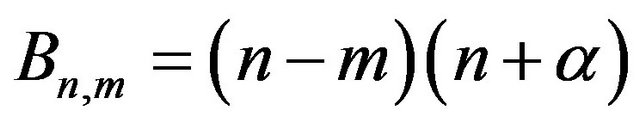 (36)
(36)
and its associated differential operators are,

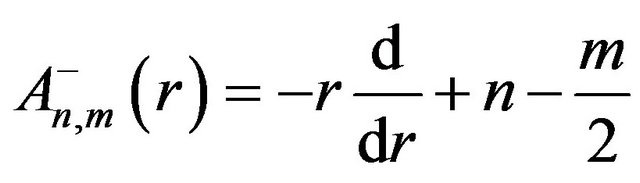 (37)
(37)
We note that the shape invariance Equations (35) can also be written as the lowering and raising relations,
 (38)
(38)
Therefore, we obtain the raising and lowering operators for the radial part of the relativistic Hydrogen atom. Next we apply factorization method to the angular part of the Relativistic Schrödinger wave equation. The shape invariance equations of the associated Jacobi differential equation respect to the parameters n and m given by [45,46],
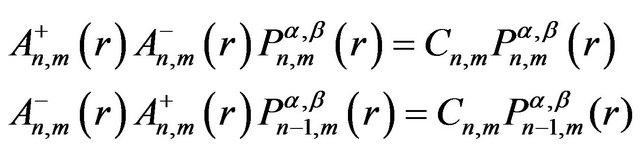 (39)
(39)
where
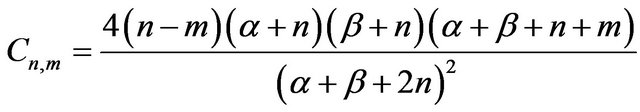 (40)
(40)
Therefore raising and lowering operators can be evaluated as,
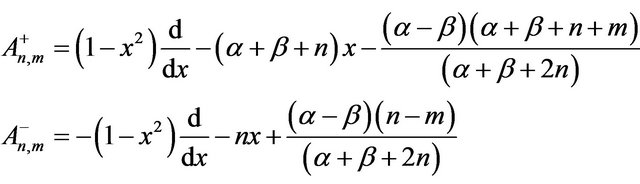 (41)
(41)
Also in the case of the shape invariance respect to m we have,
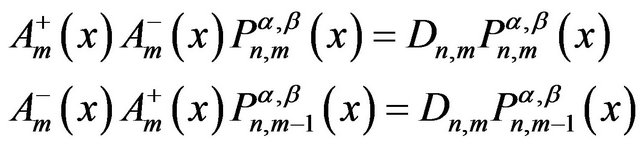 (42)
(42)
where
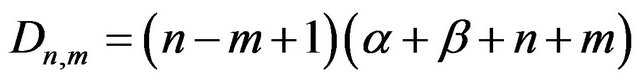 (43)
(43)
and,
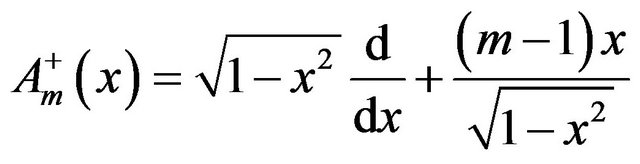
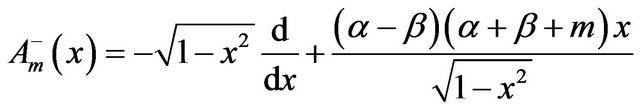 (44)
(44)
Note that the shape invariance Equations (39) contain the indices 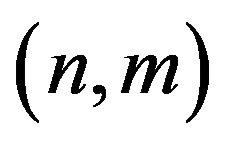 and also
and also 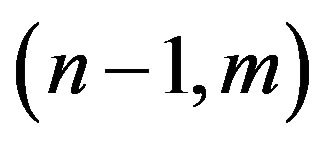 and the shape invariance Equations (42) contain
and the shape invariance Equations (42) contain and
and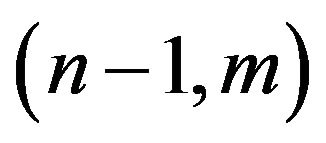 . The factorized Equations (39) together describe shape invariance with respect to n and also Equations (42) describe shape invariance with respect to m. One can easily rewrite shape invariance Equations (39) and (42) as the laddering relations with respect to the indices n and m respectively,
. The factorized Equations (39) together describe shape invariance with respect to n and also Equations (42) describe shape invariance with respect to m. One can easily rewrite shape invariance Equations (39) and (42) as the laddering relations with respect to the indices n and m respectively,
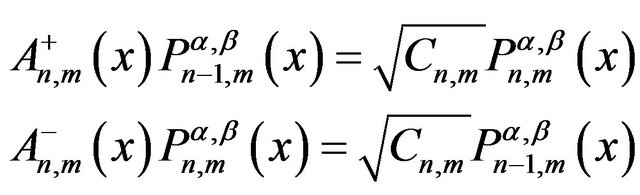 (45)
(45)
and,
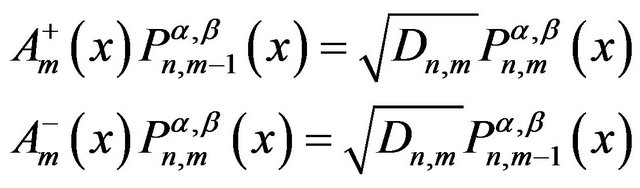 (46)
(46)
The general algebra covered this example completed by these raisingwors of radial part make  algebra and the raising andlowering operators of angular part make
algebra and the raising andlowering operators of angular part make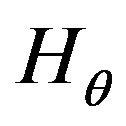 . Therefore we obtain following algebra,
. Therefore we obtain following algebra,
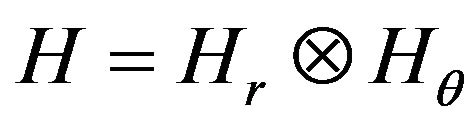 (47)
(47)
5. Conclusions
In this study, we successfully introduce spin in Schrö- dinger equation. The modification between reformed radial part of this equation for Hydrogen atom and the associated Laguerre differential equation, lead us to derive the exact bound states and corresponding radial wave functions.
Also by applying the factorization method we determine the lowering and raising operators which generate the shape invariance relation of Laguerre differential equation. In similar case, for angular wave functions of Hydrogen atom, the modification between reformed angular part of Schrödinger equation and the associated Jacobi differential equation, give us the exact angular wave functions. The resulting energy levels of Hydrogen atom in this theory are exactly match the results obtained using relativistic Dirac equation.
REFERENCES
- W. Greiner, “Quantum Mechanics,” 3rd Edition, SpringerVerlag, Berlin, 1994.
- I. T. Todorov, “Quasipotential Equation Corresponding to the Relativistic Eikonal Approximation,” Physical Review D, Vol. 3, 1971, pp. 2351-2356. doi:10.1103/PhysRevD.3.2351
- E. Brezin, C. Itzykson and J. Zinn-Justin, “Relativistic Balmer Formula Including Recoil Effects,” Physical Rview D, Vol. 1, No. 8, 1970, pp. 2349-2355. doi:10.1103/PhysRevD.1.2349.
- C. Itzykson and J. B. Zuber, “Quantum Field Theory,” McGraw-Hill, New York, 1985.
- E. Fermi and C. N. Yang, “A Relativistic Equation for Bound-State Problems,” Physical Review, Vol. 84, No. 6, 1951, pp. 1232-1242. doi:10.1103/PhysRev.84.1232
- E. E. Salpeter and H. A. Bethe, “Are Mesons Elementary Particles?” Physical Review, Vol. 76, No. 12, 1949, pp. 1739-1743. doi:10.1103/PhysRev.76.1739
- G. Breit, “Dirac’s Equation and the Spin-Spin Interactions of Two Electrons,” Physical Review, Vol. 39, No. 4, 1932, pp. 616-624. doi:10.1103/PhysRev.39.616
- G. D. Tsibidis, “Quark-Antiquark Bound States and the Breit Equation,” Acta Physica Polonica B, Vol. 35, No. 10, 2004, pp. 2329-2365.
- R. J. Duffin, “On the Characteristic Matrices of Covariant Systems,” Physical Review, Vol. 54, No. 12, 1939, p. 1114. doi:10.1103/PhysRev.54.1114
- J. T. Lunardi, L. A. Manzoni and B. M. Pimentel, “Duffin-Kemmer-Petiau Theory in the Causal Approa,” International Journal of Modern Physics A, Vol. 17, No. 2, 2002, p. 205. doi:10.1142/S0217751X02005682
- I. Boztosun, M. Karakus, F. Yasuk and A. Durmus, “Asymptotic Iteration Method Solutions to the Relativistic Duffin-Kemmer-Petiau Equation,” Journal of Mathematical Physics, Vol. 47, No. 6, 2006, Article ID: 062301. doi:10.1063/1.2203429
- Y. Nedjadi and R. C. Barrett, “The Duffin-Kemmer-Petiau Oscillator,” Journal of Physics A: Mathematical and General, Vol. 27, No. 12, 1994, p. 4301. doi:10.1088/0305-4470/27/12/033
- Y. Nedjadi and R. C. Barrett, “Solution of the Central Field Problem for a Duffin-Kemmer-Petiau Vector Boson,” Journal of Mathematical Physics, Vol. 35, No. 9, 1994, pp. 4517-4533. doi:10.1063/1.530801
- Y. Nedjadi and R. C. Barrett, “On the Properties of the Duffin-Kemmer-Petiau Equation,” Journal of Physics G: Nuclear and Particle Physics, Vol. 19, No. 1, 1993, pp. 87-98. doi:10.1088/0954-3899/19/1/006
- B. Boutabia-Cheraitia and T. Boudjedaa, “Solution of DKP Equation in Woods-Saxon Potential,” Physics Letters A, Vol. 338, No. 2, 2005, pp. 97-107. doi:10.1016/j.physleta.2005.02.029
- V. Y. Fainberg and B. M. Pimentel, “Duffin-KemmerPetiau and Klein-Gordon-Fock Equations for Electromagnetic, Yang-Mills and External Gravitational Field Interactions: Proof of Equivalence,” Physics Letters A, Vol. 271, No. 1-2, 2000, pp. 16-25. doi:10.1016/S0375-9601(00)00330-3
- J. T. Lunardi, P. M. Pimental and R. G. Teixeiri, “Remarks on Duffin-Kemmer-Petiau Theory and Gauge Invariance,” Physics Letters A, Vol. 268, No. 10, 2000, pp. 165-173. doi:10.1016/S0375-9601(00)00163-8
- L. Chetouani, M. Merad and T. Boudjedaa, “Solution of Duffin-Kemmer-Petiau Equation for the Step Potential,” International Journal of Theoretical Physics, Vol. 43, No. 4, 2004, pp. 1147-1159. doi:10.1023/B:IJTP.0000048606.29712.13
- A. Boumali, “Particule de Spin 0 dans un Potentiel d’Aharonov-Bohm,” Canadian Journal of Physics, Vol. 82, No. 1, 2004, pp. 67-74. doi:10.1139/p03-112
- D. A. Kulikov, R. S. Tutik and A. P. Yaroshenko “An Alternative Model for the Duffin-Kemmer-Petiau Oscillator,” Modern Physics Letters A, Vol. 20, No. 1, 2005, pp. 43-49. doi:10.1142/S0217732305016324
- N. Ogawa, “Quantum Mechanical Embedding of Spinning Particle and Induced Spin-Connection,” Modern Physics Letters A, Vol. 12, No. 21, 1997, pp. 1583-1588. doi:10.1142/S0217732397001618
- H. Koura and M. Yamada, “Single-Particle Potentials for Spherical Nuclei,” Nuclear Physics A, Vol. 671, No. 1-4, 2000, pp. 96-118. doi:10.1016/S0375-9474(99)00428-5
- J. Sadeghi “Superalgebras for Three Interacting Particles in an External Magnetic Field,” European Physical Journal B, Vol. 50, No. 3, 2006, pp. 453-457. doi:10.1140/epjb/e2006-00150-9
- A. F. Nikiforov and V. B. Uvarov, “Special Functions of Mathematical Physics,” Birkhauser, Basle, 1988.
- E. Schrödinger, “A Method of Determining Quantum-Mechanical Eigenvalues and Eigenfunctions,” Proceedings of the Royal Irish Academy, Vol. 46A, 1940, pp. 9-16.
- E. Schrödinger, “The Factorization of the Hypergeometric Equation,” Proceedings of the Royal Irish Academy, Vol. 47A, 1941, pp. 53-54.
- L. Infeld and T. D. Hull, “The Factorization Method,” Reviews of Modern Physics, Vol. 23, No.1, 1951, pp. 21-68. doi:10.1103/RevModPhys.23.21.
- H. Nicolai, “Supersymmetry and Spin Systems,” Journal of Physics A, Vol. 9, No. 9, 1976, p. 1497. doi:10.1088/0305-4470/9/9/010
- E. Witten, “Gauge Theories, Vertex Models, and Quantum Groups,” Nuclear Physics B, Vol. 380, No. 2-3, 1990, pp. 285-346.
- F. Cooper and B. Freedman, “Aspects of Supersymmetric Quantum Mechanics,” Annals of Physics, Vol. 146, No. 2, 1983, pp. 262-288. doi:10.1016/0003-4916(83)90034-9
- L. E. Gendenshtein, “Derivation of Exact Spectra of the Schrödinger Equation by Means of Supper Symmetry,” Letters to Jounal of Experimental and Theoretical Physics, Vol. 38, 1983, pp. 356-359.
- C. X. Chuan, “Exactly solvable potentials and the concept of shape invariance,” Journal of Physics A, Vol. 24, No. 19, 2006, p. L1165. doi:10.1088/0305-4470/24/19/008
- F. Cooper, A. Khare and U. Sukhatme, “Supersymmetry and Quantum Mechanics,” Physics Reports, Vol. 251, No. 5-6, 1995, pp. 267-385. doi:10.1016/0370-1573(94)00080-M
- A. Balantekin, “Algebraic Approach to Shape Invariance,” Physical Review A, Vol. 57, No. 6, 1998, pp. 4188- 4191. doi:10.1103/PhysRevA.57.4188
- A. Balantekin, M. A. C. Ribeiro and A. N. F. Aleixo, “Algebraic Nature of Shape-Invariant and Self-Similar Potentials,” Journal of Physics A: Mathematical and General, Vol. 32, No. 15, 1999, pp. 2785-2790. doi:10.1088/0305-4470/32/15/007
- J. F. Carinena and A. Ramos, “The Partnership of Potentials in Quantum Mechanics and Shape Invariance,” Modern Physics Letters A, Vol. 15, No. 16, 2000, p. 1079. doi:10.1142/S0217732300001249
- H. Aoyama, M. Sato and T. Tanaka, “N-Fold Supersymmetry in Quantum Mechanics: General Formalism,” Nuclear Physics B, Vol. 619, No. 1-3, 2001, pp. 105-127. doi:10.1016/S0550-3213(01)00516-8
- S. W. Qian, B. W. Huang and Z. Y. Gu, “Supersymmetry and Shape Invariance of the Effective Screened Potential,” New Journal of Physics, Vol. 4, 2002, pp. 13.1-13.6. doi:10.1088/1367-2630/4/1/313
- L. Landau and E. M. Lifshitz, “Quantum Mechanics,” Pergmon, Oxford, 1979.
- M. Morse, “Diatomic Molecules According to the Wave Mechanics. Ⅱ. Vibrational Levels,” Physical Review, Vol. 34, No. 1, 1929, pp. 57-64. doi:10.1103/PhysRev.34.57
- C. Eckart, “The Penetration of a Potential Barrier by Electrons,”Physical Review, Vol. 35, No. 11, 1930, pp. 1303- 1309. doi:10.1103/PhysRev.35.1303
- V. Bargmann, “On the Connection between Phase Shifts and Scattering Potential,” Reviews of Modern Physics, Vol. 21, No. 3, 1949, pp. 488-493. doi:10.1103/RevModPhys.21.488
- J. Sadeghi, “Factorization Method and Solution of the Non-Central Modified Kreutzer Potential,” Acta Physica Polonica A, Vol. 112, No. 1, 2007, pp. 23-28.
- M. A. Jafarizadeh and H. Fakhri, “The Embedding of Parasupersymmetry and Dynamical Symmetry intoGL(2, c) Group,” Annals of Physics, Vol. 266, No. 1, 1998, pp. 178- 206. doi:10.1006/aphy.1998.5788
- M. A. Jafarizadeh and H. Fakhri, “Supersymmetry and Shape Invariance in Differential Equations of Mathematical Physic,” Physics Letters A, Vol. 230, No. 3-4, 1997, pp. 164-170. doi:10.1016/S0375-9601(97)00161-8
- H. Fakhri and J. Sadeghi, “Supersymmetry Approaches to the Bound States of the Generalized Woods-Saxon Potential,” Modern Physics Letters A, Vol. 19, No. 8, 2004, p. 615. doi:10.1142/S0217732304013313

