Open Journal of Microphysics
Vol.2 No.4(2012), Article ID:24810,4 pages DOI:10.4236/ojm.2012.24007
Looking at Graviton Properties, as Either Classical or QM, in Nature, via Alicki-Van Ryn Experimental Realization
Chongqing University Department of Physics, Chongqing, China
Email: abeckwith@uh.edu
Received July 18, 2012; revised August 19, 2012; accepted September 2, 2012
Keywords: Planck’s Constant; Octonionic Geometry; Quantum Mechanics; Alicki-Van Ryn Test
ABSTRACT
Recently, the author read the Alicki-Van Ryn test as to behavior of photons in a test of violations of classicality. The same thing is proposed via use of a spin two graviton, using typical spin 2 matrices. While the technology currently does not exist to perform such an analysis yet, the same sort of thought experiment is proposed in a way to allow for a first principle test of the either classical or quantum foundations of gravity. The reason for the present manuscript topic is due to a specific argument presented in a prior document as to how 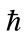 is formed from semiclassical reasoning. We referred to a procedure as to how to use Maxwell’s equations involving a closed boundary regime, in the boundary regime between Octonionic Geometry and quantum flat space. Conceivably, a similar argument could be made forgravitons, pending further investigations. Also the anlysis of if gravitons are constructed by a similar semiclassical argument is pending if gravitons as by the Alicki-Van Ryn test result in semiclassical
is formed from semiclassical reasoning. We referred to a procedure as to how to use Maxwell’s equations involving a closed boundary regime, in the boundary regime between Octonionic Geometry and quantum flat space. Conceivably, a similar argument could be made forgravitons, pending further investigations. Also the anlysis of if gravitons are constructed by a similar semiclassical argument is pending if gravitons as by the Alicki-Van Ryn test result in semiclassical 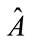 and
and  matrix observable eigenvalue behavior. This paper also indirectly raises the question of if Baysian statistics would be the optimal way to differentiate between
matrix observable eigenvalue behavior. This paper also indirectly raises the question of if Baysian statistics would be the optimal way to differentiate between  and
and 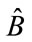 matrix observable eigenvalue behavior for reasons brought up in the conclusion.
matrix observable eigenvalue behavior for reasons brought up in the conclusion.
1. Introduction
What we are looking at is a way to analyze if the process of measuring gravitons/GW can be linked to either classical or quantum operations. The way to do it, is to look at a spin two version of the Alicki-Van Ryn test, a test which was reported for photons, and which we will now refer to via experimental protocols for measuring spin 2 gravitons [1,2]. The operators formed below, called A and B, are from an experiment initially done with photons, of spin 1/2. Matrices corresponding to spin 2, are detailed as to what to put in, the new version of these operators. Should the operators 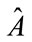 and
and 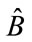 as given below for spin 2 particles obey quantum properties as detailed below by the Alicki-Van Ryn test, it is likely that the gravitons are quantum. If the operators have classical behavior, the matrices for
as given below for spin 2 particles obey quantum properties as detailed below by the Alicki-Van Ryn test, it is likely that the gravitons are quantum. If the operators have classical behavior, the matrices for 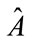 and
and 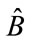 will have eignvalue behavior corresponding to classical behavior of gravitons. We leave the numerical work needed to get that determination to both computer modelers who know the experimental devices for making spin 2 measurements possible, and also the innovative scientists who would be needed to get a spin two version of the experiment done with spin 1/2 photons [1].
will have eignvalue behavior corresponding to classical behavior of gravitons. We leave the numerical work needed to get that determination to both computer modelers who know the experimental devices for making spin 2 measurements possible, and also the innovative scientists who would be needed to get a spin two version of the experiment done with spin 1/2 photons [1].
2. Looking at the Way to Form Spin Two 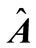 and
and 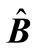 Operators Satisfying the Inequalities Given in Reference [1] via Representation of Spin 2 Matrices in Reference [2]
Operators Satisfying the Inequalities Given in Reference [1] via Representation of Spin 2 Matrices in Reference [2]
The starting point to this analysis, is to look at [1] where there is the following description of any two pairs of observables, 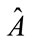 and
and 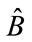 satisfying the condition as given in [1] that
satisfying the condition as given in [1] that
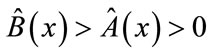 (1)
(1)
For all states of the system, defined by a hidden variable x, for which for classicality leads to the following always being true
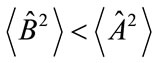 (2)
(2)
For QM, one has the reverse inequality in (2), namely [1]
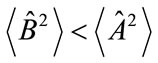 (3)
(3)
So happens that (3) above is equivalent to the minimum eigenvalue of [1]
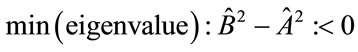 (4)
(4)
Whereas (4) is also equivalent to setting the minimum eigenvalue of [1]
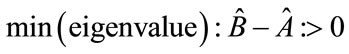 (5)
(5)
3. Forming Conditions to Test for (1) to (5) with Spin Two Gravitons, Experimentally
The idea is to look at what is given in [2] as far as a spin two particle and to construct operators 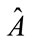 and
and 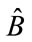 as matrix observables so as to come up with experimental tests. What we will be looking at a beam splitter version of the way to form observables
as matrix observables so as to come up with experimental tests. What we will be looking at a beam splitter version of the way to form observables 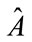 and
and  as given so as to determine for spin two objects if there is a classical or a quantum process occurring. Following [1] we use, simply
as given so as to determine for spin two objects if there is a classical or a quantum process occurring. Following [1] we use, simply
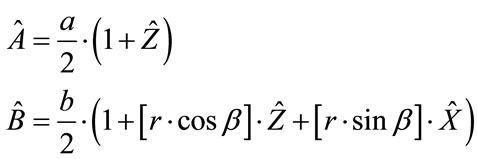 (6)
(6)
This means that the 1 is actually a 5 by 5 identity matrix.
The  and
and 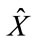 are matrices which are given in [2] as follows, namely
are matrices which are given in [2] as follows, namely
 (7)
(7)
 (8)
(8)
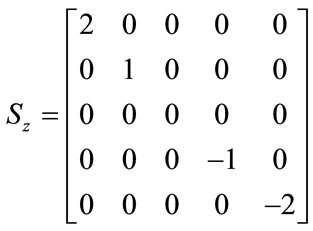 (9)
(9)
 (10)
(10)
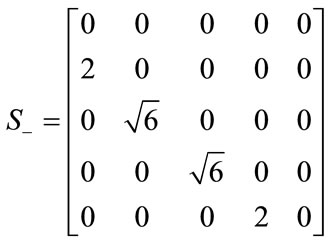 (11)
(11)
If one used 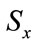 for
for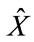 , and
, and 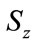 for
for  and 5 by 5 identity matrices in which then
and 5 by 5 identity matrices in which then 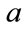 and then also
and then also 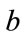 are both > 0 and with
are both > 0 and with 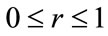 We can then look for the minimum Eigenvalues of
We can then look for the minimum Eigenvalues of  which should be greater for a spin 2 particle, if one wants to have quantum values assigned to a graviton.
which should be greater for a spin 2 particle, if one wants to have quantum values assigned to a graviton.
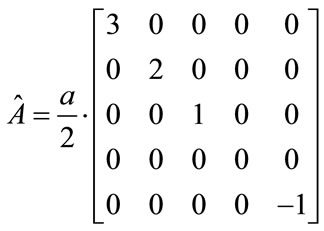 (12)
(12)
 (13)
(13)
We now are looking at the (13) – (12) Equation result which will be parlayed as
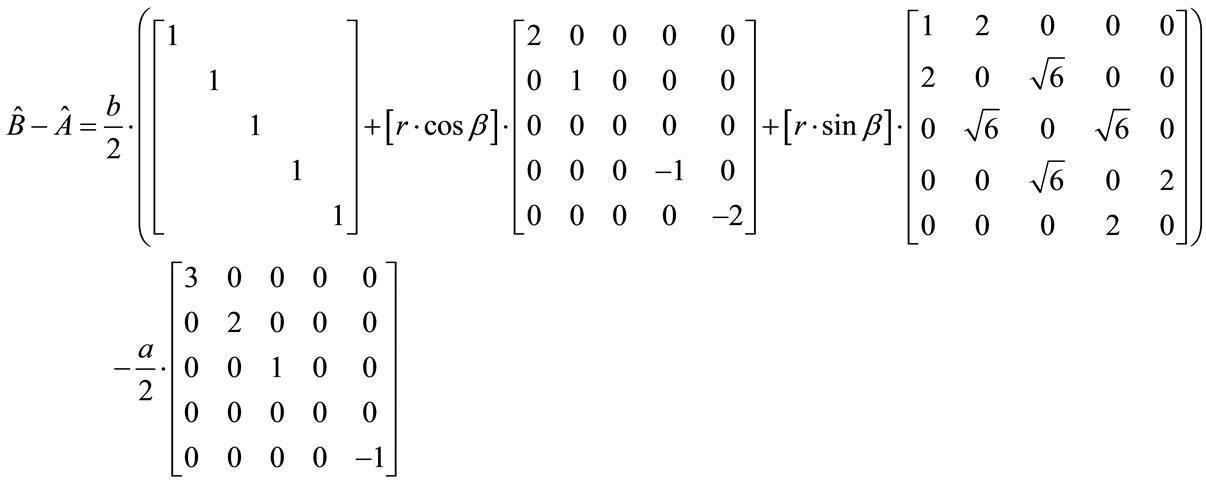 (14)
(14)
We need to find ratio relations between the different input parameters of (14) above so as to be able to find out if the minimum Eigenvalue of (14) is greater than zero, for a quantum results, or is less than zero for certain configurations for semi classical characteristics of a graviton.
This will have to be numerically simulated. In any case, note that in the case of spin 1/2 that [1] has a very simple interpretation, namely for a quantum behavior of spin 1/2 for there to be a minimum Eigenvalue of 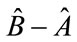 > 0 we need to have
> 0 we need to have
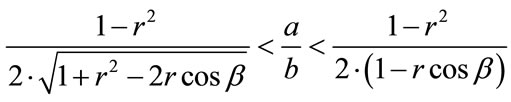 (15)
(15)
This, (15) is for a spin 1/2 particle. To be continued later will be a proof that if the minimum eignvalue for (14) is less than zero, that the graviton will be massive, which will be presented in a future publication.
4. Why Having a Semi Classical Intepretation of a Graviton Is Not Impossible
In a prior publication, Beckwith identified processes in which Planck’s constant could be founded in a pre quantum era. We will for the sake of completeness review these results. The first is to consider [3,4].
So if a Domain Wall Enters the Picture, Then What Does This Do to Structure Formation and Also Plank’s constant?
In [3,4] we are struck with how a semiclassical argument can be used to construct Table 1. In particular, we look at how Planck’s constant is derived, as in the electroweak regime of space time, namely that given the prime in both (16) and (17) is for a total derivative [5,6]
 (16)
(16)
Similarly [3-6]
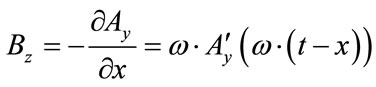 (17)
(17)
The A field so given would be part of the Maxwell’s equations given by [5] as, when  represents a Maxwell equation style operator, that in a vacuum, one would have for an A field [5,6]
represents a Maxwell equation style operator, that in a vacuum, one would have for an A field [5,6]
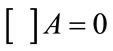 (18)
(18)
And for a scalar field 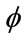
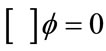 (19)
(19)
Following this line of thought we then would have an energy density given by, if 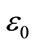 is the early universe permeability [6]
is the early universe permeability [6]
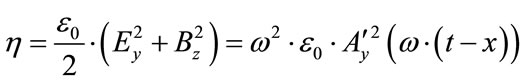 (20)
(20)
We integrate (20) over a specified E & M boundary, so that, then we can write the following condition namely

Table 1. Time interval dynamical QM/WD wapply? Consequences.
[5,6].
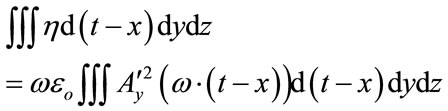 (21)
(21)
(21) would be integrated over the boundary regime from the transition from the Octonionic regime of space time, to the non Octonionic regime, assuming an abrupt transition occurs, and we can write, the volume integral as representing [5,6]
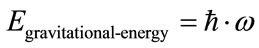 (22)
(22)
Our contention for the rest of this paper, is that Mach’s principle will be necessary as an information storage container so as to keep the following, i.e. having no variation in the Planck’s parameter after its formation from electrodynamics considerations as in (21) and (22). Then by applying [5,6]
 (23)
(23)
What we are arguing is that if there is a way to identify Planck’s constant as having a semi classical genesis, then the same will be true with gravitons. And that perhaps a semiclassical genesis for gravitons may occur at the same time as for the formation of Planck’s constant. This is to be determined experimentally.
5. Conclusions. We Need to Reconsider the Role of Quantum Gravity Models at the on Set of Inflation
We are stuck with the necessity in all Quantum gravity models as of putting in an initial time step ‘by hand’ so to speak which raises fundamental issues of what would form an initial time step in Quantum gravity. The other way to look at the role of an undefined initial starting point for time, which we put in by ‘hand’ is that the special nature of time itself may be if experimentally verified, via observations, the best hope we have of falsifiable measurements of G.t’ Hooft’s conjecture [7,8] that QM is embedded within a classical physics frame work which we have yet to fully develop.
Perhaps lead to signals from early universe GW which may confirm or falsify the role of QM in initial universe conditions. As well as the role that set as a working approximation [3,4].
 (24)
(24)
affects the formation of baryonic matter fluctuations (24) may play a role in the formation of Table 1 above.
Finally, if a similar set of circumstances to obtaining semi classical Planck’s constant arises from an observed semi classical treatment of gravitons arises due to imposing [2] upon the matrices of [1], a different statistical treatment of data than what is done in [1] will have to be used than the typical Baysian statistics used typically in experiment. A good case can be made, and will be in a subsequent article that what is called frequentist analysis [9] will have to be implemented, due to the scarcity of signal data which will be realistically extremely hard to obtain, for gravitons. The trouble spot is known as [9] “Maximum likelihood” and configuring an optimum set of parameters for (1) to (5) will affect a spin 2 replacement for (15) above which is for spin 1/2.
6. Acknowledgements
This work is supported in part by National Nature Science Foundation of China grant No110752
REFERENCES
- G. Brida, et al., “Improved Implementation of the AlickiVan Ryn Nonclassicality Test for a Single Particle Using SI Detectors,” Physical Review A, Vol. 79, No. 4, 2009. http://www.nist.gov/customcf/get_pdf.cfm?pub_id=900940
- “Spin Operators and Matrices,” 2012. http://www.easyspin.org/documentation/spinoperators.html
- A. Beckwith, “Is Quantum Mechanics Involved at the Start of Cosmological Evolution? Does a Machian Relationship between Gravitons and Gravitinos Answer This Question?” Hadronic Press, Palm Harbor, 2012. http://vixra.org/abs/1206.0023
- A. Beckwith, “Is There a Change in the Baryonic Structure Formation If Quark Strings and Domain Walls Exist at about the Electro-Weak Era?” 2012. http://vixra.org/abs/1207.0034
- U. Bruchholz, “Derivation of Planck’s Constant from Maxwell’s Electrodynamics,” Progress in Physics, Vol. 4, 2009, p. 67. http://www.ptep-online.com/index_files/2009/PP-19-07.PDF
- U. Bruzchholz, “Key Notes on a Geometric Theory of Fields,” Progress in Physics, Vol. 2, 2009, pp. 107-113.
- G.’t Hooft, “Determinism Beneath Quantum Mechanics,” 2002. http://arxiv.org/PS_cache/quant-ph/pdf/0212/0212095v1.pdf
- G.’t Hooft, “Quantum Mechanics and Determinism,” In: P. Frampton and J. Ng, Eds., Proceedings of the Eighth International Conference on Particles, Strings and Cosmology, Rinton Press, Princeton, 2001, pp. 275-285.
- L. Lyons, “Discovery or Fluke: Statistics in Particle Physics,” Physics Today, Vol. 65, No. 7, 2012, pp. 45-51.

