Open Journal of Geology
Vol.05 No.06(2015), Article ID:56956,7 pages
10.4236/ojg.2015.56034
Evaluation of Hydraulic Aperture of the Joints of Behesht Abad Dam Foundation, Iran
Ameneh F. Dardashti*, Rasoul Ajalloeian
Department of Geology, University of Isfahan, Isfahan, Iran
Email: *ameneh.dardashti@yahoo.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 15 May 2015; accepted 5 June 2015; published 8 June 2015
ABSTRACT
The fluid flow in rock fractures during shear processes has been an important issue in rock mechanics. During shearing, because of the stiffer rock matrix, most deformation occurs in the joints, in the form of normal and shear displacement. Since the joints are rough, deformations will also change the joint aperture and fluid flow. In this article, the hydraulic apertures of the joints of dolomitic limestone foundation of Behesht Abad dam are investigated. Firstly, geological data during a site investigation phase in dam site is gathered, and then related calculations are done and the hydraulic conductivity of the joints is evaluated. The results indicate that the hydraulic conductivity of the joints is reasonable.
Keywords:
Behesht Abad Dam, Hydraulic Aperture, Hydro-Mechanical Behavior, Seepage

1. Introduction
The fluid flow in a rock mass is usually governed by three factors: the fluid properties, the void geometry and the fluid pressure at the joint boundary. The void geometry, i.e. the geometry of the volume between the joint surfaces, is governed by the geological history and can be described by several geometrical parameters, as aperture, frequency distribution, spatial correlation and contact area. These geometrical parameters are related in various ways to the joint void geometry.
As a consequence of engineering works in rock mass, deformation of both the joints and intact rock will usually occur as a result of stress changes. Due to the stiffer rock matrix, most deformation occurs in the joints, in the form of normal and shear displacement [1] [2] . If the joints are rough, deformations will also change the joint aperture and fluid flow.
Traditionally, fluid flow through rock joints has been described by the cubic law, which follows the assumption that the joints consist of two smooth, parallel plates. Real rock joints, however, have rough walls and variable aperture, as well as asperity areas where the two opposing surfaces of the joint walls are in contact with each other. According to this, apertures can generally be defined as mechanical (geometrically measured such as with epoxy injection) or hydraulic (measured by analysis of the fluid flow).
The mechanical joint aperture (E) is defined as the average point-to-point distance between two rock joint surfaces (Figure 1), perpendicular to a selected plane. If the joint surfaces are assumed to be parallel in the x-y plane, then the aperture can be measured in the z direction. Often, a single, average value is used to define the aperture, but it is also possible to describe it stochastically. Usually, the mechanical aperture is determined from a two-dimensional (2-D) joint section, which is a part compound of the real 3-D surface.
The hydraulic aperture (e) can be determined both from laboratory fluid-flow experiments and borehole pump tests in the field. Fluid flow through rock joints is often represented as laminar flow between two parallel plates. The equivalent, smooth wall hydraulic aperture (e) can be obtained from flow tests using the modified form of Darcy’s law.
Fluid flow through a porous medium such as many soils and sedimentary rocks can be described by Darcy’s law (1-D flow):
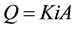 (1)
(1)
where Q is the volumetric flow per unit area A, normal to the flow. Q is thus related to the dimension less hydraulic gradient i, and to the hydraulic conductivity K. The latter is a material property of the fluid and geological medium and may be written as
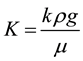 (2)
(2)
where k is the intrinsic permeability, g is the acceleration due to gravity (9.81 m/s2), µ is the dynamic viscosity of the fluid (1 × 10−3 Ns/m2 for pure water at 20˚C) and ρ is the fluid density (998 Kg/m3 for pure water at 20˚C).
For fluid flow through rock joints, it is common to consider the joint as composed of two smooth parallel plates and the flow to be steady, single phase, laminar and incompressible. Under these conditions, the hydraulic joint conductivity (Kj) may be written:
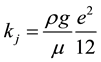 (3)
(3)
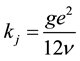 (4)
(4)
where ν is the kinematic viscosity of the fluid (1 × 10−6 m2/s for pure water at 20˚C) and e is the hydraulic aperture. The hydraulic joint conductivity is a parameter expressing the flow through the joint under the influence of frictional losses, tortuosity and channeling. These factors depend on the geometry of the flow channels and the fluid viscosity.
Assuming that Darcy’s law can also be applied to flow in rock joints, setting A = ew, we obtain
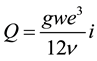 (5)
(5)
Figure 1. Definition of mechanical joint aperture (E).
where i is the dimensionless hydraulic gradient and w is the breadth of the flowing zone between the parallel plates. This equation is usually called the “cubic law”. One must keep in mind that Equation (5) is derived for an “open” channel, i.e. the planar surfaces remain parallel and are thus not in contact at any point [3] [4] , so joint permeability is completely dependent on joint aperture (because of the third power of joint hydraulic aperture in cubic law).
The aperture distribution of a joint is only valid at a certain state of rock stress and pore pressure. If the effective stress or the lateral position between the surfaces changes, as during shearing, the aperture distribution will also be changed. During shearing, because of the stiffer rock matrix, most deformation occurs in the joints, in the form of normal and shear displacement. Since the joints are rough, deformations will also change the joint aperture and fluid flow. By coupling the mechanical aperture changes to the hydraulic conductivity changes, a hydro-mechanical coupling is achieved.
An important distinction has to be made between the theoretical smooth wall hydraulic aperture (e) and the real mechanical aperture (E). As shown in (Figure 2), owing to the wall friction and the tortuosity, (E) is generally larger than (e) during normal loading and unloading, which means that a rough joint requires a larger aperture than a smooth joint for the same water conducting capacity [4] [5] .
When Darcy’s law is applied to natural rock joints with rough surfaces, many researchers suggests that a correction factor has to be used, which accounts for deviations from the ideal conditions assumed in the parallel smooth plate theory. A study by Zimmerman and Bodvarsson (1996) concluded that the hydraulic aperture was less than the mechanical aperture by a factor that depended on the ratio of the mean value of the aperture to its standard deviation. Results by Hakami (1995) showed that the ratio between mechanical mean aperture (E) and hydraulic aperture (e) was 1.1 - 1.7 for joints with a mean aperture of 100 - 500 µm [4] .
2. Methods and Calculations
On the basis of experimental data (Figure 2), Barton proposed the following exponential function, relating the
Figure 2. Comparison of real mechanical apertures (E) with theoretical smooth wall conducting apertures (e). The mismatch is caused by flow losses due to tortuosity and surface roughness [4] [5] .
hydraulic aperture (e) to the mechanical aperture (E) and JRC.
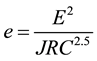 (6)
(6)
This empirical formula gives the hydraulic aperture (to be used in cubic law) as a function of the mechanical aperture and joint roughness coefficient JRC. The JRC coefficient describes the peak roughness of correlated, mated surfaces, and can be estimated either by correctly designed tilt, push or pull tests on jointed rock samples or by visual comparison of measured roughness profiles from the joint surface with a standard profiles [4] [5] .
One should note that this equation is only valid for E ≥ e. The background data mainly comes from normal deformation fluid flow tests. Just a few cases come from shear deformation fluid flow tests. There is a clear trend following an exponential function. The curves illustrated in (Figure 3), show the predicted relation between (E/e) and hydraulic aperture (e) for different values of JRC, according to Equation (6).
The latter shear-flow coupling tests have a consistent trend with Barton’s model prediction during the initial shear process. The shear testing results revealed that the change of hydraulic conductivity is approximately similar to that of the dilatancy of a joint. The hydraulic conductivity increases rapidly, by about 1.2 - 1.6 orders of magnitude for the first phase of shear displacement. After passing the residual shear stress, the hydraulic conductivity becomes gradually a constant value with increasing shear displacement. However, increasing deviation between measured and predicted hydraulic conductivity of rock joint samples has been observed with increasing shear displacement [6] -[8] . So the model was obviously slightly objective, and therefore only an approximate method. During shearing, this regular exponential behavior appears to break down. Under an increasing shear displacement the joint dilates and both the hydraulic and the mechanical aperture increase [9] [10] .
Until Olsson and Barton (2001) proposed an improved model on the basis of the performed hydro-me- chanical shear tests. It is an empirical engineering model and not a theoretical scientific model. As shear tests on rough rock joints are composed of at least two major parts, pre peak-peak and post-peak, depends on shear displacement. The model considers these two basic phases. In the first phase, where the joint wall roughness is not destroyed, the peak 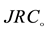 should be used in Equation and hydraulic aperture (e) can be calculated by Equation (7) up to 0.75 peak shear displacement (δS ≤ 0.75δsp)
should be used in Equation and hydraulic aperture (e) can be calculated by Equation (7) up to 0.75 peak shear displacement (δS ≤ 0.75δsp)
Figure 3. An empirical relation incorporating JRC and aperture which satisfies the trends exhibited by available flow data [4] .
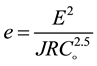 (7)
(7)
In the second phase, where the geometry of the joint walls is changing with increasing shear displacement, the JRCmob (mobilized value of JRC) should be used. Hydraulic aperture (e) can be calculated by Equation (8) for δs ≥ δsp (peak shear displacement)
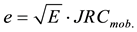 (8)
(8)
During this phase, gouge is being produced but as the joint is dilating, some of the gouge is probably flushed to the sides of developing flow channels. Based on normal loading/unloading, during increased normal stress, the hydraulic aperture (e) decreases, which causes an increase in E/e due to tortuosity. In shear behavior, during the first part of each plotted shear path in (Figure 4), the E/e ratio is first slightly decreasing and thereafter increasing.
This initial part in this figure belongs to the pre peak-peak shear displacement. When the asperities along the joint walls are not destroyed and the hydraulic aperture is probably decreasing due to shear-related closing of small voids. Thereafter the geometry of the joint walls is in a changing phase (breakdown) where the asperities get worn and damaged under the increasing shear deformation. The size of roughness decrease in JRCmob depends on the strength of the asperities, on the applied normal load and on the shear deformation. Furthermore new flow paths open and others close due to the increasing areas of contact between the joint walls and due to gouge production. The gouge production will probably decrease the hydraulic aperture. So, the increase in E/e during shearing depends not on the same phenomena as during normal loading and unloading [4] .
The intermediate phase, between phase one and two (δs = 0.75δsp ? δsp) is difficult to define with any model and it is recommended for the present that the two phases are connected with each other by a transition curve [4] .
During the following years, a number of shear-flow coupling tests were carried out on kinds of rock fractures to evaluate the effects of contact area, surface roughness and stress dependence on the behavior of fluid flow through rock fractures and more researches are necessary to make more quantitative assessments [11] [12] .
Figure 4. Curves relating the hydraulic aperture e and the ratio E/e for both normal and shear behavior [4] .
3. Case Study
Hydro-mechanical shear tests have shown widely used constitutive models that are very significant in rock mechanics and yields results that are most suitable for normal loading and unloading and for shear with limited damage or gouge production. So, for calculating conductivity changes of rock joints during shearing, one has first to assume the initial JRC value and the initial mechanical aperture. Thereafter, one has to calculate the changes of the mechanical aperture and JRCmob during shearing. These parameters should then be used in Equations (7)-(8) to calculate the changes of the hydraulic aperture during shearing. Therefore, it is possible to calculate the hydraulic conductivity (Kj) of each joint set.
For calculating the amounts of hydraulic aperture of the joints of Behesht Abad dam foundation, 5 direct shear tests done along the dolomitic limestone joints of foundation under different normal stresses, were selected.
In site investigation phase, the initial mechanical aperture of the joints of dam foundation, was measured 1 - 2 mm, so 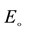 = 2 mm was selected and related calculations were done and the hydraulic conductivity of each joint set was evaluated. Joints which were found in field are studied to make sure that the joints are not just on the surface and their traces are seen on the check holes. The results of calculating the mechanical and hydraulic apertures and hydraulic conductivity of each joint set are summarized in (Table 1).
= 2 mm was selected and related calculations were done and the hydraulic conductivity of each joint set was evaluated. Joints which were found in field are studied to make sure that the joints are not just on the surface and their traces are seen on the check holes. The results of calculating the mechanical and hydraulic apertures and hydraulic conductivity of each joint set are summarized in (Table 1).
The results show that with increasing normal stress on the joints, the mechanical aperture of joints decreases. Consequently hydraulic aperture and finally hydraulic conductivity reduce too. Based on this, it's concluded that with increasing depth, the apertures decrease and as a result, hydraulic conductivity reduces. (Figure 5) illustrates the changes of joints mechanical aperture versus the changes of normal stress in shear tests along the joints of dam foundation.
4. Conclusions
A fully coupled mechanical-hydraulic analysis is considered, in which fracture conductivity is dependent on normal and shear displacement. In a rock mass because of the stiffer rock matrix, mechanical deformations will mainly occur as normal and shear deformations in the joints. This deformation will change the joint aperture and the hydraulic conductivity of the joints.
Table 1. The results of calculating the mechanical and hydraulic apertures and hydraulic conductivity of each joint set.
Figure 5. The changes of joint mechanical aperture versus the changes of normal stress in direct shear tests along the joints.
For calculating the conductivity changes of rock joints of Behesht Abad dam foundation during shearing, first the initial JRC and the initial mechanical aperture are measured. Thereafter, the changes of the mechanical aperture and JRCmob during shearing are calculated and related calculations are done. Then, the amounts of hydraulic aperture and hydraulic conductivity of the joints are evaluated and the results indicate that the hydraulic conductivity of the joints is reasonable.
Acknowledgements
This paper was supported by the department of geology of the University of Isfahan. The authors would like to thank the members.
References
- Goodman, R.E. (1989) Introduction to Rock Mechanics. 2nd Edition, John Wiley & Sons Ltd., New York.
- Bandis, S., Lumsden, A. and Barton, N. (1983) Fundamentals of Rock Joint Deformation. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 20, 249-268. http://dx.doi.org/10.1016/0148-9062(83)90595-8
- Priest, S.D. (1993) Discontinuity Analysis for Rock Engineering. Chapman & Hall, London.
- Olsson, R. and Barton, N. (2001) An Improved Model for Hydro-Mechanical Coupling during Shearing of Rock Joints. International Journal of Rock Mechanics & Mining Science, 38, 317-329. http://dx.doi.org/10.1016/S1365-1609(00)00079-4
- Barton, N., Bandis, S. and Bakhtar, K. (1985) Strength Deformation and Conductivity Coupling of Rock Joints. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 22, 121-140. http://dx.doi.org/10.1016/0148-9062(85)93227-9
- Ahola, M.P., Mohanty, S. and Makurat, A. (1996) Coupled Mechanical Shear and Hydraulic Flow Behavior of Natural Rock Joints. Developments in Geotechnical Engineering, 79, 393-423. http://dx.doi.org/10.1016/S0165-1250(96)80034-4
- Esaki, T., Du, S., Mitani, Y., Ikusada, K. and Jing, L. (1999) Development of a Shear-Flow Test Apparatus and Determination of Coupled Properties for a Single Rock Joint. International Journal of Rock Mechanics & Mining Science, 36, 641-650. http://dx.doi.org/10.1016/S0148-9062(99)00044-3
- Olsson, R. (1998) Mechanical and Hydro-Mechanical Behavior of Hard Rock Joints―A Laboratory Study. Ph.D. Thesis, Chalmers University of Technology, Gothenburg.
- Gentier, S., Lamontagne, E., Archambault, G. and Riss, J. (1997) Anisotropy of Flow in a Fracture Undergoing Shear and Its Relationship to the Direction of Shearing and Injection Pressure. International Journal of Rock Mechanics & Mining Science, 34, 94.e1-94.e2. http://dx.doi.org/10.1016/s1365-1609(97)00085-3
- Makurat, A., Barton, N., Rad, N.S. and Bandis, S. (1990) Joint Conductivity Variation due to Normal and Shear Deformation. Proceedings of the International Symposium on Rock Joints, Loen, 4-6 June 1990, 538-540.
- Li, B., Jiang, Y.J., Koyama, T., Jing, L.R. and Tanabashi, Y. (2008) Experimental Study of the Hydro-Mechanical Behavior of Rock Joints Using a Parallel-Plate Model Containing Contact Areas and Artificial Fractures. International Journal of Rock Mechanics and Mining Sciences, 45, 362-375. http://dx.doi.org/10.1016/j.ijrmms.2007.06.004
- Nemoto, K., Watanabe, N., Hirano, N. and Tsuchiya, N. (2009) Direct Measurement of Contact Area and Stress Dependence of Anisotropic Flow through Rock Fracture with Heterogeneous Aperture Distribution. Earth and Planetary Science Letters, 281, 81-87. http://dx.doi.org/10.1016/j.epsl.2009.02.005
NOTES
*Corresponding author.








