Open Journal of Geology
Vol.05 No.03(2015), Article ID:54384,8 pages
10.4236/ojg.2015.53008
Determine Stability Wellbore Utilizing by Artificial Intelligence Systems and Estimation of Elastic Coefficients of Reservoir Rock
Habib Akhundi1, Mohammad Ghafoori2, Gholam-Reza Lashkaripour2
1Geology Department, Ferdowsi University of Mashhad, International Branch, Mashhad, Iran
2Geology Department, Ferdowsi University of Mashhad, Mashhad, Iran
Email: Akhundi.habib@stu.um.ac.ir, ghafoori@um.ac.ir, lashkaripour@um.ac.ir
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 30 January 2015; accepted 28 February 2015; published 4 March 2015
ABSTRACT
Rock elastic properties such as Young’s modulus, Poisson̕s ratio, plays an important role in various stages upstream of such as borehole stability, hydraulic fracturing in laboratory scale for observing mechanical properties of the reservoir rock usually using conventional cores sample that obtained from underground in reservoir condition. This method is the most common and most reliable way to get the reservoir rock properties, but it has some weaknesses. Currently, neural network techniques have replaced usual laboratory methods because they can do a similar operation faster and more accurately. To obtain the elastic coefficient, we should have compressional wave velocity (VP), shear wave (Vs) and density bulk due to high cost of (Vs) measurement and low real ability of estimation through the (Vp) and porosity. Therefore in this study, neural networks were used as a suitable method for estimating shear wave, and then elastic coefficients of reservoir rock using different relationships were predicted. Neural network used in this study was not like a black box because we used the results of multiple regression that could easily modify prediction of (Vs) through appropriate combination of data. The same information that were intended for multiple regression were used as input in neural networks, and shear wave velocity was obtained using (Vp) and well logging data in carbonate rocks. The results showed that methods applied in this carbonate reservoir was successful, so that shear wave velocity was predicted with about 92% and 95% correlation coefficient in multiple regression and neural network method, respectively.
Keywords:
Elastic Coefficients, Borehole Stability, Shear Wave Velocity, Petrophysical Logs, Neural Networks, Caliper Log

1. Introduction
Elastic coefficients of reservoir rock are of the basic fundamentals of Geomechanical calculations which knowing them plays a significant role in solving the drilling problems and development of hydrocarbon fields. By knowing elastic coefficients, we can discover some of variable parameters in the reservoir such as pay pressure because reservoir pressure drops irregularly due to the extraction [1] . Therefore, because of balancing physical conditions in the reservoir, we can investigate pressure changes and eventually movement status and migration of the fluid in the reservoir by approximating elastic coefficients of pressure changes in the reservoir.
One of the applications of the geomechanical parameters in petroleum industry is determining the borehole stability. Achieving this purpose requires determining elastic coefficients using compressional wave velocity, density log and shear wave velocity data. Knowing borehole stability is an important point in geology and engineering because formation damage is due to various factors that affect the permeability of the area around the wellbore and thus affects the amount of oil and gas production [2] .
Velocity shear wave through the Dipole Shear Sonic Imager (DSI) tool obtained is one of the most important parameters in Determination elastic coefficients and exploratory studies of Petroleum and gas industry which unfortunately hasn’t been measured in most wells due to high costs. For this reason, numerous methods have been presented to estimate these parameters from other well logging data that are recorded in most wells. Since shear wave velocity is affected from different parameters of the rock (compressional wave velocity, pore fluid and etc.), it could also indicate the physical properties of the rock. Hence, shear wave velocity is used in determining the type of lithology, pore fluid and geomechanical parameters of the formation such as shear modulus, bulk modulus and etc. [3] . DSI is a new tool that directly measures the shear wave velocity, but data of this tool isn’t available in all well especially old wells. Therefore researches have always tried to obtain this information with the minimum cost and using other methods such as well logging data, which are available in most wells. Some of these methods are new statistical techniques and artificial neural networks which could solve issues related to reservoir characteristics and geomechanical parameters that old calculations can’t solve them. Because of unique capabilities of neural network approach, it has been a computational tool in Petroleum industry. Thus prediction of (Vs) in the third well was performed using other logs. Then elastic coefficients of reservoir rock were predicted using compressional wave velocity, density and shear wave velocity data [4] .
In studied Asmari reservoir which is a carbonate oilfield in the Zagros basin (south west of Iran), three well have been selected which two wells have shear wave velocity (Vs) data, compressional wave velocity and data related to petrophysical logs, but the third well haven’t (Vs) data. Thus prediction of (Vs) in the third well, which has generalization capability to entire field, is carried out using other logs. The use of data compression wave velocity, density and shear wave velocity estimated by the neural network, elastic coefficients reservoir rock were predicted.
2. Compressional and Shear Waves
Bulk waves play an important role in petro-acoustical studies and are divided into two categories: compressional waves and shear waves. Relationship between velocity of compressional and shear waves with density and elastic coefficients is expressed as follow:
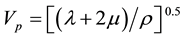 (1)
(1)
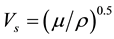 (2)
(2)
where Vp is compressional wave velocity, Vs is shear wave velocity, ρ is rock density, μ is stiffness modulus and λ is Lame constant. One of the most important properties of shear wave is that it cannot travel through the fluids, so it plays a major role in describing reservoir properties.
3. Relations between Shear Wave Velocity and Petrophysical Data
Due to complexity of relationship between (VS) values with all properties of rock and fluid, only important and measurable parameters of rock and fluid properties (that could be obtained through well logging data) were selected as main input parameters of the model. Thus selected parameters should have a significant effect on VS.
Figure 1 show the relationship between various parameters of the input and output (shear wave velocity) of
Figure 1. The relationship between shear wave velocity with neutron porosity (I), density (II), compressional wave velocity (III), gamma ray (IV), the deep resistivity log (V) and shallow resistivity log (VI).
the model. As shown, the conformity between shear wave velocity and well logging is different as the most correlation is between (Vs) and (VP) and the least correlation is between (Vs) and GR.
4. Results and Discussion
4.1. Castagna Method
There are different empirical equations to predict (VS) using petrophysical log data. We studied various empirical equations, which are a combination of different petrophysical parameters for predicting (VS), In order to find out factors which have the most effect on (VS). In addition, compare the relationship between shear wave velocity and other parameters and petrophysical logs (GR, LLS, LLD, VP, NPHI, and RHOB) showed that there is a close relationship between velocities of compressional and shear waves, especially in carbonate rocks (Figure 1). Thus prediction of (Vs) using compressional wave velocity is more reliable, especially in carbonate rocks. Given to the very close relationship of Vs − VP in carbonate rocks, among various empirical equations, we used Castagna equation to predict shear wave velocity. Generally, these empirical relationships only present good results in similar formations and their validation in other rocks is doubtful until it become calibrated. Thus providing a physical model that shows proper understanding of the shear wave behavior would be useful [5] .
In this study, compressional wave velocity (VP) data has been obtained using sonic log (DT) data and through Equation (3). In addition Castagna et al. equations, which is used for limestone and dolomite, is presented below (Equations (4) and (5)):
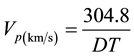 (3)
(3)
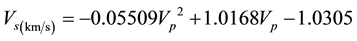 (4)
(4)
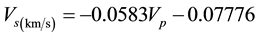 (5)
(5)
Figure 2 shows the result of comparison of (VS) values, which measured and estimated by Castagna relationship for entire the reservoir. This relationship has an input parameter and correlation coefficient of (VS) values, which measured and estimated by Castagna relationship, is about 72% (R2 = 72).
4.2. Multiple Regression Method
Multiple regression analysis uses from correlation between different well logging data and desired parameter. To estimate a parameter in multiple regression, initially this parameter is communicated to several other parameters. The advantages of this technique compared to simple regression are its more accuracy and its capability to summarize more information. It should be noted in using this technique that parameters which are selected for multiple regression should be independent from each other and don’t have a high correlation [6] .
Although previous empirical studies present a proper instruction to select dependent variables, however new prediction equations should be presented for each new region or field. Therefore to identify input data, first we should determine the correlation coefficients between different well logging data by shear wave velocity. Then data that have the highest correlation with shear wave velocity are selected as input data. For this purpose, the correlation coefficients between different well logging data and shear wave velocity were calculated. Then data with high correlation coefficient were selected. According to Figure 2, parameters having the highest correlation coefficient with shear wave velocity are, respectively: data of compressional wave velocity, density, neutron porosity, deep and shallow resistivity and gamma ray, so these six parameters can be used as input to multiple regression.
A multivariate model of the data solves for unknown coefficients a0, a1, a2…, a5 of a multivariate equation such as Equation (6):
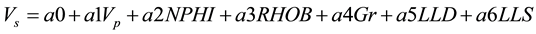 (6)
(6)
Figure 2. The measured shear wave velocity versus shear wave velocity estimated from Castagna relationship.
Weight of input variables to predict (VS) is determined by contribution degree of VS (which characterized by multiple regression). After all variables (LLS, GR, LLD, RHOB, NPHI and VP) were included in the model, the following equation with correlation coefficient of 90% was obtained.
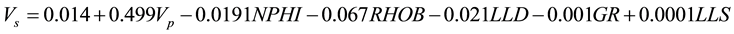 (7)
(7)
The above equation shows that the coefficients of independent variables (NPHI, RHOB and VP) is high and they are important variables of the regression but coefficients of GR, LLD and LLS is low and they are the weakest variables of the model. In this stage, Low-value variables (low coefficients) were removed from the model and the new model was fitted again and the following equation was obtained:
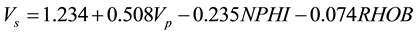 (8)
(8)
When all desired parameters were used, R2 was about 90% but when we removed these three factors (LLD, LLS and GR), the model capability was improved and R2 was increased about 2% and arrived to 92%. Figure 3 shows a good correlation between VS obtained from Equation (8) and the measured VS (R2 is about 92%) and Figure 4 shows the VS calculated from multiple regression and VS obtained from dipole tool versus the depth. The multiple linear regression of the presented variables shows a strong correlation among (VS) values predicted from well logging data.
Figure 3. Correlation between measured shear wave velocity and shear wave velocity estimated by multiple regression analysis.
Figure 4. Correlation between measured Vs and shear wave velocity estimated by multiple regression versus depth.
Both regression method and empirical equations method are acceptable for estimating shear wave velocity using logging data for carbonate reservoir, but regression method usually has smaller error compared to empirical equations method. On the other hand, empirical equations haven’t generalizability for different lithologies. Moreover, in these models, shear wave velocity is a function of a few parameters such as compressional wave velocity and porosity. Considering these limitations, a powerful method, that can overcome these shortcomings, is necessary to estimate shear wave velocity. Therefore, it was proposed to implement smart techniques such as neural networks which have been associated with significant successes.
4.3. Design and Development of the Neural Network
In this study, initially the available data were processed and inappropriate data were omitted, since they have a negative effect on network training and testing. Then, the data were normalized in (0, 1) interval. The best case for neuron networks is when all inputs and outputs are between 0 and 1. Hence, we normalized the input data (well logging data) and output data (DSI data) in (0, 1) interval to perform the network training in the best possible way [7] . Among all processed data (data from wells No. 1, 2 and 3), data from well No. 1 and well No. 2 were selected as the training set and test and validation set, respectively. Then, a three-layer feed-forward neural network was used to build the model. The network components include neurons and layers. Neurons are organized in layers and each layer is responsible for a specific task. Input layer receives information from the environment and transfers it to the middle layer. Middle layer (hidden) analyses the information entered from the environment into the neural network. Output layer receives the result of analyzed information from middle layer and converts them to a meaningful form and returns them into the environment [8] . We used different training algorithms and transfer functions to design a desirable network. Experimentally, it was proved that feed forward networks with error back-propagation algorithm to determine the geomechanical parameters give the best result. Therefore, in order to estimate shear wave velocity, we used error back-propagation algorithm (which is a feed-forward supervised learning algorithm) with TrainLM training function. To avoid excessive network training, a particular set named “validation set” was used. Network validation is performed simultaneously with network training in each course and when validation data error begins to rise, the training is stopped. Mean square error (MSE) curve in terms of the number of training course (Epochs) for training data shows that the network has arrived to the best learning and the lowest error after 198 rounds (Figure 5).
In this study, different input sets with various middle neurons were used to predict Vs. Inputs with the smallest error and the highest correlation coefficient were selected as desirable inputs, and finally the best result was belong to a network with five input parameters (GR, NPHI, RHOB, LLD and VP) and 8 neurons in the middle layer and the values of correlation coefficients for training and testing stages (Figure 6 & Figure 7) was about
Figure 5. Number of iterations (epochs) versus mean square error (MSE).
Figure 6. Cross-plot between measured Vs and Vs estimated by neural networks in training stage.
Figure 7. Cross-plot between measured Vs and Vs estimated by neural networks in testing stage.
R2 = 0.97 and R2 = 0.95, respectively. The above conformity between measured (Vs) and (Vs) predicted through neural network (Figure 8) indicates high capability of neural networks in predicting geomechanical parameters.
According to the above results, the efficiency of artificial neural network in estimating shear wave velocity is very high. Thus, the Vs measured by DSI tool and Vs calculated from neural network are very close and therefore the results of this network could be generalized to the well No. 3, which hasn’t shear wave velocity.
5. Estimation of Elastic Coefficients of the Reservoir Rock
In order to obtain elastic coefficients of the reservoir, we used compressional wave velocity log, density log, shear wave velocity estimated from neural network and equations 9 to 13. Then the log related to obtained elastic coefficient was drawn against the depth and caliper log (Figure 9). We can estimate the borehole stability and deal with zoning the borehole stability in the different depths using the relationship between geomechanical parameters and caliper log [9] . As shown in this figures, drawing elastic logs against the caliper log shows that there is a direct relationship between elastic coefficients and borehole stability. So if the clustering of the elastic coefficients be used, a high quality zoning of the borehole stability would be provide.
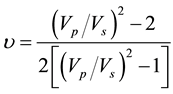 (9)
(9)


Figure 8. Comparison of measured Vs and Vs estimated by neural network versus depth.
Figure 9. The curve of Geomechanical parameters versus depth (right to left to, respectively, Young’s modulus, bulk modulus, shear modulus, Poisson’s ratio) and a direct relationship with caliper logs (blue graph).


6. Conclusions
The obtained results showed that the methods used in this carbonate reservoir were successful as shear wave velocity in multiple regression method and neural network method was predicted with correlation coefficients of 92% and 95%, respectively. Thus, the network designed for the desired well can be used to estimate elastic coefficients in wells around this field, which haven’t shear wave velocity, and use this parameter to describe and develop the petroleum field of study.
Elastic coefficients have a direct relationship with the borehole stability and this is revealed through drawing elastic coefficients logs against caliper log.
By having well logging data for more wells of a field, elastic coefficients can be generalized to entire field and the geomechanical equations―to obtain dynamic behavior of the reservoir―and eventually the status of the pressure and fluid movement in the oilfield could be studied.
References
- Ameen, M.S., Smart, B.G.D., Somerville, J.M.C., Hammilton, S. and Naji, N.A. (2009) Predicting Rock Mechanical Properties of Carbonates from Wireline Logs (A Case Study: Arab-D Reservoir, Ghawar Field, Saudi Arabia). Marine and Petroleum Geology, 26, 430-444. http://dx.doi.org/10.1016/j.marpetgeo.2009.01.017
- Saidi Nia, M. and Shadi Zade, R. (2010) The Effect of Stress Due to Drilling Operations on Well and Skin Factor, Journal of Petroleum Research, 63, 39-48.
- Eskandari, H., Rezaee, M.R. and Mohammadnia, M. (2004) Application of Multiple Regression and Artificial Neural Network Techniques to Predict Shear Wave Velocity from Well Log Data for a Carbonate Reservoir, South-West Iran. CSEG Recorder, 42-48.
- Habimana, J. (2002) Geomechanical Characterization of Cataclastic Rocks. International Journal of Rock Mechanics & Mining Sciences, 39, 677-693. http://dx.doi.org/10.1016/S1365-1609(02)00042-4
- Wang, Z. (2000) Velocity Relationships in Granular Rocks. In: Wang, Z. and Nur, A., Eds., Seismic and Acoustic Velocities in Reservoir Rocks, 145-158.
- Hasanipak, A.A. and Sharafodin, M. (2000) Analyze of Exploration Data. Tehran University Press, Tehran.
- Bhatt, A. and Hell, H.B. (2002) Committee Neural Networks for Porosity and Permeability Prediction from Well Logs. Geophysical Prospecting, 50, 645-660. http://dx.doi.org/10.1046/j.1365-2478.2002.00346.x
- Balan, B., Mohaghegh, S. and Ameri, S. (1995) State-of-Art in Permeability Determination from Well Log Data: Part 1-a Comprehensive Study, Model Development, SPE 30978.
- Sohrabi, S. and Kadkhodaie, A. (2011) Estimate Stability Wellbore Based on the Elastic Coefficients Obtained from Logs. 30th Earth Science Conference, Tehran.














