Open Journal of Geology
Vol.4 No.2(2014), Article ID:43076,11 pages DOI:10.4236/ojg.2014.42004
Frequency Time Analysis (FTAN) and Moment Tensor Inversion Solutions from Short Period Surface Waves in Cameroon (Central Africa)
1Department of Physics, University of Yaounde 1, Yaounde, Cameroon
2Department of Fundermental Sciences, H.T.T.T.C. Bambili-Bamenda, The University of Bamenda, Bambili, Cameroon
Email: ndikumeric@yahoo.com
Copyright © 2014 Eric N. Ndikum et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Eric N. Ndikum et al. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received December 26, 2013; revised January 20, 2014; accepted January 28, 2014
KEYWORDS
Frequency Time Analysis (FTAN); Surface Waves; Group Velocity Dispersion Curves; Moment Tensor Inversion
ABSTRACT
Short period surface waves generated by a local earthquake recorded by broadband seismometers at distances of about 186 to 778 km from the earthquake’s epicenter located in Cameroon (Central Africa) were processed for group velocity maps and dispersion waveforms using the frequency time analysis (FTAN) method. The resulting group velocity fundamental modes of the extracted Rayleigh and Love waves were used for a joint amplitude spectral and P polarity inversion using moment tensor inversion. The corresponding group velocity dispersion curves, the residual as a function of depth, the amplitude spectra and the moment tensor solutions of the regions from the epicenter to the different stations up to a depth of about 10 km were obtained.
1. Introduction
Information on the constitution of the subsurface structure of the earth can be obtained from the studies of elastic waves travelling through the earth which are generated by either natural phenomena like earthquakes and collapse of rock cavities or by artificial means like explosions from nuclear test sites. Also, downand crosshole tests can be used to obtain detailed shear wave (Vs) velocities even though these are very expensive because of drilling costs [1]. Consequently, they can be measured from refraction seismic surveys by studying the dispersion of Rayleigh surface wave group velocities which are related to the signal energy. One very efficient method to study surface waves is the frequency time analysis (FTAN) method which is very useful in defining Vs profiles of shallow geological structures [2] and finds a lot of applications in Seismology. In this paper, FTAN is used to extract group velocity dispersion curves of surface wave fundamental modes resulting from a local earthquake, after which inversion is carried out on the results using the moment tensor inversion technique.
2. Methodology
2.1. Data Acquisition
The surface waves used in this study are extracted from a local earthquake of magnitude Ml = 3.04 which occurred on the 19 of March 2005 at 11:49:18:31 (local time) of intensity VI according to the modified Mercalli (MM) Intensity scale. Its epicenter was located at Monatele (Cameroon) with latitude 4˚26.34' and longitude 10˚59.62' and it had a depth of about 7 km. This earthquake was recorded by 7 broadband seismometers CM06, CM09, CM18, CM24, CM26, CM29 and CM32 (Figure 1); located around Cameroon at epicentral distances ranging from about 186 km to 778 km (see Table 1). These seismometers were among 8 portable broadband seismometers
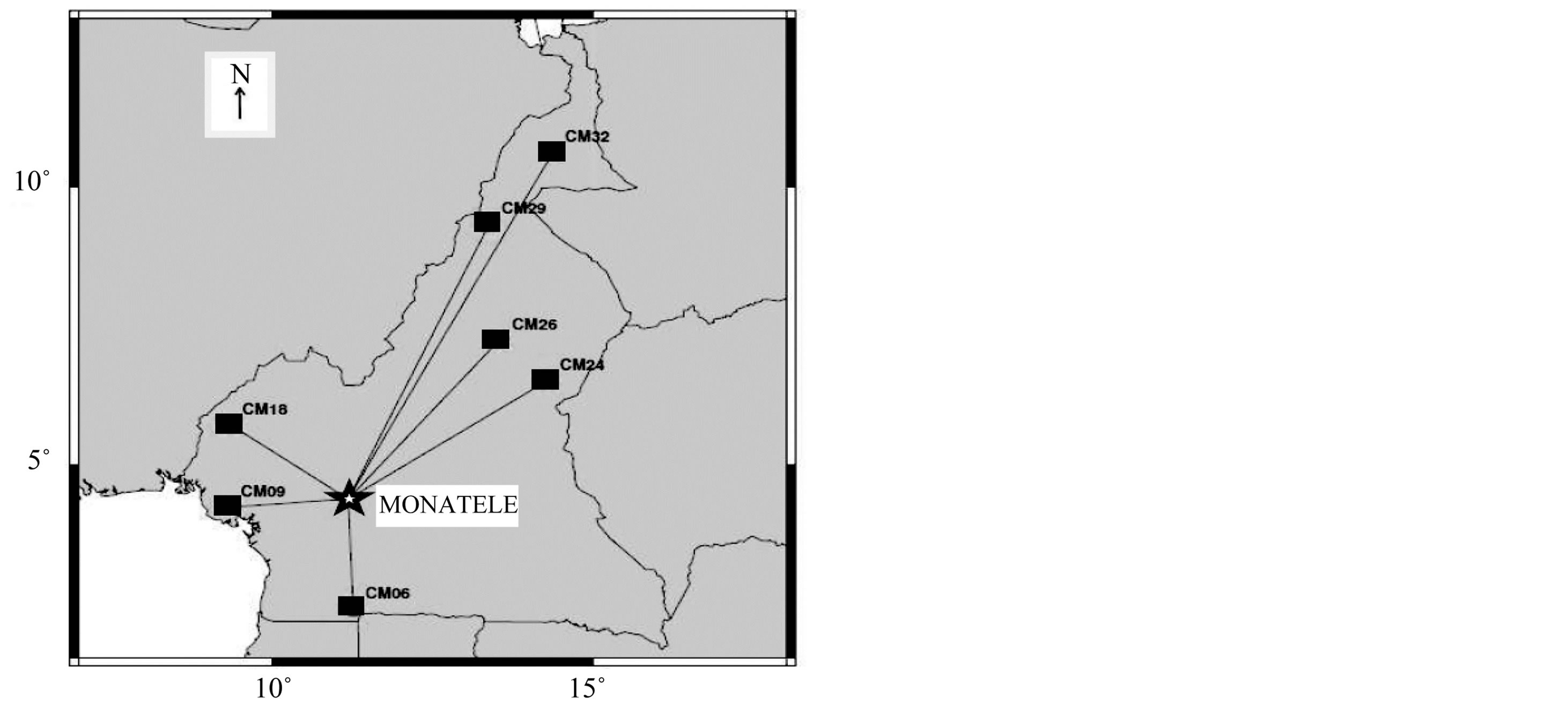
Figure 1. Positions of epicenter (star) of Monatele earthquake and seismic stations (squares).
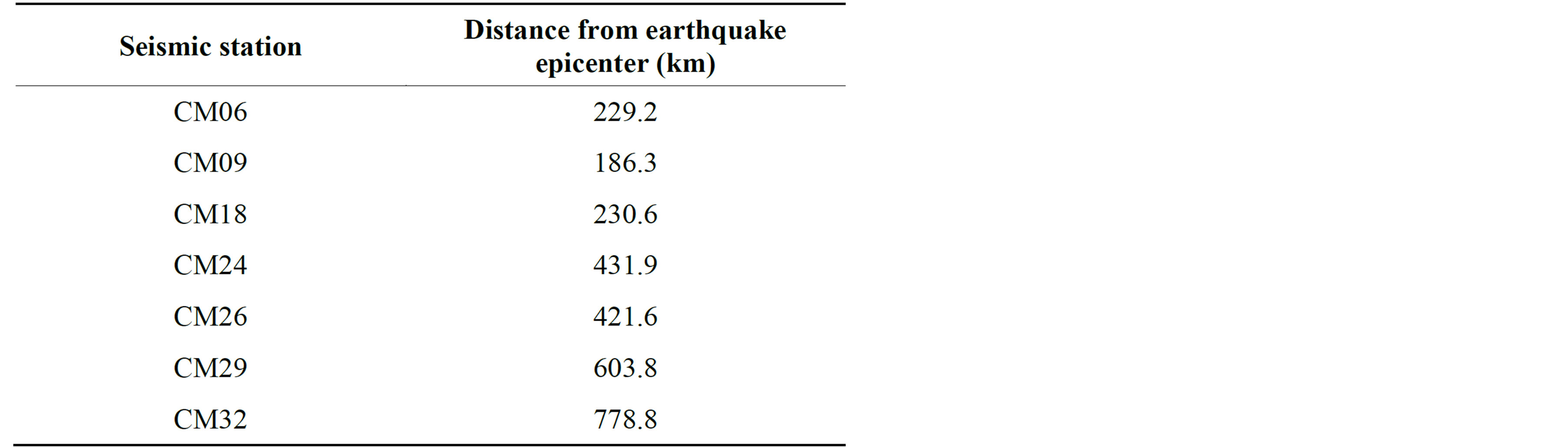
Table 1. Distances of seismic stations from earthquake epicenter.
installed in January 2005 and used in the Cameroon Broadband Seismic Experiment in which studies on the Cameroon Volcanic Line (CVL) were carried out [3]. These 7 seismometers were constituted of two (2) Guralp CMG-3T seismometers, one (1) Guralp CMG-3ESP seismometer and four (4) Streckeisen STS-2 seismometers. They recorded data continuously at 40 samples per second [4].
2.2. The Frequency Time Analysis (FTAN) Method
The frequency time analysis (FTAN) method which was put in place by Levshin and associates [5,6] came to improve in a significant way the multiple filter analysis which Dziewonski and associates originally developed [7]. FTAN can be applied in a setting with only a single channel to measure group velocity even when there is higher mode contamination. When the source is known, the phase velocity can also be measured [2].
This method employs a system of narrow-band Gaussian filters, with varying central frequency, that do not introduce phase distortion and give a good resolution in the time-frequency domain.
For each filter band the square amplitude of the inverse FFT of the filtered signal is the energy carried by the central frequency component of the original signal. Since the arrival time is inversely proportional to group velocity, for a known distance, the energy is obtained as a function of group velocity at a certain central frequency. The process is repeated for different central frequencies. A FTAN map is the image of a matrix whose columns are the energy values at a certain period and the rows are the energy values at constant group velocity. A sequence of frequency filters and time window is applied to the dispersion curve for an easy extraction of the fundamental mode. The floating filtering technique, combined to a phase equalization, permits to isolate the fundamental mode from the higher modes [1,8].
FTAN is useful in defining VS profiles of shallow geological structures and has been applied with great success in both seismological and engineering fields [9-11].
2.3. Moment Tensor & Source Depth Inversion Method
The theory behind Moment Tensor & Source Depth Inversion is summarized below and the details are found in the reference manual of the Moment Tensor & Source Inversion Program which is located in the web site of Surface waves processing & seismic source inversion (double-couple approximation) [12].
The moment tensor M can be used to describe an instant point source. A double couple instant point source at a depth h, can be given by the following: double couple depth, its focal mechanism which is characterized by three angles: strike, dip and slip or by two unit vectors (direction of principal tension T and direction of principal compression P) and seismic moment M0. M0 is determined through the minimisation of the misfit between observed and calculated surface wave amplitude spectra for every current combination of all other parameters. A relationship between the spectrum of the displacements in any surface wave and the total moment tensor M is given as:
 (1)
(1)
where i, j = 1, 2, 3 and the summation convention for repeated subscripts is used,  is the spectrum of Green function for the chosen model of medium and wave type [13,14], with y—source location. The amplitude spectrum
is the spectrum of Green function for the chosen model of medium and wave type [13,14], with y—source location. The amplitude spectrum 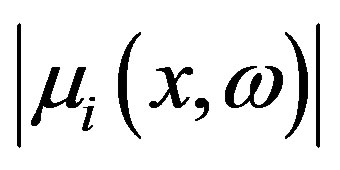 does not depend on the average phase velocity of the surface wave which are usually not well known, as such only amplitude spectra of surface waves are used for determining source parameters under consideration while observed surface wave phase spectra are used only for very long periods. Equation (1) can be used to calculate the amplitude spectra of surface waves. A comparison of calculated and observed amplitudes spectra gives a residual
does not depend on the average phase velocity of the surface wave which are usually not well known, as such only amplitude spectra of surface waves are used for determining source parameters under consideration while observed surface wave phase spectra are used only for very long periods. Equation (1) can be used to calculate the amplitude spectra of surface waves. A comparison of calculated and observed amplitudes spectra gives a residual  for every point of observation, every wave and frequency.
for every point of observation, every wave and frequency.
Surface wave amplitude spectra inversion: If all characteristics of the medium are known the representation (1) gives us a system of equations for parameters defined above. Let us consider now a grid in the space of these 4 parameters. Let the models of the media be given. Using formula (1) we can calculate the amplitude spectra of surface waves at the points of observation for every possible combination of values of the varying parameters. Comparison of calculated and observed amplitude spectra give us a residual  for every point of observation, every wave and every frequency
for every point of observation, every wave and every frequency . For any observed value of the spectrum
. For any observed value of the spectrum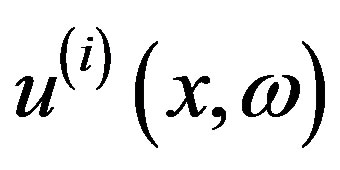 , the corresponding residual
, the corresponding residual  is |
is |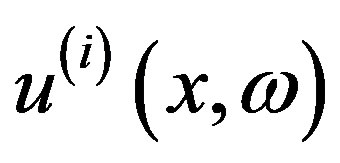 |, where i = 1,…,N; the normalised amplitude residual is defined by:
|, where i = 1,…,N; the normalised amplitude residual is defined by:
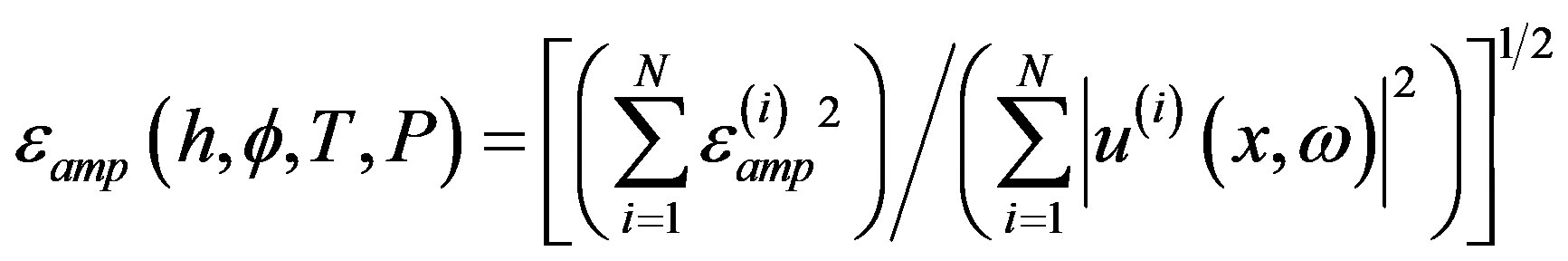 (2)
(2)
The residual can then be defined such that one is a function of a scalar argument , two are a function of vector arguments:
, two are a function of vector arguments: 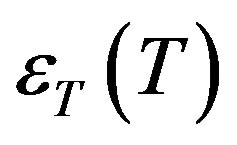 and
and .
.
Since four different focal mechanisms will radiate the same surface wave amplitude spectra, the focal mechanism can not be uniquely determined from surface wave amplitude spectra. Consequently, long period spectra of surface waves or polarities of P wave first arrivals can be used to obtain a unique solution for the focal mechanism.
Joint inversion of surface wave amplitude and phase spectra: For a given frequency range the phase spectra of surface waves at the points of observation for every possible combination of values of the varying parameters can be calculated using Equation (1). When the calculated and observed phase spectra are compared, a residual 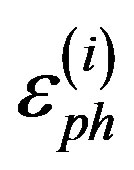 for every point of observation, every wave and every frequency
for every point of observation, every wave and every frequency  can be gotten. The normalised amplitude residual is given by:
can be gotten. The normalised amplitude residual is given by:
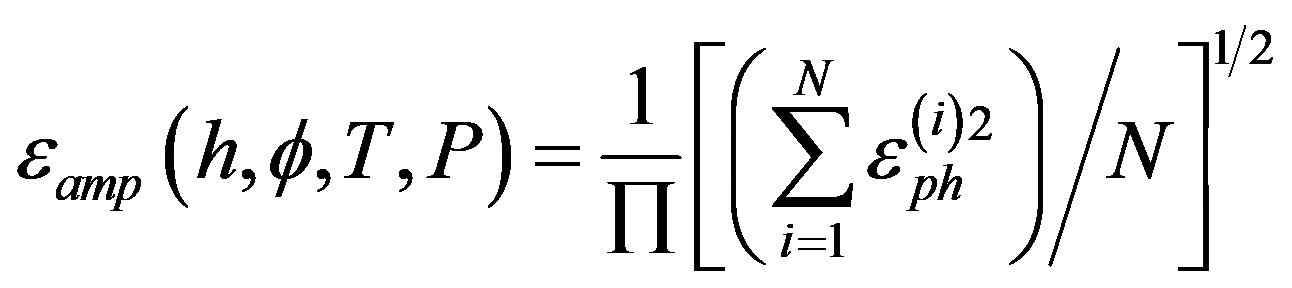 (3)
(3)
The joint residual is given as:
 (4)
(4)
Joint inversion of surface wave amplitude spectra and P wave polarities: When the calculated radiation pattern of P waves for every current combination of parameters are compared with observed polarities, the misfit obtained is used to calculate a joint residual of surface wave amplitude spectra and polarities of P wave first arrivals. if 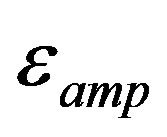 is the residual of surface wave amplitude spectra and
is the residual of surface wave amplitude spectra and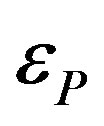 —the residual of P wave first arrival polarities (the number of wrong polarities divided by the full number of observed polarities), then:
—the residual of P wave first arrival polarities (the number of wrong polarities divided by the full number of observed polarities), then:
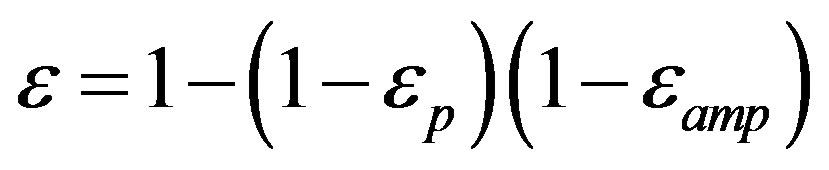 (5)
(5)
3. Data Analysis
The data base creator (dbcreator) program, frequency time analysis (FTAN) program and the moment tensor and source depth inversion program used to analyse data in this paper were obtained from the website of Surface waves processing & seismic source inversion [15].
A seismic database in AH binary file format was created from seismic data in SEED format recorded by the broadband seismometers CM06, CM09, CM18, CM24, CM26, CM29 and CM32 located around Cameroon, Central Africa (see Figure 1) using the dbcreator program. The condition of sampling the database was set such that the input time series was decimated to a binary time series of 1 count per second. This database had a signal length of 120 minutes, being the maximum length provided for by the program.
The FTAN program was then used to process the seismic signal in the database for each station choosing the most appropriate bandpass filtering parameters (see Table 2) that permitted the best extraction of the fundamental mode. To the fundamental mode of each signal, parameters for the right bounds (group velocity and period) for the FTAN diagram were then chosen (see Table 3) in order to extract the group velocity dispersion curve.
This was done using the floating filtering technique combined to phase equalization. For each station, acceptable results of the filtered signal, the amplitude spectra, the FTAN calculated group velocity diagram and the FTAN maps of the filtered seismograms were generated and saved. The different period ranges from floating filtering were saved (see Table 4) to be used for inversion.
The cleaned waveforms of the signals from FTAN were then injected into the moment tensor and source depth inversion program. The period ranges obtained from FTAN were inserted for the corresponding station cleaned waveforms; and then the structural models for the epicentral area and station vicinity were generated by the 3SMAC program (incorporated into the moment tensor and source depth inversion program). The different grid characteristics for the depth, dip, strike and slip were then set where an initial depth of 0 km, a depth step of 1 km and a value of 11 km for the number of depths (allowing for a total depth of 10 km to be attained) were assigned. After the selection and rarefication of polarity data was carried out, the final inversion of the data was then done. The inversion was carried out for both Ray-

Table 2. Bandpass filtering parameters applied on surface waves in FTAN.
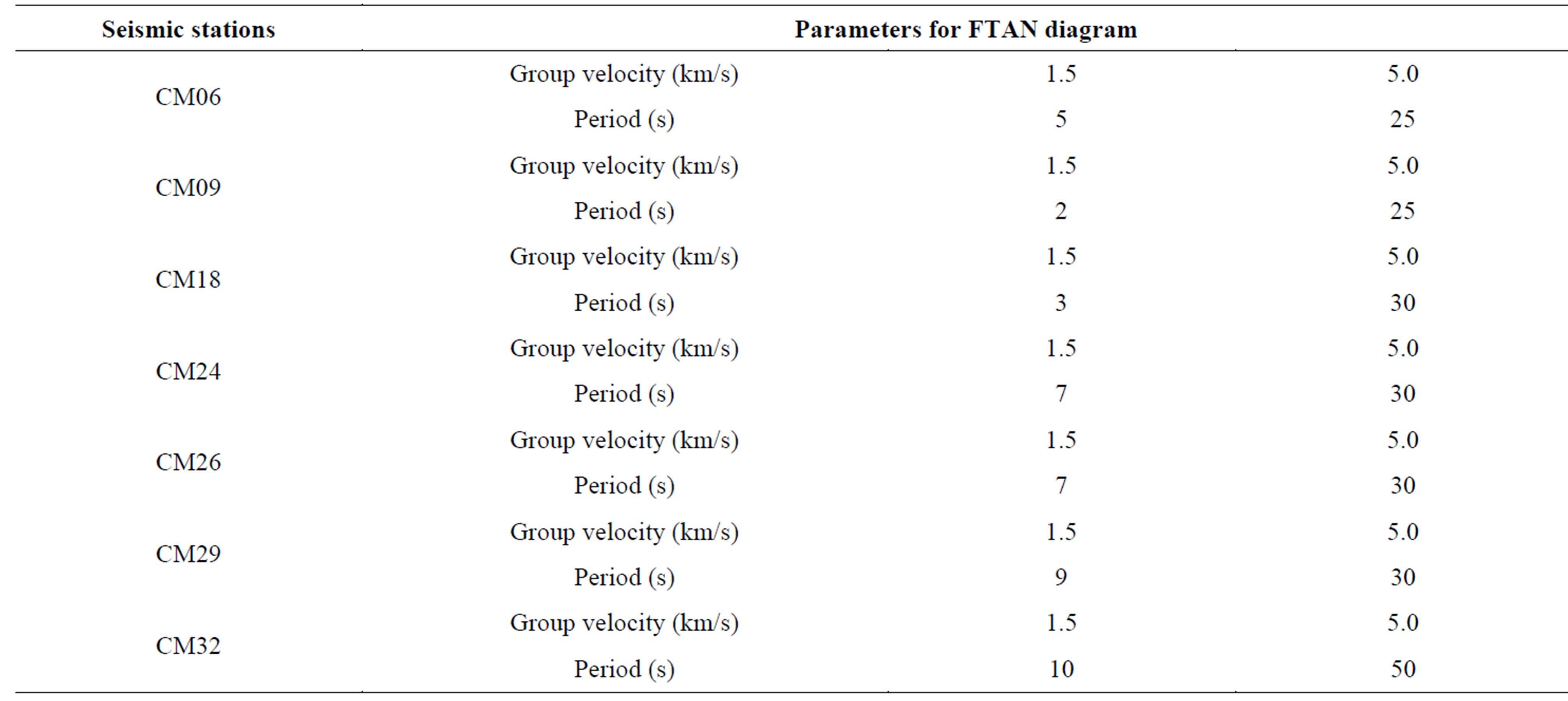
Table 3. Parameters for the bounds of the FTAN diagram.

Table 4. Resulting period ranges from floating filtering.
leigh and Love dispersion waves (with the minimum and maximum time in the spectral range being 7 and 48 s) and then only for the Rayleigh dispersion waves alone (with the minimum and maximum time in the spectral range being 7 and 39 s).
4. Results
When Ftan program was applied to each of the stations using the different parameters for bandpass filteringbounds for the FTAN diagram, and period range shown in Tables 2, 3 and 4, the best solutions for each station was retained. These solutions were saved for the amplitude spectra, the group velocity diagram, the FTAN map and the filtered (cleaned) seismograms. FTAN results were obtained for all the seven stations and the results for station CM18 are presented here in Figures 2, 3, 4 and 5.
When the moment tensor and source depth inversion
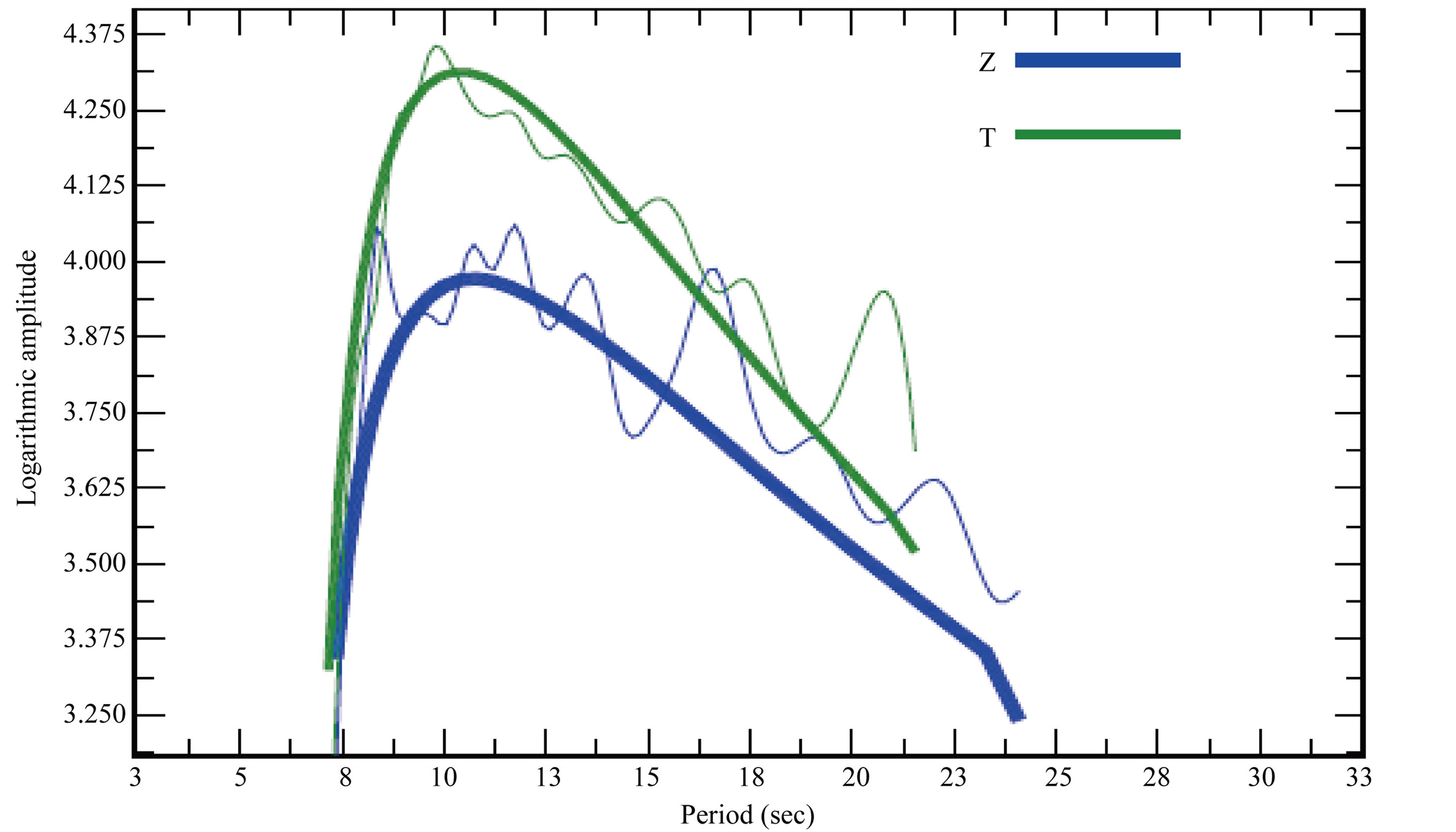
Figure 2. Amplitude spectra for CM18 (thin lines represent the amplitude spectra of raw signals; thick lines represent the amplitude spectra of cleaned signals).
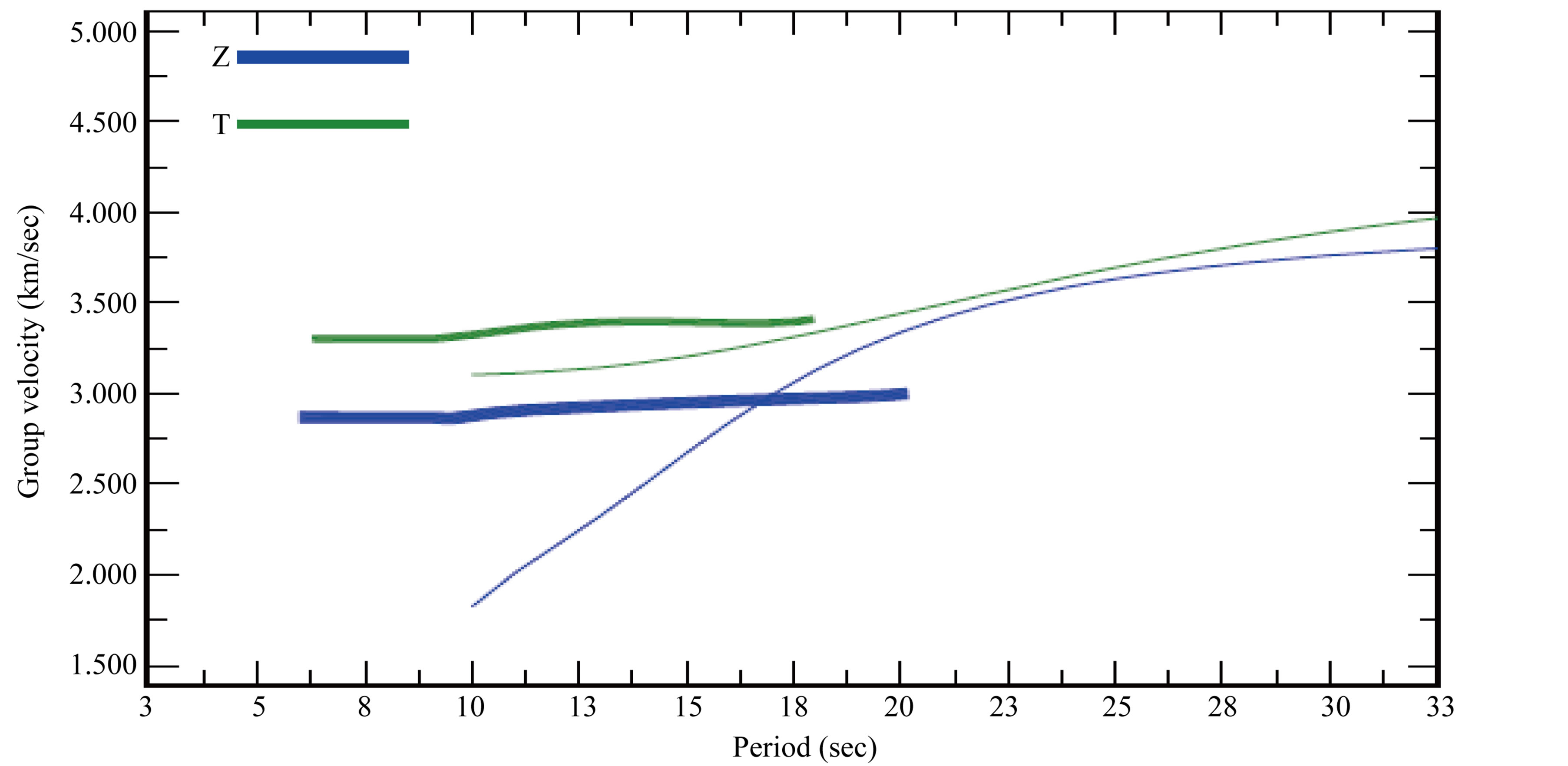
Figure 3. Group velocity plotting for CM18 (thin lines present the amplitude spectra of raw signals; thick lines present the amplitude spectra of cleaned signals).


Figure 4. Plot of filtered signals for CM18 (red for Rayleigh and green for love) and raw signal (blue).
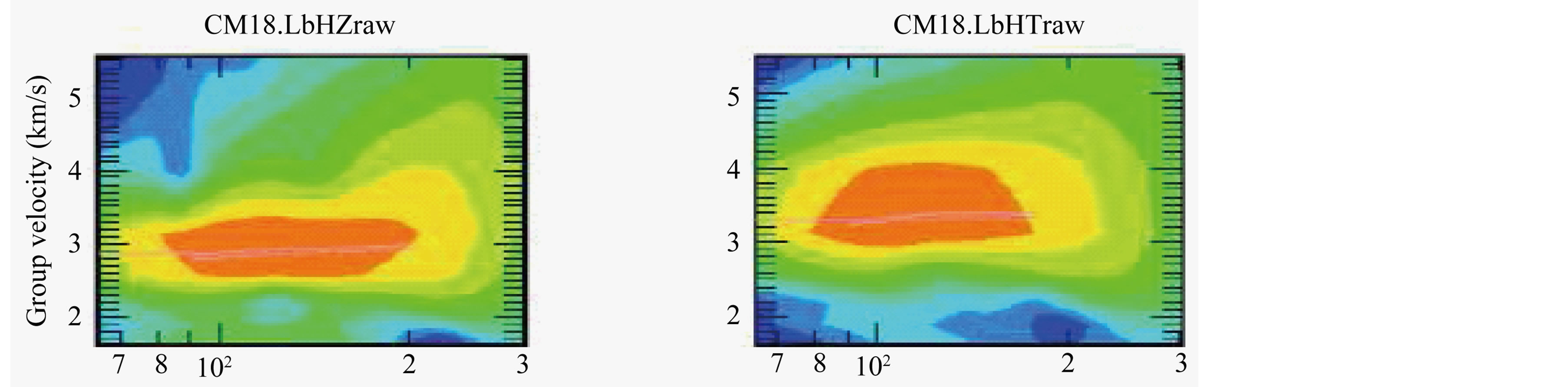


Figure 5. FTAN diagrams from CM18 for cleaned records (below) and raw records (above).
program was applied on the dispersion signals from both the Rayleigh and Love waves, the selection and rarefication of polarity data were carried out at angles of polarity data smoothing of 1, 5 and 10 degrees, but all the results from these were the same. In the case where the moment tensor and source depth inversion program was applied to both Rayleigh and Love waves, results of amplitude spectra inversion and those of joint amplitude spectra plus P polarity inversion were obtained (for the polarities before and after selection and rarefication, the residual as a function of source depth, the spectral residual map for main stress axis, and moment tensor solutions) and presented in Figures 6(a), (b), (c), (d) and Figures 7(a), (b), (c), (d) respectively.
In like manner, for the case where the moment tensor and source depth inversion program was applied to only Rayleigh waves, results of amplitude spectra inversion and those of joint amplitude spectra plus P polarity

Figure 6. Results of amplitude spectra inversion on both Rayleigh and love waves: (a) Plot of polarities before and after selection and rarefication; (b) Plot of residual as function of source depth; (c) Plot of residual for main stress axis; (d) Representation of the best moment tensor solutions.
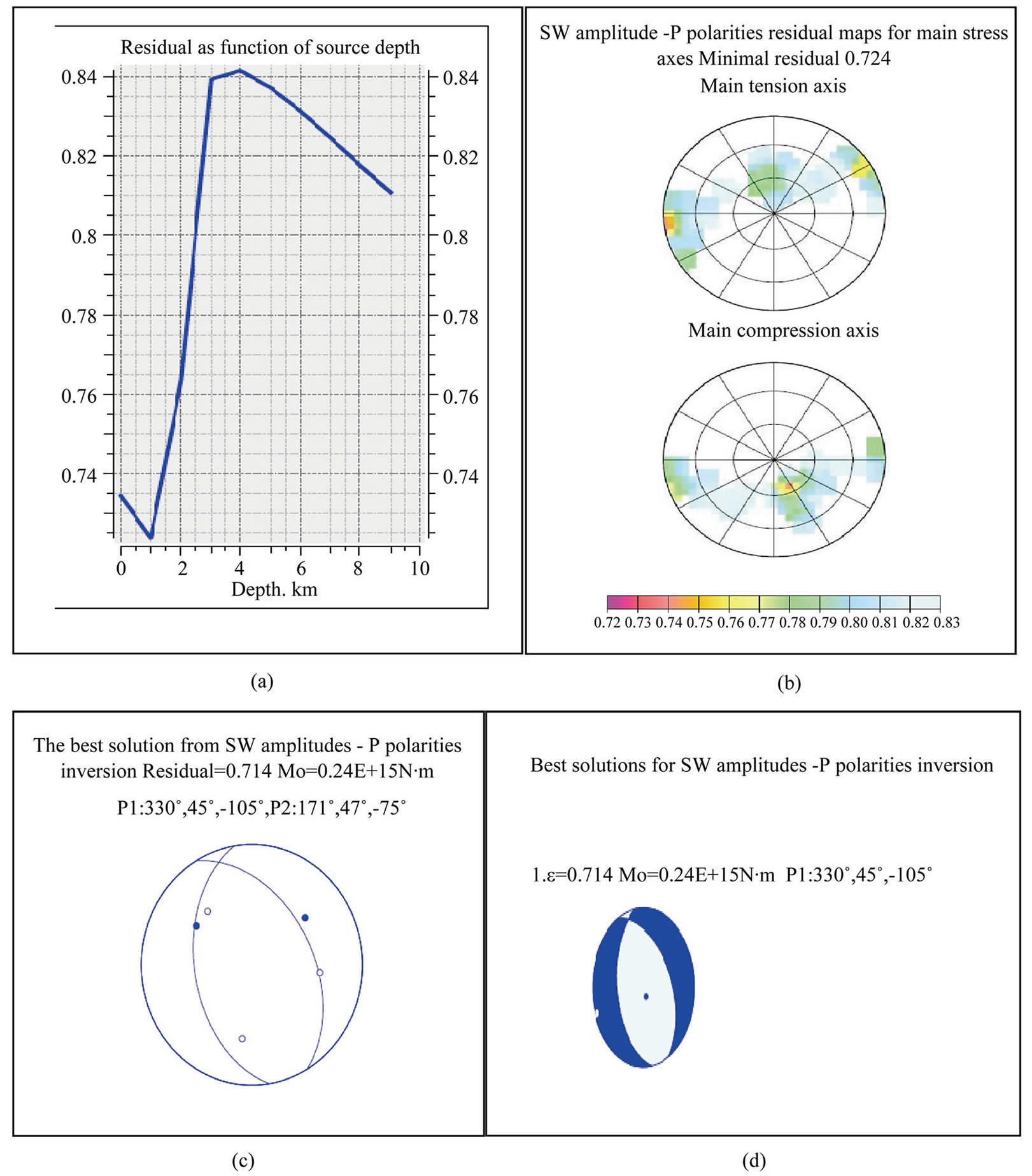
Figure 7. Results of amplitude spectra plus P polarity inversion on both Rayleigh and love waves: (a) Plot of residual as function of source depth; (b) Plot of residual for main stress axis; (c) and (d) Representation of the best moment tensor solutions.
inversion were also obtained and presented in Figures 8(a), (b), (c), (d) and Figures 9(a), (b), (c), (d) respectively.
5. Discussion of Results
The results from moment tensor inversion presented in Figures 6(a), (b), (c), (d) to 9(a), (b), (c), (d) above indicate that for an inversion carried out on both Rayleigh and Love waves, surface wave amplitude spectral inversion has residual and scalar seismic moment (Mo) values of 0.706 and 0.24E+15 Nm respectively, while the joint surface wave amplitude plus P polarity inversion has residual and scalar seismic moment values of 0.714 and 0.24E+15 Nm respectively. On the other hand, in the case where only Rayleigh waves were used, the residual and scalar seismic moment of surface wave amplitude spectral inversion are 0.343 and 0.43E+15 Nm respectively, while the residual and scalar seismic moment for the joint surface wave amplitude plus P polarity inversion are 0.714 and 0.24E+15 Nm respectively. Generally,

Figure 8. Results of amplitude spectra inversion on Rayleigh waves only: (a) Plot of polarities before and after selection and rarefication, (b) Plot of residual as function of source depth, (c) Plot of residual for main stress axis, (d) Representation of the best moment tensor solutions.
it can be noticed that results of the amplitude spectra inversion were improved upon by the joint amplitude spectra and P polarity inversion as far as the precision in moment tensor solutions generated is concerned.
6. Conclusion
After using the FTAN program to extract the surface wave fundamental mode and the group velocity dispersion curves, on which the moment tensor and source depth inversion program is applied, the moment tensor inversion solutions resulting from the joint amplitude spectra and P polarity inversion, in both the case where only the Rayleigh waves were processed and when the Rayleigh and Love waves were processed, gives residual

Figure 9. Results of amplitude spectra plus P polarity inversion on Rayleigh waves only; (a) plot of residual as function of source depth, (b) plot of residual for main stress axis, (c) and (d) representation of the best moment tensor solutions.
and scalar seismic moment (Mo) values of 0.714 and 0.24E+15 Nm respectively.
REFERENCES
- M. Natale, C. Nunziata and G. F. Panza, “FTAN Method for the Detailed Definition of vs in Urban Areas,” 13th World Conference on Earthquake Engineering, Vancouver, 1-6 August 2004, Paper No. 2694.
- J. Boaga, “Seismic Noise and Controlled Source Surveys: Tools for Seismic Hazard Deterministic Approach,” Ph.D. dissertation, University of Padova, Padova, 2008.
- G. G. Euler, D. A. Wiens, P. Shore, F. W. Koch, R. Tibi, A. A. Nyblade and A. M. Reusch, “Shear Velocity Structure of the Cameroon Volcanic line Region from Rayleigh Wave Phase Velocities,” EOS, Transactions, American Geophysical Union, 89(53), AGU Fall Meeting Suppl., 2008, Abstract #S21C-1843.
- K. A. P. Tokam, C. T. Tabod, A. A. Nyblade, A. Julia, D. A. Weins and M. E. Pasyanos, “Structure of the Crust Beneath Cameroon, West Africa, from the Joint Inversion of Rayleigh Wave Group Velocities and Receiver Functions,” Geophyiscal Journal International, Vol. 183, No. 2, 2010, pp. 1061-1076. http://dx.doi.org/10.1111/j.1365-246X.2010.04776.x
- A. Levshin, V. F. Pisarenko and G. A. Pogrebinsky, “On a Frequency-Time Analysis of Oscillations,” Annales Geophysicae, Vol. 128, No. 2, 1972, pp. 211-218.
- A. Levshin, L. I. Ratnikova and J. Berger, “Peculiarities of Surface Wave Propagation across Central Eurasia,” Bulletin of the Seismological Society of America, Vol. 82, No. 6, 1992, pp. 2464-2493.
- A. Dziewonski, S. Bloch and M. Landisman “A Technique for the Analysis of Transient Seismic Signals,” Bulletin of the Seismological Society of America, Vol. 59, No. 1, 1969, pp. 427- 444.
- L. I. Ratnikova, “Frequency-Time Analysis of Surface Waves,” In: Workshop on Earthquake Sources and Regional Lithospheric Structures from Seismic Wave Data, International Centre for Theoretical Physics, Trieste, 1990, pp. 1-12.
- C. Nunziata, G. Costa, M. Natale and G. F. Panza, “FTAN and SASW Methods to Evaluate vs of Neapolitan Pyroclastic Soils,” Earthquake Geotechnical Engineering (Balkema), Vol. 1-3, 1999, pp. 15-19.
- C. Nunziata, G. Costa, M. Natale, A. Vuan and G. F. Panza, “Shear Wave Velocities and Attenuation from Rayleigh Waves,” In: Pre-Failure Deformation Characteristics of Geomaterials (Balkema), 1999, pp. 365-370.
- C. Nunziata, G. Costa, M. Natale and G. F. Panza, “Seismic Characterization of the Shore Sand at Catania,” Journal of Seismology, Vol. 3, No. 3, 1999, pp. 253-264. http://dx.doi.org/10.1023/A:1009861824955
- A. Z. Mostinskiy and B. G. Bukchin, “Moment Tensor & Source Depth Inversion Program Reference Manual, Surface Waves Processing & Seismic Source Inversion,” International Institute of Earthquake Prediction Theory and Mathematical Geophysics (Mitpan), On-Line Bulletin, 1998-2005. http://www.mitp.ru/en/soft/word_pdf_Manuals/MomTens_man.pdf
- A. L. Levshin, “Effects of Lateral Inhomogeneity on Surface Wave Amplitude Measurements,” Annles Geophysicae, Vol. 3, No. 4, 1985, pp. 511-518.
- B. G. Bukchin, “Determination of Source Parameters from Surface Waves Recordings Allowing for Uncertainties in the Properties of the Medium,” Izvestiya Physics of the Solid Earth, Vol. 25, 1990, pp. 723-728.
- A. Z. Mostinskiy, B. G. Bukchin and A. A. Egorkin, “Software Packages for Data Base, Frequency-Time Analysis Program and Moment Tensor & Source Depth Inversion Program (FMT package), Surface Waves Processing & Seismic Source Inversion (Double-Couple Approximation),” International Institute of Earthquake Prediction Theory and Mathematical Geophysics (Mitpan), On-Line Bulletin, 1998-2005. http://www.mitp.ru/en/soft/mainIndex.html
NOTES
*Corresponding author.

