Open Journal of Geology
Vol. 3 No. 3 (2013) , Article ID: 33924 , 12 pages DOI:10.4236/ojg.2013.33019
Fractal Analysis of Lineaments in Equatorial Africa: Insights on Lithospheric Structure
1Isotopic Geochemistry and Chemical Geodynamics Laboratory, DSTE (CP 160/02) Université Libre de Bruxelles (ULB), Bruxelles, Belgique
2Institut des Hautes Études Scientifiques, Le Bois-Marie, Bures-sur-Yvette, France
3UMR CNRS 6250 (LIENSs), ILE, Université of La Rochelle, La Rochelle, France
4UMR CNRS 6112 (LPGN), Université of Nantes, Nantes, France
Email: *cnkono@ulb.ac.be
Copyright © 2013 Collin Nkono et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received March 2, 2013; revised April 10, 2013; accepted May 5, 2013
Keywords: Lineament; Fractal Analysis; SRTM; Equatorial Africa
ABSTRACT
In this paper, the complexity in the spatial distribution of the lineaments was investigated from on remote sensing topographic (SRTM DEM) and multispectral (Landsat) data. Lineaments in equatorial Africa were chosen to apply the fractal analysis methodology. The good correlations of the obtained data with some geophysical data from the same area allow that the complexity in the spatial distribution of the lineaments can give qualitative information on the interior of the earth (or on other planets). This method can provide a bridge between classical geology and geophysics, and particularly powerful for studying large and inaccessible regions.
1. Introduction
The complexity in the spatial distribution of the lineaments studies is nowadays increasingly used in geosciences [1-13]. The concept of lineaments covers a very wide range of geological phenomena, from plate boundaries on the order of thousands of kilometres, to micronsized fractures in mineral grains. [2,3] defined three steps for the Lineament 1) identification and documentation (automatically or manually) of lineament features seen in a given data set in the form of lines; 2) extraction of the properties that are represented by these lines; 3) interpretation of the geoscientific meaning of these properties and of the lineaments as such.
For the spatial extraction, several approaches are possible. We choose the method based on a subsequent sampling of properties within a defined 1˚ square grid (110 km aside), commonly practiced for lineaments derived from satellite data. The gird size was chosen according to the Nyquist criterion, that the sampling size must greater than the object dimension. A 1˚ square size for the grid is a good compromise between the feature dimension and the spatial resolution of the remote sensing topographic (SRTM DEM) and multispectral (Landsat) data.
In this study, we investigate the complexity in the spatial distribution of the lineaments obtained by the analysis of satellite images centred on the Cameroon Line (equatorial Africa). All lineaments are included and treated individually to derive statistical distributions of the length, and globally to derive Local Fractal Dimension (LFD), and intersection points. The length is the distance between the start and end lineaments borders, scaled to a systematic unit (km). The complexity in the spatial distribution of the lineaments was expressed: as the cumulate length of lineaments per unit area, as LFD per unit area, and as the intersection points, respectively.
A previous study of fractal analysis of the lineament in equatorial Africa was done by [8] from aerial photographs. At contrast to [8] who estimated a unique fractal dimension for the entire region, we have partition the field area in grid cell of 1˚ square (110 km aside) to calculate a Local Fractal Dimension (LFD) which is out of reach of the conventional fractal analysis (i.e. global analysis determining a unique fractal dimension: [6-12] for each grid cell.
This area has been selected because we have Precambrian belt (south of Cameroon), sedimentary (Benue Trough), and igneous rock (southern part of Cameroon Volcanic Line). After the geological setting of the studied area, the methodology is presented with a brief description of the software, and how we used it. The results are presented and then compared to the geophysical data.
2. Geological Setting
The magmatic units in the study area are the Cameroon Volcanic Line, Biu and Jos Plateau. The CVL is a complex tectono-magmatic structure extends for more than 2000 km across the Gulf of Guinea and the African Continent, mainly in Cameroon, up to Lake Chad. It has a NNE orientation.
In literature numerous hypotheses have been proposed to explain the structure and the formation of the CHL (see [4,14-23]). The most widely accepted structural explanation is that the CVL would be a succession of “en-échelon” mega-tension gashes, resulting from the reactivation during Aptian-Albian times of the N70E shear zone associated faults at the onset of opening of the Central Atlantic Ocean (e.g. [18]). A recent review of the petrological, geochemical and isotopic data ([23]) reinterprets the CVL as a mantle hot line, the “Cameroon Hot Line” (CHL).
The continental sector of the CHL is of y-shaped form; sometimes in literature the Biu Plateau is consider as the end of the NNW branch of the continental sector of the CHL. [24] shown that, the timing of the Jos Plateau volcanism is very similar to other CHL volcanic centers (Figure 1). The Jos plateau is located 400 km to the NW of the CHL axis (Figure 1). The volcanic activities append during two periods; the first period range from 213 Ma to 147 Ma, and consist of a ring with approximately 30 anorogenic complexes (alkaline affinity); the second period range from 2.1 Ma to 0.9 Ma and consist of 20 cinder cones (basaltic affinity).
According to [24,25], the Biu Plateau mainly overlies granitic basement rocks, whereas to the West and the North, basalts of the Biu Plateau have spread over Cretaceous sediments. They suggest that the Biu Plateau was constructed in a poly stages model with succession of at least two periods of volcanism: 1) An early fissure type eruption and 2) formation of relatively large volcanoes in the southern part of the plateau.
The sedimentary part of the studied area is represented by the Benue basin, it is well over 1000 km long and 700 km wide and is geographically divided into three segments: the Lower, Middle and Upper Benue Trough. Earlier work on the geodynamic evolution and structure of the Benue Trough show that its origin is linked to an Early Cretaceous opening of a rift structure related to a late tectono-magmatic phase [26,27]. [28] demonstrated that the principal structures of this trough are grabens, horsts and half-grabens, whose individual dispositions are controlled by mostly north-south-trending normal faults and northeast-southwest strike-slip faults.
The Precambrian part is located at the southern Cameroon and is part of the Paleoproterozoic West Central African belt (WCAB) [29]. It is running through Congo, Gabon and Cameroon that resulted from a poly-phased continental crustal accretion during the Eburnean orogeny (Figure 1). [30,31] characterized the WCAB by a tectonic reworking of Archean crust with no ocean opening and no addition of juvenile material for Gabon. This interpretation is supported, particularly in Cameroon, by geochemical and isotopic data from the Nyong series, which point to the predominance of crustal recycling processes [32,33].
3. Methodology
This study is focused on analysis of lineaments, the observed lineaments and other topographic objects on the shaded relief models were manually digitized and plotted on the screen by using graphic software. There are many ways to form linear features in a geological environment. Linear features can be all related to brittle features as faults, joints, and dykes, steep to vertical strata or even anthropic features such as roads. All potential lines need to be viewed with caution and subdivided into categories with different degrees of confidence. The choice of a 1˚ square as base unit (kilometer-scale: 110 km × 110 km) of investigation, and the combination of DEMs and Landsat images allow one to constrain linear and circular features of geomorphological origin. Here, the linear features referred to as lineaments will only be those of geological (lithological and/or structural) origin.
3.1. Remote Sensing Mapping
Shuttle Radar Topography Mission (SRTM) Digital Elevation Models (DEMs) are a homogeneous 3-arc-second (~90 m) spatial-resolution topographic dataset with near global coverage (from 60˚N to 56˚S). SRTM data were acquired by the radar system onboard the Space Shuttle Endeavour, during an 11-day mission in February 2000. SRTM DEMs are freely available on the Internet and can be visualized with standard map viewer software. Gaps in the SRTM data occur for steep terrains due to shadows in the radar sight angles.
3.2. Software Used
The lineaments were processed by using Surfer® 8.02 (Golden Software) and controlled against the Landsat images. This software was used to get the shaded relief model showing the terrain under an artificial illumination, with bright sides and shadows. These maps use colors to indicate the local orientation of the surface relative to a user-defined light source direction (the orientation of each grid cell), which is inferred from the calculated
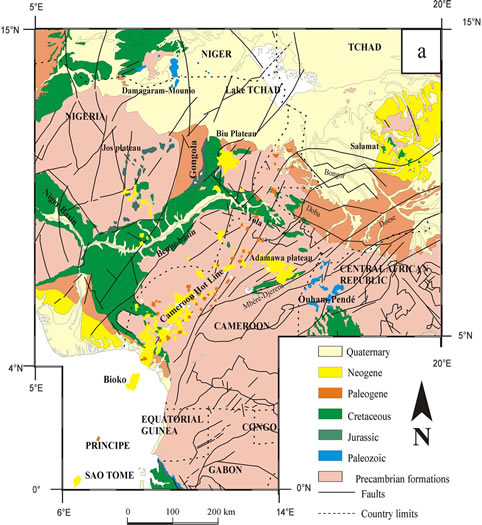
Figure 1. Simplified general geological map of Cameroon indicating the main geological units (BRGM 2004).
reflectance of a point light source on the grid surface. Many types of maps used in this work can be extracted from the original altimetry database, such as, for example: a three-dimensional view: it is a perspective view of the terrain from a user-defined position above the terrain. This view is a digital elevation model displayed as a raster “blanket” in three dimensions. The user can specify the sighting parameters to define the perspective of the observer in relation to the 3D model (Figure 2a). The light source can be thought of as the sun shining on a topographic surface. Portions of the surface that face away from the light source reflect less light towards the viewer and thus appear darker. The rotation angle is 0˚ and the projection is orthographic.
[34,35] have developed and illustrated SPO2003 software through the study of a rock image analysis method. They digitized the image while differentiating the individual phases, each one being given a specific numerical code. The image was then processed by a search algorithm of all neighboring pixels with the same code. The resulting maps are based on the presence of sudden slope-angle changes (or slope breaks), that can be due to lithological differences, topographic differences, or to the presence of thrusts or of faults (Figure 2b). Before analyzing lineament map, we attribute different color to each lineament; convert the resulting map in bmp type, then process the SPO2003 software. There are many parameters in the results table (azimuth, big and small axis.) We use the big axis of lineaments to calculate their length. The SPO2003 software (described in [4,5,34-36]), was used to analyze the distribution, in term of lineament length.
The LFD (Figure 2c) of lineament in each cell has been determined using the Fractalyse2.4.1 software developed within the team “City, mobility, territory” of ThéMA (Théoriser et Modéliser pour Aménager) of University of Franche-Comté in Bourgogne (France). This software, originally developed for estimating the fractal dimension of the built area of cities, can also be used to calculate the fractal dimension of a curve or a fault network. This software proposed dual options for performing a fractal analysis of an image or set of data can be considered: 1) the first is to vary the observation window r at a fixed resolution ε (pixel size), and count the number N(r) of blacks pixels; 2) the second is to fix the observation window and to vary the resolution (apparent pixel size) ε, and count the number N(ε) of ε-pixels occupied by the structure limited by the observation window (grid method) or the number N(ε) of ε-pixels required to cover the structure (box method). The difference between the values of the fractal dimensions obtained by these two methods lies between 0.01 and 0.05. This difference is small, so we consider only the values derived by applying the first calculation option. This difference is small, so we consider only the values derived by applying the first calculation option.
We used the grid partitioning method to estimate fractal dimension. The image is covered by a square grid and the grid mesh size ε is then varied (Figure 2c). The next stage of the measure is to fit an empirical curve from the results of the counting method. Because an image is not a pure fractal (it is not a continuous structure but a discrete one spanning a finite range of scales), it is only possible to get an approximate fractal law.
An important point is that the fractal analysis could not be performed on all elementary cells because lineaments are not always visible, a limit due to the SRTM 3-arc image quality, having a resolution of about 270 m. For more information on its mathematical basis, see the articles of the ThéMA laboratory [37-40].

Figure 2. a) Topographic map around the Adamawa plateau, the calibration of the colour scale is made as a function of altitude ranging from 0 m in the Atlantic Ocean to 4100 m on Mt Cameroon; b) Map of lineaments (straight continuous lines) drawn from the SRTM images; c) Fractal Dimension with fixed of the observation window and to vary the resolution (apparent pixel size) ε, and count the number N(ε) of ε-pixels occupied by the structure limited by the observation window (grid method).
4. Results and Discussion
The observed lineaments as linear objects observed in each 1˚ square were manually digitized and plotted on the screen by using graphics software. The distribution of lineaments results of all the 1˚ square were combined on Figure 3. There are some blankets square without lineaments; these are cover by sedimentary unit. The lineaments were analysed and counted by orientation sector of 5˚ (Figure 3b).
The next analysis step of the lineament network was to calculate the total length. The SPO2003 software was used to calculate the length of each lineament, this allow us to have in each 1˚ square the cumulate length of lineaments. The result of cumulate length analysis of the lineament in the studied are is represent on Figure 4. The spatial distribution of cumulate length is represented as a graded map with different colors corresponding to different ranges of values, in order to give a general view of
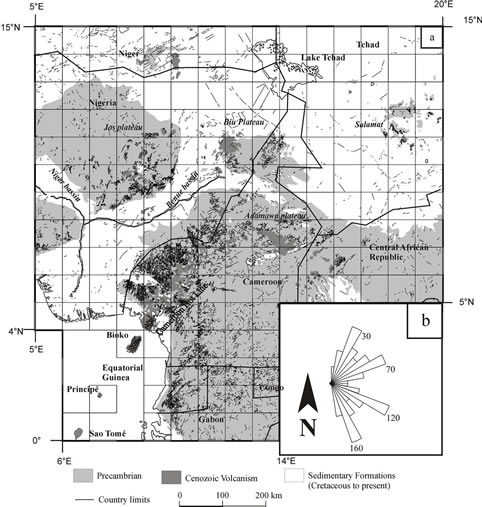
Figure 3. a) Map of lineaments (straight continuous lines) drawn from the SRTM images. Regional geology has been simplified, indicating only Precambrian formations (light grey) Cainozoic volcanism (dark grey) and sedimentary formations (white); b) Rose diagram obtained by the analysis of lineaments (analysis was made every 10˚); the numbers indicate the directions (in degrees).
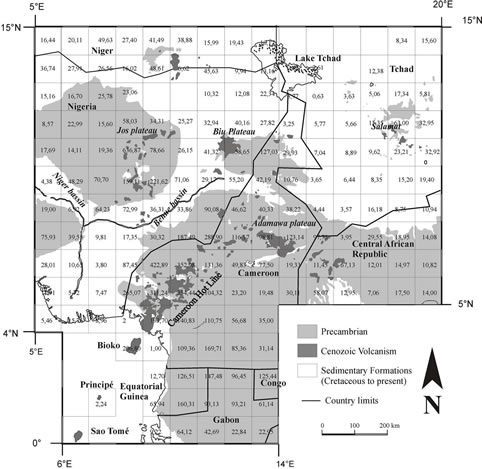
Figure 4. Spatial distribution of the lineament cumulate length on each 1˚ square grid cell on a simplified regional geological map: Precambrian formations (light grey) and recent Cainozoic volcanism (dark grey) and sedimentary formations (white). The number in each grid cell represents the cumulate length in km obtained by analyzing lineaments in this area.
the studied area (Figure 5). The maximum of lineaments length are situated in the Jos plateau (eastern of Nigeria) and in the southern part of the Cameroon Hot line.
The lineament network were analysed by fractal method (Fractalyse2.4.1) for the spatial distribution of the LFD (Figure 6). The spatial distribution of the LFD is represented as a graded map with different colours corresponding to different ranges of values, in order to give a general view of the studied area (Figure 7). LFD is used here to quantify the complexity of the spatial distributions of lineaments. The maximum of LFD are in the south of Gabon and in the southern part of the Cameroon Hot line. On this graded map, we can easily see the direction of the Adamawa plateau, and the extension of the Central African Shear Zone in Cameroon.
The obtained results described above were compared to some geophysical data of the studied area. For the latter, we use:
1) The results from [41] they infer geophysical signature of geological units by the analysis of the geoid map
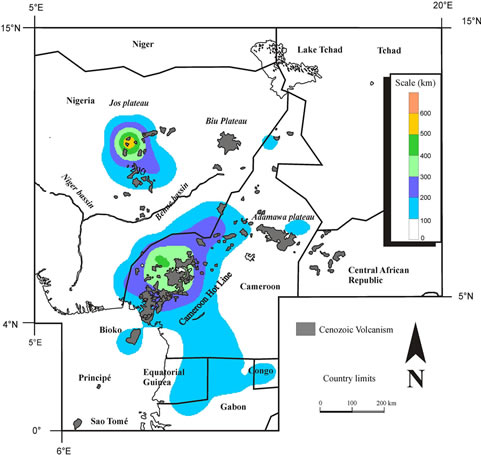
Figure 5. Intensity map of spatial distribution of the cumulate length represented as curves of iso-values, on a simplified (recent Cainozoic volcanism) map.
in central part of the studied area;
2) The diffraction tomography data of [42] to determine the variation of lithosphere thickness at the depth of Moho + 10 km. They used the variation of S-wave velocity to infer the lithospheric structure. Areas with thick and cold lithosphere are characterized by higher S-velocity than areas with thin and hot lithosphere.
In Figures 8a and b, we compare our graded cumulate length map to the Geoid map [41] of Cameroon and part of the adjacent countries, contoured at 0.5 m intervals. On this map the authors identified two geoid highs in Nigeria and in Cameroon. Their areas correspond to our two maximum of the cumulate length in the studied area.
The results obtained on the LFD of the lineament are compared with geophysical data of the studied area (Figures 8c and d). For the latter, we use the data diffraction tomography of [42] to determine the variation of lithosphere thickness at the depth of Moho + 10 km. The LFD density map was modified to be easily superposed on the geophysical map (Figure 8d). Following the superposition, it’s observed that the areas corresponding to yellow colour, with low wave velocity corresponds to the high values of LFD. This means that the maxima of the LFD roughly correspond to areas of thinner lithosphere, and to more reactivate area (sedimentary and igneous). In contrast the areas with high wave velocity correspond to

Figure 6. Spatial distribution of the LFD of lineaments on a simplified regional geological map: Precambrian formations (light grey) and recent Cainozoic volcanism (dark grey) and sedimentary formations (white). The number in each grid cell represents the LFD obtained by analyzing lineaments in this area.
the low values of the LFD, and roughly correspond to the more stable (Precambrian) area. The good correspondence between the geophysical maps and the results obtained in this work, allow infer that some useful qualitative information can be extracted from this method analysis approach.
The main information outlined from this comparison is that:
1) The graded cumulative length map can be used to have information on located deeper structures and/or bodies as those provided by the geoid map from [41];
2) The LFD map give a good representation of the shallower (Moho + 10 km in this study) lithospheric structuration.
5. Conclusions
This study focused on the analysis of the spatial distribution of mapped lineaments in equatorial Africa. The analysis for mapped lineaments was carried out, by using some (graphical, analytical) software, and the results are displayed as raw and graded maps. The comparison of those maps with geophysical data highlights the rela-
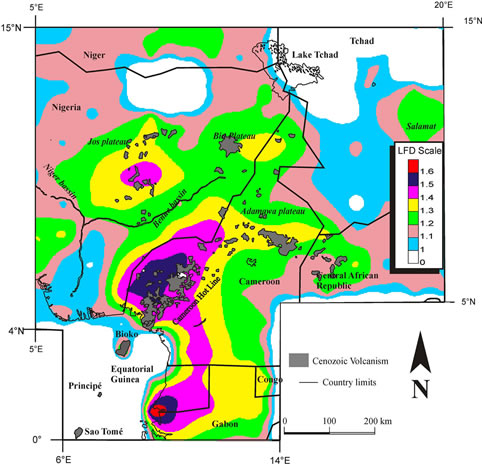
Figure 7. Intensity map of spatial distribution of the LFD represented as curves of iso-values, on a simplified (recent Cainozoic volcanism) map.
tionship between complexity of spatial distribution of lineaments and lithosphere structure in equatorial Africa.
According [9] work, high LFD values are in the most recent tectonic and volcanic active areas (CHL), where fracture network is supposed to be more evolved (high fractal values), whereas in areas with less intense or absent tectonic active, the old basement, show remnants of old deformation events. The recent tectonic and volcanic activity developed in the weakest portion of the lithosphere in the studied area.
As the geoid is a complementary source of information about the earth’s (planets) internal structure, and in areas where geological information are not abundant, the complexity in the spatial distribution of the lineaments can give the same information in a qualitative way. This approach can provide a bridge between classical geology and geophysics, and particularly powerful for studying large and inaccessible regions. The approach proposed is thus very effective in gathering basic information for exploration geology in remote areas on Earth and for investigations in planets.
6. Acknowledgements
The author wishes to thank Prof. P. Gaspard who has
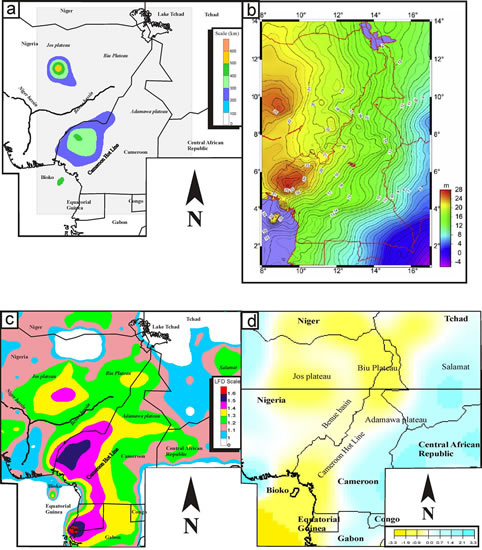
Figure 8. Representation from the comparison between the results obtained from the analysis of lineaments in equatorial Africa, with some geophysical data from the same region. a) Graded map of spatial distribution of the cumulate length (same legend as in Figure 5); b) Geoid map of Cameroon and part of the adjacent countries, contoured at 0.5 m intervals after Kamguia et al 2008; c) Graded map of spatial distribution of the LFD represented as curves of iso-values (legend as in Figure 7); d) Diffraction tomography map (variations of S-wave velocity at a depth of Moho + 10 km, speed reference here is 4589 km/s) obtained by Shapiro and Ritzwoller (2002). Different colors represent the speed variation of the refraction of seismic waves which also corresponds to the relative differences of the temperature, and the lithospheric thickness between the areas. The transition from yellow to blue corresponds to the decrease in speed (m/s) of the waves, in temperature and the increase of lithospheric thickness. Simplified graded LFD density map was superposed on the tomography map.
discussed the many aspects of this work. This work was financially supported by a grant from the “Fondation Van Buuren” (ULB).
REFERENCES
- N. Kellgren, “Applicability of Remote Sensing Techniques to Groundwater Exploration in Semi-Arid Hard Rock Terrain,” Ph.D. Dissertation, Chalmers University of Technology, Göteberg, 2002, p. 110.
- T. C. Ekneligoda and H. Henkel, “The Spacing Calculator Software—A Visual Basic Program to Calculate the Spatial Properties of Lineaments,” Computers and Geosciences, Vol. 32, No. 4, 2006, pp. 542-553. doi:10.1016/j.cageo.2005.08.007
- T. C. Ekneligoda and H. Henkel, “Interactive Spatial Analysis of Lineaments,” Computers and Geosciences, Vol. 36, No. 2, 2010, pp. 1081-1090. doi:10.1016/j.cageo.2010.01.009
- C. Nkono, “Multi-Scale Analysis and Geodynamic InterPretation of the Morphostructurales Data Associated from the Phanerozoic Volcano-Plutonism Activity of Equatorial Africa (Cameroon Line and Neighbouring Regions),” Thesis, Université Libre de Bruxelles (ULB), Bruxelles, 2008, p. 356.
- C. Nkono, O. Féménias and D. Demaiffe, “Geodynamic Framework of Large Volcanic Fields Highlighted by SRTM DEMs: Method Evaluation and Perspectives Exampled on Three Areas from the Cameroon Volcanic Line,” Journal of Volcanology and Geothermal Research, Vol. 187, No. 1-2, 2009, pp. 13-25. doi:10.1016/j.jvolgeores.2009.06.007
- D. Unwin, “Fractals and the Geosciences: Introduction,” Computers & Geosciences, Vol. 15, No. 2, 1989, pp. 163-165. doi:10.1016/0098-3004(89)90031-9
- P. A. Burroughs, “Fractals and Geochemistry,” In: D. Avnir, Ed., The Fractal Approach to Heterogeneous Chemistry, Wiley, New York, 1989, pp. 383-406.
- M. Vignes-Adler, A. Le Page and P. M. Adler, “Fractal Analysis of Fracturing in Two African Regions, from Satellite Imagery to Ground Scale,” Tectonophysics, Vol. 196, No. 1-2, 1991, pp. 69-86. doi:10.1016/0040-1951(91)90290-9
- C. C. Barton, “Fractal Analysis of Scaling and Spatial Clustering of Fractures,” In: C. C. Barton and P. R. La Pointe, Eds., Fractals in the Earth Sciences, Plenum Press, New York, 1995, pp. 141-178. doi:10.1007/978-1-4899-1397-5_8
- D. L. Turcotte, “Fractal Model for Crustal Deformation,” Tectonophysics, Vol. 132, No. 1-3, 1986, pp. 261-269. doi:10.1016/0040-1951(86)90036-3
- D. L. Turcotte, “A fractal Approaches to Probabilistic Seismic Hazard Assessment,” Tectonophysics, Vol. 167, No. 2-4, 1989, pp. 171-177. doi:10.1016/0040-1951(89)90067-X
- D. L. Turcotte, “Fractals and Chaos in Geology and Geophysics,” Cambridge University Press, Cambridge, 1992, p. 398.
- B. B. Mandelbrot, “The Fractal Geometry of Nature,” W.H. Freeman and Company, New York, 1982, p. 468.
- W. J. Morgan, “Hotspot Tracks and the Early Rifting of the Atlantic,” Tectonophysics, Vol. 94, No. 1-4, 1983, pp. 123-139. doi:10.1016/0040-1951(83)90013-6
- S. J. Freeth, “Tectonic Activity in West-Africa and Gulf of Guinea since Jurassic Times—Explanation Based on Membrane Tectonics,” Earth and Planetary Science Letters, Vol. 38, No. 2, 1978, pp. 298-300. doi:10.1016/0012-821X(78)90103-6
- J. G. Fitton, “The Benue through and Cameroon Line—A Migrating Rift System in West-Africa,” Earth and Planetary Science Letters, Vol. 51, No. 1, 1980, pp. 132-138. doi:10.1016/0012-821X(80)90261-7
- J. G. Fitton and H. M. Dunlop, “The Cameroon Line, West-Africa, and Its Bearing on the Origin of Oceanic and Continental Alkali Basalt,” Earth and Planetary Science Letters, Vol. 72, No. 1, 1985, pp. 23-38. doi:10.1016/0012-821X(85)90114-1
- C. Moreau, J.-M. Regnoult, B. Deruelle and B. Robineau, “A New Tectonic Model for the Cameroon Line, CentralAfrica,” Tectonophysics, Vol. 141, No. 4, 1987, pp. 317-334.
- B. Déruelle, C. Moreau, C. Nkoumbou, R. Kambou, J. Lissom, E. Njongfang, R. T. Ghogomu and A. Nono, “The Cameroon Line: A Review,” In: A. B. Kampunzu and R. T. Lubala, Eds., Magmatism in Extensional Structural Settings the Phanerozoic African Plate, SpringerVerlag, Berlin, 1991, pp. 274-327. doi:10.1007/978-3-642-73966-8_12
- D. C. Lee, A. N. Halliday, J. G. Fitton and G. Poli, “Isotopic Variations with Distance and Time in the Volcanic Islands of the Cameroon Line—Evidence for a Mantle Plume Origin,” Earth and Planetary Science Letters, Vol. 123, No. 1-3, 1994, pp. 119-138. doi:10.1016/0012-821X(94)90262-3
- J. B. Meyers, B. R. Rosendahl, C. G. A. Harrison and Z. D. Ding, “Deep-Imaging Seismic and Gravity Results from the Offshore Cameroon Volcanic Line, and Speculation of African Hotline,” Tectonophysics, Vol. 284, No. 1-2, 1998, pp. 31-63. doi:10.1016/S0040-1951(97)00173-X
- R. Montigny, I. Ngounouno and B. Déruelle, “Âges K-Ar des Roches Magmatiques du fossé de Garoua (Cameroun): Leur Place Dans le Cadre de la ‘Ligne du Cameroun’,” Comptes Rendus Geoscience, Vol. 336, No. 16, 2004, pp. 1463-1471. doi:10.1016/j.crte.2004.08.005
- B. Déruelle, I. Ngounouno and D. Demaiffe, “The ‘Cameroon Hot Line’: A Unique Example of Active Alkaline Intraplate Structure in both Oceanic and Continental Lithosphere,” Comptes Rendus Geoscience, Vol. 339, No. 9, 2007, pp. 589-600. doi:10.1016/j.crte.2007.07.007
- K. Rankenburg, J. C. Lassiter and G. Brey, “Origin of Megacrysts in Volcanic Rocks of the Cameroon Volcanic Chain—Constraints on Magma Genesis and Crustal Contamination,” Contributions to Mineralogy and Petrology, Vol. 147, No. 2, 2004, pp. 129-144. doi:10.1007/s00410-003-0534-2
- D. C. Turner, “Volcanoes of the Biu Basalt Plateau, Northeastern Nigeria,” Journal of Mining and Geology, Vol. 15, No. 2, 1978, pp. 49-63.
- M. A. Olade, “Evolution of Nigeria’s Benue Trough (Aulocogen): A Tectonic Model,” Geological Magazine, Vol. 112, No. 6, 1975, pp. 575-581. doi:10.1017/S001675680003898X
- J. Benkhelil, “The Origin and Evolution of the Cretaceous Benue Trough (Nigeria),” Journal of African Earth Sciences, Vol. 8, No. 2-4, 1989, pp. 251-282. doi:10.1016/S0899-5362(89)80028-4
- J. Benkhelil, “Benue Trough and Benue Chain,” Geological Magazine, Vol. 119, No. 2, 1982, pp. 155-168. doi:10.1017/S001675680002584X
- J. Penaye, S. F. Toteu, R. Tchameni, W. R. Van Schmus, J. Tchakounte, A. Ganwa, D. Miyem and E. N. Nsifa, “The 2.1 Ga West Central African Belt in Cameroon: Extension and Evolution,” Journal of African Earth Sciences, Vol. 39, No. 3-5, 2004, pp. 159-164. doi:10.1016/j.jafrearsci.2004.07.053
- J.P. Prian, B. Coste, J. Eko Ndong, V. Johan and P. Ledru, “Geological and Geochemical Synthesis, Potentialities Mining of Boué Degree Square (Central Gabon) with Geological Map 1/200,000, Gabonese Republic,” Ministry of Mines and Hydrocarbons, Libreville; BRGM, Orléans, 1990, p. 103.
- R. J. Thomas, J. F. Makanga and L. Chevallier, “Geological Map of the Gabonese Republic to the 1/1000.000 with Explanatory Notes,”Ministry of Mines, Oil and Water Resources, Libreville, 2002, p. 195.
- A. Nédélec, D. Minyem, P. Barbey, “High-P—High-T Anatexis of Archean Tonalitic Grey Gneisses: The Esèka Migmatites, Cameroon,” Precambrian Research, Vol. 62, No. 3, 1993, pp. 191-205. doi:10.1016/0301-9268(93)90021-S
- S. F. Toteu, W. R. Van Schmus, J. Penaye and J. B. Nyobe, “U-Pb and Sm-Nd Evidence for Eburnean and Panafrican High-Grade Metamorphism in Cratonic Rocks of Southern Cameroon,” Precambrian Research, Vol. 67, No. 3-4, 1994, pp. 321-347. doi:10.1016/0301-9268(94)90014-0
- P. Launeau, “Evidence of Magmatic Flow by 2-D Image Analysis of 3-D Shape Preferred Orientation Distributions,”Bulletin de la Société Géologique de France, Vol. 175, No. 4, 2004, pp. 331-350. doi:10.2113/175.4.331
- P. Launeau and P.-Y. Robin, “Fabric Analysis Using the Intercept Method,” Tectonophysics, Vol. 267, No. 1-4, 1996, pp. 91-119. doi:10.1016/S0040-1951(96)00091-1
- P. Launeau and A. R. Cruden, “Magmatic Fabric Acquisition Mechanism in a Syenite: Results of a Combined Anisotropy of Magnetic Susceptibility and Image Analysis,” Journal of Geophysical Research: Solid Earth (1978-2012), Vol. 103, No. B3, 1998, pp. 5067-5089. doi:10.1029/97JB02670
- C. Tarnier, G. Vuidel and P. Frankhauser, “Delimitation of Morphological Datasets by a Multi-Scale Approach, Application to the Morphological Delimitation of Agglomerations,”8th Meeting de Théo Quant, Besançon, 2008, p. 14.
- C. Tarnier, G. Vuidel, P. Frankhauser and H. Houot, “An Urban Multi-Scale Simulation Tool Using Fuzzy Evaluation of Accessibility and Morphological Constraints,” 48th Congress of the European Regional Science Association, Liverpool, 2008.
- P. Frankhauser, C. Tarnier, G. Vuidel and H. Houot, “Fractal Approach to Urbanization, Analytical Methods of Accessibility and Multi-Scale Simulations,” 11th World Conference on Transportation Research, Geography, Berkeley, 2007, p. 21.
- P. Frankhauser, C. Tarnier, G. Vuidel and H. Houot, “A Multi-Scale Approach of Accessibility to Control Urban Sprawl,” TUM2008 in Munich, 2008, p. 19.
- J. Kamguia, R. Nouayou, C. T. Tabod, J. M. Tadjou, E. Manguelle-Dicoum and H. L. Kande, “Geophysical Signature of Geological Units Inferred from the Analysis of Geoid Maps in Cameroon and Its Surroundings,” Journal of African Earth Sciences, Vol. 52, No. 1-2, 2008, pp. 1-8. doi:10.1016/j.jafrearsci.2008.02.002
- N. Shapiro and M. Ritzwoller, “Monte-Carlo Inversion for a Global Shear-Velocity Model of the Crust and Upper Mantle,” Geophysical Journal International, Vol. 151, No. 1, 2002, pp. 88-105. doi:10.1046/j.1365-246X.2002.01742.x
NOTES
*Corresponding author.

