Open Journal of Discrete Mathematics
Vol.06 No.03(2016), Article ID:67516,52 pages
10.4236/ojdm.2016.63012
On the Erdős Distance Conjecture in Geometry
Amir Jafari, Amin Najafi Amin
Department of Mathematics, Sharif University of Technology, Tehran, Iran

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 8 March 2016; accepted 18 June 2016; published 21 June 2016
ABSTRACT
Erdős asks if it is possible to have n points in general position in the plane (no three on a line or four on a circle) such that for every i (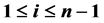 ) there is a distance determined by the points that occur exactly i times. So far some examples have been discovered for
) there is a distance determined by the points that occur exactly i times. So far some examples have been discovered for 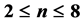 [1] [2] . A solution for the 8 point is provided by I. Palasti [3] . Here two other possible solutions for the 8 point case as well as all possible answers to 4 - 7 point cases are provided and finally a brief discussion on the generalization of the problem to higher dimensions is given.
[1] [2] . A solution for the 8 point is provided by I. Palasti [3] . Here two other possible solutions for the 8 point case as well as all possible answers to 4 - 7 point cases are provided and finally a brief discussion on the generalization of the problem to higher dimensions is given.
Keywords:
Erdős Distance Problem, General Position, Graph Pattern, Distance Distribution

1. Introduction
It seems certain that if n is large enough the Erdős problem mentioned above has no solution [1] , but Erdős offers $50 for a proof (and $500 for examples with n arbitrarily large). So far, examples have been discovered for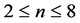 . These are due to Pomerance (5), Andy Liu and several Hungarian students (6), and I. Palasti (7, 8) [1] [3] - [5] . The remaining questions are as follows:
. These are due to Pomerance (5), Andy Liu and several Hungarian students (6), and I. Palasti (7, 8) [1] [3] - [5] . The remaining questions are as follows:
1) Is there an example for n = 9 or no such examples exists? [1]
2) How many independent patterns are there for 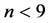 in the plane?
in the plane?
3) Is it possible to have n arbitrarily large for the same problem in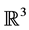 , or indeed in
, or indeed in 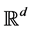 for any
for any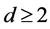 ?
?
The aim of this article is to analyze the second question and give a brief discussion about the third question. Indeed all possible solutions for 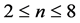 will be introduced in this text and for n = 9 some examples will be presented that are very close to the intended solution. Accordingly, first the easier 4 point-2D cases are discussed and then 5, 6, 7 and 8 point cases are presented and finally a brief discussion of higher dimensions will be provided. The general position condition prevents obvious symmetries. Without this condition, the problem has trivial solutions for any number of points. Since by adding additional number of points, the number of equations is increased faster than the number of free variables, to find the resulting algebraic equations’ system, a different type of symmetry is required. For example, for 2D cases, if the number of points is more than 5, the number of free variables will be less than the number of equations. There are 14 free variables in 9 point case while 28 quadratic equations must be solved simultaneously. By increasing the number of points, equilateral and isosceles triangles and parallelogram will appear in the figures.
will be introduced in this text and for n = 9 some examples will be presented that are very close to the intended solution. Accordingly, first the easier 4 point-2D cases are discussed and then 5, 6, 7 and 8 point cases are presented and finally a brief discussion of higher dimensions will be provided. The general position condition prevents obvious symmetries. Without this condition, the problem has trivial solutions for any number of points. Since by adding additional number of points, the number of equations is increased faster than the number of free variables, to find the resulting algebraic equations’ system, a different type of symmetry is required. For example, for 2D cases, if the number of points is more than 5, the number of free variables will be less than the number of equations. There are 14 free variables in 9 point case while 28 quadratic equations must be solved simultaneously. By increasing the number of points, equilateral and isosceles triangles and parallelogram will appear in the figures.
2. Problem in 2D Case
Let 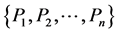 be n point in the plane corresponding to a solution of Erdős problem, where
be n point in the plane corresponding to a solution of Erdős problem, where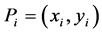 . And suppose that n − 1 distinct distances produced by these points are:
. And suppose that n − 1 distinct distances produced by these points are: 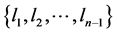 so that the length li repeats i times and the distance between the points
so that the length li repeats i times and the distance between the points 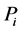 and
and 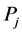 are presented as
are presented as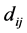 . Without loss of generality, we can choose
. Without loss of generality, we can choose 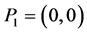 and
and 




will be algebraic numbers. It is possible to consider a graph pattern for each solution so that the weight of the edges of the graph corresponds to the number of relevant repeated lengths appeared in the geometric solution of the problem which is a number between 1 to n.
2.1. 4 Point Patterns
The solution of the 2 point case is single line and in 3 point case it is an isosceles triangle which is not an equilateral triangle. For 4 point case, the following 5 solutions are available that the last two solutions have a unique graph pattern in Figure 1 where the edges with the same color are equal. In all above cases, it is possible to consider 


In order to generalize the problem, if the sequence of distinct lengths which is the set 
The sequences listed above for 4 point case, have one free variable. Other possible cases for the 4 point problem include sequences {1,1,1,3} and {1,1,2,2} that have two degrees of freedom (two free variables) and the sequences {1,5}, {2,4} and {3,3} the degree of freedom of which is zero and in this case we have four fix points:
Table 1. 4 point solutions of sequence {1,2,3}.
Note: For four point cases, we have maximum 4 degrees of freedom, but in this problem, we only need to discuss about zero, one and two degrees of freedom cases. To find the solution to the main problem for more than 4 points a computational algorithm is required which is discussed below.
Method 1: Suppose that the points 




1) All intersection points of perpendicular bisectors of the sides related to two entrees of points 
2) All intersection points of the circles with radius 


3) All intersection points of the circles with radius 




Note: The main problem is to review various patterns of length sequence









Our general strategy to solve Erdős problem is to start with a previously known example, i.e. 4 point or 5 point case and add new points using method 1. If this method fails we want to show that adding one new point with free variable coordinates will enable us complete this strategy by using method 1. Suppose we constricted b points in the plane with d distinct distances given by 

Because in other cases, this new point can be found using method 1. Note that 

It is obvious that at each step of adding new point, if we have:
Number of existing points > 
then we can obtain all remain points only by using method 1. The maximum number of new points added by the above process is called 
We want to start with b = 4 points. For 4 point pattern with m free variables, we have






2.2. 5 Point Patterns
Regardless of the dimension, a total of 118 independent weighted graphs are considered for the 5 point case. These 118 cases can be classified based on six general cases to have four equal lengths in this graph. To find all the possible 5 point patterns, it is necessary to analyze the equation system of 118 independent graphs. In 2D case some of these cases may either not lead to a solution or lead to more than one solution. The following Table 2 presents the 6 cases of 4 point state along with independent graphs of each state and the number of solutions found in 2D case.
After solving the equations a total of 89 five point patterns are obtained that other than the first example given below, which has one degree of freedom, for the rest of 88 solutions 5 fixed points are obtained. But there is another way to analyze all possible scenarios of five point case which is using method 1 because if there is a five point pattern with a sequence of lengths

Table 2. The number of solutions of 5 point in 2D case, for each 4 point state, based on the graph patterns.
Figure 1. 4 point solutions of sequence {1,2,3}.
Figure 2. Solutions of 4 point with {1,1,4} and {2,2,2} sequences.
Our first pattern with one degree of freedom for 5 points that can produce six, seven and eight point patterns is called pattern (*) and is as Figure 3.





value other than 0 and −75 degree within the range of −150 < a < 30. The coordinates of 
and the coordinates of the other two points in terms of a are:

Also, we have the following angle relations:

All 89 five point 2D solutions are presented in Table 3, all of which apart from numbers 42 and 43 can be obtained by 4 point pattern of sequence {1,2,3}, i.e. there is a vertex whose removal leads to one of the 4 point solutions with the sequence of lengths {1,2,3}.
2.3. 6 Point Patterns
First we show that all 6 point cases any sequence lengths 


The rule is proved by removing the marked vertex in the above figure. Otherwise, the graph is as follows:
So then one of the following cases is true that either two vertices are removed that are presented in the figure:


Or there will be the following case:
The last case requires a little more analysis. If four edges with the weights 4 are connected to vertices a and f, the solution is presented by the same vertices, otherwise there are at least 3 edges with the weights of 5 among the edges
Otherwise, there must be at least two edges with a weight of 4 among the edges 

Now, using method 1 and also four and five point patterns it is possible to search for 6 point patterns. 54 solutions are obtained in this way 47 of which are obtained by adding one point to the 5 point patterns and only 7 solutions are obtained by adding two points to the 4 point patterns. But we guess that, there must be 55 solutions in this case based on the probable relation between the number of solutions and Fibonacci numbers which this issue has been more explained in section 2.7.
Figure 3. Pattern (*).
Table 3. 5 point solutions of sequence {1,2,3,4}.
Seven patterns obtained by pattern (*) are presented:
1) In the three first patterns the value of angle can be selected as a free variable. Since the first 5 points are the same as pattern (*), only the coordinates of the new point 
2) The next four results are related to two specific angles a discussed in the following Table 5.
The 40 remaining solutions are presented in the following Table 6. The index of column j presents the 5 point pattern of the previous stage that the solution of the 6 point case is obtained by adding a single point to it:
The six cases that are not directly obtained by 5 point cases but they are obtained by adding two new points to four point patterns are presented in Table 7.
Pattern 48 in the above table, was presented by I. Palasti in 1989 [4] .
2.4. 7 Point Patterns
In 7-point case, in addition to the 4 point sequences of one degree of freedom, the 4 point sequences of two degrees of freedom will be required i.e. the sequences {1,1,1,3} and {1,1,2,2}. Obviously it is always possible to remove the vertices connected to the edges with the weight of 1, 2 and 2 that accordingly a maximum of 3 vertices will be removed and there will be 4, 5 and 6 point pattern with a maximum of 4 distinct lengths. Of course, in 5 and 6 point cases it is possible to remove two other vertices so that the maximum remaining lengths are 4 distinct lengths. Therefore it is just needed to analyze 4 point case with a maximum of 4 distinct lengths.
Table 4. 6 point solutions obtained from pattern (*) with one degree of freedom.
Table 5. 6 point solutions obtained from pattern (*) with fix coordinates.
Then using method 1 and also 4, 5 and 6 point patterns, it is possible to search for 7 point patterns. 13 solutions are obtained in this way 9 of which are obtained by adding a new point to the 6 point patterns and two solutions are obtained by adding two new points to the 5 point pattern (*) and two of them are obtained by adding three points to 4 point patterns. Among all solutions only the first solution has the free variable a and in the rest of solutions all points are fixed and non parametric. The coordinates of the points 

And also we have:
The above solution is obtained by the reunion of patterns 1 and 2 in Table 4 both of which were obtained by a five point pattern (*) (Figure 4).
The remaining 8 solutions extracted from 6 point patterns are presented in the following Table 8 in which column j presents the number of the pattern or the related 6 point productive patterns:
Pattern 9 in the above table, was presented by Andy Liu in 1987 [5] but all of the other patterns are new. The other two solutions obtained by 5 point solution (*) are as follows (Table 9):
And at the end of this section two solutions of 4 point pattern obtained by adding three new points are as follows Table 10.
Pattern 13 in the above table, was presented by I. Palasti in 1989 [3] .
2.5. 8 Point Patterns
In the eight point case we have to show that it is always possible to obtain a 4 point pattern by removing 4 vertices with maximum 4 distinct lengths that can be one of the length sequences of {1,2,3}, {2,2,2}, {1,1,4}, {1,1,1,3} or {1,1,2,2}. We know that there are 6 edges with the weights of 1 - 3. Thus there is a graph with 6 edges and 8 vertices. Therefore at least one of the vertices is connected to two edges, by removing this edge, we
Table 6. 6 point solutions obtained from 5 point solutions.
will obtain a graph with 7 vertices and 4 edges. Thus in this case there is at least one vertex that is connected to two edges. By removing this vertex two other edges will be removed. Then two edges are remained that it is possible to remove these two edges by removing two other vertices. So we will get a graph with 4 vertices that had a maximum of four distinct lengths. The problem in 8 point case has two other solutions other than the solution discussed at the beginning both of which are directly obtained by the pattern 1 in 7-point case by adding a new point that all three solutions are presented in Table 11. The first solution belongs to I. Palasti in [3] .
Closely related to the length sequence {1,2,3,4,5,6,7} there are 5 other examples with one degree of freedom. The sequence of distinct lengths of two initial solutions is {1,1,2,2,4,5,6,7} and these two solutions are presented in Table 12. The sequence of distinct lengths of the next three solutions is {1,1,1,3,4,5,6,7} which are presented in Table 13.
2.6. 9 Point Patterns
Using the discussed method no pattern was obtained for 9 point case, however this does not guarantee that there will be no solution for 9 point case. Here some solutions are presented that are very close to the intended solution and in fact they were the solutions that only needed one additional condition to be a candidate for the main solution. The initially expressed solutions have one free variable. The following solution is the only one that is not obtained by 5 point (*) pattern. This pattern still has the free variable a and its distinct length sequence includes {1,2,2,3,4,5,6,6,7}. Although there is a free variable and only one other equation is required that can be any of the following equations that are related to the equations with the repetitions of 2 and 6:



The following cases that are obtained by five point pattern (*) they still have the free variable a. The sequence of distinct lengths of the first two solutions is {1,2,3,3,3,4,5,7,8} and in case of the other two solutions this sequence includes {1,1,2,2,4,5,6,7,8} (Table 15).
All solutions that are presented below have fixed points and they have no free variable. First the solutions with independent lengths of {1,1,2,2,4,5,6,7,8} (Table 16).
And solution of sequence {1,1,2,3,3,5,6,7,8} (Table 17).
And the last solution close to the original answer to the problem by distinct lengths {1,1,1,3,4,5,6,7,8} is as follows (Table 18).
2.7. Conclusion for 2D Case
Based on the results presented in the previous sections it can be observed that in 2D case the number of n point solutions for the value of n between 1 and 8, it is based on Fibonacci sequence [6] . The Fibonacci sequence is as follows: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, …
On the other hand (Table 19).
Therefore, the solutions can be presented in the following chart where the horizontal axis represents the number of points, and the vertical axis presents the Fibonacci number index corresponding to the number of points (Figure 5).
Table 7. 6 point solutions obtained from 4 point solutions.
Table 8. 7 point solutions obtained from 6 point solutions.
Table 9. 7 point solutions obtained from 5 point solutions.
Table 10. 7 point solutions obtained from 4 point solutions.
Figure 4. 7 point solution obtained from pattern (*) with one degree of freedom.
Figure 5. Relation between the number of solutions for 1-8 point cases and index of Fibonacci numbers.
Table 11. 8 point solutions for length sequence {1,2,3,4,5,6,7}.
Note: In the above table we have
We do not know why Fibonacci number appears in the above table and an explanation of this fact seems to be very interesting.
3. Generalization to Higher Dimensions
When the number of dimensions increases the dimension of the solutions is increased as well but the seemingly independent solutions are united together. For example, in cases where two distinct solutions were obtained from the intersection of two circles on the 2D plane, this solution will be the result of the intersection of two spheres which is a circle in 3D space. Thus, two distinct points that produce two distinct solutions in two dimensional cases give way to the same solution with a higher dimension.
Therefore, by increasing the number of dimensions, it is just enough to consider the graph pattern cases to find the n-point independent solutions, so the limited sequence of number of solutions can be obtained, only by counting the number of graph patterns.
For example the 4 point state that only has 4 independent cases can be easily analyzed. The 4 point case solution was presented for a desired number of dimensions greater than 2 in table 1. By increasing the number of dimensions, the number of solutions remains 4 but the dimension of the solutions increases at each stage. Also as mentioned in section 2-1 the number of independent 5 point cases graph patterns was 118 cases.
3.1. Analyzing 5 Point Case in 3D Space
To determine the number of independent solutions of 5 point 3D case it should be noted that one can always fix 4 points with arbitrary pattern of a sequence related to distinct lengths. Thus, only the fifth point should be found. If there is a vertex the attached sides of which are 



Table 12. Solutions of sequence {1,1,2,2,4,5,6,7} with one degree of freedom.
Table 13. Solutions of sequence {1,1,1,3,4,5,6,7} with one degree of freedom.
Table 14. Solution of sequence {1,2,2,3,4,5,6,6,7}.
Table 15. Solutions of sequence of {1,2,3,3,4,5,7,8} & {1,1,2,2,4,5,6,7,8}.
Table 16. Solutions of sequence {1,1,2,2,4,5,6,7,8}.
Table 17. Solutions of sequence {1,1,2,3,3,5,6,7,8}.
Table 18. Solution of sequence {1,1,1,3,4,5,6,7,8}.
Table 19. Number of independent solutions for 1 - 8 points.
cases for
So, the sequence of the number of solutions in 3D case is:
On the other hand the (1,3)-Fibonacci sequence is [7] :
So, based on all above discussions, we ask is there any relation between the number of solutions of the sequence length of 
Cite this paper
Amir Jafari,Amin Najafi Amin, (2016) On the ErdÖs Distance Conjecture in Geometry. Open Journal of Discrete Mathematics,06,109-160. doi: 10.4236/ojdm.2016.63012
References
- 1. Croft, H.T., Falconer, K.J. and Guy, R.K. (2012) Unsolved Problems in Geometry. Springer Science & Business Media, Berlin.
- 2. ErdÖs, P. (1986) On Some Metric and Combinatorial Geometric Problems. Discrete Mathematics, 60, 147-153. http://dx.doi.org/10.1016/0012-365X(86)90009-9
- 3. Palasti, I. (1989) Lattice-Point Examples for a Question of ErdÖs. Periodica Mathematica Hungarica, 20, 231-235. http://dx.doi.org/10.1007/BF01848126
- 4. Palasti, I. (1989) A Distance Problem of P. ErdÖs with Some future Restrictions, North-Holland. Discrete Mathematics, 76, 155-156. http://dx.doi.org/10.1016/0012-365X(89)90309-9
- 5. Liu, A. (1987) On the “Seven Points Problem” of P. ErdÖs. Studia Scientiarum Mathematicarum Hungarica, 22, 447-448.
- 6. Beck, M. and Geoghegan, R. (2010) The Art of Proof: Basic Training for Deeper Mathematics. Springer, New York.
- 7. Lee, G.Y. and Asci, M. (2012) Some Properties of the (p,q)-Fibonacci and (p,q)-Lucas Polynomials. Journal of Applied Mathematics, 2012, Article ID: 264842.






































