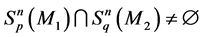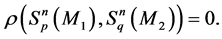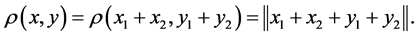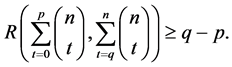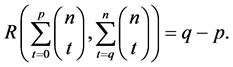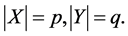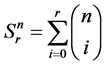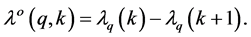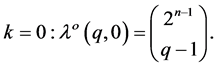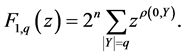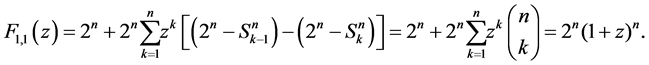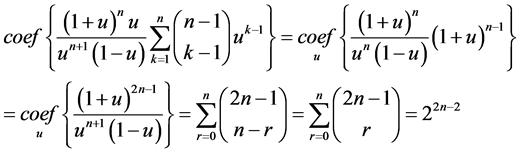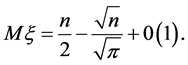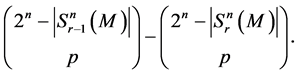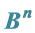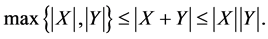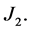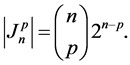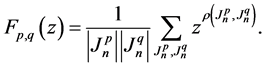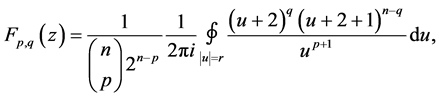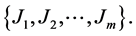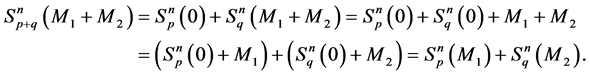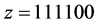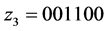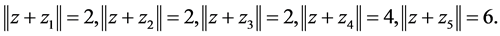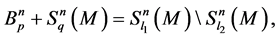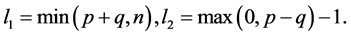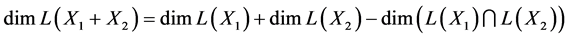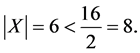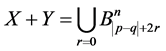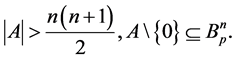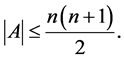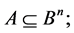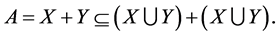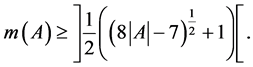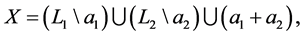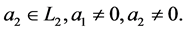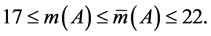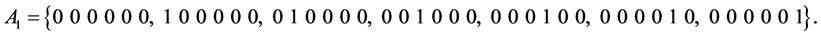Open Journal of Discrete Mathematics
Vol.06 No.02(2016), Article ID:65251,16 pages
10.4236/ojdm.2016.62004
Algebra and Geometry of Sets in Boolean Space
Vladimir Leontiev1, Garib Movsisyan2, Zhirayr Margaryan3
1Moscow State University, Moscow, Russia
2BIT Group, Moscow, Russia
3Yerevan State University, Yerevan, Armenia

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 16 October 2015; accepted 28 March 2016; published 31 March 2016
ABSTRACT
In the present paper, geometry of the Boolean space Bn in terms of Hausdorff distances between subsets and subset sums is investigated. The main results are the algebraic and analytical expressions for representing of classical figures in Bn and the functions of distances between them. In particular, equations in sets are considered and their interpretations in combinatory terms are given.
Keywords:
Equations on Sets, Hausdorff Distance, Hamming Distance, Generating Function, Minkowski Sum, Sum of Sets

1. Distance between Subsets Bn
Let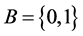 ,
, 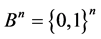 and
and 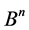 be the set of all words of finite length in the alphabet B. For
be the set of all words of finite length in the alphabet B. For 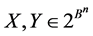 we take:
we take:
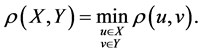
It is clear that 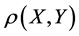 is the Hausdorff distance between the subsets
is the Hausdorff distance between the subsets 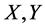 and
and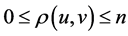 , and
, and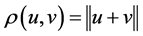 is the Hamming distance between the points:
is the Hamming distance between the points: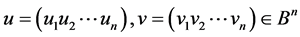 , where
, where 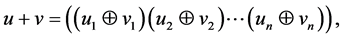 and
and 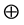 is the addition operation with respect to mod 2.
is the addition operation with respect to mod 2.
The Hausdorff distance has essential role in many problems of discrete analysis [1] and thus has certain interest. On the other hand, there only are a few essential results concerning distances between the subsets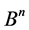 , and their investigation offers significant difficulties.
, and their investigation offers significant difficulties.
First, we present the following simple properties of the Hausdorff distance:
1)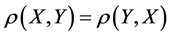 ;
;
2)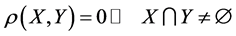 ;
;
3) Если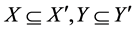

4)
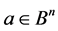
Let us note that, generally speaking, the Hausdorff distance does not satisfy the triangle inequality:

which is demonstrated in the following picture:
But inequality (1) holds true if
Distance between Spheres in Bn
Let 
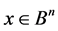
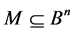
Thus, we have the following two equvalent interpretations for
1) 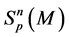

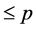
2) 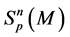
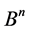
Examples.
1)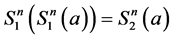
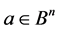
2)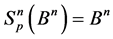
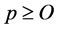
3) If 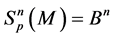

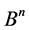
Theorem 1.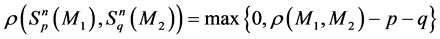
Proof. We consider two cases.
a) 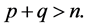
and, consequently,
b) 

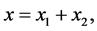

From here we have:
As 
Then, taking into account that:

we have:
The theorem is proved.
Let:
Taking into account that the sphere of the radius p with the center at 

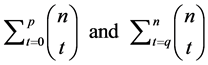
we get the following corollary.
Corrollary. If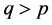
The value of the function 
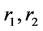
Theorem 2. If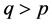
The general form of the standard generating function for the distance between the subsets 
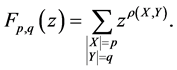
The summation in (2) is over all pairs of the subsets 
Let us consider a few examples.
1)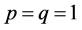
In this case, we have:
Thus, 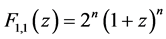
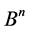
2)
In this case:
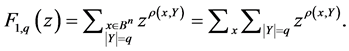
As:
for arbitrary points 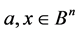
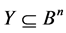
Then:
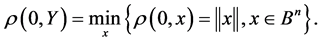
Consequently, the distance between the zero point and an arbitrary subset Y equals the minimal weight of the points which are in Y.
Hence, 
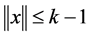

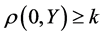
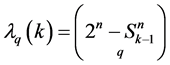
where
where 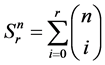
From (5), we get the following statement:
Lemma1. If 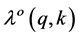
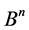
For
Theorem 3. The following formula holds true:

Proof. By definition:
From this and Lemma 1, taking into account (3) and (4), we get:
The theorem is proved.
If 



Corollary 1. The following formula holds true:
Corollary 2. The following holds true:
Corollary 3. The formula for 
Proof. From (6) we get for p = 1:
Corollary 4. For q = 2, the following formula holds true:
Proof. By definition and from Corollary 2, we derive:
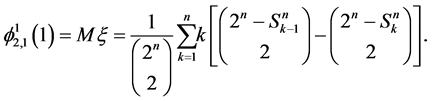
Transforming the terms in (7), we get:

Then, using the following formulas:
Let us “compress” the sum:
By definition, we have:
Furthermore, if:
then:
Further:
And:
From here it follows that
Then:
Taking this and (8) into account, we get:
And the generating function:
can be expressed by the following parameters:
2) if 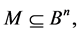





Hence, the set 
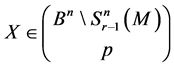

The cardinality of this family is:

2) The number of all m-element subsets having the distance r from M is:
Summarizing all the previous, we get the following statement.
Theorem 4. The following expression is true:
2. Sum of Sets in
Let
The operation “+” is defined in the family 



Besides, the following inequality holds true:
Here both limits are reachable.
The properties of “+” are as follows:
1)
2) 

3) 
4) 
5) 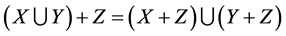
6)
7)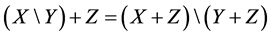
Examples.
If X is a subspace in
1)
2) 
Let the following holds true:

Then
Thus, there is certain analogy between the norm of the sum of points and the distance between those points, as well as between the norm of the sum of the sets and the distance between those sets.
In the general form, the following statement connecting the operations “∪” и+, is true:
2.1. Sum of Facets in Bn and the Distance between Them
A facet or interval in 



Every interval J can be written in the form of a word of the length n, in the alphabet 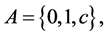
Examples.
If 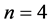
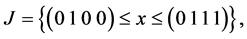

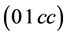


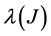


If the operation “*” is introduced on the alphabet A:
then the sum 

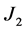

Examples.
1) If 

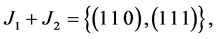
2) If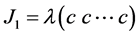

The distance between the intervals 


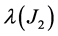
Let 
Statement 1.
Thus, the distance between the intervals 
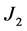
Examples.
1) Let
Then 
Let 

Let us consider the direct product 
Theorem 5. The following formula is true:
where
Let us consider the matrix 

Lemma 2. The following expression is true:
where 
Proof. According to the definition:

where
and 
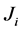
It follows from (9):

The internal sum in (10) equals the number of such pairs 
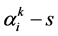

Example.
1) Let 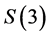

The total number of the edges in 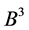

all letters of the alphabet 

From here, we get:
2) In the general form, if 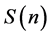
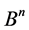
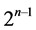
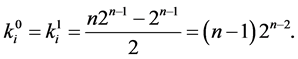

Thus, the sum of the pairwise distances between the intervals in 
2.2. The Sum of Spheres in Bn
In the general form, the following statement holds true.
Lemma 3. The following formula is true:
Proof. By definition:
Thus, the above introduced parameter 
Lemma4. 
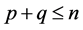
Proof. If
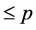


Then, from 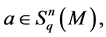


From here we get:
or:
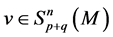
Hence,
And if


Hence,


Theorem 6. The following expression is true:
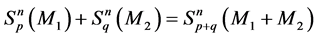
Proof. We have from Lemma 4:

Then, we have from Lemma 3:
And the proof is over.
Formula (12) defines the rule of “addition” for arbitrary spheres in the space
2.3. Sum of Layers in Bn
Let 
According to definition, 




Then, the following statement is true.
Lemma 5. The following expression holds true:
Proof. First, let us note the following.
If





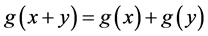

In standard terms, the symmetric group 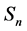
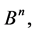

If
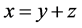





Taking this into account, to describe the set 

We discuss the following outline:
Here 
In the general case, the situation is absolutely analogous, and the weights are arranged as follows:
for
Here the condition for z holds true:
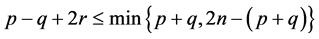
Examples.
1)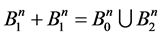
2)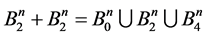
3)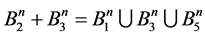
Theorem 7. The following expression is true:
where
Proof. From Lemmas 3 and 5, we have:
The proof is over.
2.4. Sum of Subspaces in Bn
As usual, let 
Statement 2.
and:
Statement 3. Let
And if:
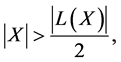
then the following equality is true:
Proof. We assume the contrary, that is,
Then, we have:


Hence, 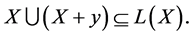
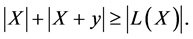
This contradicts the initial condition and the proof is over.
The following example shows that condition (12) is not necessary.
Example.
Let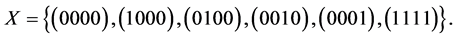

3. Equations in Sets
The “simplest” equation by sets is the following:
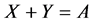
where
Equation (14) always has the trivial solution: 
The significance of Equation (14) is explained by the following circumstances.
1) The standard problems of covering and partitioning in the Boolean space Bn [6] can be formulated as problems of describing the set of solutions of Equation (14).
2) For certain additional conditions, the solution of Equation (14) forms a perfect pair (perfect code) in the additive channel of communication [9] .
3) The set of all solutions of Equation (14) coincides with the class of equivalence of the additive channel of communication [3] .
Examples.
1) If

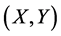
2) If A is a subspace of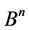

The following statements are true:
Statement 4. If the equations 

Proof. Let the pairs 



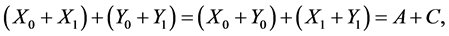
Statement 5. For 
has the solution
Statement 6. For 


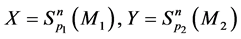
where
Statement 7. For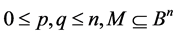


Statement 8. The sets of solutions 


Below, when discussing Equation (14), without violating generality, we may assume 
Statement 9. The equation 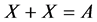
Proof. If 

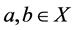




From here it follows that the equation 

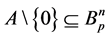
Statement 10. The equation 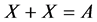

Let 
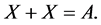
holds iff:
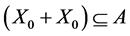

then the following statement is true.
Statement 11. If 
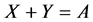




Statement 12. If A is a subspace from 
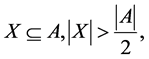
tion
In an additive channel of communication [3] an equivalence class has a unique representation by transitive sets of certain “generating” channels. The problem is to order these transitive sets by cardinalities of “generating” channels.
Let
We introduce the following parameters:
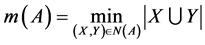
Such definition of 




One can easily prove that:

Statement 13. For the subspace 

Proof. It follows from (15) that it is sufficient to prove that the following equality is true:
Let 

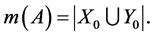
On the other hand, it follows from Statement 11 that 
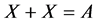

Theorem 8. The following estimations are true:
1) 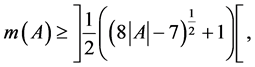
2) 

Proof. We have:
From this and definition of addition of sets we get:
Consequently:
To prove the 2nd estimation, we consider such subspaces 

Let:
where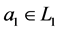
Let us prove that
We have:
As (Statement 12) 
Then, using:
we get:
Hence, taking this and Statement 13 into account we get:
The statement is proved.
Examples.
1) 
2)
but actually:
3) 
We consider the set:
We have: 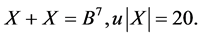
4)
We have:


But actually
Suggestion. For each 

Cite this paper
Vladimir Leontiev,Garib Movsisyan,Zhirayr Margaryan, (2016) Algebra and Geometry of Sets in Boolean Space. Open Journal of Discrete Mathematics,06,25-40. doi: 10.4236/ojdm.2016.62004
References
- 1. Nigmatulin, R.G. (1991) Complexity of Boolean Functions. Moscow, Nauka, 240 (in Russian).
- 2. McWilliams, F.J. and Sloane, N.J.A. (1977) The Theory of Error-Correcting Codes, Parts I and II. North-Holland Publishing Company, Amsterdam.
- 3. Leontiev, V.K. (2001) Selected Problems of Combinatorial Analysis. Bauman Moscow State Technical University, Moscow, 2001 (in Russian).
- 4. Leontiev, V.K. (2015) Combinatorics and Information. Moscow Institute of Physics and Technology (MIPT), Moscow, 2015 (in Russian).
- 5. Leontiev, V.K., Movsisyan, G.L. and Osipyan, A.A. (2014) Classification of the Subsets Bn, and the Additive Channels. Open Journal of Discrete Mathematics (OJDM), 4, 67-76.
- 6. Leontiev, V.K., Movsisyan, G.L., Osipyan, A.A. and Margaryan, Zh.G. (2014) On the Matrix and Additive Communication Channels. Journal of Information Security (JIS), 5, 178-191.
- 7. Leontiev, V.K., Movsisyan, G.L. and Margaryan, Zh.G. (2012) Constant Weight Perfect and D-Representable Codes. Proceedings of the Yerevan State University, Physical and Mathematical Sciences, 16-19.
- 8. Movsisyan, G.L. (1982) Perfect Codes in the Schemes Johnson. Bulletin of MSY, Computing Mathematics and Cybernetics, 1, 64-69 (in Russian).
- 9. Movsisyan, G.L. (2013) Dirichlet Regions and Perfect Codes in Additive Channel. Open Journal of Discrete Mathematics (OJDM), 3, 137-142.