Open Journal of Discrete Mathematics
Vol.06 No.01(2016), Article ID:61971,6 pages
10.4236/ojdm.2016.61001
Paired, Total, and Connected Domination on the Queen’s Graph Revisited
Paul A. Burchett
1005 Riverside Ave, Kingsport, USA

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 18 August 2015; accepted 14 December 2015; published 17 December 2015
ABSTRACT
The question associated with total domination on the queen’s graph has a long and rich history, first having been posed by Ahrens in 1910 [1] . The question is this: What is the minimum number of queens needed so that every square of an n × n board is attacked? Beginning in 2005 with Amirabadi, Burchett, and Hedetniemi [2] [3] , work on this problem, and two other related problems, has seen progress. Bounds have been given for the values of all three domination parameters on the queen’s graph. In this paper, formations of queens are given that provide new bounds for the values of total, paired, and connected domination on the queen’s graph, denoted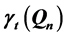 ,
, 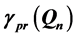 , and
, and 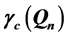 respectively. For any n × n board size, the new bound of
respectively. For any n × n board size, the new bound of 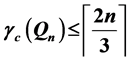 is arrived at, along with the separate bounds of
is arrived at, along with the separate bounds of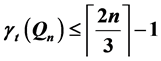 , for
, for 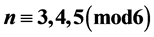 with
with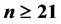 , and
, and , for
, for  with
with .
.
Keywords:
Chess, Total Dominating Set, Paired Dominating Set, Connected Dominating Set

1. Introduction
Interest in domination type problems began with the introduction of the Five Queen’s problem by De Jaenisch in 1862 [4] . Stated simply the Five Queen’s problem is this: What is the minimum number of queens needed to attack or occupy every square of a standard  chessboard? This problem has been extended in many different ways by mathematicians and chess enthusiasts to include generalizations of this problem to other pieces, board sizes, board types, domination parameters, etc. For a good survey on the extensions of this and other chess- related mathematics problems see [5] .
chessboard? This problem has been extended in many different ways by mathematicians and chess enthusiasts to include generalizations of this problem to other pieces, board sizes, board types, domination parameters, etc. For a good survey on the extensions of this and other chess- related mathematics problems see [5] .
It often helps when dealing with these types of problems to use the tools of graph theory. For example, the extension of the original problem to include any n × n board can be described by associating squares with vertices. Then, we form the n × n Queen’s graph, denoted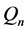 , by adding an edge between any two of our
, by adding an edge between any two of our 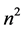 vertices whose corresponding squares share a common row, column, or diagonal. Any two vertices are said to be adjacent if they have an edge between them. The other extensions of De Jaenish’s original problem that will be dealt with in this paper are the considerations of three types of domination parameters on the n × n queen’s graph, namely those of total, paired, and connected domination.
vertices whose corresponding squares share a common row, column, or diagonal. Any two vertices are said to be adjacent if they have an edge between them. The other extensions of De Jaenish’s original problem that will be dealt with in this paper are the considerations of three types of domination parameters on the n × n queen’s graph, namely those of total, paired, and connected domination.
Along these lines, a set of queens is said to be a total dominating set if and only if every square on our n × n board is attacked. A set of queens is said to be a paired dominating set if and only if they attack every square of our n × n board, and there exists a perfect matching among the vertices corresponding to the squares occupied by queens. By perfect matching we mean that the queens can be grouped into disjoint sets of adjacent pairs, with all queens accounted for in exactly one of the sets. In this way, a paired dominating set of queens can be placed on the board, two at a time, in attacking pairs.
Lastly, a set of queens is a connected dominating set if and only if every square on our board is attacked or occupied, and given any two vertices corresponding to occupied squares there exists a path between these vertices consisting solely of vertices associated with occupied squares. In other words, one can move between any two vertices in the set using any number of movements among vertices in our set, but only by moving from vertex to vertex where adjacency exists―making sure to repeat no vertex. The minimum values among all total, paired, or connected dominating sets on the queen’s graph are denoted by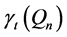 ,
, 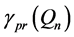 , and
, and 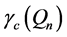
2. Results
Theorem 1. For all n,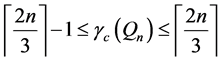
Proof: It should be noted that the lower bound of 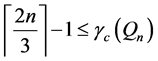
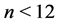
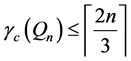
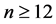
Suppose 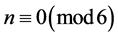

queens in every square to the right of the vertical axis of symmetry in the bottom row of the 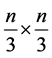
every square in the left-most column of region five below the horizontal axis of symmetry, every square in the top-most row of region five to the left of the vertical axis of symmetry, and finally, every square in the right- most column of region five above the horizontal axis of symmetry. Note our total count on the number of
queens is
To see that the queens form a connected set of queens, consider any two vertices corresponding to queens in the set. One can then denote a path between them where the vertices in our path correspond to a clockwise ordering of queens in our formation, beginning with either of the two considered vertices.
Next, to see that they are indeed a dominating set, consider regions two, four, five, six, and eight. It is easy to see that these regions are dominated either row-wise, column-wise, or both by the queens in region five.
Now consider the symmetric cases of regions one, three, seven, and nine. It is easy to see that these regions’
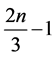
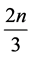
Figure 1. A formation of 16 connected and dominating set of queens on a 24 × 24 board.
and difference diagonal edge associated with the four queens along the two main diagonals.
For the case of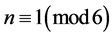
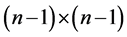
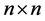
It is easy to see this is a connected dominating set of 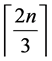
and the added queen occupies one of the main diagonals along with exactly two other queens in the set.
In the case where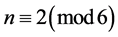
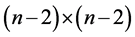
of the added rows and columns. Likewise, it is easy to see this forms a connected dominating set of 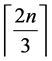
Now consider the case for 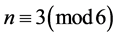
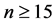
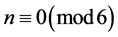
of queens thus far is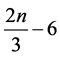
Next, place queens in the center of the left-most and right-most columns of region five and a queen in the center of the board. To cover the diagonals adjacent to the corner squares of region five we place queens on the
squares whose center has coordinates 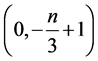
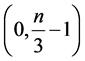

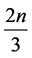
It is easy to see that, in a similar manner as for the case of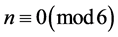
ly 
correspondence between the diagonals under consideration in these regions and the queens in the formation before the final queen is placed.
To see the cases where 
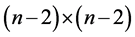



It should be noted that an upper bound of 
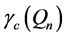

in [7] . This, along with the above theorem, reduces 
Figure 2. A formation of 14 connected and dominating set of queens on a 21 × 21 board. The queen placed last is in white.
with 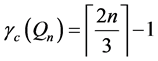

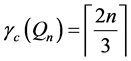
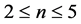
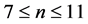
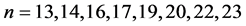
Lemma 1. For 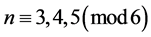
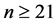
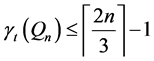
Proof: The proof for the upper bound is similar to Theorem 1 in that we use the same formation as in Figure 2, save for the final queen placed. There will be three components in the subgraph associated with our queens, each of which for 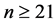
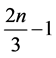
For the case where 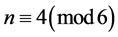
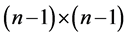
total dominating set of 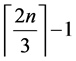
of our 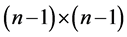
For the case where
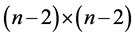
Lemma 2. For 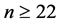
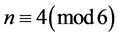
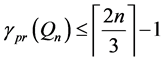
Proof: To see the proof use the same formation of total dominating queens as for the case of 
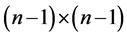
3. Summary
It should be noted that the lower bound of 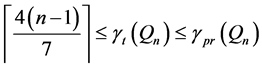
lower bound matches the known value for 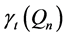
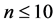

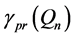
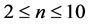
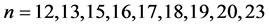
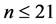
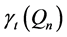

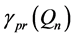
Conjecture 3.
For larger n, with

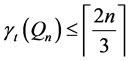
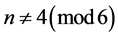
upper bound is provided by Welch’s formation of queens, or a slight manipulation of this formation for paired domination. Better upper bounds than those provided by either Welch’s formation, or those provided above for both 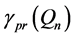
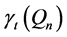
Cite this paper
Paul A.Burchett, (2016) Paired, Total, and Connected Domination on the Queen’s Graph Revisited. Open Journal of Discrete Mathematics,06,1-6. doi: 10.4236/ojdm.2016.61001
References
- 1. Ahrens, W. (1910) Mathematische unterhaltungen und spiele. B.G. Teubner, Leipzig-Berlin.
- 2. Amirabadi, A. (2005) Values of Total Domination Numbers and Connected Domination Numbers in the Queen’s Graph. Master’s Thesis, Clemson University, Clemson.
- 3. Burchett, P.A. (2006) Paired, Total and Connected Domination on the Queen’s Graph. Congressus Numerantium, 178, 207-222.
- 4. De Jaenisch, C.F. (1862) Applications de l’Analyse Mathematique au Jeu des Echecs. Petrograd.
- 5. Watkins, J.J. (2004) Across the Board: The Mathematics of Chessboard Problems. Princeton University Press, Princeton and Oxford.
http://dx.doi.org/10.1515/9781400840922 - 6. Haynes, T.W., Hedetniemi, S.T. and Slater, P.J., Eds. (1998) Domination in Graphs: Advanced Topics. Marcel Dekker, New York.
- 7. Burchett, P.A. (2011) On the Border Queens Problem and k-Tuple Domination on the Rook’s Graph. Congressus Numerantium, 209, 179-187.



