Received 19 February 2015; accepted 9 August 2015; published 12 August 2015

ABSTRACT

Fuzzy greedoids were recently introduced as a fuzzy set generalization of (crisp) greedoids. We characterize fuzzy languages which define fuzzy greedoids, give necessary properties and sufficient properties of the fuzzy rank function of a fuzzy greedoid, give a characterization of the rank function for a weighted greedoid, and discuss the rank closure of a fuzzy greedoid.

Keywords:

Fuzzy System Models, Greedoids, Fuzzy Rank Function

1. Introduction

In 1965 Zadeh [1] introduced the ideas of fuzzy set theory to study problems where partial membership in a set was appropriate. Since that time, work has progressed in extending his ideas to other areas of mathematics including analysis, linear algebra, and combinatorics.

In fact, starting in 1988, Goetschel Jr. and Voxman introduced the idea of a fuzzy matroid through a series of papers studying the many different cryptomorphic definitions of a crisp matroid [2] - [4] .

Only recently, in 2011, Al-Hawary [5] applied fuzzy set theory to the more general set system of a greedoid. Greedoids generalize both matroids and antimatroids, along with many other set systems. They arose from the study of the greedy algorithm and optimization [6] . See [7] for an thorough introduction to the study of greedoids.

Similar to matroids and other set systems, greedoids can be defined in a variety of ways, including as a set system, as an ordered language, from a rank function, and from a “closure operator”. In this article, we consider some of the other ways that fuzzy greedoids may be defined. We obtain a characterization of fuzzy greedoids in terms of fuzzy languages, and obtain necessary conditions and also sufficient conditions for a function to be a rank function of a fuzzy greedoids. Finally, we discuss the existence of a closure operator for a fuzzy greedoid.

In Section 2, we state the basic definitions and give a large class of examples of fuzzy greedoids. In Section 3, we introduce the ordered language interpretation of fuzzy greedoids. In the fourth section we discuss the rank function, introducing both sufficiently and separately necessary conditions for the rank function of general fuzzy greedoids. Additionally we obtain a characterization for the rank function of weighted greedoids (a large class of fuzzy greedoids). In Section 5 we discuss the existence of a rank closure operator in fuzzy greedoids. We finish with some open areas of research relating to fuzzy greedoids.

2. Definitions and Examples

Although it is possible to define fuzzy sets on any set, we are going to assume that the underlying set E is finite. A fuzzy set on E is a function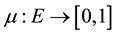. This generalizes the idea of a subset, which can be thought of as a function from E into. For each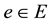, 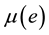is call the height of 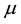at e. Similar to (crisp) set theory, there are some standard definitions and operations for fuzzy sets. We list these definitions below, with their corresponding names.

Definition 1. Suppose that 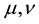are fuzzy sets on E and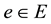. Then

1) 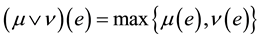(fuzzy union);

2) 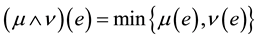(fuzzy intersection);

3) 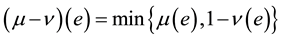(fuzzy set difference);

4) 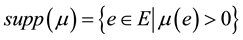(support of);

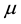5) 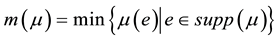(minimal height);

6) if and only if 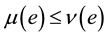for all;

7) if and only if and there exist such that;

8).

Finally, we let be the set of all fuzzy sets on E.

There is one particular type of fuzzy set which we will use extensively throughout the article―a spike― which we define here:

Definition 2. Suppose and. We define a spike to be the fuzzy set whose support is e and whose height at e is h.

Every fuzzy set can be thought of as a fuzzy union of spikes, as the following lemma, whose proof is straightforward, shows.

Lemma 3. Suppose with. If, then.

We now want to generalize the definition of a (crisp) greedoid to a fuzzy set version. The traditional definition of a greedoid in term of its feasible sets is given below. A thorough introduction to crisp greedoid theory can be found in [7] .

Definition 4. A finite set E and a collection of subsets of E forms a (crisp) greedoid if and only if

1);

2) For any with, there exists such that;

3) If with then there exists such that.

By considering this definition in terms of functions from E to, we can extend the definition of a greedoid to a fuzzy greedoid. We will use the definition given by Al-Hawary [5] .

Definition 5. Given a finite set E and a family of fuzzy sets satisfying the following two conditions:

(F1) For every with, there exists such that;

(F2) For any with, then there exist such that:

1);

2).

Then the fuzzy set system is called a fuzzy greedoid and the elements of are the feasible fuzzy sets of.

Because of their close relationship with crisp greedoids, a large number of examples of fuzzy greedoids can be obtained by adding a weight function to a greedoid, as the following proposition shows.

Proposition 6. Suppose is a crisp greedoid. Let be a weight function on E. If

then is a fuzzy greedoid.

Proof. All that is required is to show that satisfies both (F1) and (F2). Suppose. Since, there exist such that. Thus. This implies that satisfies (F1).

Suppose with. From the definition of a crisp greedoid, there exists such that. Let. It is clear that. Also, since or, satisfies (F2). Thus is a fuzzy greedoid.

With this proposition, it becomes easy to generate a large number of classes of examples of fuzzy greedoids. We give two such classes.

Example 1. (Weighted Branching Fuzzy Greedoids)

Suppose that is an undirected graph and is a vertex. The set of all edge sets of trees in which contain is the collection of feasible sets for the undirected branching greedoid of with root. Therefore, if is a weight function, then is the weighted undirected branching fuzzy greedoid of with root and weight function w. If is a directed graph, by using arborescences rooted at, we obtain the weighted directed branching fuzzy greedoid of with root and weight function w.

In particular, if is the following graph

and is defined by, , , then the following fuzzy set system is the feasible fuzzy sets of. (We use to denote the fuzzy set.)

Example 2. (Weighted Poset Greedoids)

Suppose P is a finite poset. The collection of ideals of P form the feasible sets for the poset greedoid of P. Let be a weight function, then by the previous proposition, is the weighted poset fuzzy greedoid of P.

In particular, if P has the following Hasse diagram.

If, , , then the following fuzzy set system if the feasible fuzzy set of.

Although weighted greedoids give a large number of examples of fuzzy greedoids, not every fuzzy greedoid can be defined as a weighted greedoid, as the following example shows:

Example 3. Let and for define and. If then it is easy to show that is a fuzzy greedoid.

However, as weighted greedoids, by definition, must have a finite collection of feasible fuzzy sets, this fuzzy greedoid cannot be a weighted greedoid.

3. Fuzzy Languages

In addition to a set system of feasible sets, a crisp greedoid can be defined as an ordered language with given properties. By defining a fuzzy language on a finite set, a fuzzy greedoid can be defined in the same manner. In this section, we determine the conditions necessary for a fuzzy language to define a fuzzy greedoid.

We begin by defining a fuzzy language on a set E.

Definition 7. Suppose. A fuzzy word on E is defined by

where for. A fuzzy language is a collection of fuzzy words. For every word there is a fuzzy set associated to it,

In a standard abuse of notation, we will use to denote. We will let 0 represent the empty word.

In order to show when a fuzzy language defines a fuzzy greedoid, we need to be able to go from a collection of fuzzy words to a collection of fuzzy sets, and vice versa. Suppose is a fuzzy language. Define the corresponding collection of fuzzy sets by.

For the other direction, Suppose is a fuzzy set system, with. Let and. Define a feasible ordering, on (on) if for all. For any collection of fuzzy sets, define to be the set of all feasible orderings of all fuzzy sets.

Given this ability to switch from a fuzzy language to a fuzzy set system, we now consider the properties that the languages for crisp greedoids have. Mirroring the properties possessed by crisp greedoids, we obtain the following theorem.

Theorem 1. Suppose E is a finite set and is a fuzzy language on E. Then forms the feasible fuzzy sets of a fuzzy greedoid if and only if

(L1);

(L2) If then;

(L3) If with then there exists with where.

Proof. We need to show that satisfies both (F1) and (F2). Let. There exists such that. Suppose. By property (L2),. Thus. Thus satisfies property (F1).

Let with. Thus there exists with and with. By property (L3), there exists such that where. Define. Thus and

Therefore satisfies (F2) and so a language satisfying properties (L1), (L2), (L3) determines a greedoid.

All that is left to show is that. Since satisfies (L2), this is straightforward and is omitted.

Similarly to crisp greedoids, Theorem 1 gives another cryptomorphic definition of a fuzzy greedoid. Next, we consider some of the functions that also give cryptomorphic definitions of crisp greedoids and consider their fuzzy versions. The two most common such functions are the rank function and the rank closure operator. We begin with the rank function for a fuzzy greedoid.

4. Rank Function

As with crisp greedoids, there is a natural definition of a rank function for fuzzy sets originally given in [5] .

Definition 8. If is a fuzzy greedoid on E, then the rank function is defined by.

Notice that for any fuzzy set, and, so.

Although we cannot guarantee that for any fuzzy set, there exists with and, we can get arbitrarily close, as stated in the next lemma.

Lemma 9. If is a fuzzy greedoid with rank function r and, then for any, there exists with and.

We first consider the properties possessed by r. In crisp greedoids, the rank function r is characterized by the following four properties (Theorem V.1.1 from [7] ):

1);

2) for any;

3) If then for any;

4) If, , , then.

The fuzzy equivalents of these four properties are:

(R1);

(R2) If, then;

(R3) If with, then;

(R4) If, , , and, then .

The natural question is whether these properties still hold for fuzzy greedoids, and if they do, whether they characterize the rank function of a fuzzy greedoid.

Proposition 10. If is a fuzzy greedoid with rank function then r satisfies properties (R1), (R2), (R3), and (R4).

Proof. (R1) is trivial. Since implies that, (R2) follows automatically.

Suppose with. Let with. Therefore. Thus, proving property (R3).

Suppose, , with. Let and. By Lemma 9, there exists with, and,. Let and be feasible orderings of and respectively.

By choice of, , so property (L3) implies that there exists such that. By choice of, this implies, and therefore or. Thus property (R4) is satisfied.

Given any rank function, we define a fuzzy set system as follows:. With Proposition 10, the next natural question is whether these four necessary properties are also sufficient for the rank function of a fuzzy greedoid. The answer to this is negative, as the following example shows.

Example 4. Let. Define A quick check shows that (R1), (R2), (R3), and (R4) hold for this rank function. Consider defined by. Since,. If with, then. So. Thus does not satisfy (F1).

However, with the following additional property, we do obtain a fuzzy greedoid.

(R5) If and, then for any,.

Before showing that a function satisfying (R1)-(R5) is the rank function of a fuzzy greedoid, we shall need the following lemma:

Lemma 11. Suppose satisfies properties (R1)-(R5) and

If and with, then.

Proof. Suppose with and for all i. Let.

If, then using (R2),

This is clearly a contradiction, so. Since, properties (R2) and (R5) imply that

Thus.

With this, we can now show:

Theorem 2. If a function satisfies (R1)-(R5) then r is a rank function for a fuzzy greedoid.

Proof. As above, let. We need to show that satisfies both (F1) and (F2).

The previous lemma shows that if and, then. Therefore satisfies (F1).

To show satisfies (F2), we assume that for all with, there is no such satisfying the requirements of (F2). Assume that and are a pair of fuzzy sets in with and also with minimal. We now obtain a contradiction.

Let be such that. If, then and

Contradicting the assumptions. Otherwise we obtain a pair, feasible sets with, and with

Continuing this process, we obtain a pair of feasible fuzzy sets, with and with and and.

Thus, using (R4), it is straightforward to show that there exists with. This contradicts the assumptions, thus showing that satisfies (F2).

Regretfully, not every rank function satisfies (R5), as the following example shows:

Example 5. For the following weighted rooted graph (rooted at, weights listed on the outside of each edge), consider its weighted undirected branching fuzzy greedoid.

Notice that and. Yet Therefore this fuzzy greedoid does not satisfy (R5).

This leads to the natural question:

Question 1. Determine necessary and sufficient conditions for a function to be a rank function for a fuzzy greedoid.

To finish this section, we will obtain a partial answer to the above question. We will now characterize the properties of a rank function for a weighted greedoid. From the work above, the rank function of a weighted greedoid clearly satisfies properties (R1)-(R4). It is easy to see that such a rank function also satisfies

(R5') For all, there exists such that for all, with, .

All that remains is to show that a function satisfying properties (R1)-(R4) and (R5') defines a weighted greedoid. We first show that it must define a fuzzy greedoid.

Lemma 12. If a function satisfies (R1)-(R4) and (R5'), then r is a rank function for a fuzzy greedoid.

Proof. Once again, define. We need to show that satisfies (F1) and (F2).

Suppose that. Since E is finite, by (R5'), if, then there exists with. Also, if and, then, otherwise, (R2) would be contradicted.

To show that satisfies (F1), suppose. For each, let. Let be such that is minimal. If then (F1) is satisfied, so assume that. Let be such that. Assume .

If, then, contradicting the assumption about f. Therefore. For any,. Therefore . These facts, along with (R4) implies that, which contradicts the definition of. Thus. Therefore, showing that satisfies (F1).

The proof to show that satisfies (F2) follows the exact steps of the proof of the previous theorem, however, instead of choosing elements a with minimal, at each step, choose an element a with minimal.

Theorem 3. Suppose that satisfies (R1)-(R4) and (R5'), then r is a rank function for a weighted greedoid.

Proof. As above, let, and let. The previous lemma shows that

is a fuzzy greedoid. The collection of supports of feasible fuzzy sets forms the collection of feasible sets in a greedoid. For each element, define. It is straightforward to show that is the collection of feasible fuzzy sets determined by the weights on the greedoid.

5. Rank Closure

We want to end with an example of the difference between crisp and fuzzy greedoids. In addition to feasible sets, ordered languages, and rank functions, crisp greedoids can be characterized by a closure operator. We will now show how the natural extension of the rank closure operator to fuzzy greedoids loses properties which would give a characterization of fuzzy greedoids. The natural extension is stated below:

Definition 13. Let. For each, define. With this, define the closure of, by

For crisp greedoids, the rank of a subset and the rank of the closure of the subset are equal. This property leads to a collection of properties which can be used to characterize the closure operator of a crisp greedoid. Regretfully, this property no longer holds for fuzzy greedoids, as the following example shows.

Example 6. Consider the weighted branching greedoid on the following weighted graph:

Notice that. For each,. Thus, implies (in fact).

6. Additional Research Areas

As fuzzy greedoids are a new area of interest, there are a lot of directions research can go to understand these objects. Most of these areas come directly from the crisp greedoid definitions. We now mention four such areas of investigation for fuzzy greedoids.

1) The poset greedoid mentioned in Section 2 is actually an example of a combinatorial structure called an antimatroid (see [7] for an introduction to antimatroids). The weighted version leads to a definition of a fuzzy antimatroid as follows:

Definition 14. Given a finite set E and a collection of fuzzy sets on E, the fuzzy set system is called a fuzzy antimatroid if

a) For every with, there exists such that.

b) If, then.

A lot of work has been done in characterizing antimatroids in terms of a closure operator, shelling processes, etc. Determine the fuzzy versions of these properties for antimatroids.

2) In 1989 Gordon and McMahon [8] introduced a characteristic polynomial for greedoids. This polynomial involved summing terms over all subsets of the ground set of the greedoid. Determine a fuzzy equivalent for the characteristic polynomial for fuzzy greedoids which extends the characteristic polynomial introduced by Gordon and McMahon.

3) In addition to the rank closure introduced here, greedoids possess another closure operator, the kernel closure. If is a crisp greedoid, then the kernel closure, , of a subset X is defined as . Determine a fuzzy equivalent of the kernel closure and discover the properties that this closure possesses.

4) In addition to matroids and antimatroids, there are many classes of greedoids which have been studied extensively. In [5] , Al-Hawary determined a fuzzy version for interval greedoids. There are also local poset greedoids, local forest greedoids, polymatroid, etc. (see [7] for definitions of these and other classes of greedoids). Determine fuzzy greedoid versions of these classes of greedoids, and determine which additional properties these classes of fuzzy greedoids must possess.

Acknowledgements

This research was supported by Summer Research Grants offered through Misericordia University.

Cite this paper

Steven J.Tedford, (2015) Rank Functions of Fuzzy Greedoids. Open Journal of Discrete Mathematics,05,65-73. doi: 10.4236/ojdm.2015.54006

References