Open Journal of Discrete Mathematics
Vol.05 No.02(2015), Article ID:56985,14 pages
10.4236/ojdm.2015.52002
Every Tiling of the First Quadrant by Ribbon L n-Ominoes Follows the Rectangular Pattern
Viorel Nitica
Department of Mathematics, West Chester University, West Chester, USA
Email: vnitica@wcupa.edu
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 7 October 2014; accepted 5 June 2015; published 9 June 2015
ABSTRACT
Let  and let
and let 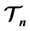 be the set of four ribbon L-shaped n-ominoes. We study tiling problems for regions in a square lattice by
be the set of four ribbon L-shaped n-ominoes. We study tiling problems for regions in a square lattice by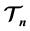 . Our main result shows a remarkable property of this set of tiles: any tiling of the first quadrant by
. Our main result shows a remarkable property of this set of tiles: any tiling of the first quadrant by , n even, reduces to a tiling by
, n even, reduces to a tiling by 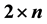 and
and 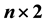 rectangles, each rectangle being covered by two ribbon L-shaped n-ominoes. An application of our result is the characterization of all rectangles that can be tiled by
rectangles, each rectangle being covered by two ribbon L-shaped n-ominoes. An application of our result is the characterization of all rectangles that can be tiled by , n even: a rectangle can be tiled by
, n even: a rectangle can be tiled by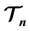 , n even, if and only if both of its sides are even and at least one side is divisible by n. Another application is the existence of the local move property for an infinite family of sets of tiles:
, n even, if and only if both of its sides are even and at least one side is divisible by n. Another application is the existence of the local move property for an infinite family of sets of tiles: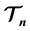 , n even, has the local move property for the class of rectangular regions with respect to the local moves that interchange a tiling of an
, n even, has the local move property for the class of rectangular regions with respect to the local moves that interchange a tiling of an  square by n/2 vertical rectangles, with a tiling by n/2 horizontal rectangles, each vertical/horizontal rectangle being covered by two ribbon L-shaped n- ominoes. We show that none of these results are valid for any odd n. The rectangular pattern of a tiling of the first quadrant persists if we add an extra
square by n/2 vertical rectangles, with a tiling by n/2 horizontal rectangles, each vertical/horizontal rectangle being covered by two ribbon L-shaped n- ominoes. We show that none of these results are valid for any odd n. The rectangular pattern of a tiling of the first quadrant persists if we add an extra 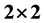 tile to
tile to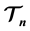 , n even. A rectangle can be tiled by the larger set of tiles if and only if it has both sides even. We also show that our main result implies that a skewed L-shaped n-omino, n even, is not a replicating tile of order k2 for any odd k.
, n even. A rectangle can be tiled by the larger set of tiles if and only if it has both sides even. We also show that our main result implies that a skewed L-shaped n-omino, n even, is not a replicating tile of order k2 for any odd k.
Keywords:
Polyomino, Replicating Tile, L-Shaped Polyomino, Skewed L-Shaped Polyomino, Local Move Property, Tiling Rectangles, Rectangular Pattern, Tiling First Quadrant

1. Introduction
In this article, we study tiling problems for regions in a square lattice by certain symmetries of an L-shaped polyomino. Polyomines were introduced by Golomb [1] and the standard reference about this subject is the book Polyominoes [2] . They are a never ending source of combinatorial problems.
The L-shaped polyomino we study is placed in a square lattice and is made out of 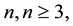 unit squares, or cells (see Figure 1(a)). In an
unit squares, or cells (see Figure 1(a)). In an 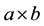 rectangle, a is the height and b is the base. We consider translations (only!) of the tiles shown in Figure 1(b). The first four are ribbon L-shaped n-ominoes and the last one is a
rectangle, a is the height and b is the base. We consider translations (only!) of the tiles shown in Figure 1(b). The first four are ribbon L-shaped n-ominoes and the last one is a 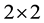 square. A ribbon polyomino [3] is a simply connected polyomino without two unit squares lying along a line
square. A ribbon polyomino [3] is a simply connected polyomino without two unit squares lying along a line
parallel to the first bisector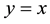 . We denote the set of tiles
. We denote the set of tiles ![]() by
by ![]() and the set of tiles
and the set of tiles ![]() by
by![]() .
.
The inspiration for this paper is the recent publication [4] , showing related results for the set of tiles consisting of four ribbon L-tetrominoes. That is, [4] investigates tiling problems for the set of tiles ![]() in the particular case
in the particular case![]() . In turn, the starting point for [4] was a problem from recreational mathematics. We recall that a replicating tile is one that can make larger copies of itself. The order of replication is the number of initial tiles that fit in the larger copy. Replicating tiles were introduced by Golomb in [5] and later widely promoted by Gardner in Scientific American [6] . Many replicating tiles are known. Some of them are polyominoes and some of them are of fractal nature. The topic is periodically revisited and further developed due to its relevance to various fields of contemporary mathematics such as combinatorics, discrete mathematics, theoretical computer science, fractal dimension, dynamical systems and probability theory, to name a few. The paper [7] investigated replication of higher orders for several replicating tiles introduced in [5] . In particular, it is suggested there that the skewed L-tetromino showed in Figure 2(a) is not replicating of order k2 for any odd k. The question is equivalent to that of tiling a k-inflated copy of the straight L-tetromino using only four out of eight possible orientations of an L-tetromino, namely those orientations that are ribbon. The question is solved in [4] .
. In turn, the starting point for [4] was a problem from recreational mathematics. We recall that a replicating tile is one that can make larger copies of itself. The order of replication is the number of initial tiles that fit in the larger copy. Replicating tiles were introduced by Golomb in [5] and later widely promoted by Gardner in Scientific American [6] . Many replicating tiles are known. Some of them are polyominoes and some of them are of fractal nature. The topic is periodically revisited and further developed due to its relevance to various fields of contemporary mathematics such as combinatorics, discrete mathematics, theoretical computer science, fractal dimension, dynamical systems and probability theory, to name a few. The paper [7] investigated replication of higher orders for several replicating tiles introduced in [5] . In particular, it is suggested there that the skewed L-tetromino showed in Figure 2(a) is not replicating of order k2 for any odd k. The question is equivalent to that of tiling a k-inflated copy of the straight L-tetromino using only four out of eight possible orientations of an L-tetromino, namely those orientations that are ribbon. The question is solved in [4] .
The discussion above shows that the limitation of the orientations of the tiles used in a tiling problem can be of interest. The extension of the results in [4] to the case of general ribbon L-shaped n-ominoes is a natural question. In particular, one may ask if the general skewed L-shaped n-omino showed in Figure 2(b) is a repli- cating tile of order k2 for any odd k. This question is equivalent to that of tiling a k-inflated copy of the straight L n-omino by![]() . A coloring invariant makes the proofs in [4] more transparent than here. The invariant does not easily generalize to this new situation and more involved geometric arguments are developed in this paper. The
. A coloring invariant makes the proofs in [4] more transparent than here. The invariant does not easily generalize to this new situation and more involved geometric arguments are developed in this paper. The
![]()
![]() (a) (b)
(a) (b)
Figure 1. (a) An L n-omino with n cells; (b) The set of tiles![]() .
.
![]()
![]() (a) (b)
(a) (b)
Figure 2. Skewed polyominoes. (a) Skewed L-tetromino; (b) Skewed L n-omino.
set of tiles ![]() is introduced due to the fact that most of the results for
is introduced due to the fact that most of the results for ![]() carry over to this larger set of tiles. Some proofs, nevertheless, are more involved.
carry over to this larger set of tiles. Some proofs, nevertheless, are more involved.
In order to avoid repetition, we assume for the rest of the paper that, unless otherwise specified (and this will be the case only in the introduction), n is even and![]() . We denote by
. We denote by ![]() the first quadrant with the unit square lattice.
the first quadrant with the unit square lattice.
Definition 1. A tiling of ![]() by
by ![]() follows the rectangular pattern if it reduces to a tiling by
follows the rectangular pattern if it reduces to a tiling by ![]() rectangles, with the last two types being covered by two ribbon L-shaped n-ominoes. More general, let P be a polygonal region in
rectangles, with the last two types being covered by two ribbon L-shaped n-ominoes. More general, let P be a polygonal region in ![]() based on the square lattice. Then a tiling of P that is part of a tiling of
based on the square lattice. Then a tiling of P that is part of a tiling of ![]() by
by ![]() follows the rectangular pattern if P is completely covered by non overlapping
follows the rectangular pattern if P is completely covered by non overlapping ![]() and
and ![]() rectangles having the coordinates of all vertices even and with each
rectangles having the coordinates of all vertices even and with each ![]() or
or ![]() rectangle covered by two ribbon L- shaped n-ominoes. Similar notions can be introduced for
rectangle covered by two ribbon L- shaped n-ominoes. Similar notions can be introduced for![]() .
.
Our main result is the following.
Theorem 1. Every tiling of ![]() by
by ![]() follows the rectangular pattern.
follows the rectangular pattern.
Theorem 1 is proved in Section 2.
It follows from Theorem 1 that:
Corollary 1. Every tiling of ![]() by
by ![]() follows the rectangular pattern.
follows the rectangular pattern.
Theorem 1 is optimal, as the following lemma shows.
Lemma 1. The addition of any even ´ odd or odd ´ odd rectangle to the set of tiles ![]() or
or ![]() allows for a tiling of
allows for a tiling of ![]() by
by ![]() (respectively
(respectively![]() ) that does not follow the rectangular pattern.
) that does not follow the rectangular pattern.
Proof. As the concatenation of two odd ´ odd rectangles is an even ´ odd rectangle, we can consider only the last type. Also, a concatenation of an odd number of copies of an even ´ odd rectangles can be used to construct an even ´ odd rectangle of arbitrary large length and height. Assuming the existence of such a rectangle in the tiling, a tiling of ![]() that does not follow the rectangular pattern is shown in Figure 3(a). The regions I, II, III are half-infinite strips of even width and region IV is a copy of the
that does not follow the rectangular pattern is shown in Figure 3(a). The regions I, II, III are half-infinite strips of even width and region IV is a copy of the![]() . All of them can be tiled by
. All of them can be tiled by ![]() or
or ![]() rectangles.
rectangles.
Some other consequences of the main result are listed below. The proofs of Corollaries 2, 3, 4 are similar to those of ( [4] , Corollary 2, 3, 4, 5).
Corollary 2. Every tiling of a rectangle by ![]() follows the rectangular pattern. Consequently, a rectangle can be tiled by
follows the rectangular pattern. Consequently, a rectangle can be tiled by ![]() if and only if both of its sides are even.
if and only if both of its sides are even.
Definition 2. A k-copy of a polyomino is a replica of it in which all ![]() squares are replaced by
squares are replaced by ![]() squares.
squares.
Corollary 3. Let ![]() be an odd integer. Then a k-copy of the ribbon L n-omino cannot be tiled by
be an odd integer. Then a k-copy of the ribbon L n-omino cannot be tiled by![]() . Consequently, the skewed L n-omino is not replicating of order k2 for any odd k.
. Consequently, the skewed L n-omino is not replicating of order k2 for any odd k.
Corollary 4. A half-infinite strip of odd width cannot be tiled by![]() .
.
The following problem is open for![]() . The case
. The case ![]() is solved in [4] using a coloring invariant.
is solved in [4] using a coloring invariant.
Problem 1. Show that a double infinite strip of odd width cannot be tiled by![]() .
.
It was proved by de Brujin [8] that a rectangle with integer sides can be tiled by ![]() and
and ![]() bars if and only if k divides one of the sides of the rectangle. Both
bars if and only if k divides one of the sides of the rectangle. Both ![]() and
and ![]() bars are ribbon polyominoes, see the definition above. De Brujin’s method uses a coloring invariant and can be easily adjusted to show:
bars are ribbon polyominoes, see the definition above. De Brujin’s method uses a coloring invariant and can be easily adjusted to show:
Lemma 2. A rectangle with integer sides can be tiled by ribbon polyominoes made of k cells if and only if k divides one of the sides of the rectangle.
![]()
![]() (a) (b)
(a) (b)
Figure 3. Tilings of Q1 that do not follow the rectangular pattern.
Proof. Assume that the rectangle is ![]() and has the lower left corner in the origin. Assigned to each cell in the rectangle the coordinates
and has the lower left corner in the origin. Assigned to each cell in the rectangle the coordinates ![]() of the upper right corner. Consider the sum:
of the upper right corner. Consider the sum:
![]()
and the double sum:
![]()
Each term in the last multiple sum corresponds to a cell in the rectangle. These terms can be grouped together in blocks of k terms each, combining terms corresponding to cells belonging the same ribbon polyomino with k cells. In such a group of terms, as we move from one end of the polyomino to the other, either the index ℓ1 decreases by 1, or the index ℓ2 decreases by 1 for each additional cell. It follows that the contribution of such a group to the double sum is zero. We infer that the double sum over all cells vanishes and therefore one of the factors ![]() equals zero.
equals zero.
On the other hand,
![]()
which forces A to be divisible by k if![]() . So one of the sides
. So one of the sides ![]() has to be divisible by k.
has to be divisible by k.
In conjunction with Theorem 1 this gives:
Theorem 2. Any tiling of a rectangle by ![]() follows the rectangular pattern. Consequently, a rectangle can be tiled by
follows the rectangular pattern. Consequently, a rectangle can be tiled by ![]() if and only if both sides are even and at least one of the sides is divisible by n.
if and only if both sides are even and at least one of the sides is divisible by n.
Not much is known about tiling integer sides rectangles with an odd side if we allow in the set of tiles all 8 orientations of an L-shaped n-omino, n even. It is known, and can be easily proved via a coloring argument, that if ![]() mod 4, then the area of a rectangle that can be tiled is a multiple of 2n. This condition is sufficient if
mod 4, then the area of a rectangle that can be tiled is a multiple of 2n. This condition is sufficient if ![]() and if the rectangle is not a bar of height 1, see for example [9] , but not in general.
and if the rectangle is not a bar of height 1, see for example [9] , but not in general.
The following result was found by Herman Chau, undergraduate student at Stanford University, during the Summer programme Research Experiences for Undergraduates, 2013, at Pennsylvania State University, Univer- sity Park.
Proposition 3. A rectangle of odd integer sides cannot be tiled by ![]() for any n, even or odd.
for any n, even or odd.
Proof. This is obvious if n is even. If n is odd, it follows from Lemma 2 that the rectangle has a side divisible by n. Then we employ a ribbon tiling invariant introduced by Pak [3] . Each ribbon tile of length n can be encoded uniquely as a binary string of length ![]() denoted
denoted ![]() where a 1 represents a down movement and a 0 represents a right movement. The encoding of a
where a 1 represents a down movement and a 0 represents a right movement. The encoding of a ![]() bar is
bar is ![]() for a
for a ![]() bar is
bar is ![]() and for the tiles in
and for the tiles in ![]() the encodings are shown in Figure 4.
the encodings are shown in Figure 4.
Pak showed that the function ![]() is an invariant of the set of ribbon tiles made of n-cells, which contains as a subset
is an invariant of the set of ribbon tiles made of n-cells, which contains as a subset![]() . In particular, one has that
. In particular, one has that
![]() (1)
(1)
for any tile in![]() . As the area of the rectangle is divisible by n, the rectangle can be tiled by
. As the area of the rectangle is divisible by n, the rectangle can be tiled by ![]() or
or ![]() bars. The invariant of a bar is 0, so the invariant of the whole rectangle is 0. Due to (1), the number of tiles that has to be used to obtain the 0 invariant is even, which is in contradiction with the area of the rectangle being odd.
bars. The invariant of a bar is 0, so the invariant of the whole rectangle is 0. Due to (1), the number of tiles that has to be used to obtain the 0 invariant is even, which is in contradiction with the area of the rectangle being odd.
![]()
Figure 4. The four L-shaped ribbon pentominoes and their encodings.
It would be interesting to find an elementary proof of Proposition 3 that is independent of Pak result. The result in Proposition 3 is not valid for the set of tiles![]() , as one can easily find a tiling of a
, as one can easily find a tiling of a ![]() rectangle by
rectangle by![]() .
.
No definitive results are known about tiling odd integer sides rectangles if the set of tiles consists of all 8 orientations of an L-shaped n-omino, n odd, despite serious computational effort invested in this question by various authors. We refer to the recent paper of Reid [10] for a more detailed discussion and for related references.
Figure 5(a) shows a tiling by ![]() of an infinite strip of even width
of an infinite strip of even width ![]() that does not follow the rectangular pattern. The tiling has only two tiles that are not part of rectangles, and this is the minimum number possible. Figure 5(b) shows a tiling of the second quadrant by
that does not follow the rectangular pattern. The tiling has only two tiles that are not part of rectangles, and this is the minimum number possible. Figure 5(b) shows a tiling of the second quadrant by ![]() that does not follow the rectangular pattern. It has only one tile that is not part of a rectangle. In both figures, the small rectangles are tiled by two ribbon L-shaped n-ominoes. The last example shows that our results do not remain valid for the reflections of the tiled region about the horizontal/vertical axis.
that does not follow the rectangular pattern. It has only one tile that is not part of a rectangle. In both figures, the small rectangles are tiled by two ribbon L-shaped n-ominoes. The last example shows that our results do not remain valid for the reflections of the tiled region about the horizontal/vertical axis.
Assume that n odd. Figure 6 shows how to tile a ![]() rectangle by
rectangle by![]() . The tiling has only two tiles that are not part of rectangles, and this is the minimum number possible. Each interior rectangle in Figure 6 can be covered by
. The tiling has only two tiles that are not part of rectangles, and this is the minimum number possible. Each interior rectangle in Figure 6 can be covered by ![]() or
or ![]() rectangles, which in turn are covered by two ribbon L-shaped n-ominoes. Thus the assumption that n is even is necessary in Theorems 1, 2, and Corollaries 2, 3, 4. Due to the example in Figure 6, tiling of certain half strips of odd width by
rectangles, which in turn are covered by two ribbon L-shaped n-ominoes. Thus the assumption that n is even is necessary in Theorems 1, 2, and Corollaries 2, 3, 4. Due to the example in Figure 6, tiling of certain half strips of odd width by![]() , is possible for any odd n.
, is possible for any odd n.
The following notions were introduced by Thurston [11] and were motivated by the work of Conway and Lagarias [12] .
Definition 3. Given a set of tiles ![]() and a finite set of local replacement moves
and a finite set of local replacement moves ![]() for the tiles in
for the tiles in![]() , we say that a region
, we say that a region ![]() has local connectivity with respect to
has local connectivity with respect to ![]() and
and ![]() if it possible to convert any tiling of
if it possible to convert any tiling of ![]() into any other by means of these moves. If
into any other by means of these moves. If ![]() is a class of regions, then we say that there is a local move property for
is a class of regions, then we say that there is a local move property for ![]() and
and ![]() if there exists a finite set of moves
if there exists a finite set of moves ![]() such that every
such that every ![]() in
in ![]() has local connectivity with respect to
has local connectivity with respect to ![]() and
and![]() .
.
![]()
![]() (a) (b)
(a) (b)
Figure 5. Tilings of an infinite strip of even width and of the second quadrant by Tn. (a) An infinite strip of even width; (b) The second quadrant.
![]()
Figure 6. A tiling of a (3n; 3n + 1) rectangle by Tn.
It is shown in [13] that if the set of tiles consists of ![]() and
and ![]() bars, then the class of rectangular regions has the local move property with respect to the moves that interchange a tiling of an
bars, then the class of rectangular regions has the local move property with respect to the moves that interchange a tiling of an ![]() square by k vertical bars with a tiling of the same
square by k vertical bars with a tiling of the same ![]() square by k horizontal bars. Moreover, it is obvious that if the set of tiles consists of
square by k horizontal bars. Moreover, it is obvious that if the set of tiles consists of ![]() bars and
bars and ![]() squares, then the class of rectangular regions has the local move property with respect to the moves that interchange a bar by k
squares, then the class of rectangular regions has the local move property with respect to the moves that interchange a bar by k ![]() squares tiling the bar.
squares tiling the bar.
In conjunction with Theorem 1, the remarks above give:
Theorem 4. The set of tiles ![]() has the local move property for the class of rectangular regions. The local moves interchange an
has the local move property for the class of rectangular regions. The local moves interchange an ![]() square tiled by n/2 vertical
square tiled by n/2 vertical ![]() rectangles with the same
rectangles with the same ![]() square tiled by n/2 horizontal
square tiled by n/2 horizontal ![]() rectangles. Each vertical/horizontal rectangle is tiled by two ribbon L-shaped n-ominoes.
rectangles. Each vertical/horizontal rectangle is tiled by two ribbon L-shaped n-ominoes.
Theorem 5. The set of tiles ![]() has the local move property for the class of rectangular regions. The local moves interchange an
has the local move property for the class of rectangular regions. The local moves interchange an ![]() or
or ![]() rectangle, tiled by two ribbon
rectangle, tiled by two ribbon ![]() -shaped
-shaped ![]() -ominoes, by n/2
-ominoes, by n/2 ![]() squares tiling the same rectangle.
squares tiling the same rectangle.
The set of local moves for ![]() is not a set of local moves for
is not a set of local moves for![]() , as one can consider two distinct tilings of a rectangle tiled by two tiles from
, as one can consider two distinct tilings of a rectangle tiled by two tiles from ![]() and several
and several ![]() squares. The set of local moves for
squares. The set of local moves for ![]() is not a set of local moves for
is not a set of local moves for![]() , as the
, as the ![]() square is not part of
square is not part of![]() .
.
Figure 7(a) shows the local moves for Tn and Figure 7(b) shows the local moves for ![]() in the particular case n = 6.
in the particular case n = 6.
The following two propositions are proved in Section 4.
Proposition 6. For general regions, and in particular for row-convex and column-convex regions, the set of tiles ![]() does not have the local move property.
does not have the local move property.
Proposition 7. For general regions, and in particular for row-convex and column-convex regions, the set of tiles ![]() does not have the local move property.
does not have the local move property.
One may wonder if a tiling by ![]() follows the rectangular pattern if other tiles besides rectangles are added to the tiling set. Figure 3(b) shows a tiling of a
follows the rectangular pattern if other tiles besides rectangles are added to the tiling set. Figure 3(b) shows a tiling of a ![]() rectangle by
rectangle by ![]() that does not follow the rectangular pattern. The regions I, II are
that does not follow the rectangular pattern. The regions I, II are ![]() squares and can be tiled by
squares and can be tiled by![]() . It is easy to see that this example can be generalized to the set of tiles
. It is easy to see that this example can be generalized to the set of tiles ![]() for any
for any ![]() with
with ![]() even.
even.
Figure 8 shows a more general family of tile sets, indexed by three positive integers, ![]() , and denoted
, and denoted![]() . The rectangles I are
. The rectangles I are![]() , the rectangles II are
, the rectangles II are ![]() and the rectangles III are
and the rectangles III are![]() . Note that
. Note that
![]() . We denote the tiles by
. We denote the tiles by ![]() The pairs
The pairs ![]() and
and ![]() consist of congruent tiles. The elements in each pair are symmetric about the first diagonal. As before, we may add an extra
consist of congruent tiles. The elements in each pair are symmetric about the first diagonal. As before, we may add an extra ![]() square to
square to ![]() and denote the new tile set by
and denote the new tile set by![]() . A tiling of
. A tiling of ![]() by
by ![]() is said to follows the rectangular
is said to follows the rectangular
pattern if it reduces to a tiling by ![]() rectangles, with the last two types tiled by
rectangles, with the last two types tiled by![]() .
.
Theorem 8. 1. If m odd, n even, p odd, any tiling of ![]() by
by ![]() (and consequently by
(and consequently by![]() ) follows the rectangular pattern.
) follows the rectangular pattern.
In the following cases tilings of ![]() by
by ![]() that do not follow the rectangular pattern are possible.
that do not follow the rectangular pattern are possible.
2. m even, n even, p even;
3. m even, n odd, p even;
4. m odd, n even, p even;
5. m even, n even, p odd;
6. m odd, n odd, p odd;
7. m odd, ![]() , p even;
, p even;
8. m even, ![]() , p odd;
, p odd;
9.![]() ,
, ![]() or
or![]() ,
,![]() ;
;
10.![]() ,
, ![]() ,
, ![]() or
or![]() ,
, ![]() ,
,![]() .
.
Case 1) in Theorem 8 is an immediate corollary of Theorem 1 due to the fact that the tiles in ![]() can be obtained from concatenation of tiles in
can be obtained from concatenation of tiles in![]() . The negative results in Theorem 8 are proved in Section 3. The cases m odd, n odd, p even and m even, n odd, p odd, not covered by Theorem 8, are left open.
. The negative results in Theorem 8 are proved in Section 3. The cases m odd, n odd, p even and m even, n odd, p odd, not covered by Theorem 8, are left open.
Let us summarize the main results of the paper and offer some perspective. We introduce a set of tiles that has some limitation in the orientations of the tiles. The set appears naturally from problems in recreational mathematics such as replicating properties of skewed polyominoes. For this set of tiles we are able to solve the problem of tiling of an arbitrary rectangle and are able to prove local move property.
We believe that the paper has certain heuristic value. Emerging from our work is a new method for discovering sets of tiles with interesting properties. We start by dissecting a rectangle, of base greater or equal then 2, in two irregular pieces. Then we symmetrize the pieces about the first bisector![]() . Finally, we consider the set consisting of these four tiles. The set of tiles usually has some limitation in the orientations of the tiles. This slightly unpleasant feature is, nevertheless, compensated by the properties that many times are present for the set of tiles, as exemplified in the paper. Other examples for which limitation of the orientations is required in order to have local move property are the set of n ribbon polyominoes from the work of Pak [3] and the set of two symmetries of the right tromino from the work of Conway and Lagarias [12] . Allowing all orientations usually leads to a more difficult problem. A first example that comes in mind is the problem of tiling a rectangle by L n-ominoes. In full generality this problem is widely open.
. Finally, we consider the set consisting of these four tiles. The set of tiles usually has some limitation in the orientations of the tiles. This slightly unpleasant feature is, nevertheless, compensated by the properties that many times are present for the set of tiles, as exemplified in the paper. Other examples for which limitation of the orientations is required in order to have local move property are the set of n ribbon polyominoes from the work of Pak [3] and the set of two symmetries of the right tromino from the work of Conway and Lagarias [12] . Allowing all orientations usually leads to a more difficult problem. A first example that comes in mind is the problem of tiling a rectangle by L n-ominoes. In full generality this problem is widely open.
Theorem 8 is included here in order to support the direction of research pointed above. The dissections appearing in Theorem 8 are those of rectangles of base equal to 2. When the height of the dissected rectangle is odd, the problem is completely solved by showing that always there exist tilings by the tile set that do not follow the rectangular pattern. The situation is more complex when the height of the dissected rectangle is even. If the tiles appearing from the dissection are congruent, the problem is completely solved. We identify both tiling sets that follow the rectangular pattern and tiling sets that do not follow the rectangular pattern. They appear in infinite families. If the tiles appearing from the dissection are not congruent, several cases are solved, identifying both types of tiling sets, and several cases are left open.
This suggests the following conjecture:
Conjecture 1. Fix a quadrant Q. If the height of the dissected rectangle is a multiple of the base, then both tiling sets that follow the rectangular pattern and tiling sets that do not follow the rectangular pattern are possible with respect to Q, for infinite families of rectangles and dissections.
More evidence supporting the conjecture is shown in the recent paper [14] , were certain dissections of rectangles of base equal to 3 and higher are considered, as well as tilings of all four quadrants.
2. Tiling Q1 by ![]()
In this section we prove Theorem 1. For simplicity we refer to the ![]() squares with even coordinates for all vertices as 2-squares.
squares with even coordinates for all vertices as 2-squares.
Definition 4. A ![]() tile that is part of a tiling of
tile that is part of a tiling of ![]() by
by ![]() is said to be in an irregular position if the coordinates of its lowest left corner are even, and if all 2-squares below and to the left of its lowest left corner follow the rectangular pattern. An irregular position for a
is said to be in an irregular position if the coordinates of its lowest left corner are even, and if all 2-squares below and to the left of its lowest left corner follow the rectangular pattern. An irregular position for a ![]() tile is defined via a reflection about the line
tile is defined via a reflection about the line![]() .
.
The ![]() tile in Figure 13(a) is in irregular position. All dark gray squares follows the rectangular pattern.
tile in Figure 13(a) is in irregular position. All dark gray squares follows the rectangular pattern.
Definition 5. Assume that ![]() is tiled by
is tiled by![]() . A gap is a rectangular region of height 2 made of cells that satisfies the following properties:
. A gap is a rectangular region of height 2 made of cells that satisfies the following properties:
1. The lower left corner has even coordinates;
2. The 2-squares on the left and below the upper level of the gap follow the rectangular pattern;
3. The 2-squares below the gap follow the rectangular pattern;
4. No part of the right side of an even length gap is covered by tiles;
5. The lower length 1 part of the right side of an odd length gap is not covered by tiles.
If the length of a gap is even, the gap is called even, otherwise the gap is called odd.
Pictures of gaps are shown in Figure 9. The gray 2-squares follow the rectangular pattern. For odd length gap this includes a rightmost 2-square that has only two cells directly below the gap. The thick segments on the right sides of the gaps, of length 2, respectively 1, are not covered by tiles and are actually part of the boundary of some tiles from the tiling of![]() .
.
For the following three lemmas we assume that a tiling of ![]() by
by ![]() is given.
is given.
Lemma 3. Assume that there exists an odd gap of length ![]() for which the leftmost
for which the leftmost ![]() -square does not follow the rectangular pattern. Then there exists a
-square does not follow the rectangular pattern. Then there exists a ![]() tile in an irregular position that is above the bottom of the gap and to the left of the right side of the gap.
tile in an irregular position that is above the bottom of the gap and to the left of the right side of the gap.
Proof. Let d be the distance between the right side of the gap and the y-axis. We proceed by induction on d. For the induction step, we show that a ![]() tile, or a new odd gap of length
tile, or a new odd gap of length ![]() with the leftmost 2-square not following the rectangular pattern, appears that is above or on the left side of the gap. In the diagrams, the initial odd gap is colored in light gray and the cells that cannot be tiled are colored in dark gray. When a new gap appears, it is covered by a pattern of north west parallel lines and labeled GAP. We will keep this conventions for the rest of the section.
with the leftmost 2-square not following the rectangular pattern, appears that is above or on the left side of the gap. In the diagrams, the initial odd gap is colored in light gray and the cells that cannot be tiled are colored in dark gray. When a new gap appears, it is covered by a pattern of north west parallel lines and labeled GAP. We will keep this conventions for the rest of the section.
We consider first the case when the left side of the gap is based on the y-axis. Here we will finish with a contradiction. This includes the base case ![]() for the induction. Look at the tiling of cell 1, the lowest leftmost in the gap. We cannot use a
for the induction. Look at the tiling of cell 1, the lowest leftmost in the gap. We cannot use a ![]() tile because of the hypothesis. We cannot use a
tile because of the hypothesis. We cannot use a ![]() tile because the gap is too close to the y-axis. If we use a
tile because the gap is too close to the y-axis. If we use a ![]() tile, then the leftmost 2-square in the gap is forced to follows the rectangular pattern, in contradiction to our assumption. Indeed, otherwise there exists a cell in the lower row of the gap that cannot be tiled. See Figure 10 for the diagrams of the cases that appear when we try to cover cell 2,
tile, then the leftmost 2-square in the gap is forced to follows the rectangular pattern, in contradiction to our assumption. Indeed, otherwise there exists a cell in the lower row of the gap that cannot be tiled. See Figure 10 for the diagrams of the cases that appear when we try to cover cell 2,
![]() (a) (b)
(a) (b)
Figure 9. Pictures of gaps. (a) An even gap; (b) An odd gap.
![]() (a) (b) (c) (d)
(a) (b) (c) (d)
Figure 10. A T1 tile covers the lower leftmost cell in the gap-the base case.
diagonally adjacent to 1. We only need a right edge of height 1 for the odd gap. If cell 1 is tiled by a ![]() tile, then cell 2 cannot be tiled without forcing the leftmost 2-square in the gap to follow the rectangular pattern or leading to a contradiction. See Figure 11 for the diagrams.
tile, then cell 2 cannot be tiled without forcing the leftmost 2-square in the gap to follow the rectangular pattern or leading to a contradiction. See Figure 11 for the diagrams.
Consider now the general case. We look at the tiling of cell 1, the lower leftmost in the gap. We cannot use a ![]() tile due to the hypothesis. If we use a
tile due to the hypothesis. If we use a ![]() tile, the
tile, the ![]() tile is in an irregular position. If we use a
tile is in an irregular position. If we use a ![]() tile, then the 2-square containing cell 1 has to follow the rectangular pattern. The reasoning is similar to that done in the case when the left side of the gap is supported by the y-axis and the same dark gray cells as in Figure 10 are impossible to tile. As cell 1 cannot be covered by a
tile, then the 2-square containing cell 1 has to follow the rectangular pattern. The reasoning is similar to that done in the case when the left side of the gap is supported by the y-axis and the same dark gray cells as in Figure 10 are impossible to tile. As cell 1 cannot be covered by a ![]() tile, it follows that cell 1 is covered by a
tile, it follows that cell 1 is covered by a ![]() tile. Consider cell 2 diagonally adjacent to cell 1. See Figure 12 for the diagrams of the cases that appear. In all cases a new odd gap is created which is closer to the y-axis then the original one. If the new odd gap has length 1, then it can be tiled only by a
tile. Consider cell 2 diagonally adjacent to cell 1. See Figure 12 for the diagrams of the cases that appear. In all cases a new odd gap is created which is closer to the y-axis then the original one. If the new odd gap has length 1, then it can be tiled only by a ![]() tile in an irregular position. Otherwise, look at the region inside the horizontal strip of width 2 containing the new odd gap that is bounded by the y-axis and the right side of the gap. If all 2-squares inside that region follow the rectangular pattern, the new odd gap can be taken to have length 1, and a
tile in an irregular position. Otherwise, look at the region inside the horizontal strip of width 2 containing the new odd gap that is bounded by the y-axis and the right side of the gap. If all 2-squares inside that region follow the rectangular pattern, the new odd gap can be taken to have length 1, and a ![]() tile in an irregular position appears. If there exists a 2-square that does not follow the rectangular pattern, choose the left side of the new odd gap to be the left side of the leftmost such square. This guarantees that the new odd gap has length
tile in an irregular position appears. If there exists a 2-square that does not follow the rectangular pattern, choose the left side of the new odd gap to be the left side of the leftmost such square. This guarantees that the new odd gap has length ![]() and has the leftmost 2-square not following the rectangular pattern.
and has the leftmost 2-square not following the rectangular pattern.
Lemma 4. Assume that the leftmost ![]() -square in an even gap of length
-square in an even gap of length ![]() does not follow the rectangular pattern. Then there exists a
does not follow the rectangular pattern. Then there exists a ![]() tile in an irregular position that is above the bottom of the gap and to the left of the right side of the gap.
tile in an irregular position that is above the bottom of the gap and to the left of the right side of the gap.
Proof. If![]() , due to the fact that the height of the right side of the gap is at least 2, the tiling of the gap is forced to follow the rectangular pattern. So we may assume
, due to the fact that the height of the right side of the gap is at least 2, the tiling of the gap is forced to follow the rectangular pattern. So we may assume![]() . If the left side of the gap is on the y-axis, a similar analysis to that in the proof of Lemma 3 leads to a contradiction. In particular the same dark gray cells marked in Figure 10 and Figure 11 remain impossible to tile. Consider the general case. We look at the lower leftmost cell in the gap, say 1. Reasoning as in the general case of the proof of Lemma 3, cell 1 has to be covered by a
. If the left side of the gap is on the y-axis, a similar analysis to that in the proof of Lemma 3 leads to a contradiction. In particular the same dark gray cells marked in Figure 10 and Figure 11 remain impossible to tile. Consider the general case. We look at the lower leftmost cell in the gap, say 1. Reasoning as in the general case of the proof of Lemma 3, cell 1 has to be covered by a ![]() tile. We look at the tiling of cell 2, diagonally adjacent to cell 1. Following the diagrams in Figure 12, this leads to an odd gap that is on the left and above the even gap. Now the existence of the
tile. We look at the tiling of cell 2, diagonally adjacent to cell 1. Following the diagrams in Figure 12, this leads to an odd gap that is on the left and above the even gap. Now the existence of the ![]() tile follows from Lemma 3 applied to the new odd gap.
tile follows from Lemma 3 applied to the new odd gap.
![]() (a) (b) (c) (d)
(a) (b) (c) (d)
Figure 11. A T3 tile covers the lower leftmost cell in the gap-base case.
![]() (a) (b) (c)
(a) (b) (c)![]() (d) (e)
(d) (e)
Figure 12. A T3 tile covers the lower leftmost cell in the gap-general case.
Lemma 5. Assume that a ![]() tile is placed in
tile is placed in ![]() in an irregular position. Then either all 2-squares to the left and below the
in an irregular position. Then either all 2-squares to the left and below the ![]() tile follow the rectangular pattern, or there exists a
tile follow the rectangular pattern, or there exists a ![]() tile that is closer to the y-axis and is in an irregular position.
tile that is closer to the y-axis and is in an irregular position.
Proof. Figure 13(a) illustrates the statement of the lemma: the dark gray 2-squares follow the rectangular pattern; either the light gray 2-squares follow the rectangular pattern, or there exists a ![]() tile in an irregular position that is closer to the y-axis. We proceed by contradiction and assume that not all light gray 2-squares follow the rectangular pattern. We identify the bottom row of width 2 in the light gray region in which appears such a square and apply Lemma 4 to an even gap in that row.
tile in an irregular position that is closer to the y-axis. We proceed by contradiction and assume that not all light gray 2-squares follow the rectangular pattern. We identify the bottom row of width 2 in the light gray region in which appears such a square and apply Lemma 4 to an even gap in that row.
Lemma 6. A tiling of ![]() by
by ![]() cannot contain a
cannot contain a ![]() or
or ![]() tile in an irregular position.
tile in an irregular position.
Proof. Assume that a ![]() tile is in an irregular position and at minimal distance from the y-axis. By Lemma 5, all 2-squares to the left and below the
tile is in an irregular position and at minimal distance from the y-axis. By Lemma 5, all 2-squares to the left and below the ![]() tile follow the rectangular pattern. The portion of the top row of the
tile follow the rectangular pattern. The portion of the top row of the ![]() tile that sits between the
tile that sits between the ![]() tile and the y-axis has an odd number of cells available. This creates an odd gap to which one applies Lemma 3 to deduce the existence of a new
tile and the y-axis has an odd number of cells available. This creates an odd gap to which one applies Lemma 3 to deduce the existence of a new ![]() tile in an irregular position that is based above and to the left of the initial
tile in an irregular position that is based above and to the left of the initial ![]() tile. This gives a contradiction.
tile. This gives a contradiction.
The statement about the ![]() tile follows due to the symmetry of
tile follows due to the symmetry of ![]() about the line
about the line![]() .
.
Proof of Theorem 1. We show that every 2-square follows the rectangular pattern. We do this by induction on a diagonal staircase at 2k, shown in Figure 13(b). We assume that every 2-square southwest of this line satisfies the hypothesis and we prove that every 2-square ![]() in Figure 13(b) also satisfies it. We first investigate the tiling of the corner cell of
in Figure 13(b) also satisfies it. We first investigate the tiling of the corner cell of![]() . If the cell is tiled by a
. If the cell is tiled by a ![]() tile, we are done. The other possible cases are shown in Figures 14(a) and Figures 14(b). Assume
tile, we are done. The other possible cases are shown in Figures 14(a) and Figures 14(b). Assume ![]() covers the corner square. If cell 1 is covered by
covers the corner square. If cell 1 is covered by ![]() or
or![]() , then cell 2 cannot be covered by any tile in
, then cell 2 cannot be covered by any tile in![]() . Thus cell 1 has to be covered by
. Thus cell 1 has to be covered by![]() , and we complete an
, and we complete an ![]() rectangle. The other case in Figure 14(b) is solved similarly, via a symmetry about
rectangle. The other case in Figure 14(b) is solved similarly, via a symmetry about![]() .
.
For the induction step we prove that the 2-squares ![]() in Figure 13(b) follow the rectangular pattern. Choose the rightmost square
in Figure 13(b) follow the rectangular pattern. Choose the rightmost square![]() , say X, which does not follow the rectangular pattern (see Figure 14(c)). Note that X is bounded below and two units to the right by the x axis or by two even
, say X, which does not follow the rectangular pattern (see Figure 14(c)). Note that X is bounded below and two units to the right by the x axis or by two even ![]() squares that follow the rectangular pattern, and it is bounded to the left by the y-axis or a 2-square that follows the rectangular pattern. By assumption, cell 1 cannot be tiled by a
squares that follow the rectangular pattern, and it is bounded to the left by the y-axis or a 2-square that follows the rectangular pattern. By assumption, cell 1 cannot be tiled by a ![]() tile. Also, cell 1 cannot be tiled by
tile. Also, cell 1 cannot be tiled by ![]() due to Lemma 6, as the
due to Lemma 6, as the ![]() tile is in an irregular position. We discuss the other cases below.
tile is in an irregular position. We discuss the other cases below.
![]() (a) (b)
(a) (b)
Figure 13. A T2 tile in an irregular position and the induction staircase line. (a) Lemma 5; (b) The induction staircase line.
![]() (a) (b) (c)
(a) (b) (c)
Figure 14. The steps of induction. (a) Base case: T1 covers the corner square; (b) Base case: T3 covers the corner square; (c) Inductive step.
Case 1. Let a ![]() tile cover cell 1 in Figure 14(c). If cell 2 is covered by
tile cover cell 1 in Figure 14(c). If cell 2 is covered by ![]() or
or![]() , then cell 3 cannot be covered by
, then cell 3 cannot be covered by![]() . The diagrams are similar to those in Figure 10. If cell 2 is covered by
. The diagrams are similar to those in Figure 10. If cell 2 is covered by![]() , then the square X is covered by an
, then the square X is covered by an ![]() rectangle.
rectangle.
Case 2. Assume that a ![]() tile covers cell 1 in Figure 14(c).
tile covers cell 1 in Figure 14(c).
Subcase 1. Assume that a ![]() or
or ![]() tile covers cell 2. We work now with Figure 15. Then an odd gap appears on the left side of the tile covering cell 2. From Lemma 3 it follows that there exists a
tile covers cell 2. We work now with Figure 15. Then an odd gap appears on the left side of the tile covering cell 2. From Lemma 3 it follows that there exists a ![]() tile in irregular position, which by Lemma 6 is in contradiction to the existence of a tiling for the
tile in irregular position, which by Lemma 6 is in contradiction to the existence of a tiling for the![]() .
.
Subcase 2. Assume that a ![]() tile covers cell 2. This completes a
tile covers cell 2. This completes a ![]() rectangle that covers X.
rectangle that covers X.
3. Proof of Theorem 8
In this section we show tilings of ![]() by
by ![]() that do not follow the rectangular pattern. We will use that a
that do not follow the rectangular pattern. We will use that a ![]() or a
or a ![]() rectangle, as well as an infinite half-strip of even width can be tiled by
rectangle, as well as an infinite half-strip of even width can be tiled by![]() .
.
Case 2. We place ![]() in the origin and cover the rest of
in the origin and cover the rest of ![]() by
by ![]() rectangles.
rectangles.
Case 3. We place ![]() and
and ![]() as in Figure 16(a). Rectangle I is
as in Figure 16(a). Rectangle I is![]() , with
, with ![]() even, the infinite half-strips II, IV and V are of even width, and region III is a copy of
even, the infinite half-strips II, IV and V are of even width, and region III is a copy of![]() .
.
Case 4. We place ![]() as shown in Figure 16(b). Rectangle I is
as shown in Figure 16(b). Rectangle I is![]() , infinite half-strips II and III are of even width, and region IV is a copy of
, infinite half-strips II and III are of even width, and region IV is a copy of![]() .
.
![]() (a) (b) (c)
(a) (b) (c)![]() (d) (e)
(d) (e)
Figure 15. Inductive step, Case 3.
![]()
![]() (a) (b)
(a) (b)
Figure 16. Cases 3 and 4: tilings that do not follow the rectangular pattern. (a) Case 3: m even, n odd, p even; (b) Case 4: m odd, n even, p even.
Case 5. This case is similar to Case 3.
Case 6. Figure 17 shows a tiling of a ![]() rectangle, and thus of
rectangle, and thus of![]() , by
, by ![]() that does not follow the rectangular pattern. We place two copies of
that does not follow the rectangular pattern. We place two copies of ![]() and two copies of
and two copies of ![]() inside the rectangle
inside the rectangle
as in Figure 17. Rectangles I and VIII are![]() , with
, with ![]() even, rectangles II and VI are
even, rectangles II and VI are![]() , with
, with ![]() even, rectangles III and VII are
even, rectangles III and VII are![]() , and rectangles IV and V are
, and rectangles IV and V are![]() .
.
Cases 7 and 8. We consider two cases. In Figure 18(a), we place copies of ![]() in
in ![]() as shown. Infinite half-strips I, II, IV are of even width and region III is a copy of
as shown. Infinite half-strips I, II, IV are of even width and region III is a copy of![]() . In Figure 18(b), we place copies of
. In Figure 18(b), we place copies of ![]() in
in ![]() as shown. Infinite half-strips I, II, IV are of even width and region III is a copy of
as shown. Infinite half-strips I, II, IV are of even width and region III is a copy of![]() .
.
Cases 9 and 10. Figure 19 shows a tiling of ![]() by
by ![]() that does not follow the rectangular pattern.
that does not follow the rectangular pattern.
![]()
Figure 17. Case 6: m odd, n odd, p odd: tilings that do not follow the rec- tangular pattern.
![]()
![]() (a) (b)
(a) (b)
Figure 18. Cases 7 and 8: tilings that do not follow the rectangular pattern. (a) Case 7: m odd, n = 1, p even; (b) Case 8 m even, n = 1, p odd.
![]()
![]() (a) (b)
(a) (b)
Figure 19. Cases 9 and 10: tilings that do not follow the rectangular pattern. (a) Case 9: m = n = 3, p = 2; (b) Case 10: m = 1, n = 3, p = 2.
4. Failure of Local Move Property for General Regions
In this section, we prove Proposition 6 and Proposition 7.
Proof of Proposition 6. For each fixed n, there exists an infinite family of row-convex (and column-convex) regions that admit only two tilings by![]() . Figure 20(a) shows one instance, for
. Figure 20(a) shows one instance, for![]() . In general, there are n/2 rectangles of size
. In general, there are n/2 rectangles of size ![]() in the region, one at the top and
in the region, one at the top and ![]() at the bottom. The infinite family of regions is obtained by introducing more copies of the gray subregion in the middle. For
at the bottom. The infinite family of regions is obtained by introducing more copies of the gray subregion in the middle. For![]() , the two tilings are shown in Figure 20(b). We observe that the cell labeled * in the region can be covered in only two ways by tiles in
, the two tilings are shown in Figure 20(b). We observe that the cell labeled * in the region can be covered in only two ways by tiles in![]() . Once the tile covering * is placed, the tiling of the rest of the region is forced. Note that in the left subfigure of Figure 20(b) covering one of the cells labeled
. Once the tile covering * is placed, the tiling of the rest of the region is forced. Note that in the left subfigure of Figure 20(b) covering one of the cells labeled ![]() by a vertical
by a vertical ![]() tile forces the remaining
tile forces the remaining ![]() cells to be covered by
cells to be covered by ![]() tiles, and consequently cell
tiles, and consequently cell ![]() in the lower left corner becomes impossible to cover. The circular pattern observed in Figure 20(b), where the tiles are labeled in the order of their forced placement, obviously holds for any n and any instance of the region.
in the lower left corner becomes impossible to cover. The circular pattern observed in Figure 20(b), where the tiles are labeled in the order of their forced placement, obviously holds for any n and any instance of the region.
Proof of Proposition 7. For each fixed n, there exists an infinite family of row-convex (and column-convex)
regions, each instance of the region having exactly ![]() tilings by
tilings by![]() . Figure 21 shows one instance, for
. Figure 21 shows one instance, for![]() . In general, there are n/2 rectangles of size
. In general, there are n/2 rectangles of size ![]() in the figure, placed either one at the top and
in the figure, placed either one at the top and ![]() at the bottom, or placed one on the left side and
at the bottom, or placed one on the left side and ![]() on the right side (see Figure 21). As before, the infinite
on the right side (see Figure 21). As before, the infinite
family of regions is obtained by introducing more copies of the gray subregion in the middle. After factoring the ![]() tilings by
tilings by ![]() by the moves shown in Figure 7(b), we are still left with two classes that cannot be connected, so an extra local move is necessary. For
by the moves shown in Figure 7(b), we are still left with two classes that cannot be connected, so an extra local move is necessary. For ![]() and for the region shown in Figure 21, a possible local move that connects the classes above is shown in Figure 20(b). So for n fixed, each instance of the region introduces an extra local move, leading to an infinite set of local moves, in contradiction to local move property.
and for the region shown in Figure 21, a possible local move that connects the classes above is shown in Figure 20(b). So for n fixed, each instance of the region introduces an extra local move, leading to an infinite set of local moves, in contradiction to local move property.
The number of tilings by ![]() is exactly
is exactly ![]() due to the fact that any tiling reduces to one of those shown in Figure 21. The
due to the fact that any tiling reduces to one of those shown in Figure 21. The ![]() and
and ![]() rectangles shown in the figure are either tiled by two tiles from
rectangles shown in the figure are either tiled by two tiles from ![]() or by n/2
or by n/2 ![]() squares. We discuss the proof in the case
squares. We discuss the proof in the case![]() , and for the instance of the region shown in Figure 21, but our argument obviously holds for any n and any instance of the region. Observe first that no
, and for the instance of the region shown in Figure 21, but our argument obviously holds for any n and any instance of the region. Observe first that no ![]() tile can
tile can
![]() (a) (b)
(a) (b)
Figure 21. A region that is tiled in ![]() ways by
ways by![]() .
.
cover a cell in the top row of the region. Indeed, if this is the case, on the right side of the ![]() tile we have room only for vertical tiles and
tile we have room only for vertical tiles and ![]() squares. This forces the right side of the box to be tiled regularly by
squares. This forces the right side of the box to be tiled regularly by ![]() squares or by a
squares or by a ![]() rectangle tiled by two vertical tiles (see Figure 22(a)). Cell * can be covered only by a
rectangle tiled by two vertical tiles (see Figure 22(a)). Cell * can be covered only by a ![]() tile. Then, cell ** immediately below the
tile. Then, cell ** immediately below the ![]() tile is impossible to cover. By a similar argument, if a
tile is impossible to cover. By a similar argument, if a ![]() tile covers a cell in the top row of the region, then we have the partial tiling from Figure 22(b), in which the subregion on the right side of the
tile covers a cell in the top row of the region, then we have the partial tiling from Figure 22(b), in which the subregion on the right side of the ![]() tile is tiled by
tile is tiled by ![]() squares and
squares and ![]() rectangles. We observe that in this case the first tile (from the left) covering a cell in the top row cannot be a
rectangles. We observe that in this case the first tile (from the left) covering a cell in the top row cannot be a ![]() square, because this will lead to a contradiction as in the proof of Proposition 6. Indeed, there is no room for a horizontal tile below the
square, because this will lead to a contradiction as in the proof of Proposition 6. Indeed, there is no room for a horizontal tile below the ![]() square due to the presence of the vertical
square due to the presence of the vertical ![]() tile, so that tile has to be a
tile, so that tile has to be a ![]() tile and indeed the
tile and indeed the ![]() tile in Figure 22(b) covers the first cell from the top row. The rest of the tiling (modulo again the argument by contradiction from the proof of Proposition 6) is forced and leads to the tiling shown in the right subfigure of Figure 21.
tile in Figure 22(b) covers the first cell from the top row. The rest of the tiling (modulo again the argument by contradiction from the proof of Proposition 6) is forced and leads to the tiling shown in the right subfigure of Figure 21.
If an horizontal ![]() tile covers the cell, or if the whole row of length 2 at the top of the figure is covered by
tile covers the cell, or if the whole row of length 2 at the top of the figure is covered by ![]() squares, then a discussion similar to that done for
squares, then a discussion similar to that done for ![]() leads to the partial tiling shown in Figure 23(a). We look at cell
leads to the partial tiling shown in Figure 23(a). We look at cell![]() , which can be covered only by a
, which can be covered only by a ![]() square or a
square or a ![]() tile. If cell
tile. If cell ![]() is covered by a
is covered by a ![]() square, then cell
square, then cell ![]() can be covered only by a
can be covered only by a ![]() tile, creating a region on the right side of the
tile, creating a region on the right side of the ![]() tile that cannot be tiled (see Figure 23(b)). Therefore, cell
tile that cannot be tiled (see Figure 23(b)). Therefore, cell ![]() is covered by a vertical
is covered by a vertical ![]() tile and applying the previous argument repeatedly forces the partial tiling from Figure 23(c). We look at cell
tile and applying the previous argument repeatedly forces the partial tiling from Figure 23(c). We look at cell![]() , which can be covered without an immediate contradiction only by a
, which can be covered without an immediate contradiction only by a ![]() square or a
square or a ![]() tile. If cell
tile. If cell ![]() is covered by a
is covered by a ![]() tile, then we are left with a region that can be tiled only in the special way from Figure 21. If cell
tile, then we are left with a region that can be tiled only in the special way from Figure 21. If cell ![]() is covered by a
is covered by a ![]() square, this leads to the partial tiling from Figure 23(d), which contains a region that cannot be tiled by
square, this leads to the partial tiling from Figure 23(d), which contains a region that cannot be tiled by![]() . We conclude that cell
. We conclude that cell ![]() is covered by a vertical
is covered by a vertical ![]() tile, which leads to the tiling shown in the left subfigure of Figure 21.
tile, which leads to the tiling shown in the left subfigure of Figure 21.
Acknowledgements
V. Nitica was partially supported by Simons Foundation Grant 208729. The author would like to thank several anonymous reviewers that read versions of the paper for their patience, for their generosity in sharing new ideas, and for many helpful suggestions that contributed to the improvement of this paper. The author would also like
to thank the following undergraduate students that worked with him at various tiling projects during the Summer programmes Research Experiences for Undergraduates, 2012, 2013, 2014, at Pennsylvania State University, University Park: M. Chao, D. Levenstein, R. Sharp, H. Chau, A. Calderon, S. Fairchild, S. Simon. Frequent discussions with them help the author better formalize the results in this paper.
References
- Golomb, S.W. (1954) Checker Boards and Polyominoes. The American Mathematical Monthly, 61, 675-682. http://dx.doi.org/10.2307/2307321
- Golomb, S.W. (1994) Polyominoes, Puzzles, Patterns, Problems, and Packings. 2nd Edition, Princeton University Press, Princeton.
- Pak, I. (2000) Ribbon Tile Invariants. Transactions of the American Mathematical Society, 352, 5525-5561. http://dx.doi.org/10.1090/S0002-9947-00-02666-0
- Chao, M., Levenstein, D., Nitica, V. and Sharp, R. (2013) A Coloring Invariant for Ribbon L-Tetrominoes. Discrete Mathematics, 313, 611-621. http://dx.doi.org/10.1016/j.disc.2012.12.007
- Golomb, S.W. (1964) Replicating Figures in the Plane. The Mathematical Gazette, 48, 403-412. http://dx.doi.org/10.2307/3611700
- Gardner, M. (1963) On “Rep-Tiles”, Polygons That Can Make Larger and Smaller Copies of Themselves. Scientific American, 208, 154-157. http://dx.doi.org/10.1038/scientificamerican0563-154
- Nitica, V. (2003) Rep-Tiles Revisited, in the Volume MASS Selecta: Teaching and Learning Advanced Undergraduate Mathematics, American Mathematical Society, Providence.
- de Brujin, N.G. (1969) Filling Boxes with Bricks. The American Mathematical Monthly, 76, 37-40. http://dx.doi.org/10.2307/2316785
- Nitica, V. (2004-2005) Tiling a Deficient Rectangle by L-Tetrominoes. Journal of Recreational Mathematics, 33, 259- 271.
- Reid, M. (2014) Many L-Shaped Polyominoes Have Odd Rectangular Packings. Annals of Combinatorics, 18, 341- 357. http://dx.doi.org/10.1007/s00026-014-0226-9
- Thurston, W. (1990) Conway’s Tiling Groups. The American Mathematical Monthly, 97, 757-773. http://dx.doi.org/10.2307/2324578
- Conway, J.H. and Lagarias, J.C. (1990) Tilings with Polyominoes and Combinatorial Group Theory. Journal Combinatorial Theory, Series A, 53, 183-208. http://dx.doi.org/10.1016/0097-3165(90)90057-4
- Kenyon, C. and Kenyon, R. (1992) Tiling a Polygon with Rectangles. Proceedings of 33rd Annual Symposium on Foundations of Computer Science (FOCS), Pittsburgh, 24-27 October 1992, 610-619.
- Calderon, A., Fairchild, S., Nitica, V. and Simon, S. (2015) Tilings of Quadrants by L-Ominoes and Notched Rectangles. Topics in Recreational Mathematics, 5.



 and let
and let 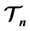 be the set of four ribbon L-shaped n-ominoes. We study tiling problems for regions in a square lattice by
be the set of four ribbon L-shaped n-ominoes. We study tiling problems for regions in a square lattice by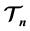 . Our main result shows a remarkable property of this set of tiles: any tiling of the first quadrant by
. Our main result shows a remarkable property of this set of tiles: any tiling of the first quadrant by , n even, reduces to a tiling by
, n even, reduces to a tiling by 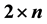 and
and 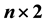 rectangles, each rectangle being covered by two ribbon L-shaped n-ominoes. An application of our result is the characterization of all rectangles that can be tiled by
rectangles, each rectangle being covered by two ribbon L-shaped n-ominoes. An application of our result is the characterization of all rectangles that can be tiled by , n even: a rectangle can be tiled by
, n even: a rectangle can be tiled by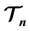 , n even, if and only if both of its sides are even and at least one side is divisible by n. Another application is the existence of the local move property for an infinite family of sets of tiles:
, n even, if and only if both of its sides are even and at least one side is divisible by n. Another application is the existence of the local move property for an infinite family of sets of tiles: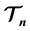 , n even, has the local move property for the class of rectangular regions with respect to the local moves that interchange a tiling of an
, n even, has the local move property for the class of rectangular regions with respect to the local moves that interchange a tiling of an  square by n/2 vertical rectangles, with a tiling by n/2 horizontal rectangles, each vertical/horizontal rectangle being covered by two ribbon L-shaped n- ominoes. We show that none of these results are valid for any odd n. The rectangular pattern of a tiling of the first quadrant persists if we add an extra
square by n/2 vertical rectangles, with a tiling by n/2 horizontal rectangles, each vertical/horizontal rectangle being covered by two ribbon L-shaped n- ominoes. We show that none of these results are valid for any odd n. The rectangular pattern of a tiling of the first quadrant persists if we add an extra 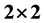 tile to
tile to , n even. A rectangle can be tiled by the larger set of tiles if and only if it has both sides even. We also show that our main result implies that a skewed L-shaped n-omino, n even, is not a replicating tile of order k2 for any odd k.
, n even. A rectangle can be tiled by the larger set of tiles if and only if it has both sides even. We also show that our main result implies that a skewed L-shaped n-omino, n even, is not a replicating tile of order k2 for any odd k.
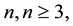 unit squares, or cells (see Figure 1(a)). In an
unit squares, or cells (see Figure 1(a)). In an 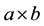 rectangle, a is the height and b is the base. We consider translations (only!) of the tiles shown in Figure 1(b). The first four are ribbon L-shaped n-ominoes and the last one is a
rectangle, a is the height and b is the base. We consider translations (only!) of the tiles shown in Figure 1(b). The first four are ribbon L-shaped n-ominoes and the last one is a 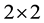 square. A ribbon polyomino [3] is a simply connected polyomino without two unit squares lying along a line
square. A ribbon polyomino [3] is a simply connected polyomino without two unit squares lying along a line . We denote the set of tiles
. We denote the set of tiles 

























































































































































































































































































































































































































