Received 24 November 2014; revised 20 December 2014; accepted 3 January 2015

ABSTRACT

A new combinatorial interpretation of Raney numbers is proposed. We apply this combinatorial interpretation to solve several tree enumeration counting problems. Further a generalized Catalan triangle is introduced and some of its properties are proved.

Keywords:

Raney Numbers, Fuss-Catalan Numbers, Tree Enumeration, Network

1. Introduction

Interestingly Penson and Zyczkowski were the first who use the term Raney numbers [1] [2] and it is defined as

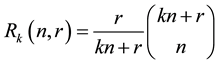where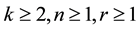. Nevertheless, it is known that Raney’s lemma could be

used in counting problem associated with Catalan numbers [3] and a bijection exists between Raney path and plan multitree [4] .

These numbers do not form novel sequences, as the numbers were introduced earlier as a generalization of the binomial series [5] . Moreover, the sequence

is not included in OEIS database [6] before 2011. If we let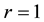, we obtain another known sequence, i.e.,

Fuss-Catalan numbers [7] [8] which is defined as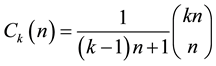. Although Fuss-Catalan numbers

were introduced earlier than Catalan numbers [9] , the Catalan numbers are more popular and widely used than the Fuss-Catalan numbers (see [10] [11] for details). Due to its self similar structure, the applications of Catalan numbers could be found in many physical problems, e.g., lattice model [12] , tree enumeration network [13] , and Hankel matrices in coding theory [14] . A tree is a connected graph with no cycles and for which only one shortest path exists from one node to another. Tree enumeration is an important tool to study network. These networks always grow in a power-law behavior which is often found in social network, subway system [15] , etc.

In this paper, we introduce Raney numbers 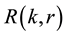in the form of a non-linear recursion and then we pro- vide a combinatorial interpretation of Raney numbers. Using this combinatorial interpretation, we solve several tree enumeration counting problems in which we recover the well-known Fuss-Catalan numbers [16] , Catalan triangles [17] , and other less known numbers. Motivated by the connection between Raney numbers and Catalan triangles, a generalization of Catalan triangles is proposed and we prove some of their properties. Consequently these formulas generalize the properties of Catalan triangles. From the exact solution of these tree enumeration problems, we are able to find a sharp upper bound of the number of each tree enumeration problem. The upper bound is important in the contour method for lattice models and limit of the random graph.

2. Raney Numbers

Let be the number of a -ary trees with labeled vertices (Figure 1), where

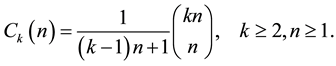
The Raney numbers are defined as follows:

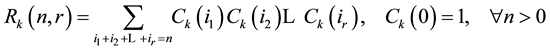(1)

where. Therefore, the combinatorial interpretation is as follows: 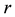copies of 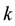-ary tree with total number of vertices.

Next, we let 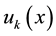be the generating function for, i.e.,

Then, the generating function of is and the Raney numbers satisfy the following formula [18] .

Lemma 1. Let be the generating function of the Raney numbers. Then,

(2)

Immediately, we obtain the following theorem.

Theorem 1. The binomial forms of the Raney numbers are given by

(3)

From theorem (1), it is not difficult to deduce some of the properties of Raney numbers.

Corollary 1. For integer, we have

(4)

(5)

(6)

(7)

Corollary 2. We can write in a nonlinear recursion as:

(8)

where.

We recover the formula by joining the copies of -ary tree with vertices which is also equivalent to a -ary tree with vertices and an additional root (see Figure 2):

Using binomial form of, one can obtain the following result.

Corollary 3. For a fixed integer, and,

(9)

where if.

For, we recover the identity of a generalized Ballot numbers:

(10)

3. A Homogeneous k-Ary Tree

Unlike the usual -ary tree, we define a homogeneous -ary tree as a graph with no cycles, in which each vertex emanates edges (see Figure 3 for k = 4). We fix a vertex namely as the root. Unlike the ordinary root in a -ary tree, this root has successors while other vertices have number of successors. Any vertex could be chosen to be the root since the graph is homogenous. For a given vertices, we may find how many connected sub-tree rooted at. This number is defined as.

Theorem 2. For, we can write in a nonlinear recursion of as:

(11)

Proof. We decompose the problem by finding out the number of -ary tree of number of one copy of -ary tree with vertices, i.e., , and another copy of -ary tree with vertices, i.e..

Since the former must always include, its range should be from 1 to. Total is just the sum of all using the addition and multiplication principles.

Using Equation (8), we rewrite the formula above as

(12)

This formula can also be obtained using copies of -ary tree together with vertices and one center.

We then find the binomial form of.

Corollary 4. For, is expressed in binomial form as:

(13)

Thus, and as in [19] and [20] , respectively. For k = 4,

coincides with one form of Raney numbers as mentioned above, i.e.,. The numbers generate a lot of new sequences. For example, the sequence of, i.e.,

is not found in the OEIS database [6] .

From theorem (2), one can get

This formula can be also obtained easily by a different way:

1) Count the number of trees by joining the 2 copies of tree, with total number of vertices.

2) Subtract those trees remunerate from but doesn’t contain, that is, exactly the number.

Let the generating function of be. Then we have the following result.

Corollary 5. For and, the generating function, is

(14)

where is the generating function of.

Corollary 6. For,

(15)

or

(16)

Using the binomial inequality in [21] and the binomial forms of and, the following in- equality can be easily proved.

Corollary 7. For,

(17)

where and.

For sufficiently large, a simpler form is produced as well, i.e.,. These results are conjectured in a weaker form in [20] , i.e.,.

4. Catalan Triangle

A Catalan triangle is defined as follows [9] :

The Catalan triangle satisfies [9] :

(18)

Using a property of Catalan numbers, , where, we get another

form of, i.e.,

(19)

where. From Equation (1), we immediately recover the Catalan triangle from the Raney numbers, i.e.,:

(20)

We now consider the following problem as in [22] : Find out the number of all different connected sub-trees of a homogenous binary tree with number of vertices, containing the given number of fixed vertices (where). The condition, , is simply the number of vertices that covers the minimal component containing all vertices. The details of this problem and terminologies could be found in the original paper [22] . We denote the solution to this problem as. In this paper, we show that a solution to the case when the minimal component is “full”, is as below:

where is the number of given vertices and is the number of fixed vertices in each of the connected sub- tree.

Now, we interpret and relate the problem above with the combinatorial interpretation of the Raney numbers through the following steps (see Figure 4):

1) Given vertices;

2) Fill up all the interior points, i.e.,;

3) Fill up all the boundary points, i.e.,;

4) Then only vertices are left;

5) Since each boundary point has 2 neighbours which is not an interior point, we have boxes;

6) If vertices are given, then there are boxes of binary tree to be filled.

As a result, the solution is

(21)

Furthermore, it is natural to define a generalized Catalan triangle, i.e., -th Catalan triangle using Fuss- Catalan numbers instead of Catalan numbers as in Equation (19):

(22)

where if.

From the property of Fuss-Catalan numbers, i.e., corollary (2)

where, we find another form of,

(23)

where. Again, from Equation (1), we immediately have

(24)

Lemma 2. Some properties of -th Catalan triangles are as follows:

(25)

(26)

(27)

Using the binomial form of, one can show that:

Lemma 3. For and

(28)

If, we recover

Based on the initial result, lemma (3), we prove the following assertion by mathematical induction with respect to.

Theorem 3. For fixed, where, and,

(29)

where if.

Proof. Assertion is true for. Assume that it is true for, we consider the following summations:

Hence, the assertion is true for any.

Corollary 8. For fixed, where, and, we have

(30)

For, we have the following simple result:

Corollary 9. For fixed, and,

(31)

where if.

5. Binomial Transformation of k-th Catalan Triangle

For and, we define a new number as:

(32)

If, all the Fuss-Catalan numbers should start at 1, then we recover the previously defined -th Catalan triangle.

From the property of Fuss-Catalan numbers, , where

, we found another form of

(33)

From Equation (1), we immediately have

(34)

and for we recover the same formula for -th Catalan triangle,

From theorem (3), is obtained as a result of binomial transformation of -Catalan triangles.

Corollary 10. For fixed, where, and,

(35)

where if.

6. Conclusion

In this paper, we have introduced the combinatorial interpretation of Raney numbers to solve various tree enumeration counting problems. The upper bound of any order tree enumeration is generally found to be

. We have also shown how a new number may be derived from the binomial transformation

of -th Catalan triangles.

Acknowledgements

This research is funded by the MOHE grant FRGS11-022-0170. The authors are grateful to anoymous referee’s suggestion and improvement of the presentation of this paper.

References