Received 3 July 2014; revised 2 August 2014; accepted 1 September 2014

ABSTRACT

Recently in [1] Goyal and Agarwal interpreted a generalized basic series as a generating function for a colour partition function and a weighted lattice path function. This led to an infinite family of combinatorial identities. Using Frobenius partitions, we in this paper extend the result of [1] and obtain an infinite family of 3-way combinatorial identities. We illustrate by an example that our main result has a potential of yielding Rogers-Ramanujan-MacMahon type identities with convolution property.

Keywords:

Basic Series, Partitions, N-Colour Partitions, Frobenius Partitions, Lattice Paths, Generating Functions, Combinatorial Identities

1. Introduction, Definitions and the Main Results

A series involving factors like rising 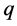-factorial defined by:

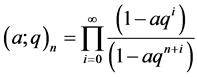
is called basic series (or 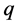-series, or Eulerian series).

Remark: Obviously,

if 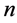is a positive integer.

The following two “sum-product” basic series identities are known as Rogers-Ramanujan identities:

(*)

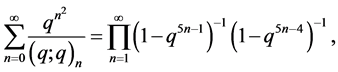and

(**)

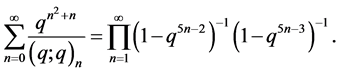They were first discovered by Rogers [2] and rediscovered by Ramanujan in 1913. MacMahon [3] gave the following partition theoretic interpretations of (*) and (**), respectively:

Theorem (*). The number of partitions of 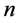into parts with minimal difference 2 equals the number of par- titions of into parts which are congruent to ±1 (mod 5).

Theorem (**). The number of partitions of into parts with minimal part 2 and minimal difference 2 equals the number of partitions of 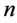into parts which are congruent to ±2 (mod 5).

Partition theoretic interpretations of many more q-series identities like (*) and (**) have been given by several mathematicians (see, for instance, Gӧllnitz [4] [5] , Gordon [6] , Connor [7] , Hirschhorn [8] , Agarwal and Andrews [9] , Subbarao [10] , Subbarao and Agarwal [11] ).

In all these results, ordinary partitions were used. In [12] n-colour partitions were defined. Using these partitions several more basic series identities were interpreted combinatorially (see, for instance, [13] -[17] ). Recently in [1] the basic series,

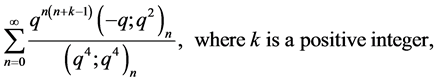
was interpreted as generating function of two different combinatorial objects, viz., an n-colour partition function and a weighted lattice path function. This led to an infinte family of combinatorial identities. Our objective here is to extend the main result of [1] . This gives us an infinite family of 3-way identities which have the potential of yielding many Rogers-Ramanujan-MacMahon type combinatorial identities like Theorems (*)-(**). First we recall the following definitions from [12] :

Definition 1.1 A partition with “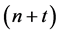copies of n”, (also called an -colour partition), 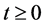, is a partition in which a part of size n, , can occur in different colours denoted by subscripts. For example, the partitions of 2 with “copies of n” are:

Note that zeros are permitted if and only if t is greater than or equal to one.

Definition 1.2 The weighted difference of two elements and, , is defined by and is denoted by.

Definition 1.3 A two-rowed array of non-negative integers,

with each row aligned in non-increasing order is called a generalized Frobenius partition or more simply an F-partition of ν,

if

Next, we recall the following description of lattice paths from [18] which we shall be considering in this paper.

All paths will be of finite length lying in the first quadrant. They will begin on the x-axis or on the y-axis and terminate on the x-axis. Only three moves are allowed at each step:

Northeast: from to,

Southeast: from to, only allowed if,

Horizontal: from to, only allowed along x-axis.

The following terminology will be used in describing lattice paths:

PEAK: Either a vertex on the y-axis which is followed by a southeast step or a vertex preceded by a northeast step and followed by a southeast step.

VALLEY: A vertex preceded by a southeast step and followed by a northeast step. Note that a southeast step followed by a horizontal step followed by a northeast step does not constitute a valley.

MOUNTAIN: A section of the path which starts on either the x- or y-axis, which ends on the x-axis, and which does not touch the x-axis anywhere in between the end points. Every mountain has at least one peak and may have more than one.

PLAIN: A section of the path consisting of only horizontal steps which starts either on y-axis or at a vertex preceded by a southeast step and ends at a vertex followed by a northeast step.

The HEIGHT of a vertex is its y-coordinate. The WEIGHT of a vertex is its x-coordinate. The WEIGHT OF A PATH is the sum of the weights of its peaks.

For the related graphs the reader is referred to the following papers.

(a) T. Mansour, Counting peaks at height k in a Dyck path, Journal of Integer Sequences, 5 (2002), Article 02.1.1.

(b) T. Mansour, Statistics on Dyck paths, Journal of Integer Sequences 9:1 (2006), Article 06.1.5.

(c) P. Peart and W.J. Woan, Dyck paths with no peaks at height k, J. of Integer Sequences 4 (2001), Article 01.1.3.

(d) D. Merlini, R. Sprugnoli and M.C. Verri, Some statistics on Dyck paths, J. Statist. Plann. and Infer. 101 2002, 211-227.

Example: The following path has five peaks, three valleys, three mountains and one plain (Figure 1).

In this example, there are two peaks of height three and three of height two, two valleys of height one and one of height zero.

The weight of this path is.

The following result was proved in [15] .

Theorem 1.1 For a positive integer k, let denote the number of n-colour partitions of ν such that:

(1.1a) the parts are of the form or, if k is an odd and of the form or, if is even

(1.1b) if is the smallest or the only part in the partition, then and

(1.1c) the weighted difference between any two consecutive parts is nonnegative and is.

Let denote the number of lattice paths of weight ν which start at, such that,

(1.1d) they have no valley above height 0

(1.1e) there is a plain of length in the beginning of the path, other plains, if any, are of lengths which are multiples of 4 and

(1.1f) the height of each peak of odd (resp., even) weight is 1 (resp. 2) if k is odd and 2 (resp. 1) if k is even. Then

(1.1)

and

(1.2)

In this paper we propose to prove the following theorems which extend Theorem 1.1 for odd and even k separately:

Theorem 1.2 For k an odd positive integer, let denote the number of F-partitions of ν such that:

(1.2a)

(1.2b)

(1.2c) and,

(1.2d) and

As in Theorem 1.1, let denote the number of n-colour partitions of ν such that:

(1.2e) the parts are,

(1.2f) only the first copy of the odd parts and the second copy of the even parts are used, that is, the parts are of the form or,

(1.2g) if is the smallest or the only part in the partition, then, and,

(1.2h) the weighted difference of any two consecutive parts is non-negative and is.

Then

Theorem 1.3 For k an even positive integer, let denote the number of F-partitions of ν such that:

(1.3a)

(1.3b)

(1.3c) and,

(1.3d) and

As in Theorem 1.1, let denote the number of n-colour partitions of ν such that:

(1.3e) the parts are,

(1.3f) only the second copy of the odd parts and the first copy of the even parts are used, that is, the parts are of the form or,

(1.3g) if is the smallest or only part in the partition, then,

(1.3h) the weighted difference of any two consecutive parts is non-negative and is.

Then

In our next section we give the detailed proof of Theorem 1.2. The proofs of Theorem 1.2 and Theorem 1.3 are similar and hence the proof of Theorem 1.3 is omitted. The interested reader can supply it or obtain from the authors. In Section 3 we illustrate by an example that our results have the potential of yielding Rogers- Ramanujan-MacMahon type combinatorial identities.

2. Proof of Theorem 1.2

We establish a one-one correspondence between the F-partitions enumerated by and n-colour partitions

enumerated by. We do this by mapping each column of F-partitions to a single part of n-

colour partition. The mapping is:

(2.1)

and the inverse mapping is given by:

(2.2)

Clearly (2.1) and (1.2a) imply (1.2e). Also (2.1) and (1.2b) imply (1.2f). Since is the smallest part of the n-colour partition, we see that (2.1) and (1.2c) imply (1.2g). Now suppose and. Then since and, we have

which is non-negative and is divisible by 4 in view of (1.2d) and so (1.2h) follows.

To see the reverse implication we note that (2.2) and (1.2e) imply (1.2a).

(2.2) and (1.2f) imply (1.2b). Since if is the smallest part then, we see that (2.2) and (1.2g) imply (1.2c).

Now suppose, are two consecutive parts in an n-colour partition with and

Then in view of (2.2.),we have

(2.3)

Clearly (2.3) and (1.2h) imply (1.2d).

This completes the proof of Theorem 1.2.

To illustrate the bijection we have constructed, we give an example for shown in Table 1.

Thus

3. A Particular Case

By a little series manipulation, the following identity of Slater [19] (Equation (25)):

(3.1)

can be written in the following form:

(3.2)

Now an appeal to Theorem 1.1 gives the following 3-way combinatorial interpretation of Identity (3.2)

Theorem 3.1: Let denote the number of partitions of ν into parts. Let denote the number of partitions of ν into parts. Then

(3.3)

where and are as defined in Theorem 1.1.

Example.

Also

For, Table 2 shows the relevant partitions enumerated by, and and Table 3 shows the relevant lattice paths enumerated by.

Our Theorem 1.2 provides a four way extension of (3.3) as follows:

(3.4)

Table 4 gives the relevant F-partitions enumerated by for.

4. Conclusion

The work done in this paper shows a nice interaction between the theory of basic series and combinatorics. Theorems 1.1, 1.2 and 1.3 give a 3-way combinatorial identity for each value of k. Thus we get infinitely many 3-way combinatorial identities from these theorems. In one particular case, viz., we get a 4-way com- binatorial interpretation of one well known basic series identity of L. J. Slater.

It would be of interest if more applications of Theorems 1.1, 1.2 and 1.3 can be found.

References

NOTES

^*Supported by CSIR Research Grant No. 09/135(0636)/2011-EMR-I.

^#Emeritus Scientist CSIR, Research Grant No. 21(0879)/11/EMR-II.