Open Journal of Discrete Mathematics
Vol.4 No.2(2014), Article ID:44688,9 pages DOI:10.4236/ojdm.2014.42004
General Cyclic Orthogonal Double Covers of Finite Regular Circulant Graphs
Ramadan El-Shanawany, Hanan Shabana
Department of Physics and Engineering Mathematics, Faculty of Electronic Engineering, Menoufiya University, Menouf, Egypt
Email: ramadan_elshanawany380@yahoo.com, the_engineer_hanan@yahoo
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 20 January 2014; revised 18 February 2014; accepted 15 March 2014
ABSTRACT
An orthogonal double cover (ODC) of a graph H is a collection 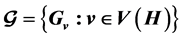 of
of 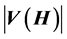 subgraphs (pages) of H, so that they cover every edge of H twice and the intersection of any two of them contains exactly one edge. An ODC
subgraphs (pages) of H, so that they cover every edge of H twice and the intersection of any two of them contains exactly one edge. An ODC  of H is cyclic (CODC) if the cyclic group of order
of H is cyclic (CODC) if the cyclic group of order 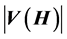 is a subgroup of the automorphism group of
is a subgroup of the automorphism group of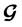 . In this paper, we introduce a general orthogonal labelling for CODC of circulant graphs and construct CODC by certain classes of graphs such as complete bipartite graph, the union of the co-cycles graph with a star, the center vertex of which, belongs to the co-cycles graph and graphs that are connected by a one vertex.
. In this paper, we introduce a general orthogonal labelling for CODC of circulant graphs and construct CODC by certain classes of graphs such as complete bipartite graph, the union of the co-cycles graph with a star, the center vertex of which, belongs to the co-cycles graph and graphs that are connected by a one vertex.
Keywords:Graph Decomposition, Cyclic Orthogonal Double Cover, Automorphism Group, Orthogonal Labelling

1. Introduction
All graphs we deal with are undirected, finite and simple. Let 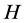 be any regular graph, and let
be any regular graph, and let 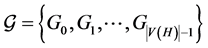 be a collection of
be a collection of 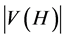 subgraphs (pages) of
subgraphs (pages) of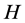 . The collection
. The collection  is an orthogonal double cover (ODC) of
is an orthogonal double cover (ODC) of  if it has the following properties:
if it has the following properties:
1) Double cover property:
Every edge of  is contained in exactly two of the pages in
is contained in exactly two of the pages in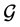 .
.
2) Orthogonality property:
For any two distinct pages 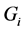 and
and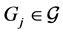 ,
, 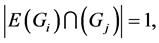 if and only if i and j are adjacent in
if and only if i and j are adjacent in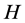 .
.
If all pages 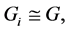 for all
for all  then
then  is an ODC of
is an ODC of 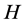 by
by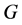 . An automorphism of an ODC
. An automorphism of an ODC 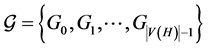 of
of  is a permutation
is a permutation 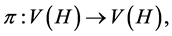 such that
such that 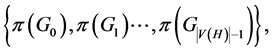 where for
where for 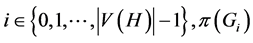 is a subgraph of
is a subgraph of 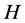 with
with 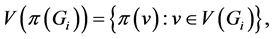 and
and 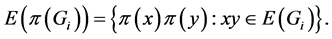 According to the obvious properties of ODCs by a graph
According to the obvious properties of ODCs by a graph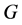 , the underlying graph H has to be
, the underlying graph H has to be 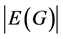 -regular. This concept is a generalization of the definitions of an ODC of complete graphs and complete bipartite graphs, which has been studied extensively [1] -[2] . El-Shanawny et al. studied extensively the ODC of complete bipartite graphs; see [3] -[6] . An effective method to construct ODCs in the above cases was based on the idea of translate a given subgraph
-regular. This concept is a generalization of the definitions of an ODC of complete graphs and complete bipartite graphs, which has been studied extensively [1] -[2] . El-Shanawny et al. studied extensively the ODC of complete bipartite graphs; see [3] -[6] . An effective method to construct ODCs in the above cases was based on the idea of translate a given subgraph 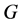 by a group acting on
by a group acting on  If the cyclic group of order
If the cyclic group of order  is a subgroup of the automorphism group of
is a subgroup of the automorphism group of 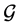 (the set of all automorphisms of
(the set of all automorphisms of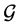 ), then an ODC
), then an ODC  of
of  is cyclic (CODC). Therefore, the circulant graph is of special interest. In [7] , Scapellato et al. offers some insights on the case on ODC of Cayley graphs on cyclic groups. In [8] , Hartmann and Schumacher proved the following: 1) Let
is cyclic (CODC). Therefore, the circulant graph is of special interest. In [7] , Scapellato et al. offers some insights on the case on ODC of Cayley graphs on cyclic groups. In [8] , Hartmann and Schumacher proved the following: 1) Let 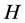 be a 2-regular graph. There exists an ODC of
be a 2-regular graph. There exists an ODC of 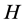 by
by 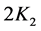 with three exceptions for
with three exceptions for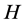 :
: 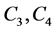 and
and , 2) Let
, 2) Let 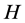 be a 3-regular graph containing a 1-factor and without a component isomorphic to
be a 3-regular graph containing a 1-factor and without a component isomorphic to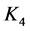 . There exists an ODC of
. There exists an ODC of 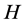 by
by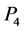 , 3) Let
, 3) Let 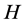 be a 3-regular graph containing a 1-factor and
be a 3-regular graph containing a 1-factor and . There exists an ODC of
. There exists an ODC of 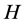 by
by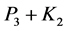 . In [9] , Sampathkumar et al. introduced a special kind of orthogonal labelling called orthogonal σ-labelling, and they found it for some caterpillars of diameters 4. In [7] , Scapellato et al. studied the ODC of Cayley graphs and proved the following: 1) All 3-regular Cayley graphs, except
. In [9] , Sampathkumar et al. introduced a special kind of orthogonal labelling called orthogonal σ-labelling, and they found it for some caterpillars of diameters 4. In [7] , Scapellato et al. studied the ODC of Cayley graphs and proved the following: 1) All 3-regular Cayley graphs, except , have ODCs by
, have ODCs by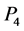 , 2) All 3-regular Cayley graphs on Abelian groups, except
, 2) All 3-regular Cayley graphs on Abelian groups, except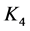 , have ODCs by
, have ODCs by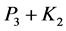 3) All 3-regular Cayley graphs on Abelian groups, except
3) All 3-regular Cayley graphs on Abelian groups, except 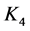 and the
and the 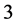 - prism (Cartesian product of
- prism (Cartesian product of 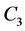 and
and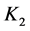 ), have ODCs by
), have ODCs by 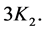 In [10] , Sampathkumar et al. completely settled the existence problem of CODCs of 4-regular circulant graphs.
In [10] , Sampathkumar et al. completely settled the existence problem of CODCs of 4-regular circulant graphs.
The above results on ODCs of graphs with lower degrees motivate us to consider CODCs of graphs with higher degrees. In [11] , El-Shanawny et al. deal with cayley graphs on abelian groups and proved the existence of ODCs of cayley graphs by several classes of graphs. Here we are concerned with CODCs of circulant graphs of finite degrees higher than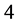 . The paper is organized as follows, Section 1.1 describes the method that can be used throughout. Section-2 constructs CODCs of circulant graphs of finite degrees higher than
. The paper is organized as follows, Section 1.1 describes the method that can be used throughout. Section-2 constructs CODCs of circulant graphs of finite degrees higher than  by certain graph classes. Section 3 offers the general CODCs of circulant graphs.
by certain graph classes. Section 3 offers the general CODCs of circulant graphs.
Definition 1. For a sequence 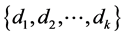 of positive integers with
of positive integers with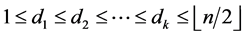 , the circulant graph
, the circulant graph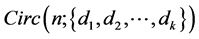 , has vertex set
, has vertex set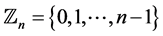 ; two vertices
; two vertices  and
and  are adjacent, if and only if
are adjacent, if and only if  for some
for some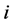 ,
, 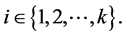
For an edge 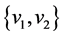 in
in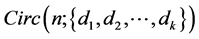 , the length of
, the length of 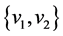 is
is  Given two edges
Given two edges 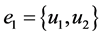 and
and 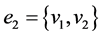 of the same length
of the same length 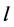 in
in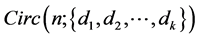 , the rotation distance
, the rotation distance 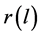 between
between  and
and 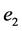 is
is 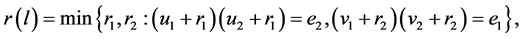 where addition and difference are calculated inside
where addition and difference are calculated inside 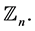 Note that if
Note that if 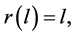 then the edges
then the edges  and
and  are adjacent; if
are adjacent; if 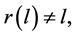 then the edges
then the edges 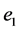 and
and  are non adjacent.
are non adjacent.
Throughout the paper we make use of the usual notation: 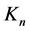 for the complete graph on
for the complete graph on 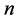 vertices,
vertices, 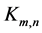 for the complete bipartite graph with independent sets of sizes
for the complete bipartite graph with independent sets of sizes 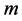 and
and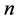 ,
,  for the path on
for the path on 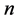 vertices,
vertices, 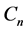 for the cycle on
for the cycle on 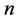 vertices,
vertices,  for the disjoint union
for the disjoint union 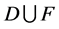 of
of  and
and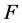 ,
, 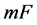 for
for  disjoint copies of
disjoint copies of 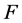 and
and 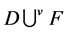 for the union of
for the union of 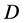 and
and 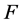 with a common vertex
with a common vertex 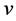 belongs to
belongs to 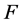 and
and 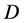 Let
Let 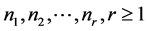 be positive integers,
be positive integers, 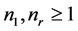 and
and  for
for  the caterpillar
the caterpillar
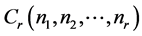 is the tree obtained from the path
is the tree obtained from the path 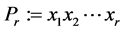 by joining vertex
by joining vertex 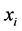 to
to 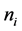 new vertices,
new vertices, 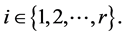 Other terminology not defined here can be found in [12] .
Other terminology not defined here can be found in [12] .
CODC of Circulant Graphs
Consider the complete graph 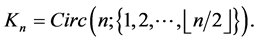 The authors of [13] introduced the notion of an orthogonal labelling. Given a graph
The authors of [13] introduced the notion of an orthogonal labelling. Given a graph 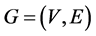 with
with 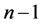 edges, a
edges, a 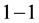 mapping
mapping 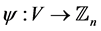 is an orthogonal labelling of
is an orthogonal labelling of  if the following conditions are satisfied:
if the following conditions are satisfied:
1) For every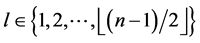 ,
,  contains exactly two edges of length
contains exactly two edges of length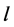 , and exactly one edge of length
, and exactly one edge of length  if
if 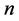 is even, and 2) For every
is even, and 2) For every 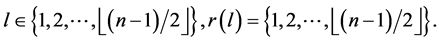
The following theorem of Gronau et al. [13] relates CODCs of 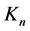 and orthogonal labellings.
and orthogonal labellings.
Theorem 2. ([13] ) A CODC of  by a graph
by a graph 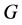 exists if and only if there exists an orthogonal labelling of
exists if and only if there exists an orthogonal labelling of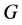 .
.
Sampathkumar and Srinivasan [10] , called an orthogonal 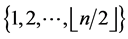 -labelling and generalized it to an orthogonal
-labelling and generalized it to an orthogonal 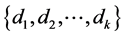 -labelling, where
-labelling, where 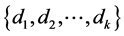 is a sequence of positive integers with
is a sequence of positive integers with  .
.
1) Either n is odd or even and 
Given a subgraph 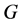 of
of 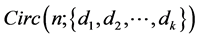 with
with 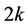 edges, a labelling of
edges, a labelling of  in
in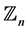 , is an orthogonal
, is an orthogonal 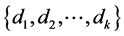 -labelling of
-labelling of 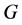 if:
if:
a) For every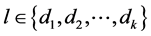 ,
, 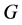 contains exactly two edges of length
contains exactly two edges of length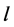 , and b)
, and b) 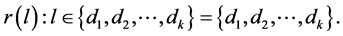
2) 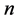 is even and
is even and 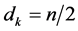
Given a subgraph  of
of  with
with 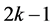 edges, a labelling of
edges, a labelling of  in
in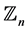 , is an orthogonal
, is an orthogonal 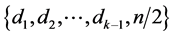 -labelling of
-labelling of 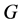 if:
if:
a) For every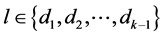 ,
, 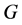 contains exactly two edges of length
contains exactly two edges of length , and
, and  contains exactly one edges of length
contains exactly one edges of length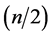 , and b)
, and b) , The following theorem of Sampathkumar and Simaringa [10] , is a generalization of Theorem 2.
, The following theorem of Sampathkumar and Simaringa [10] , is a generalization of Theorem 2.
Theorem 3 ([10] ). A CODC of 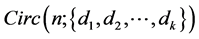 by a graph
by a graph  exists, if and only if there exists an orthogonal
exists, if and only if there exists an orthogonal 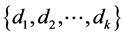 -labelling of
-labelling of 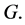
2. CODCs of Circulant Graphs by Certain Graph Classes
This section is devoted to constructing the cyclic orthogonal double covers (CODCs) of circulant graphs by different classes of graphs, complete bipartite graph as in Section 2.1, the union of the co-cycles graph with a star, the center vertex of which, belongs to the co-cycles graph as in Section 2.2 and graphs that are connected by a one vertex as in Section 2.3.
2.1. CODCs by a Complete Bipartite Graph
Theorem 4. For any positive integers 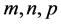 such that
such that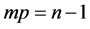 , there exists a CODC of
, there exists a CODC of 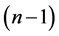 -regular
-regular 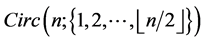 by
by .
.
Proof Let us define 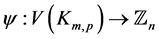 by
by  for
for 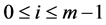 and
and  for
for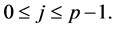 Then the edges of length
Then the edges of length 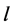 where
where 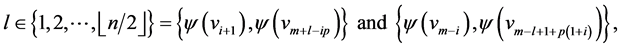 where
where 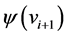 is defined for
is defined for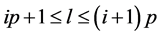 . For every
. For every 
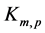 contains exactly two edges of length
contains exactly two edges of length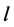 , and
, and 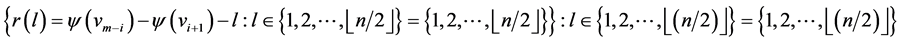 , and hence
, and hence 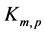 has an orthogonal labelling. By Theorem 3, there exists a CODC Of
has an orthogonal labelling. By Theorem 3, there exists a CODC Of 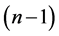 -regular
-regular 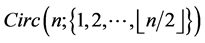 by
by .
.
Let us define 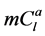 to be the co-cycles graph (the union of
to be the co-cycles graph (the union of 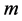 cycles of length
cycles of length 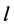 with a one vertex
with a one vertex  in common). In the following section we construct a CODCs of finite regular circulant graphs by
in common). In the following section we construct a CODCs of finite regular circulant graphs by 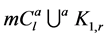 (the union of co-cycles graph with a star whose center vertex is the vertex
(the union of co-cycles graph with a star whose center vertex is the vertex ).
).
2.2. CODCs of Circulant Graph by 
Theorem 5 For any positive integer 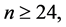 there exists a CODC of
there exists a CODC of  -regular
-regular 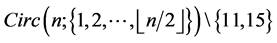 by
by 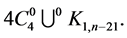
Proof Let us define 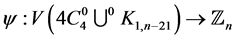 by
by 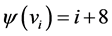 for
for 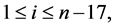 where,
where, 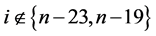 ,
,  ,
,  ,
, 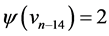 ,
, 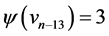 ,
, 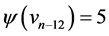 ,
, 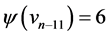 ,
, 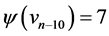 ,
, 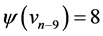 ,
, 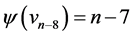 ,
,  and
and . Then the edges of length
. Then the edges of length  are
are  and
and ; those of length
; those of length 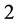 are
are 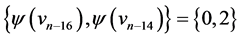 and
and 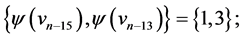 those of length
those of length 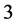 are
are 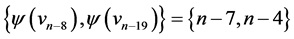 and
and  those of length
those of length 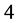 are
are 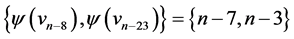 and
and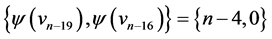 ; those of length
; those of length  are
are 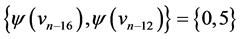 and
and 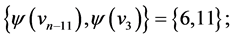 those of length
those of length 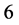 are
are 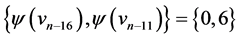 and
and 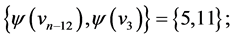 those of length
those of length  are
are 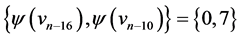 and
and 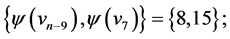 those of length 8 are
those of length 8 are 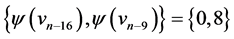 and
and  the edges of length l where
the edges of length l where  are
are 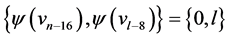 and
and 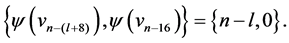 For every
For every 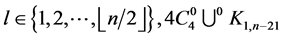 contains exactly two edges of length
contains exactly two edges of length 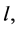 and
and 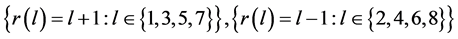 and then
and then 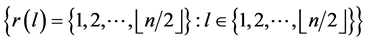 and hence
and hence  has an orthogonal labelling. By Theorem 3, there exists a CODC of
has an orthogonal labelling. By Theorem 3, there exists a CODC of  -regular
-regular  by
by 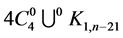 for
for  ‚
‚
Theorem 6 For any positive integer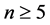 , there exists a CODC of
, there exists a CODC of 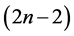 -regular
-regular  by
by .
.
Proof Let us define 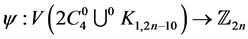 by
by 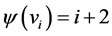 for
for 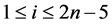 where
where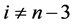 ,
,  ,
, 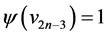 and
and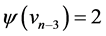 . Then the edges of length
. Then the edges of length 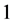 are
are 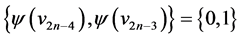 and
and  those of length
those of length 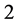 are
are 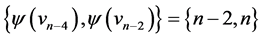 and
and  ; those of length
; those of length 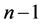 are
are  and
and 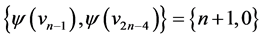 the edges of length
the edges of length  where
where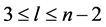 are
are 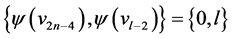 and
and . For every
. For every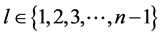 ,
, 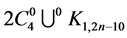 contains exactly two edges of length
contains exactly two edges of length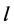 , and since every two edges of the same length are adjacent then
, and since every two edges of the same length are adjacent then 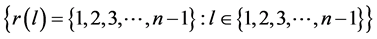 and hence
and hence 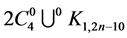 has an orthogonal labelling. By Theorem 3, there exists a CODC of
has an orthogonal labelling. By Theorem 3, there exists a CODC of 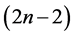 -regular
-regular 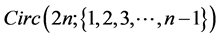 by
by 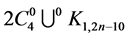 for
for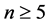 . ‚
. ‚
Theorem 7 For any positive integer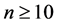 , there exists a CODC of
, there exists a CODC of 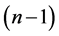 -regular
-regular 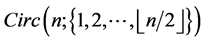 by
by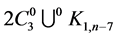 .
.
Proof Let us define 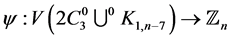 by
by 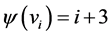 for
for ,
, 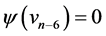 ,
, 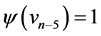 ,
, 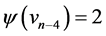 ,
, 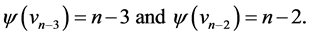 Then the edges of length
Then the edges of length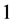 are
are  and
and 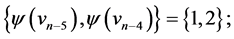 those of length
those of length 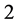 are
are 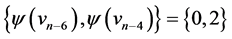 and
and 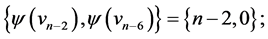 those of length 3 are
those of length 3 are  and
and  the edges of length
the edges of length 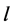 where
where 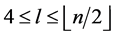 are
are  and
and  For every
For every 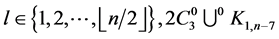 contains exactly two edges of length
contains exactly two edges of length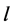 , and since every two edges of the same length are adjacent then
, and since every two edges of the same length are adjacent then 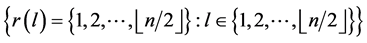 and hence
and hence  has an orthogonal labelling. By Theorem 3, there exists a CODC of
has an orthogonal labelling. By Theorem 3, there exists a CODC of 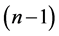 -regular
-regular 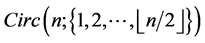 by
by 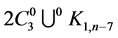 for
for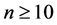 . ‚
. ‚
Theorem 8 For any positive integer 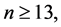 there exists a CODC of
there exists a CODC of 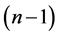 -regular
-regular 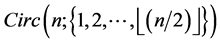 by
by .
.
Proof Let us define 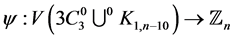 by
by 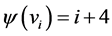 for
for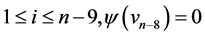 ,
,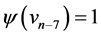 ,
, 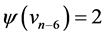 ,
, 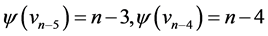 and
and 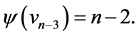 Then the edges of length
Then the edges of length 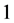 are
are 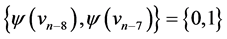 and
and 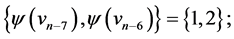 those of length
those of length 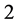 are
are 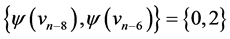 and
and 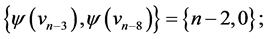 those of length
those of length 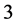 are
are 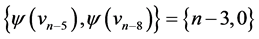 and
and 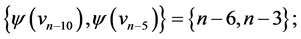 those of length
those of length 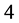 are
are 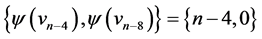 and
and 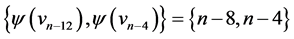 the edges of length
the edges of length  where
where  are
are  and
and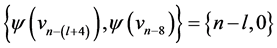 . For every
. For every 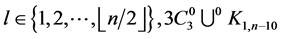 contains exactly two edges of length
contains exactly two edges of length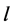 , and since every two edges of the same length are adjacent then
, and since every two edges of the same length are adjacent then 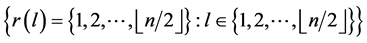 and hence
and hence 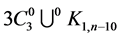 has an orthogonal labelling. By Theorem 3, there exists a CODC of
has an orthogonal labelling. By Theorem 3, there exists a CODC of 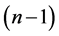 -regular
-regular  by
by  for
for . ‚
. ‚
Theorem 9 For any positive integer 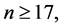 there exists a CODC of
there exists a CODC of 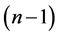 -regular
-regular  by
by .
.
Proof Let us define 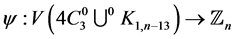 by
by  for
for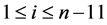 ,
, 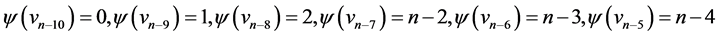 , and
, and . Then the edges of length
. Then the edges of length 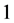 are
are 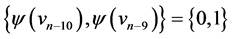 and
and 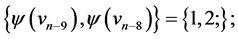 those of length
those of length 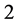 are
are 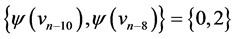 and
and 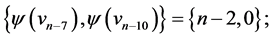 those of length
those of length  are
are  and
and 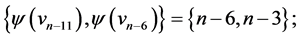 those of length
those of length 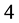 are
are 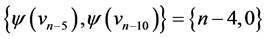 and
and 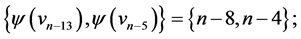 those of length
those of length 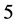 are
are 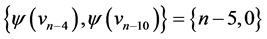 and
and 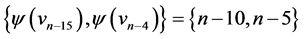 the edges of length
the edges of length 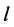 where
where  are
are 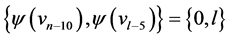 and
and 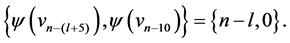 For every
For every 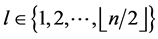 ,
,  contains exactly two edges of length
contains exactly two edges of length , and since every two edges of the same length are adjacent then
, and since every two edges of the same length are adjacent then 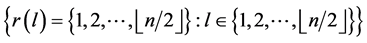 and hence
and hence  has an orthogonal labelling. By theorem 3, there exists a CODC of
has an orthogonal labelling. By theorem 3, there exists a CODC of 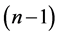 -regular
-regular 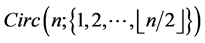 by
by 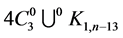 for
for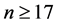 . ‚
. ‚
According to these results, we can pose the following conjecture:
Conjecture 1. For any positive integers  such that
such that 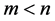 and
and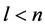 , there exists a CODC of
, there exists a CODC of 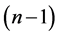 -regular
-regular 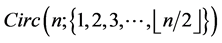 by
by .
.
2.3. CODCs by 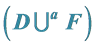 Graphs that Are Connected by a One Vertex a
Graphs that Are Connected by a One Vertex a
Theorem 10 For any positive integer  there exists a CODC of
there exists a CODC of 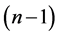 -regular
-regular 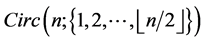 by
by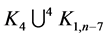 .
.
Proof Let us define 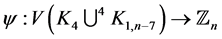 by
by 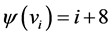 for
for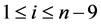 ,
,  ,
,  ,
, 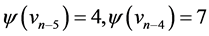 and
and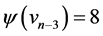 . Then the edges of length
. Then the edges of length 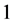 are
are 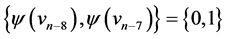 and
and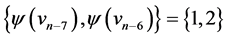 ; those of length
; those of length 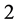 are
are 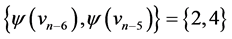 and
and ; those of length
; those of length 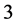 are
are 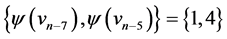 and
and 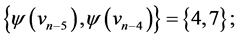 those of length
those of length 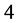 are
are  and
and 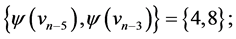 the edges of length
the edges of length 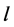 where
where 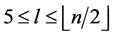 are
are 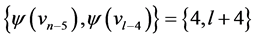 and
and  For every
For every 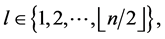
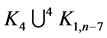 contains exactly two edges of length
contains exactly two edges of length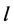 , and since every two edges of the same length are adjacent then
, and since every two edges of the same length are adjacent then 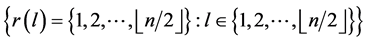 and hence
and hence 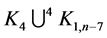 has an orthogonal labelling. By Theorem 3, there exists a CODC of
has an orthogonal labelling. By Theorem 3, there exists a CODC of 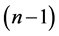 -regular
-regular 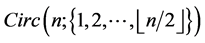 by
by 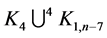 for
for . ‚
. ‚
Theorem 11 For any prime number 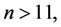 there exists a CODC of
there exists a CODC of 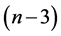 -regular
-regular  by
by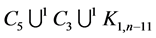 .
.
Proof Let us define 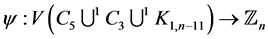 by
by 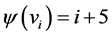 for
for ,
, 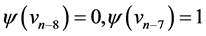 ,
, 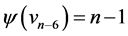 ,
, 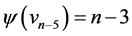 and
and . Then the edges of length
. Then the edges of length 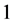 are
are  and
and  those of length
those of length  are
are  and
and ; those of length
; those of length  are
are 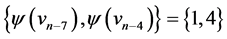 and
and  the edges of length
the edges of length 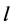 where
where 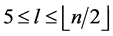 are
are 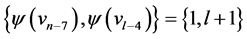 and
and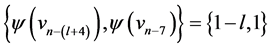 . For every
. For every 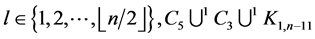 contains exactly two edges of length
contains exactly two edges of length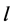 , and since every two edges of the same length are adjacent then
, and since every two edges of the same length are adjacent then 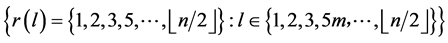 and hence
and hence 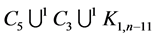 has an orthogonal labelling. By Theorem 3, there exists a CODC of
has an orthogonal labelling. By Theorem 3, there exists a CODC of 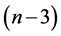 -regular
-regular 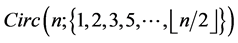 by
by 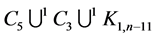 for
for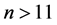 . ‚
. ‚
Theorem 12 For any positive integer  there exists a CODC of
there exists a CODC of 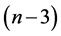 -regular
-regular
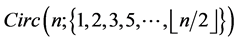 by
by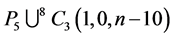 .
.
Proof Let us define  by
by 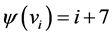 for
for ,
,  ,
, 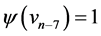 ,
, 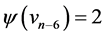 ,
, 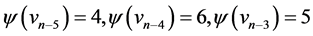 and
and 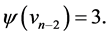 Then the edges of length
Then the edges of length  are
are  and
and 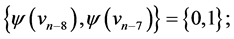 those of length
those of length 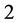 are
are  and
and 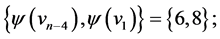 those of length
those of length 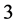 are
are 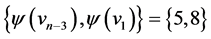 and
and 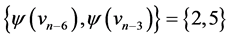 the edges of length
the edges of length  where
where 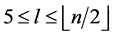 are
are 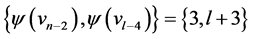 and
and 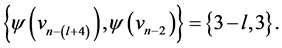 For every
For every  contains exactly two edges of length
contains exactly two edges of length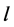 , and since every two edges of the same length are adjacent then
, and since every two edges of the same length are adjacent then  and hence
and hence  has an orthogonal labelling. By Theorem 3, there exists a CODC of
has an orthogonal labelling. By Theorem 3, there exists a CODC of  -regular
-regular 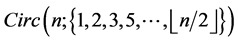 by
by 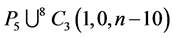 for
for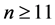 . ‚
. ‚
Conjecture 2. For any positive integers  so that
so that , there exists a CODC of
, there exists a CODC of 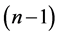 -regular
-regular 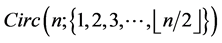 by
by .
.
3. General CODCs of Circulant Graph
In constructing CODCs a natural approach is to try to use given CODCs to obtain CODCs of a larger Circulant Graph. That is we will do in the following theorem.
Theorem 13 For any positive integers 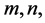 if there exists a CODC of
if there exists a CODC of  by G with respect to
by G with respect to 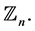 Then there exists a CODC of
Then there exists a CODC of  where
where 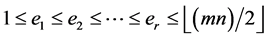 by
by  with respect to
with respect to .
.
Proof Let the  has a CODC by
has a CODC by 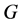 with respect to
with respect to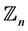 . Then the graph
. Then the graph 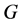 has an orthogonal
has an orthogonal 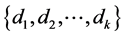 -labelling with respect to
-labelling with respect to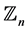 . And hence, for every
. And hence, for every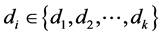 ,
, 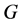 contain exactly two edges of the length
contain exactly two edges of the length  as
as 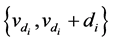 and
and  where
where 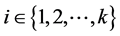 and
and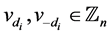 . And
. And  to construct a CODC of
to construct a CODC of 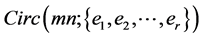 for
for 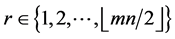 by
by 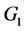 with respect to
with respect to , the graph
, the graph 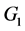 must have an orthogonal
must have an orthogonal 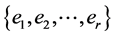 -labelling with respect to
-labelling with respect to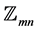 . From the orthogonal labelling of
. From the orthogonal labelling of 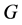 we can obtain an orthogonal labelling of
we can obtain an orthogonal labelling of  as follows Case 1: Either
as follows Case 1: Either 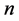 is odd or even and
is odd or even and 
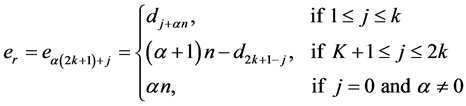
where 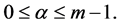 For every
For every 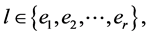
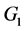 contain exactly two edges of the length
contain exactly two edges of the length  as
as 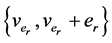 and
and 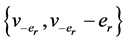 where
where
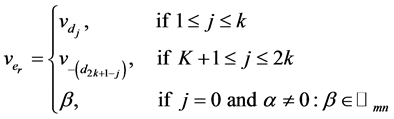
and
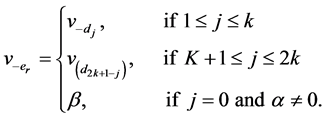
By the definition of ,
, and
and , we have
, we have 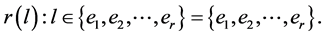 Then the graph
Then the graph 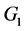 has an orthogonal
has an orthogonal 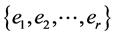 -labelling with respect to
-labelling with respect to .
.
Case 2:  is even and
is even and 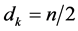
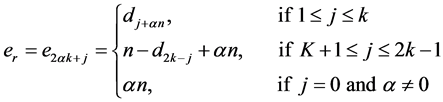
where . For every
. For every ,
,  contain exactly two edges of the length
contain exactly two edges of the length  as
as  and
and  where
where
and
By the definition of, ,
,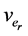 and
and , we have
, we have 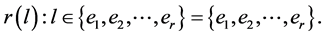 Then the graph
Then the graph 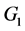 has an orthogonal
has an orthogonal 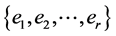 -labelling with respect to
-labelling with respect to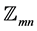 . By Theorem 3, there exists a CODC of
. By Theorem 3, there exists a CODC of 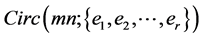 by
by 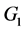 with respect to
with respect to .
.
4. Conclusion
In this paper we are concerned with the orthogonal labelling of CODCs of finite regular circulant graphs. We constructed CODCs by certain classes of graphs such as complete bipartite graph, the union of the co-cycles graph with a star, the center vertex of which belongs to the co-cycles graph and graphs that are connected by a one vertex. Finally we introduced general CODCs of the circulant graph.
References
- Gronau, H.-D.O.F., Hartmann, S., Grüttmüller, M., Leck, U. and Leck, V. (2002) On Orthogonal Double Covers of Graphs. Design Codes Cryptography, 27, 49-91. http://dx.doi.org/10.1023/A:1016546402248
- El-Shanawany, R. and Higazy, M. (2008) Orthogonal Double Covers of Complete Graphs by Certain Spanning Subgraphs. Australasian Journal of Combinatorics, 42, 223-228.
- El Shanawany, R., Higazy, M. and Scapellato, R. (2010) A Note on Orthogonal Double Covers of Complete Bipartite Graphs by a Special Class of Six Caterpillars. AKCE International Journal of Graphs and Combinatorics, 7, 1-4.
- El-Shanawany, R.A., Higazy, M.S. and Scapellato, R. (2009) Orthogonal Double Covers of Complete Bipartite Graphs by the Union of a Cycle and a Star. Australasian Journal of Combinatorics, 43, 281-293.
- El-Shanawany, R. and Higazy, M. (2007) General Symmetric Starter of Orthogonal Double Covers of Complete Bipartite Graph. International Journal of Mathematics and Mathematical Sciences, 2007, Article ID: 42892. http://dx.doi.org/10.1155/2007/42892
- El Shanawany, R., Higazy, M. and El Mesady, A. (2013) On Cartesian Products of Orthogonal Double Covers. International Journal of Mathematics and Mathematical Sciences, 2013, Article ID: 265136.
- Scapellato, R., El-Shanawany, R. and Higazy, M. (2009) Orthogonal Double Covers of Cayley Graphs. Discrete Applied Mathematics, 157, 3111-3118. http://dx.doi.org/10.1016/j.dam.2009.06.005
- Hartmann, S. and Schumacher, U. (2004) Orthogonal Double Covers of General Graphs. Discrete Applied Mathematics, 138, 107-116. http://dx.doi.org/10.1016/S0166-218X(03)00274-9
- Sampathkumar, R. and Sriram, V. (2008) Orthogonal σ-Labelling of Graphs. AKCE International Journal of Graphs and Combinatorics, 5, 57-60.
- Sampathkumar, R. and Srinivasan, S. (2011) Cyclic Orthogonal Double Covers of 4-Regular Circulant Graphs. Discrete Mathematics, 311, 2417-2422. http://dx.doi.org/10.1016/j.disc.2011.06.021
- El Shanawany, R., and Shabana, H. (2014) On Orthogonal Double Covers of Circulant Graphs. British Journal of Mathematics & Computer Science, 4, 394-401.
- Balakrishnan, R. and Ranganathan, K. (2012) A Textbook of Graph Theory. Springer, Berlin. http://dx.doi.org/10.1007/978-1-4614-4529-6
- Gronau, H.-D.O.F., Mullin, R.C. and Rosa, A. (1997) On Orthogonal Double Covers of Complete Graphs by Trees. Graphs and Combinatorics, 13, 251-262.

