Open Journal of Discrete Mathematics
Vol.4 No.1(2014), Article ID:42400,5 pages DOI:10.4236/ojdm.2014.41001
On a Sufficient and Necessary Condition for Graph Coloring
Maodong Ye
Department of Mathematics, Zhejiang University, Hangzhou, China
Email: ymd@css.zju.edu.cn
Copyright © 2014 Maodong Ye. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Maodong Ye. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received August 5, 2013; revised September 3, 2013; accepted October 2, 2013
ABSTRACT
Using the linear space over the binary field that related to a graph G, a sufficient and necessary condition for the chromatic number of G is obtained.
Keywords: Vertex Coloring; Chromatic Number; Outer-Kernel Subspace; Plane Graph
1. Introduction
Let  be a graph, where V is a set of vertices and E is a set of edges of G. A vertex coloring of a graph G is a coloring to all the vertices of G with p colors so that no two adjacent vertices have the same color. Such the graph is called
be a graph, where V is a set of vertices and E is a set of edges of G. A vertex coloring of a graph G is a coloring to all the vertices of G with p colors so that no two adjacent vertices have the same color. Such the graph is called ![]() -coloring. The minimal number p is called the chromatic number of G, and is denoted by
-coloring. The minimal number p is called the chromatic number of G, and is denoted by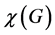 . The so-called Four Color Problem is that for any plane graph G,
. The so-called Four Color Problem is that for any plane graph G, 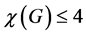 [1].
[1].
The coloring of a graph G is an interesting problem for many people [2]. This is mainly caused by the Four Color Problem [3].
In this paper, putting a graph into a linear space over the binary field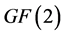 , we obtain the sufficient and necessary condition for the chromatic number of G.
, we obtain the sufficient and necessary condition for the chromatic number of G.
And as an application of above result, we give a characterization for a maximal plane graph to be 4-coloring.
2. The Linear Space An over GF(2)
Now we introduce the linear space over the field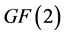 .
.
Firstly, the field 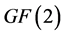 contains only two members:
contains only two members: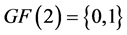 , where the addition and multiplication are as usual excepting that
, where the addition and multiplication are as usual excepting that![]() .
.
Let 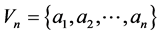 be the n vertices, the all vectors of the linear space
be the n vertices, the all vectors of the linear space  are formed of the symbolic expression
are formed of the symbolic expression
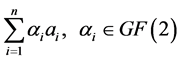 .
.
It has ![]() vectors. The addition of two vectors is defined by
vectors. The addition of two vectors is defined by
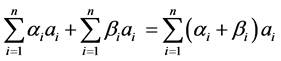 .
.
Here, the 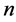 vertices
vertices  will serve as the most basic elements of the linear space
will serve as the most basic elements of the linear space . They will be as a basis of the linear space
. They will be as a basis of the linear space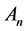 . For them the basic assumption is that these n vertices are linearly independent in
. For them the basic assumption is that these n vertices are linearly independent in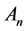 .
.
According to the addition in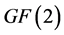 , for any vector
, for any vector 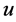 in the linear space
in the linear space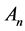 , it has
, it has
![]() .
.
Here we denote the zero vector by 0.
For a vector 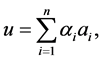 the order of the vector
the order of the vector 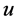 is defined by
is defined by
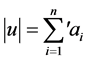 where the
where the  means that the addition is the usual addition in the integer set.
means that the addition is the usual addition in the integer set.
A vector with k order is called a k-order vector, and a vector whose order is even is called an even-order vector.
We now give some structures to the linear space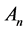 . In other words, we want to “put” a graph into the linear space
. In other words, we want to “put” a graph into the linear space .
.
In the linear space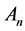 , 1-order vectors are vertices of a graph. The edge is expressed as the 2-order vertex, i.e.
, 1-order vectors are vertices of a graph. The edge is expressed as the 2-order vertex, i.e.  is the edge
is the edge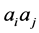 . So we have two ways to describe a edge: by
. So we have two ways to describe a edge: by 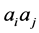 (in the usual sense), or by
(in the usual sense), or by 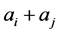 (in the linear space
(in the linear space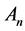 ).
).
In the following, we always discuss a graph in the linear space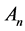 , it means we express edges with the second form.
, it means we express edges with the second form.
All the 2-order vectors in the linear space 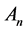 are the all possible edges with
are the all possible edges with 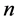 vertices
vertices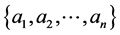 , that we denote by
, that we denote by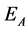 :
:
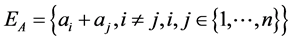 .
.
For a giving graph 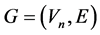 with
with 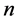 vertices, in the linear space
vertices, in the linear space , the elements of the set
, the elements of the set 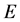 are the 2-order vectors of
are the 2-order vectors of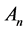 , then the edge set
, then the edge set 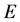 of
of ![]() is the subset of the set
is the subset of the set ,
, .
.
We give two examples here.
1) For the set 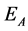 with all the 2-order vertices in
with all the 2-order vertices in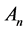 , the graph
, the graph  is a complete graph, whose any two vertices are adjacent.
is a complete graph, whose any two vertices are adjacent.
2) For a graph  with
with 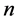 vertices, the complementary set of
vertices, the complementary set of  in the set of the 2-order vertices of
in the set of the 2-order vertices of 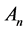 is
is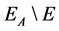 . Then the complementary graph
. Then the complementary graph  of the graph
of the graph ![]() is
is![]() .
.
We now see the addition in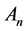 . For a path of
. For a path of ![]() with a sequence of edges
with a sequence of edges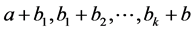 , where the end-points are
, where the end-points are 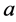 and
and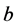 , the sum of the edges is:
, the sum of the edges is:
 .
.
This expression indicates the relation between the addition in the linear space and the connectivity of a graph. That is why we put the graph into the linear space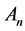 .
.
Lemma 1. The sum of even-order vectors is even-order.
This is clear by the property that  if and only if
if and only if .
.
As a special case of the Lemma 1, we have Lemma 2. Let 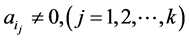 are the vertices of
are the vertices of![]() , if
, if
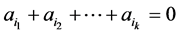 then
then 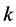 is even.
is even.
Definition. Let An be the n-dimensional linear space derived by the graph 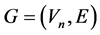 above, and
above, and 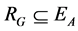 be a set of 2-order vectors. Denote by
be a set of 2-order vectors. Denote by 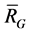 the linear subspace spanned by RG. If there are no edges of E in
the linear subspace spanned by RG. If there are no edges of E in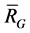 , i.e.
, i.e.
 (1)
(1)
then  is called an outer-kernel subspace of
is called an outer-kernel subspace of![]() . And
. And 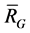 is a maximal outer-kernel subspace if the rank of
is a maximal outer-kernel subspace if the rank of 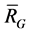 is maxima in all the outer-kernel subspace of
is maxima in all the outer-kernel subspace of![]() .
.
Now we give some basic properties of a outer-kernel subspace of a graph![]() .
.
By definition, 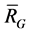 is a subspace of
is a subspace of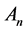 . Denote the set of all 2-order vectors of
. Denote the set of all 2-order vectors of 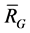 by
by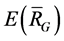 , then
, then
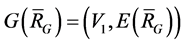 is a subgraph of the complementary graph
is a subgraph of the complementary graph 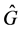 of
of![]() , here
, here  is the 1-order vectors appeared in
is the 1-order vectors appeared in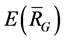 . The subgraph
. The subgraph 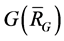 consists of some connected blocks.
consists of some connected blocks.
Lemma 3. Let  be a connected block of
be a connected block of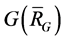 , and
, and 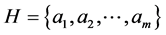 be the vertices of
be the vertices of![]() , then
, then![]() ,
, ![]() is a complete graph
is a complete graph 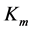 in the
in the 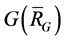 and
and

is the linear subspace of 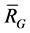
This lemma means that every connected block of 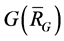 is a complete graph.
is a complete graph.
Proof. Because  is spanned by 2-order vectors, so
is spanned by 2-order vectors, so![]() .
.
Suppose that  for
for  is a linear space , then
is a linear space , then
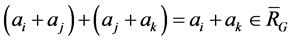 .
.
Since ![]() is connected block of
is connected block of , so
, so . On the other hand, if
. On the other hand, if , then
, then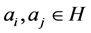 . Hence all the 2-order vectors formed by the set of vertices
. Hence all the 2-order vectors formed by the set of vertices 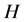 span the linear subspace
span the linear subspace 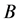 of
of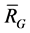 . Thus the connected block
. Thus the connected block ![]() is a complete graph in
is a complete graph in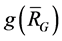 .
.
Lemma 4. If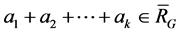 , then
, then 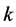 is even and there exists a
is even and there exists a 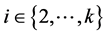 such that
such that .
.
Proof. By the definition of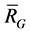 ,
, 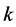 is even. For
is even. For 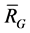 is spanned by 2-order vectors, so
is spanned by 2-order vectors, so  is in a connected block
is in a connected block 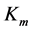 of
of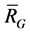 . Thus another vertex
. Thus another vertex 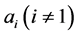 of
of  must appear in
must appear in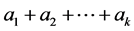 .
.
3. The Main Results
The outer-kernel subspace plays an important role in the problem of vertex coloring.
Theorem 1. Let 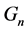 be a graph with n vertices, then the sufficient and necessary condition for
be a graph with n vertices, then the sufficient and necessary condition for  to be p-coloring is that the rank of an outer-kernel subspace
to be p-coloring is that the rank of an outer-kernel subspace 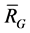 of
of  is
is![]() .
.
Proof. First we prove the necessity. Suppose that the graph  is
is ![]() -coloring. Then all the vertices of
-coloring. Then all the vertices of 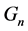 can be divided into
can be divided into ![]() subsets by the colors:
subsets by the colors:
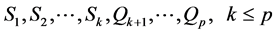 . (2)
. (2)
That means the vertices with a same color are in the same subset. Because it may have a subset with only one vertex, we denote the one-vertex subsets with different colors by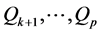 .
.
The elements of subset  are not less then 2. Denote them by
are not less then 2. Denote them by
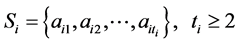 then by (2)
then by (2)
 . (3)
. (3)
Let
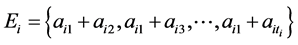 ,
, 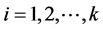 and
and
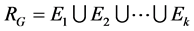 then the vectors of
then the vectors of  are independent. Hence by (3), the dimension of subspace
are independent. Hence by (3), the dimension of subspace 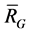 spanned by
spanned by 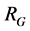 is
is
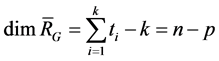 (4)
(4)
It is clear that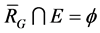 .
.
For the sufficiency, suppose that there exists an outerkernel subspace  with condition (1), and the dimension of
with condition (1), and the dimension of 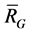 is
is![]() .
.
We divide the vertices of ![]() into some subsets according to the subspace
into some subsets according to the subspace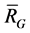 . If for two vertices
. If for two vertices 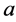 and
and  there have
there have
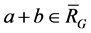 , (5)
, (5)
then we put 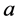 and
and 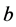 into a same subset. Like the notation of congruence we denote
into a same subset. Like the notation of congruence we denote
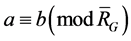 .
.
Obviously, if a vertex a appears in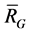 , then there has at least another vertex in the same subset with a. If a vertex does not appear in
, then there has at least another vertex in the same subset with a. If a vertex does not appear in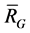 , then this vertex forms a subset by itself, i.e. the subset contains only one vertex.
, then this vertex forms a subset by itself, i.e. the subset contains only one vertex.
Lemma 5. The vertices from different subset are linear independence on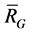 , i.e. if
, i.e. if  belong to different subsets respectively, then
belong to different subsets respectively, then
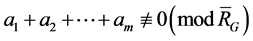 .
.
In fact, if , by Lemma 4, there exists a vertex
, by Lemma 4, there exists a vertex  such that
such that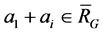 . That means
. That means 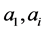 is in the same subset.
is in the same subset.
Now we go on with the proof of the sufficiency. Suppose that the 2-order vectors  form a basis of
form a basis of , and the vertices of the graph G are now divided into the disjoint subset
, and the vertices of the graph G are now divided into the disjoint subset  by the method above. Take
by the method above. Take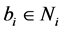 ,
,  , then any vertex a of G must be in some subset
, then any vertex a of G must be in some subset 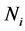 and by (5) we have
and by (5) we have
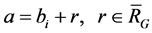 .
.
So any vertex of ![]() can be expressed by
can be expressed by 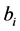 and an element of
and an element of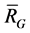 . Thus by Lemma 5,
. Thus by Lemma 5,

are the basis of linear space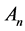 . Hence
. Hence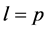 .
.
By the definition of 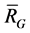 and (5) we know that the two vertices in the same subset
and (5) we know that the two vertices in the same subset 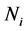 are non-adjacent. Thus, we can assign one color to the vertices of each subset
are non-adjacent. Thus, we can assign one color to the vertices of each subset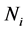 . So we just need p colors for G. The graph is
. So we just need p colors for G. The graph is ![]() -coloring.
-coloring.
Due to Theorem 1 and the expression (4), we have:
Theorem 2. For a graph G with n vertices, the sufficient and necessary condition for 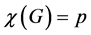 is that the rank of a maximal outer-kernel subspace
is that the rank of a maximal outer-kernel subspace  is
is![]() .
.
4. An Application to Plane Graphs
As an application of Theorem 1, we consider a result of the coloring to the plane graph.
A maximal plane graph is a graph G such that for any two non-adjacent vertices a and b of G, G added to the edge ab makes a non-planar graph. It is clear that all the faces of a maximal plane graph are triangles.
A maximal plane graph is 3-CR-edge coloring if we can color its edges by 3 colors such that the three edges of every its triangle face are coloring by different colors. Later we will see that the CR in the definition is borrowed from the Cauchy-Riemann condition in the complex function theory.
Theorem 3. If a maximal plane graph is 3-CR-edge coloring, then the graph is 4-vertex coloring.
The inverse of the Theorem 3 is true, too. That means if a maximal plane graph is 4-vertex coloring, then the graph is 3-CR-edge coloring.
Proof. We introduce the 2-demensional linear space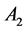 :
:
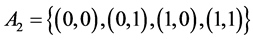 .
.
Let 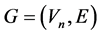 be 3-CR-edge coloring, and the all edges of G can map to the three elements
be 3-CR-edge coloring, and the all edges of G can map to the three elements
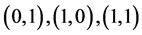 of
of 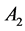 by their colors, respectively. That is the mapping f
by their colors, respectively. That is the mapping f
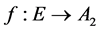
such that if  are the vertices of a face of G, then
are the vertices of a face of G, then
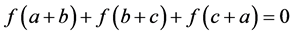 (6)
(6)
For a path of G with the end-point a, b and the sequence of the edges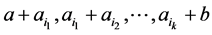 , we define
, we define
 . (7)
. (7)
By the condition of 3-CR-edge coloring, the extending mapping f by (7) is dependent only on the end-point a and b, and independent on their path.
Let  be the
be the  -dimensional linear subspace spanned by all the 2-order vectors of the space
-dimensional linear subspace spanned by all the 2-order vectors of the space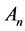 . Then f is the homomorphic mapping from subspace
. Then f is the homomorphic mapping from subspace 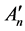 onto the space A2. The homomorphic kernel
onto the space A2. The homomorphic kernel 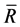 consists of such vector e of
consists of such vector e of 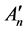 that satisfies
that satisfies
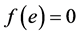 (8)
(8)
Suppose 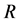 is the subset of 2-order vectors of
is the subset of 2-order vectors of 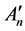 that satisfies (8) and
that satisfies (8) and 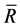 is spanned by R. Then by (8) we have
is spanned by R. Then by (8) we have
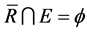 .
.
Denote the linear independent spanning elements of  by
by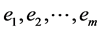 , that is just the basis of
, that is just the basis of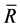 . And
. And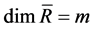 .
.
We take 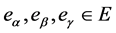 such that
such that
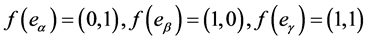 .
.
Then the linear subspace 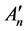 is spanning by
is spanning by
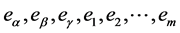 .
.
Hence![]() , and
, and . By Theorem 1, the graph G is 4-vertex coloring.
. By Theorem 1, the graph G is 4-vertex coloring.
[1] REFERENCES
[2] F. Harary, “Graph Theory,” Addison-Wesley, Boston, 1969.
[3] P. Erdös and A. Hajnal, “Chromatic Number of Finite and Infinite Graphs and Hypergraphs,” Discrete Mathematics, Vol. 53, 1985, pp. 281-285.
[4] N. Biggs, E. Lloyd and R. Wilson, “Graph Theory 1736- 1936,” Oxford University Press, Oxford, 1986.

