Open Journal of Discrete Mathematics
Vol.3 No.2(2013), Article ID:30170,8 pages DOI:10.4236/ojdm.2013.32015
Longest Hamiltonian in Nodd-Gon
Depto de Matemática, Universidad Nacional del Sur, Bahía Blanca, Argentina
Email: biniel@criba.edu.ar
Copyright © 2013 Blanca I. Niel. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received February 4, 2013; revised March 26, 2013; accepted April 15, 2013
Keywords: Hamiltonian path; Extremal problems; Euclidean geometric problem; Farthest Neighbor tours; Traveling Salesman Problem; Geometry of Odd Regular Polygons
ABSTRACT
We single out the polygonal paths of 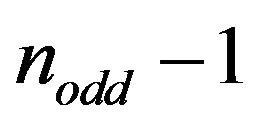 order that solve each of the
order that solve each of the  different longest non-cyclic Euclidean Hamiltonian path problems in
different longest non-cyclic Euclidean Hamiltonian path problems in  networks by an arithmetic algorithm. As by product, the procedure determines the winding index of cyclic Hamiltonian polygonals on the vertices of a regular polygon.
networks by an arithmetic algorithm. As by product, the procedure determines the winding index of cyclic Hamiltonian polygonals on the vertices of a regular polygon.
1. Introduction
Our aim implies to determine the overall lengths of every Longest Euclidean Hamiltonian Path Problems and the composition and the orderings of the directed segments that accomplish these longest Hamiltonian travels. The identification regardless of planar rotation and orientation is done with the proposed algorithm [1-3].
This paper apart from the Introduction, Conclusion and References contains §2 Algorithm and Hamiltonian Paths in Nodd-Gons and §3 Maximum Hamiltonian Path Problems in Nodd-Gons. §2 formulates specific Max. Hamiltonian Problems and postulates the algorithm for their resolutions. §3 devoted to the solution of the
 different Max. Traveling Salesman Path Problems in Nodd-Gons [4,5].
different Max. Traveling Salesman Path Problems in Nodd-Gons [4,5].
2. Algorithm and Hamiltonian Paths in Nodd-Gons
This work is focused in the resolution of the 
different Maximum Traveling Salesman Path Problems of order 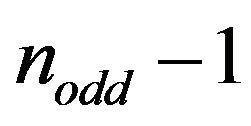 with inicial point at
with inicial point at 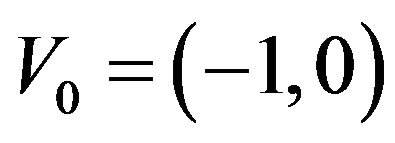 and final point at
and final point at 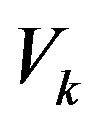 for
for 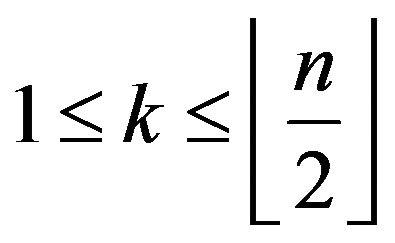 (see Figure 1) in the
(see Figure 1) in the
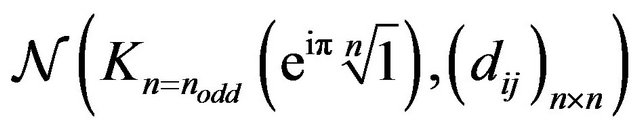 networks. These structures are built by the complete graph
networks. These structures are built by the complete graph 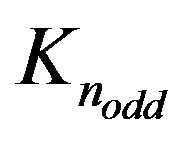 on the odd regular polygon vertices, i.e.
on the odd regular polygon vertices, i.e.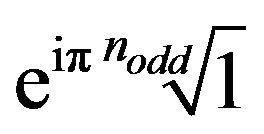 , and weighted with the Euclidean distances
, and weighted with the Euclidean distances 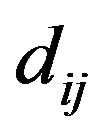 between nodes [6].
between nodes [6].
2.1. Intrinsic Geometry and Arithmetic
Let 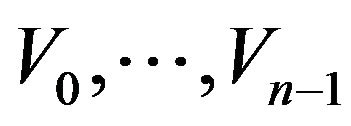 be the points of the
be the points of the 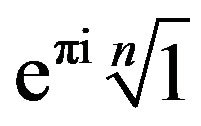 set and let them be clockwise enumerated by the integers modulo
set and let them be clockwise enumerated by the integers modulo ,
, 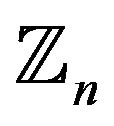 , from the vertex
, from the vertex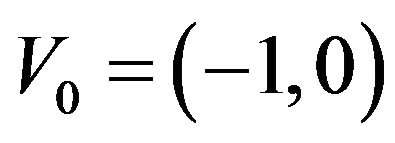 . For each
. For each 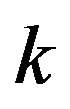 in
in
 and each
and each , let
, let  denote the segment that joins
denote the segment that joins 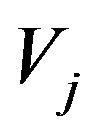 with
with , while
, while  denotes the one that joins
denotes the one that joins  to
to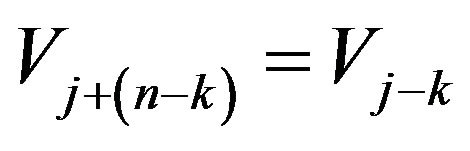 . From now onwards,
. From now onwards, 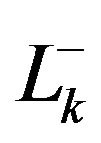 and
and 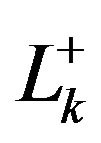 denote to
denote to 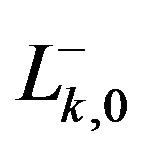 and
and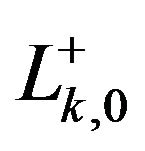 , respectively. Let
, respectively. Let  be the diameter, it joins the vertex
be the diameter, it joins the vertex  with its opposite
with its opposite , only if
, only if 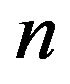 is even.
is even. 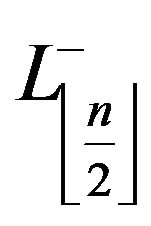 and
and  respectively designate the quasi-diameters if
respectively designate the quasi-diameters if  is odd (see Figure 1), [7].
is odd (see Figure 1), [7].
If  symbolizes a regular n-gon inscribed in the unitary circle and with vertices in
symbolizes a regular n-gon inscribed in the unitary circle and with vertices in ,
, 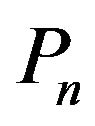 can be considered as the polygonal of sides
can be considered as the polygonal of sides 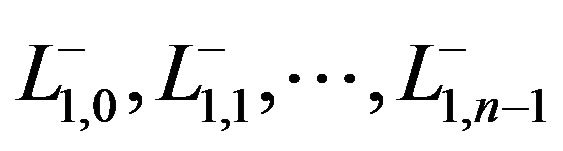 [8]. From the vectorial interpretation of the
[8]. From the vectorial interpretation of the 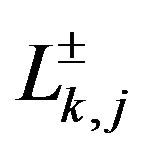 segments,
segments,  can be interpreted as the resultant of the polygonal of
can be interpreted as the resultant of the polygonal of  sides of
sides of , that joins clockwise
, that joins clockwise 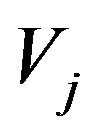 to
to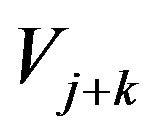 , while
, while 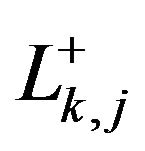 is the resultant of the polygonal of
is the resultant of the polygonal of  sides that joins clockwise
sides that joins clockwise 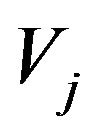 to
to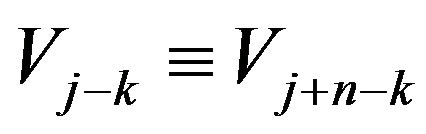 .
.

Figure 1. Lk segments in Nodd-Gons.
The segments 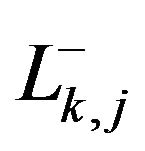 and
and 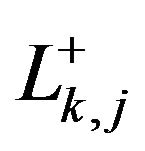 are the respective chords (or resultants) of the polygonals
are the respective chords (or resultants) of the polygonals 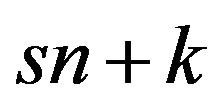 and
and 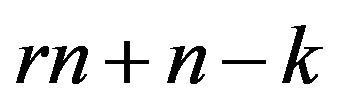 consecutive sides of
consecutive sides of , whichever are the integers
, whichever are the integers 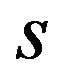 and
and . Therefore, it is natural to associate
. Therefore, it is natural to associate  with the integer
with the integer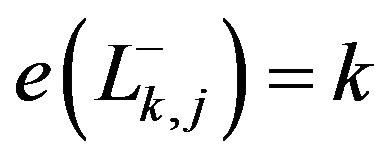 , and likewise
, and likewise 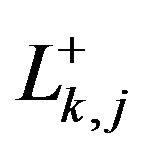 with the integer
with the integer .
.
Definition 2.1.1 For any integer ,
, 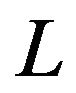 is a
is a  segment if for any
segment if for any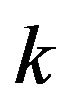 ,
, 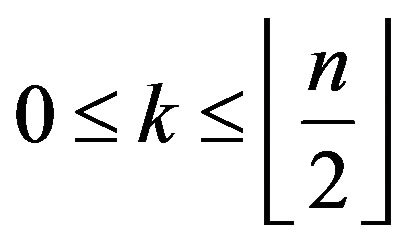 , and for any
, and for any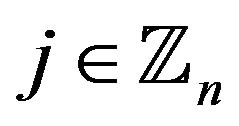 ,
,
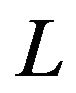 is equal to
is equal to 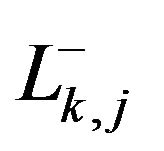 or
or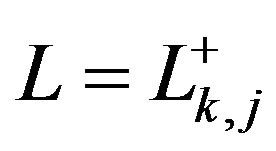 .
.
Definition 2.1.2 If  is an
is an 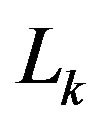 segment, the integer associated to
segment, the integer associated to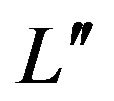 , noted as
, noted as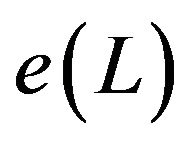 , is given by:
, is given by:
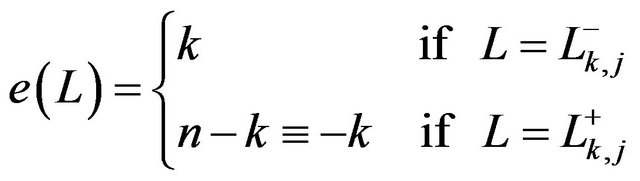
Definition 2.1.3 If 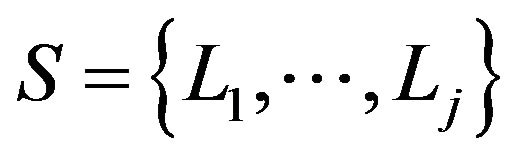 is a sequence of
is a sequence of 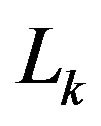 segments, the integer associated to the path evolved by
segments, the integer associated to the path evolved by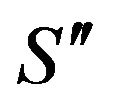 , is given by
, is given by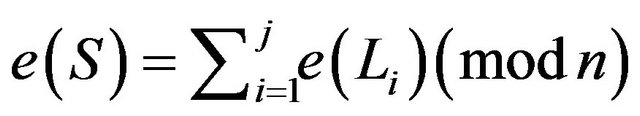 .
.
It should be taken into account the following facts:
• The consecutive collocation of two  segments from any vertex
segments from any vertex 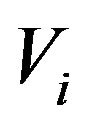 determines the vertex that corresponds to collocate, from
determines the vertex that corresponds to collocate, from 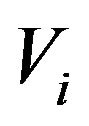 and in clockwise, as many sides of
and in clockwise, as many sides of  as correspond to the sum of the integers associated to each one of the two
as correspond to the sum of the integers associated to each one of the two 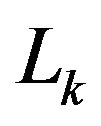 segments. In other words, the resultant of a polygonal built by two
segments. In other words, the resultant of a polygonal built by two  segments, is other
segments, is other 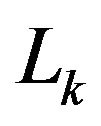 segment and its associated integer is the sum (modulo
segment and its associated integer is the sum (modulo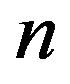 ) of the integers associated to the components of the polygonal.
) of the integers associated to the components of the polygonal.
• The 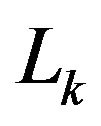 segment is
segment is 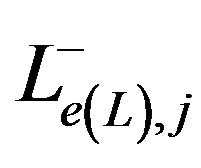 by considering any fixed value of
by considering any fixed value of , when
, when . Otherwise, if
. Otherwise, if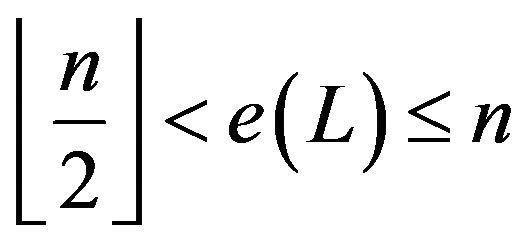 , is
, is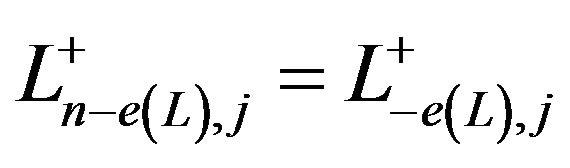 .
.
The concept of the associated integer  and its addition modulo
and its addition modulo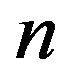 , deploy the following geometric correlate over the set of vertices
, deploy the following geometric correlate over the set of vertices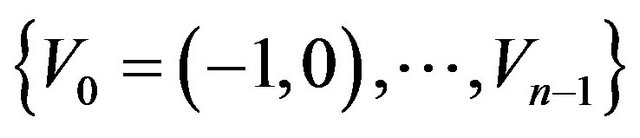 : For each
: For each ,
, 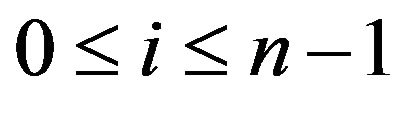 , the geometric place that corresponds to the vertex
, the geometric place that corresponds to the vertex  coincides with the place that corresponds to
coincides with the place that corresponds to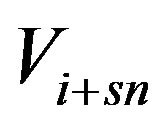 , for each integer
, for each integer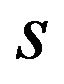 . Since the segments
. Since the segments 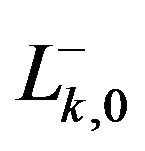 and
and  respectively connect the
respectively connect the
vertices 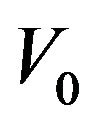 to
to  and
and 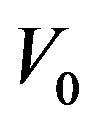 to
to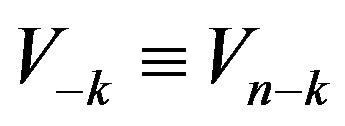 , it is clear that for any integer
, it is clear that for any integer 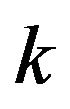 between 0 and
between 0 and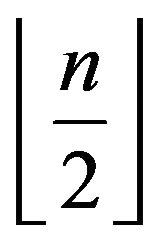 , the vertices
, the vertices
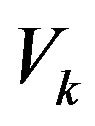 and
and 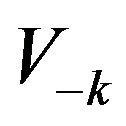 are symmetric with respect to the horizontal axis. Given a sequence of
are symmetric with respect to the horizontal axis. Given a sequence of 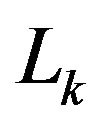 segments, henceforward the polygonal that they determine is in a oneto-one relationship with the sum of each one of these directed segments that belong to the sequence.
segments, henceforward the polygonal that they determine is in a oneto-one relationship with the sum of each one of these directed segments that belong to the sequence.
Since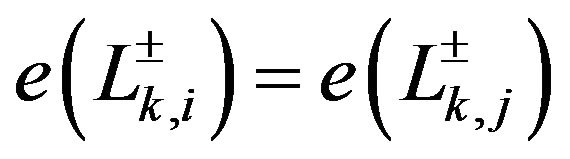 , whichever
, whichever 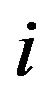 and
and  are, without loss of generality in the sequences of
are, without loss of generality in the sequences of 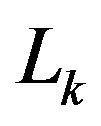 segments, the second subindices of these directed segments are rooted out.
segments, the second subindices of these directed segments are rooted out.
2.2. Resuming the Algorithm
Lemma 2.6 and Theorem 2.7 in [1] detail the proofs of the following algorithmic statements.
Theorem 2.2.1 The pathway determined by a sequence 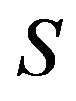 of
of 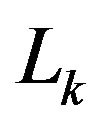 segments starts and ends at the same vertex
segments starts and ends at the same vertex  if and only if
if and only if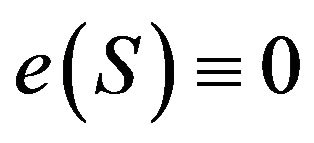 .
.
Theorem 2.2.2 A sequence 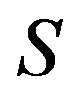 of
of 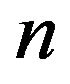
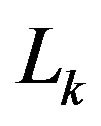 segments determines a Euclidean Hamiltonian cycle
segments determines a Euclidean Hamiltonian cycle  of order
of order 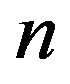 if and only if any proper subsequence of order
if and only if any proper subsequence of order 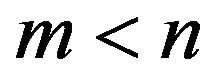 has associated integer neither
has associated integer neither 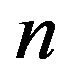 nor a multiple of
nor a multiple of 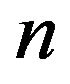 and
and .
.
Corollary 2.2.1 A sequence 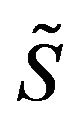 of
of  segments of order
segments of order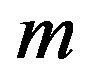 ,
, 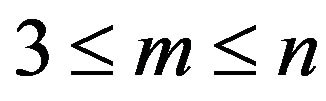 , building a Euclidean closed polygonal in
, building a Euclidean closed polygonal in  networks, passing once through certain or all
networks, passing once through certain or all 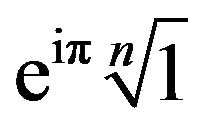 vertices, has
vertices, has .
.
Since, 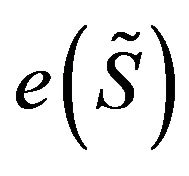 is a multiple of
is a multiple of  exists
exists  less than or equal to
less than or equal to  which counts the times that
which counts the times that 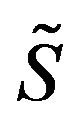 cw.
cw.
winds around the geometric centre of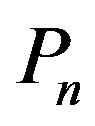 . We named this specific integer as the “winding index”.
. We named this specific integer as the “winding index”.
2.3. Applications of the Algorithm: Winding Index in Special Cyclic Paths in Nodd-Gons
Let 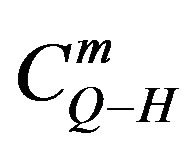 symbolize a cyclic polygonal in
symbolize a cyclic polygonal in
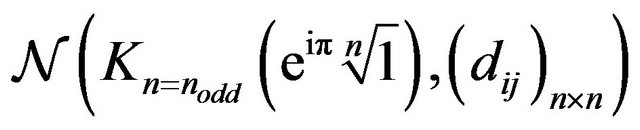 network, which does not repeat vertices, with the exception of the first and the last one, and which passes through certain
network, which does not repeat vertices, with the exception of the first and the last one, and which passes through certain  nodes,
nodes,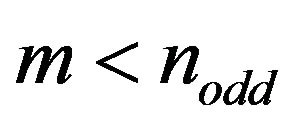 . Specially,
. Specially, 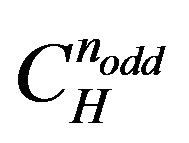 stands for Euclidean Hamiltonian cycles in
stands for Euclidean Hamiltonian cycles in 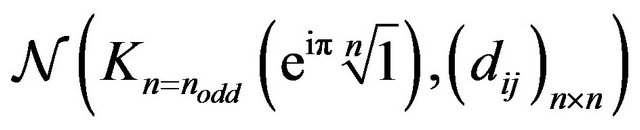 network.
network.
Exampe 2.1. Let 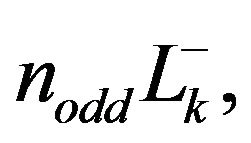
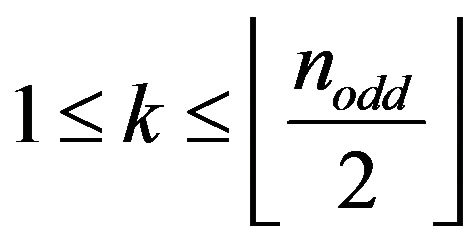 . If
. If  does not divide
does not divide  they are
they are 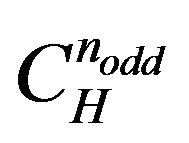 s of winding index
s of winding index 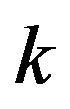
[9].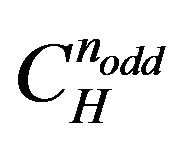 :
:  is the Max TSP [10].
is the Max TSP [10].
Exampe 2.2. Let
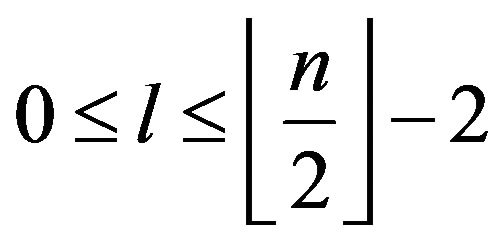
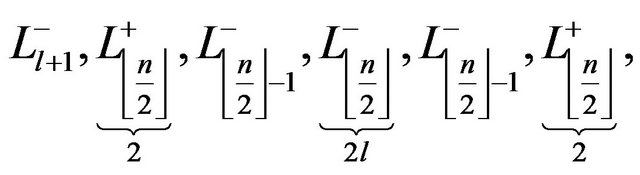 .
.
The angular cw. avance is proportional to:
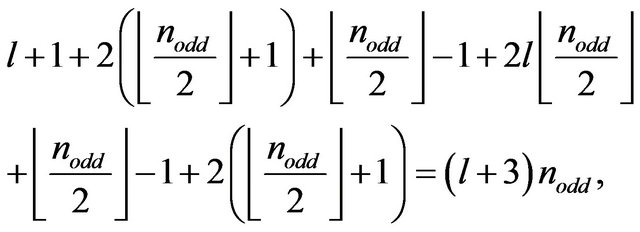
then 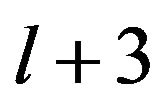 is the winding index. Algorithmic computations render that these cycles are
is the winding index. Algorithmic computations render that these cycles are 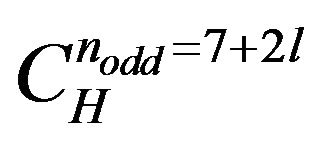 and
and 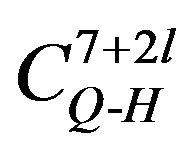 for networks built on
for networks built on . For
. For
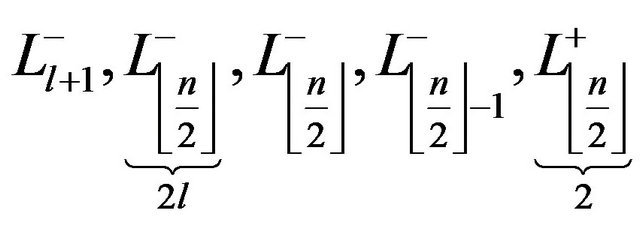 the algorithm prompts
the algorithm prompts 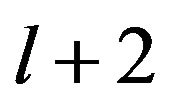
as winding index and singled out them as 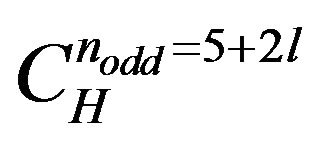 and
and
 if
if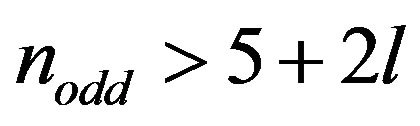 . In
. In ,
,
 , the algorithm characterizes these cycles as
, the algorithm characterizes these cycles as 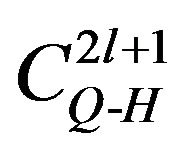 in
in  with winding index
with winding index .
.
Exampe 2.3. Table 1 deploys cycles living in

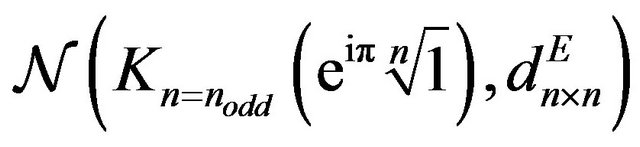 .
.
Exampe 2.4. Table 2 shows Euclidean Hamiltonian cycles in special  networks.
networks.
3. Maximum Hamiltonian Path Problems in Nodd-Gons
In 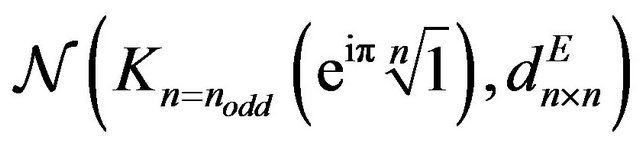 network for
network for we study the trajectories built by a single
we study the trajectories built by a single 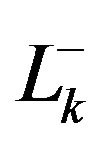 segmentTable 1.
segmentTable 1. 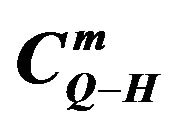 in
in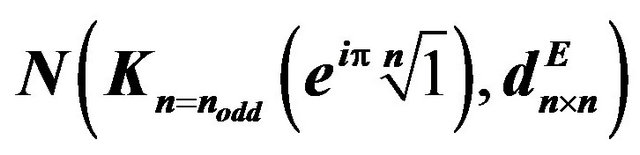 .
.

Table 2.  in
in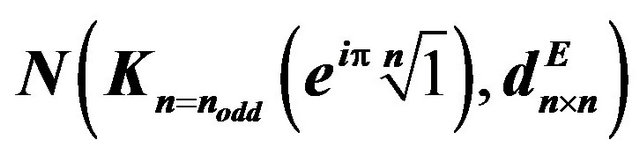 .
.

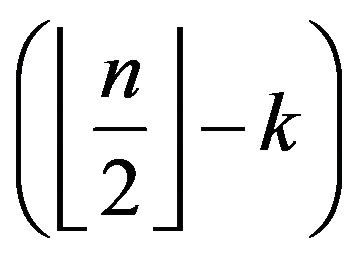 directed
directed 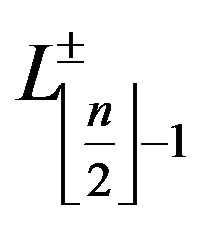 segments, and
segments, and 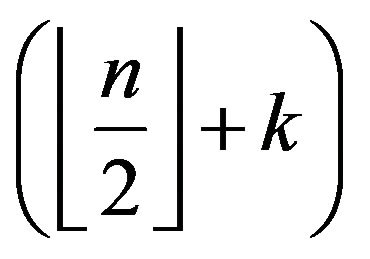
directed segments , that is (1).
, that is (1).
3.1. Lengths of Relevant Pathways
Our present concern is to study the Euclidean lengths and the composition of the directed segments that build the trajectories given by (1).
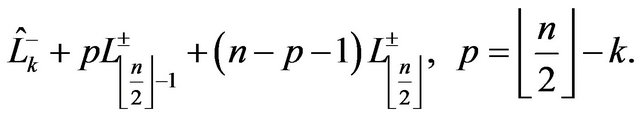 (1)
(1)
Since for  the lengths
the lengths 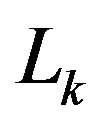 of the segments
of the segments
 ,
,  verify the following relationships:
verify the following relationships:
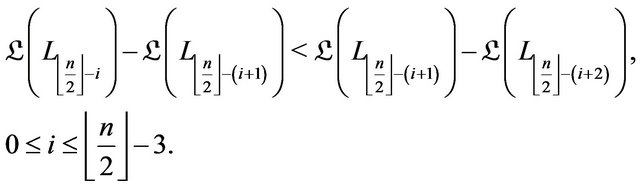
Therefore, the overall traveled Euclidean lengths of the pathways (1) are given by:
 (2)
(2)
Therein, precisely we focusing on the Euclidean Hamiltonian cycles,  s, which accomplish the lengths
s, which accomplish the lengths
(2) in  network.
network.
Next Theorem establishes the composition of the directed segments that give birth to the sequences with overall traveled lengths (2).
Theorem 3.1.1 The overall traveled lengths (2) in
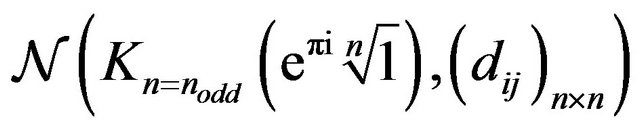 are accomplished for any sequence built by a single
are accomplished for any sequence built by a single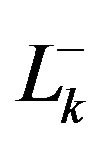 ,
, 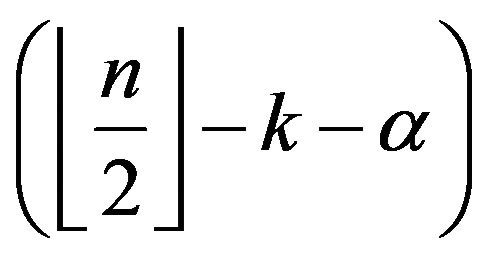
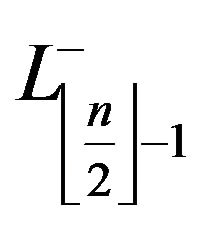 ,
, 
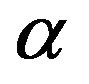 ,
, 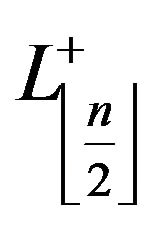
 and
and 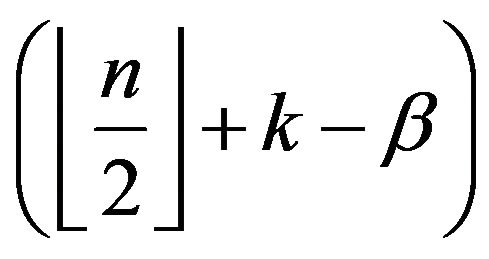
 directed segments if
directed segments if 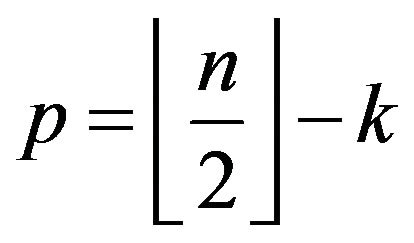 and
and  if the conditions in (3) are satisfied.
if the conditions in (3) are satisfied.
 (3)
(3)
Proof

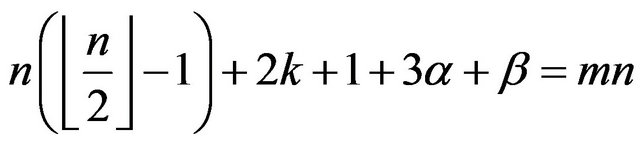
From the constraints  and
and
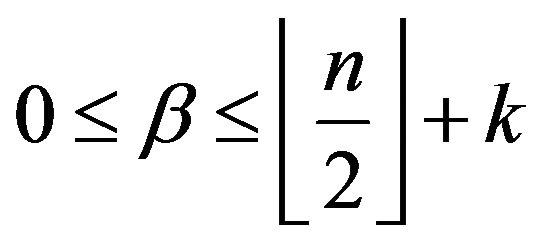 follows
follows
 should be
should be 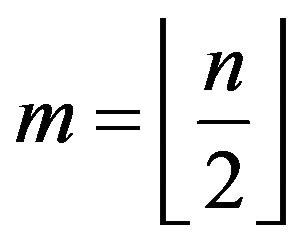 and hence
and hence
 . Therefore, the admissible couples
. Therefore, the admissible couples 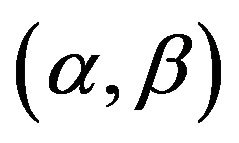 for the lengths (2) should verified (3). □
for the lengths (2) should verified (3). □
Backward recurrence over the traveled length in steepest descent steps from the max  to
to  constraint and the lack of Hamiltonian cycles for
constraint and the lack of Hamiltonian cycles for
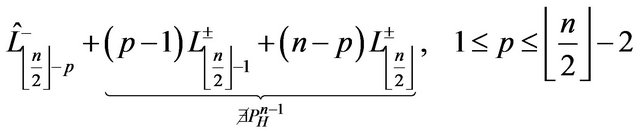
state that (4) is the Euclidean Hamiltonian Maximum Path length when  is rooted out.
is rooted out.
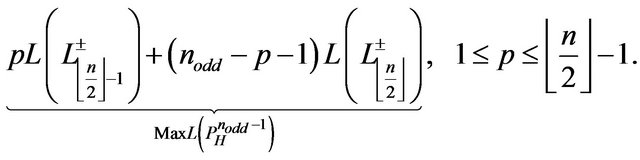 (4)
(4)
3.2. Specific Directed Segments for the Max. Traveling Salesman Path Problems in Nodd-Gons
We confirm in Theorem (3.3.1), Theorem (3.3.2) and Theorem (3.3.3) the existence of Euclidean Hamiltonian cycles that attain the overall Euclidean lengths given by the sequences (1) and the assignments (3).
1) For  if
if  and
and 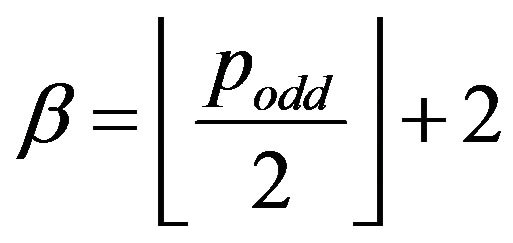 in
in
(3) exists 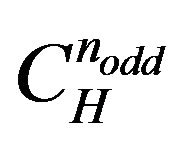 s with overall traveled length (2). See Theorem (3.3.1) at pg. 4.
s with overall traveled length (2). See Theorem (3.3.1) at pg. 4.
2) For 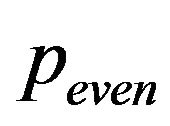
a) 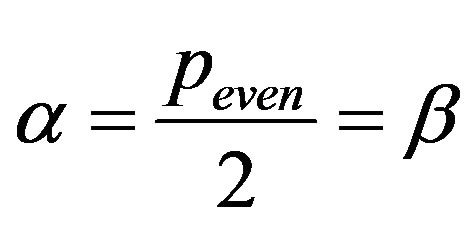 in (3) exists
in (3) exists  s with whole traveled length (2). See Theorem (3.3.2) at pg. 5b)
s with whole traveled length (2). See Theorem (3.3.2) at pg. 5b)  and
and 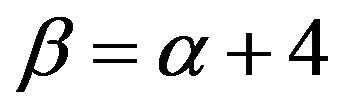 in (3) exists
in (3) exists 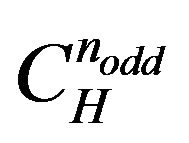 s with whole traveled length (2). See Theorem (3.3.3) at pg. 5.
s with whole traveled length (2). See Theorem (3.3.3) at pg. 5.
3.3. Orderings of the Directed Segments for the Max. Traveling Salesman Paths in Nodd-Gons
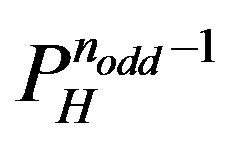 symbolizes any Euclidean Hamiltonian path that resolves the Max Traveling Salesman Path Problems with initial vertex
symbolizes any Euclidean Hamiltonian path that resolves the Max Traveling Salesman Path Problems with initial vertex 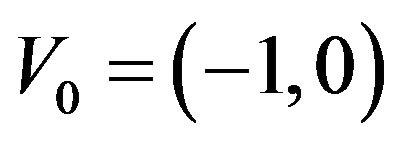 and final vertex
and final vertex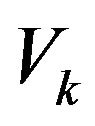 , that is whichever be the bridge,
, that is whichever be the bridge,  for
for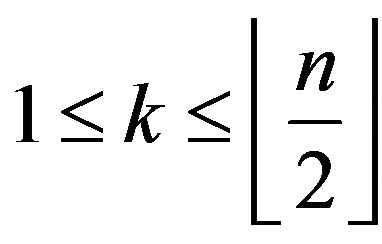 between the starting and ending points.
between the starting and ending points.
Observation 3.1 Proofs of Theorem 3.3.1, Theorem 3.3.2 and Theorem 3.3.3 result from direct application of Theorem 2.2.2 of the proposed algorithm.
Theorem 3.3.1 Let 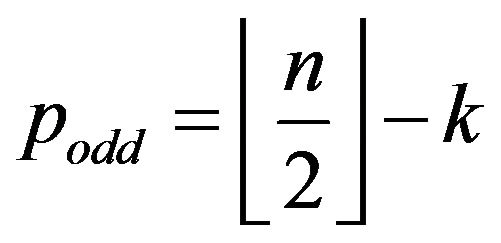 an odd integer for
an odd integer for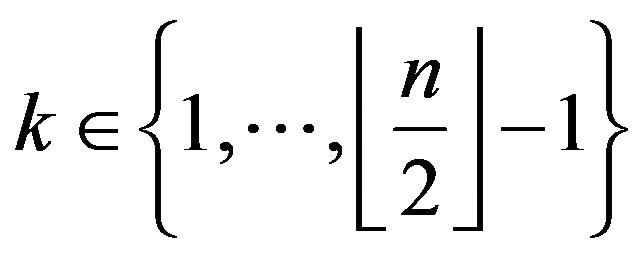 . The pathways (5) and (6) build
. The pathways (5) and (6) build
 s in
s in  networks if
networks if
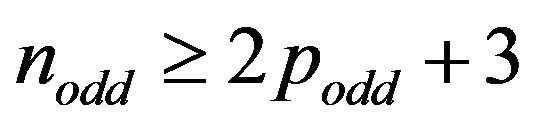 .
.
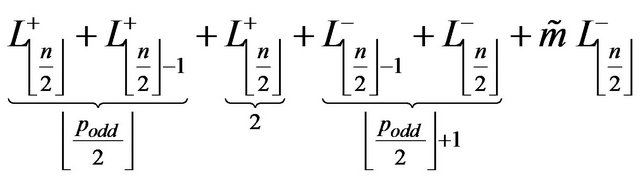 (5)
(5)

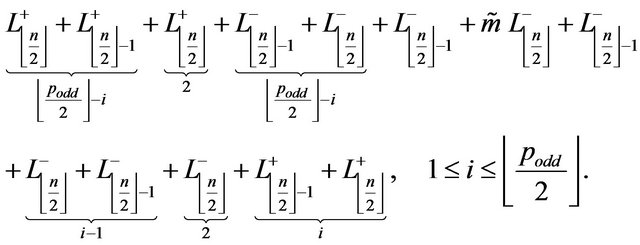 (6)
(6)
for . □
. □
Let  and
and  denote, respectively, the forward and backward readings of any sequence of
denote, respectively, the forward and backward readings of any sequence of  segments.
segments.
Corollary 3.3.1 In 
networks if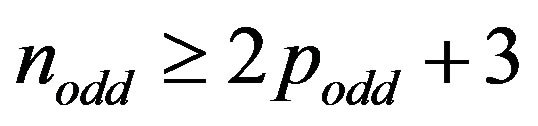 , forward and backward readings of the sequences (5) and (6) are
, forward and backward readings of the sequences (5) and (6) are .
.
Consequently,  and
and  of the sequence (5) and
of the sequence (5) and
(6) account for 2 plus to 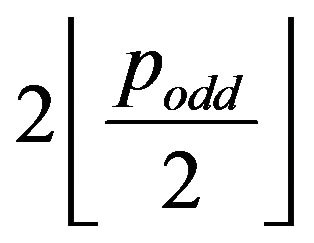 distinct sequencesrespectively. Furthermore,
distinct sequencesrespectively. Furthermore,  and
and  of the pathway (5) and paths (6) build
of the pathway (5) and paths (6) build 
 s if the directed segment
s if the directed segment  is initially appended to these sequences. □
is initially appended to these sequences. □
Theorem 3.3.2 Let 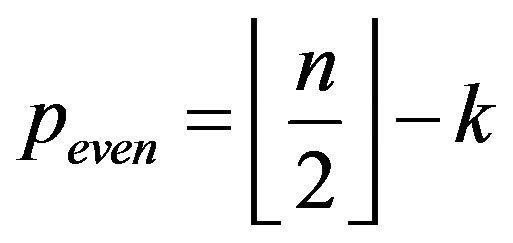 an even integer for
an even integer for . The pathways (7) and (8) build
. The pathways (7) and (8) build 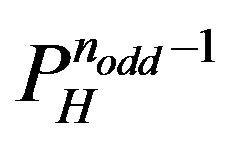 s in
s in 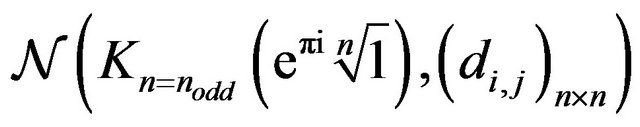 networks if
networks if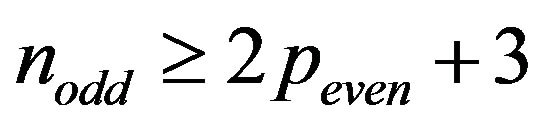 , with
, with 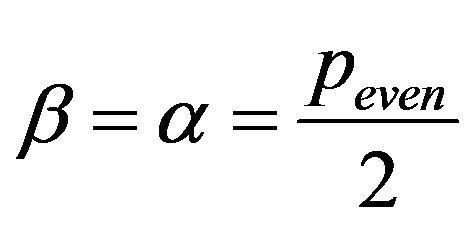 is the number of
is the number of 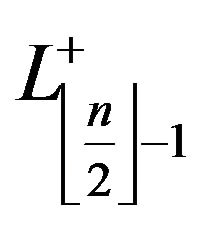 and
and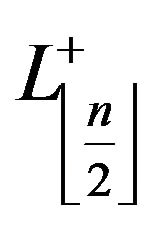 , respectively.
, respectively.
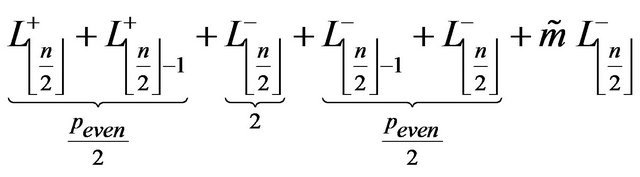 (7)
(7)
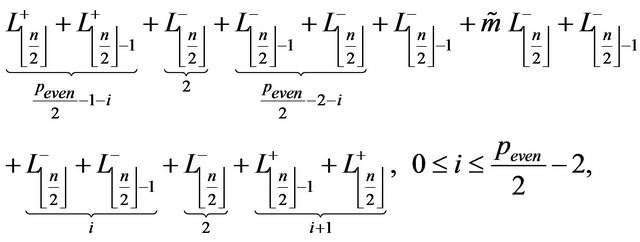 (8)
(8)
for 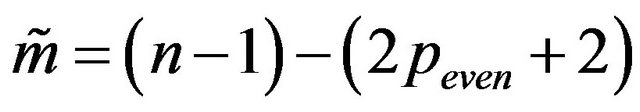 □
□
Corollary 3.3.2 In 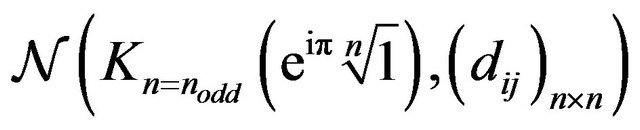 networks if
networks if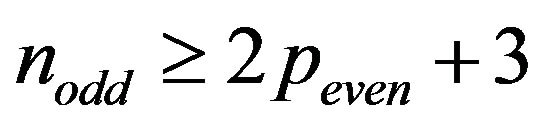 , forward and backward readings of the sequences (7) and (8) are
, forward and backward readings of the sequences (7) and (8) are . Particularly, the enumeration of the distinct
. Particularly, the enumeration of the distinct  s given birth from the forward and backward readings of the sequences (8) depend on the
s given birth from the forward and backward readings of the sequences (8) depend on the  evenness. Specifically1) If
evenness. Specifically1) If 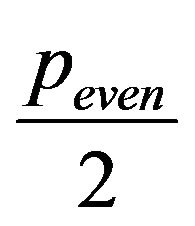 is odd, since
is odd, since 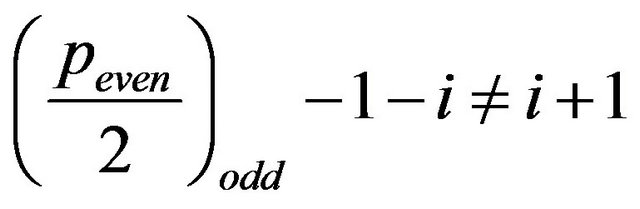
every sequence in (8) is not a palindrome [1]. Moreoverthe 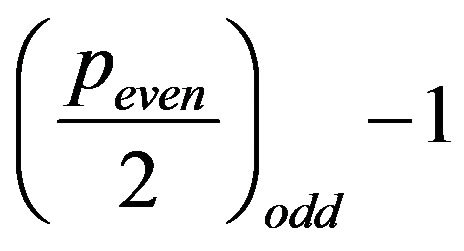 sequences defined in (8) are in couples
sequences defined in (8) are in couples  and
and  Specifically, the
Specifically, the  path
path
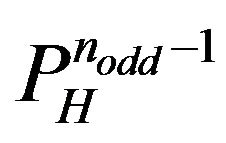 determined by
determined by  coincides to
coincides to  path
path
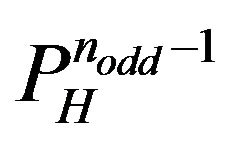 determined by
determined by ,
, 
 path coincides with
path coincides with 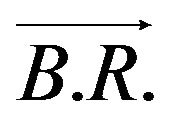 of the sequence defined by
of the sequence defined by
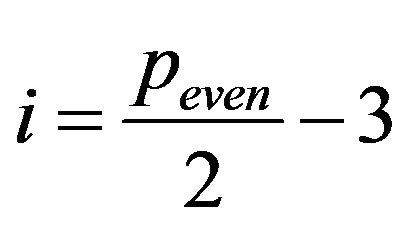 and so on. That is the
and so on. That is the 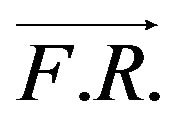 paths defined by (8) with
paths defined by (8) with 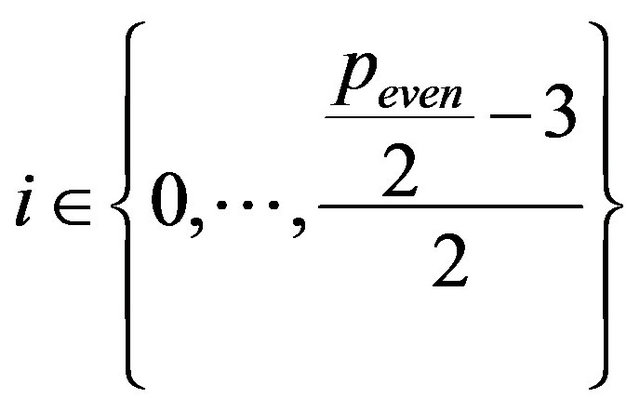 coincide with the
coincide with the
 paths determined by (8) with
paths determined by (8) with
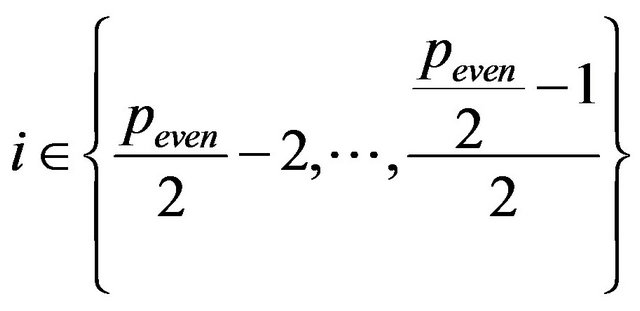 .
.
Therefore, exists 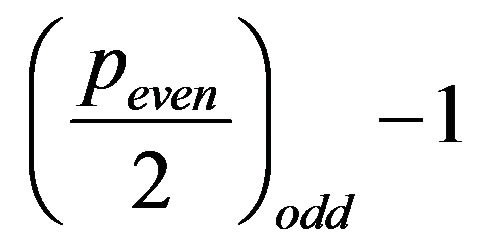 distinct
distinct 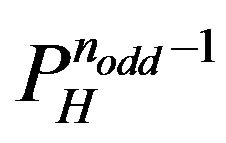 s which correspond with each one of the
s which correspond with each one of the  determined by (8). Since
determined by (8). Since 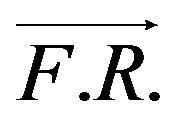 of (7) is different to its
of (7) is different to its , both
, both
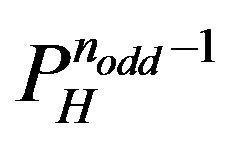 s should be added to the final enumeration. In conclusion, the distinct
s should be added to the final enumeration. In conclusion, the distinct 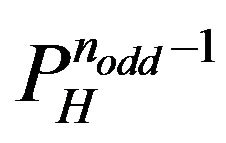 s are
s are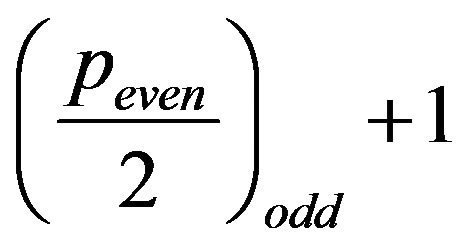 .
.
2) If 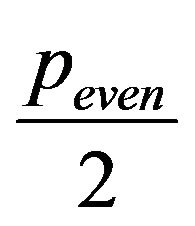 is even, since
is even, since , then
, then 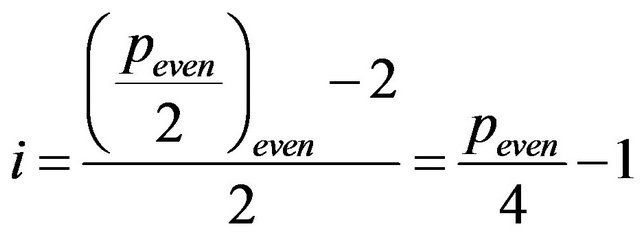 this index in (8) builds a
this index in (8) builds a  which is a palindrome [1]. In addition,
which is a palindrome [1]. In addition, 
paths defined by (8) with 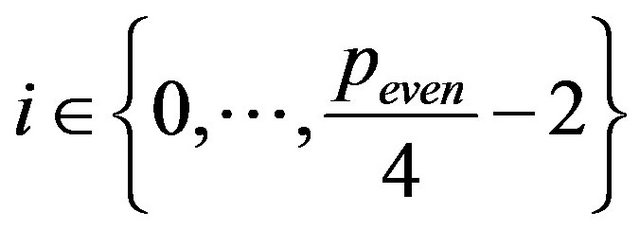 coincide with the
coincide with the  paths determined by (8) with
paths determined by (8) with
 . Therefore, exists
. Therefore, exists
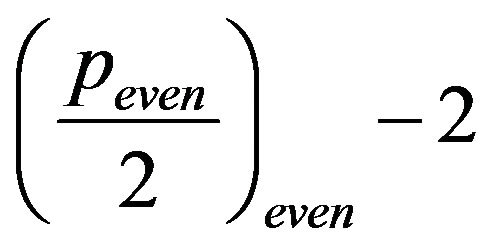 distinct
distinct  s which correspond with each one of
s which correspond with each one of  paths determined by (8). Since
paths determined by (8). Since 
of (7) is different to its , both
, both  s should be added to the final enumeration. In conclusion, the distinct
s should be added to the final enumeration. In conclusion, the distinct
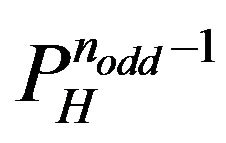 s are
s are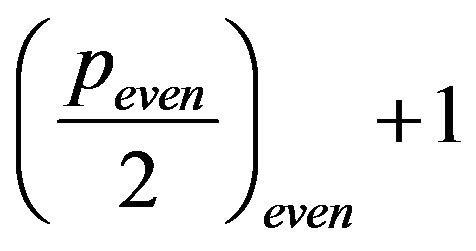 . □
. □
Theorem 3.3.3 Let 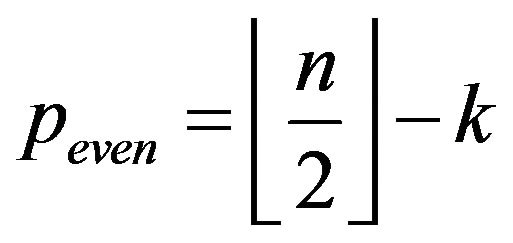 an even integer for
an even integer for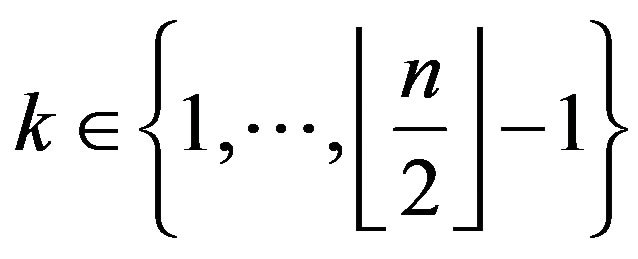 . The pathways (9) build
. The pathways (9) build  s in
s in 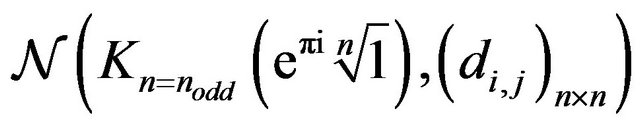 networks if
networks if
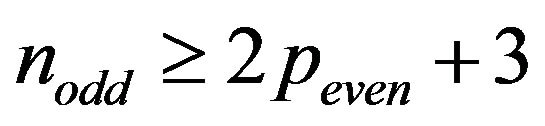 , meanwhile
, meanwhile  is the number of
is the number of 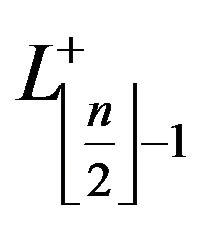 and
and  the amount of
the amount of .
.
 (9)
(9)
for . □
. □
Corollary 3.3.3 In  networks if
networks if , forward and backward readings of the sequences (9) are
, forward and backward readings of the sequences (9) are 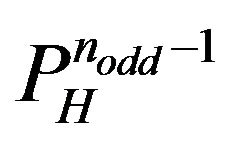 s. Particularly, the enumeration of the distinct
s. Particularly, the enumeration of the distinct 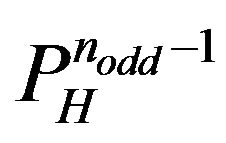 s given birth from the forward and backward readings of the sequences (9)
s given birth from the forward and backward readings of the sequences (9)
depend on the 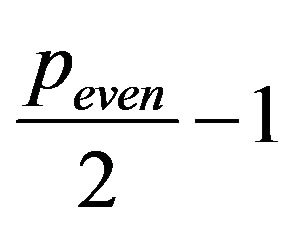 evenness. Specifically,
evenness. Specifically,
1) If 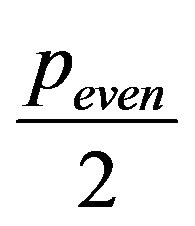 is odd, i.e.
is odd, i.e. 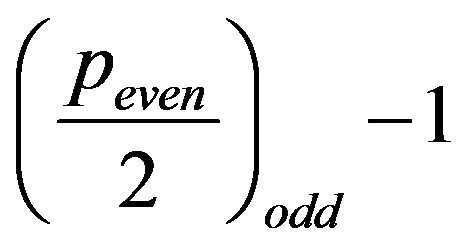 is even, then
is even, then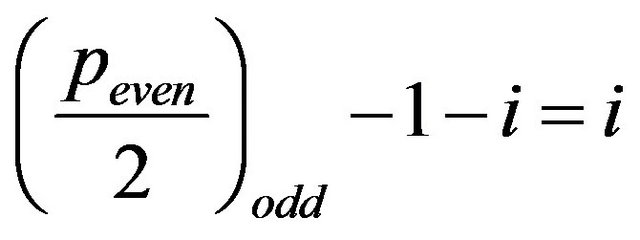 , therefore the sequence in (9) build by this index
, therefore the sequence in (9) build by this index 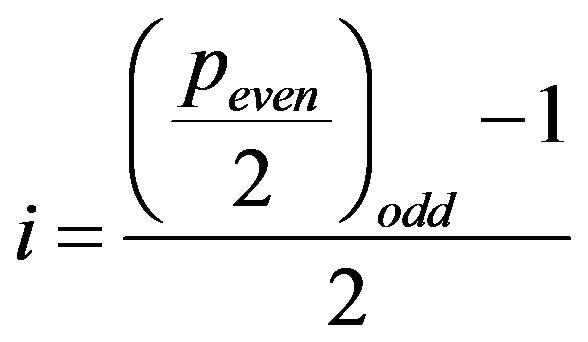 is a palindrome [1]. Moreover,
is a palindrome [1]. Moreover,  sequences defined in (9) are in couples
sequences defined in (9) are in couples  and
and  with the exception of that given birth by the index
with the exception of that given birth by the index 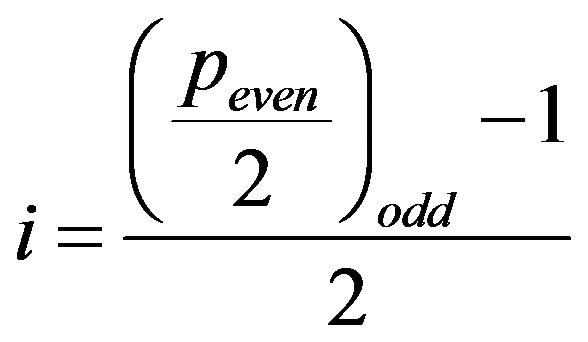 which its
which its
 and
and  is exactly the same pathway at all.
is exactly the same pathway at all.
Specifically, the  path
path 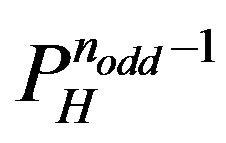 determined by
determined by
 coincides to
coincides to  path
path  determined by
determined by
 ,
, 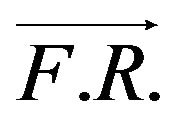
 path coincides with
path coincides with
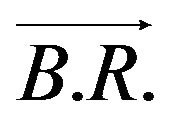 of the sequence defined by
of the sequence defined by 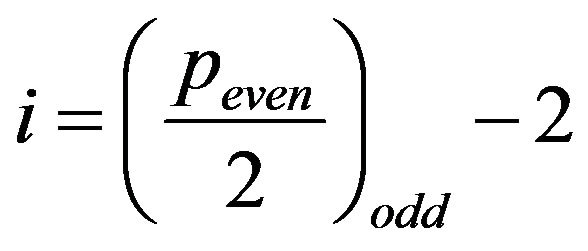 and so on, until the index
and so on, until the index  at which
at which 
and 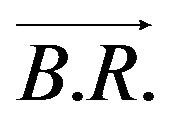 beget only one path. That is the
beget only one path. That is the  paths defined by (9) with the downgraded indexes
paths defined by (9) with the downgraded indexes
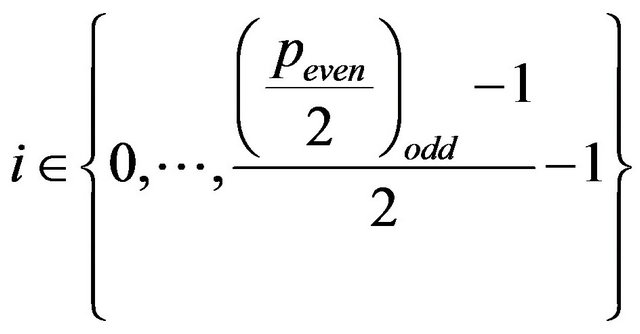 coincide with the
coincide with the 
paths determined by (9) with
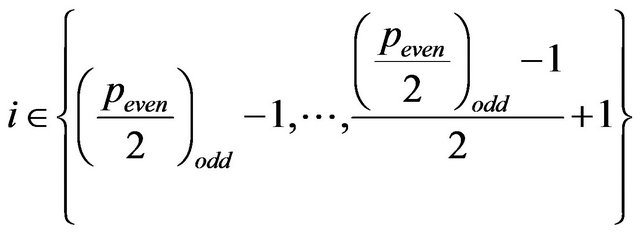 .
.
In conclusion, exists 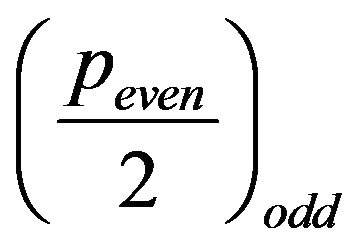 distinct
distinct 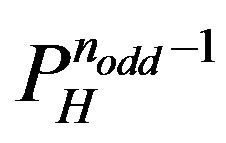 s which correspond with each one of the
s which correspond with each one of the  path determined by (9).
path determined by (9).
2) If 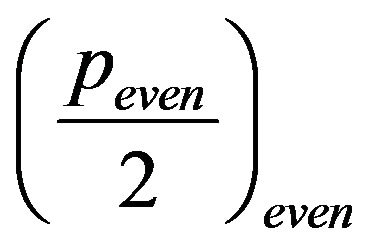 is even, i.e.
is even, i.e. 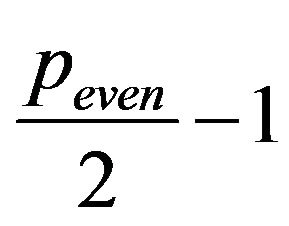 is odd, since
is odd, since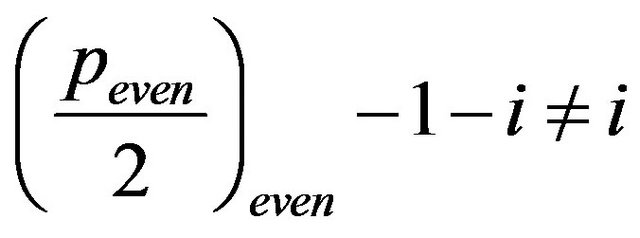 , then sequences (9) build
, then sequences (9) build  s none of them are palindrome [1]. In addition,
s none of them are palindrome [1]. In addition, 
paths of the indexes 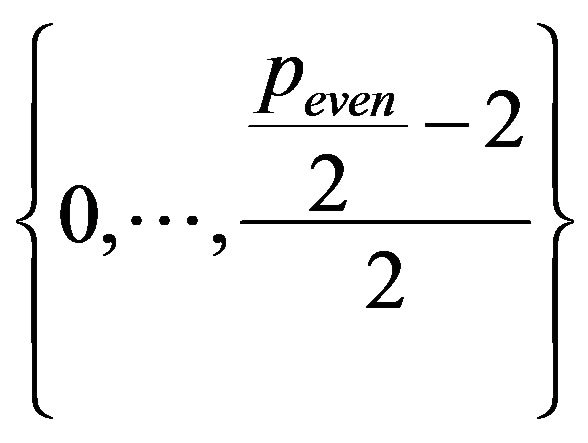 coincides with
coincides with
 paths of the downgraded indexes
paths of the downgraded indexes
 , respectively. In conclusion, exists
, respectively. In conclusion, exists 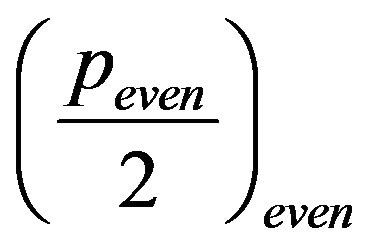 distinct
distinct 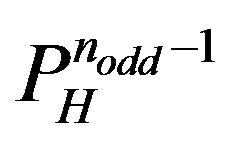 s vis-à-vis with each one of the
s vis-à-vis with each one of the  path determined by (9). □
path determined by (9). □
Observation 3.2 Corollary 3.3.1, Corollary 3.3.2 and Corollary 3.3.3 result from Theorem 3.3.1, Theorem 3.3.2 and Theorem 3.3.3, respectively.
In conclusion, the  s which resolve the Max.
s which resolve the Max.
Euclidean Hamiltonian Path Problems with the 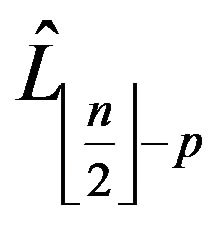
as the bridge between the endings of the Hamiltonian paths are evolved by the sequences (5) and (6) if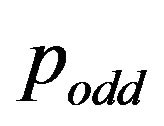 . Otherwise by the orderings (7)-(9). Moreover, with the exception of the palindromes their backward readings also resolve these specific Max. Traveling Salesman Problems.
. Otherwise by the orderings (7)-(9). Moreover, with the exception of the palindromes their backward readings also resolve these specific Max. Traveling Salesman Problems.
3.4. Bicoupled Nodd-Gons TSP Conjeture
We choose the geometric paths that start up at  of the quasi-spherical mirror of unitary radius, touch
of the quasi-spherical mirror of unitary radius, touch 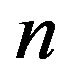 times-including the last touchinganywhere on the hollowed mirror, and end up at
times-including the last touchinganywhere on the hollowed mirror, and end up at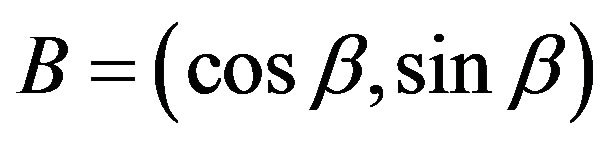 , with
, with 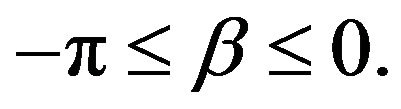 In this geometry each
In this geometry each  array of angles
array of angles , see Figure 2, denoted
, see Figure 2, denoted , determines a path with
, determines a path with  verticesincluding the initial and arrival pointsand
verticesincluding the initial and arrival pointsand  linear branches, [8,11,12]. This path may have two or more coincident vertices and linear branches shrunk to a point. For each
linear branches, [8,11,12]. This path may have two or more coincident vertices and linear branches shrunk to a point. For each 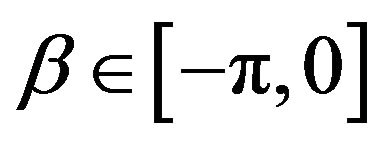 the
the 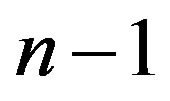 angles
angles 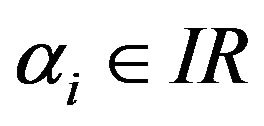 are selected (see Figure 2) as independent variables of the overall traveled length function of the paths
are selected (see Figure 2) as independent variables of the overall traveled length function of the paths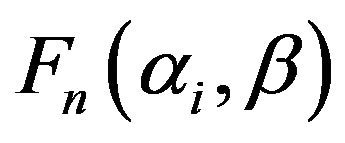 .
.
The length of the geometric path determined by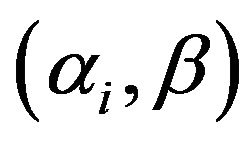 , is given by (10)
, is given by (10)
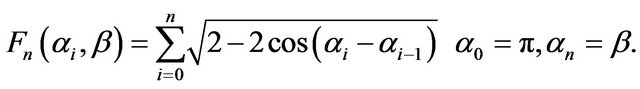 (10)
(10)
When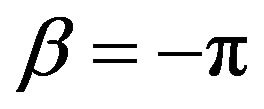 ,
,  , for any polygonal cyclic trajectory, there is an
, for any polygonal cyclic trajectory, there is an  -array
-array  which characterizes them. In particular, amongst these pathways are those that have as vertices the
which characterizes them. In particular, amongst these pathways are those that have as vertices the  points, with
points, with 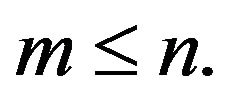 See [10] Theorem 2.1.1. and Appendix A, from page 78 to 80 [8]. Let
See [10] Theorem 2.1.1. and Appendix A, from page 78 to 80 [8]. Let
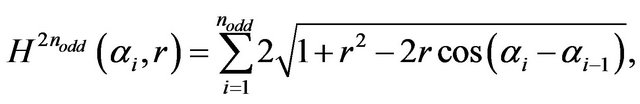 (11)
(11)
be a generalized length of (10), where 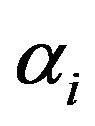 are the analogous angular parameters with the restraints
are the analogous angular parameters with the restraints 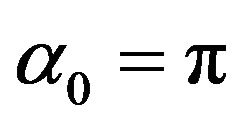 and
and , and
, and  in
in 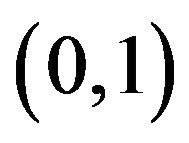 is the structural parameter for the locations of the coupled vertices of the inner
is the structural parameter for the locations of the coupled vertices of the inner 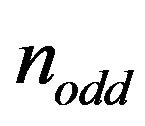 -polygon,
-polygon,
 networks [3].
networks [3].
Herein, see Figure 3, we pose the following conjeture: Are Max. TSPs in bilayer
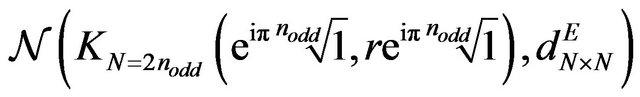 networks baited for the regular shapes of the Max. TSP in
networks baited for the regular shapes of the Max. TSP in 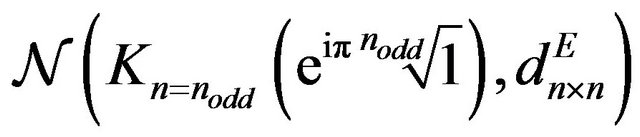 networks?
networks?
4. Conclusion
This paper is an offspring of a series of previous works about Hamiltonian maximum overall traveled lengths in
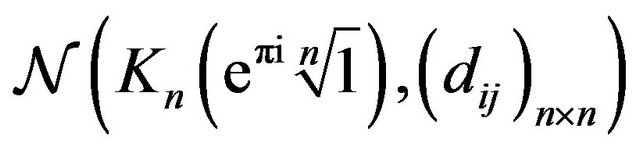 networks. Herein are singled out all the Euclidean Hamiltonian pathways that resolve
networks. Herein are singled out all the Euclidean Hamiltonian pathways that resolve

Figure 2. Measure of αi angular parameter.
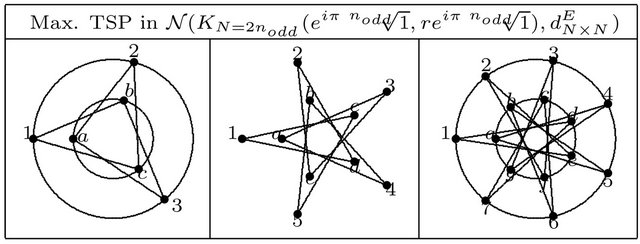
Figure 3. Max TSP in coupled Nodd-Gons.
the 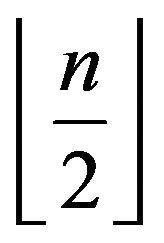 different maximum traveled Hamiltonian paths of order
different maximum traveled Hamiltonian paths of order  in
in 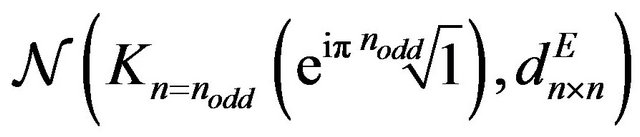
networks. As a by-product the proposed algorithm allow us to determine the winding index of specific cyclic polygonals. The approach is a step forward on the intrinsic geometry and inherent arithmetic of the vertex locus of the Nodd-Gons.
REFERENCES
- B. I. Niel, “Every Longest Hamiltonian Path in Even N-Gons,” Discrete Mathematics, Algorithms and Applications, Vol. 4, No. 4, 2012, p. 16. doi:10.1142/S1793830912500577
- B. I. Niel, “Viajes Sobre Nodd-Gons,” EAE, 2012.
- B. I. Niel, W. A. Reartes and N. B. Brignole, “Every Longest Hamiltonian Path in Odd Nodd-Gons,” SIAM Conference on Discrete Mathematics, Austin, 14-17 June 2010, p. 42.
- D. Applegate, R. Bixby, V. Chavatal and W. Cook, “Traveling Salesman Problem: A Computational Study,” Princeton University Press, Princeton, 2006.
- A. Barvinok, E. K. Gimadi and A. I. Serdyukov, “The Maximum Traveling Salesman Problem,” In: G. Gutin and A. P. Punnen, Eds., The Traveling Salesman Problem and Its Variations, Kluwer Academic Publishers. Dordrecht, 2002.
- F. Buckly and F. Harary, “Distance in Graphs,” Addison-Wesley Publishing Co., Boston, 1990.
- S. P. Fekete, H. Meijer, A. Rohe and W. Tietze, “Solving a ‘Hard’ Problem to Approximate an ‘Easy’ One: Heuristics for Maximum Matchings and Maximum Traveling Salesman Problems,” Journal of Experimental Algorithms, Vol. 7, 2002, 11 Pages.
- A. Kirillov, “On Regular Polygons, Euler’s Function, and Fermat Numbers,” In: S. Tabachnikov, Ed., Kvant Selecta: Algebra and Analysis, Amer Mathematical Society, Providence, 1999, pp. 87-98.
- H. S. M. Coxeter, “Introduction to Geometry,” John Wiley & Sons, Inc., Hoboken, 1963.
- B. I. Niel, “Geometry of the Euclidean Hamiltonian Suboptimal and Optimal Paths in the
 ’s Networks,” Proceedings of the VIII Dr. Antonio A. R. Monteiro, Congress of Mathematics, 26-28 May 2005, Bahía Blanca, pp. 67-84. http://inmabb.criba.edu.ar/cm/actas/pdf
’s Networks,” Proceedings of the VIII Dr. Antonio A. R. Monteiro, Congress of Mathematics, 26-28 May 2005, Bahía Blanca, pp. 67-84. http://inmabb.criba.edu.ar/cm/actas/pdf - W. R. Hamilton, “On a General Method of Expressing the Paths of Light, and of the Planets, by the Coefficients of a Characteristic Function,” Vol. I, Dublin University Review and Quarterly Magazine, Dublin, 1833, pp. 795-826.
- B. I. Niel, “Hamilton’s Real Find on Geometric Optics in a Hamiltonian Play,” Proceedings of Modelling and Simulation, MS’2004, Lyon, 5-7 July 2004, pp. 9.9-9.13

