Open Journal of Discrete Mathematics
Vol.3 No.1(2013), Article ID:27359,6 pages DOI:10.4236/ojdm.2013.31001
Chromatic Number of Graphs with Special Distance Sets-V
Department of Mathematics, Velammal Engineering College, Chennai, India
Email: prof.yegna@gmail.com, mathparthi@gmail.com
Received August 22, 2012; revised September 22, 2012; accepted September 30, 2012
Keywords: Primes; Chromatic Number; Distance Graphs
ABSTRACT
An integer distance graph is a graph  with the set of integers as vertex set and an edge joining two vertices u and
with the set of integers as vertex set and an edge joining two vertices u and 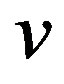 if and only if
if and only if 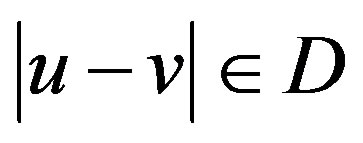 where D is a subset of the positive integers. It is known that
where D is a subset of the positive integers. It is known that  where P is a set of Prime numbers. So we can allocate the subsets D of P to four classes, accordingly as
where P is a set of Prime numbers. So we can allocate the subsets D of P to four classes, accordingly as 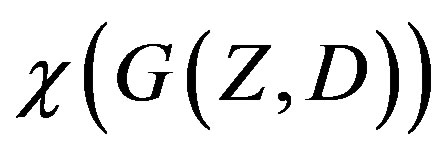 is 1 or 2 or 3 or 4. In this paper we have considered the open problem of characterizing class three and class four sets when the distance set D is not only a subset of primes P but also a special class of primes like Additive primes, Deletable primes, Wedderburn-Etherington Number primes, Euclid-Mullin sequence primes, Motzkin primes, Catalan primes, Schröder primes, Non-generous primes, Pell primes, Primeval primes, Primes of Binary Quadratic Form, Smarandache-Wellin primes, and Highly Cototient number primes. We also have indicated the membership of a number of special classes of prime numbers in class 2 category.
is 1 or 2 or 3 or 4. In this paper we have considered the open problem of characterizing class three and class four sets when the distance set D is not only a subset of primes P but also a special class of primes like Additive primes, Deletable primes, Wedderburn-Etherington Number primes, Euclid-Mullin sequence primes, Motzkin primes, Catalan primes, Schröder primes, Non-generous primes, Pell primes, Primeval primes, Primes of Binary Quadratic Form, Smarandache-Wellin primes, and Highly Cototient number primes. We also have indicated the membership of a number of special classes of prime numbers in class 2 category.
1. Introduction
The graphs considered in this paper are simple and undirected. A  -coloring of a graph
-coloring of a graph 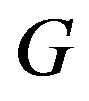 is an assignment of
is an assignment of 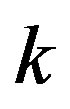 different colors to the vertices of
different colors to the vertices of 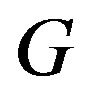 such that adjacent vertices receive different colors. The minimum cardinality
such that adjacent vertices receive different colors. The minimum cardinality 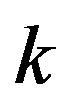 for which
for which  has a
has a 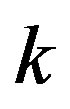 -coloring is called the chromatic number of
-coloring is called the chromatic number of 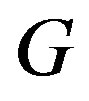 and is denoted by
and is denoted by 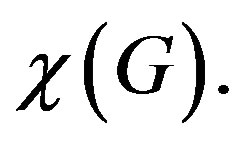 Let
Let 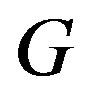 and
and  be graphs with
be graphs with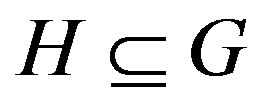 , then it is easy to see that
, then it is easy to see that  and so
and so 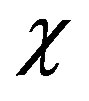 is a monotone function.
is a monotone function.
We begin with the plane coloring problem. What is the least number of colors needed to color all the points of the Euclidean plane such that no two points of distance one have the same color? The corresponding problem for the real line is easy. 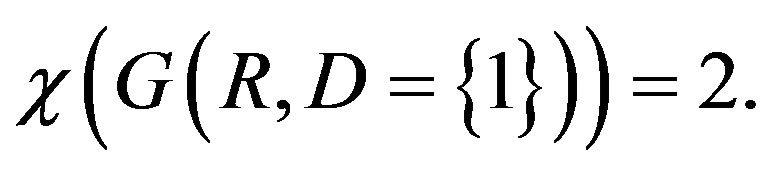 To see this, partition the vertex set of
To see this, partition the vertex set of  into two non empty disjoint sets such that their union is
into two non empty disjoint sets such that their union is .
.
That is, 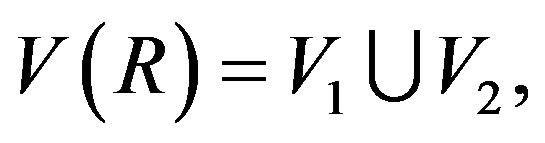 where
where 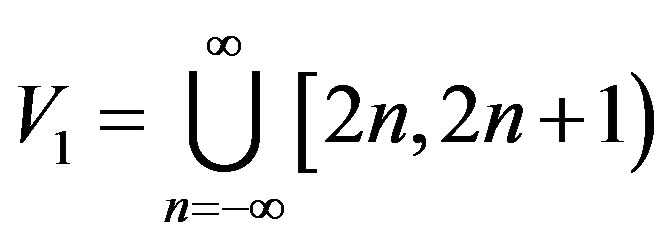
and 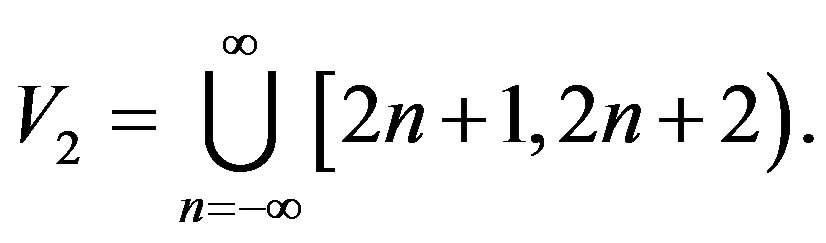 Now color all the vertices
Now color all the vertices

Figure 1. A sample Distance graph  with
with .
.
of 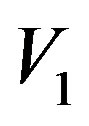 with color 1 and the vertices of
with color 1 and the vertices of  with color 2.
with color 2.
As  are independent and
are independent and 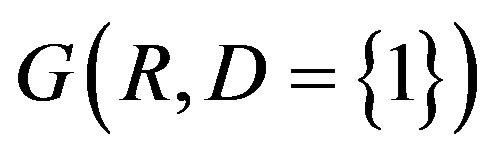 is bipartite the result follows. Clearly
is bipartite the result follows. Clearly  is an infinite graph. The problem of finding the chromatic number of
is an infinite graph. The problem of finding the chromatic number of 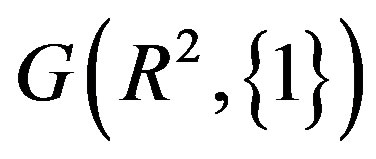 is enormously difficult. Paul Erdos has mentioned this problem as one of his favorite problems. Although he could not solve this problem he has made a significant progress towards the solution of this problem with a vital result given as follows: First let us state the famous Rado’s Lemma [1].
is enormously difficult. Paul Erdos has mentioned this problem as one of his favorite problems. Although he could not solve this problem he has made a significant progress towards the solution of this problem with a vital result given as follows: First let us state the famous Rado’s Lemma [1].
Lemma 1.1 Let  and
and 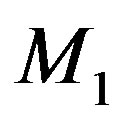 be arbitrary sets. Assume that to any
be arbitrary sets. Assume that to any 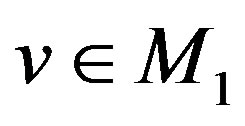 there corresponds a finite subset
there corresponds a finite subset  of
of . Assume that to any finite subset
. Assume that to any finite subset , a choice function
, a choice function  is given, which attaches an element of
is given, which attaches an element of  to each element
to each element 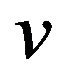 of
of :
: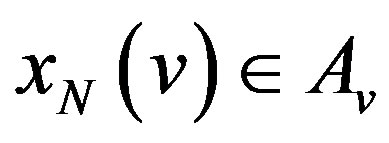 . Then there exists a choice function
. Then there exists a choice function  defined for all
defined for all 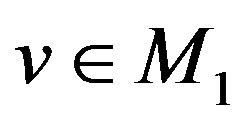 (
(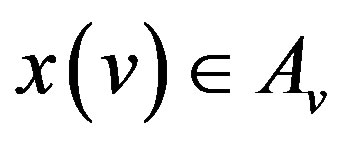 if
if ) with the following property. If
) with the following property. If 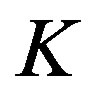 is any finite subset of
is any finite subset of , then there exists a finite subset
, then there exists a finite subset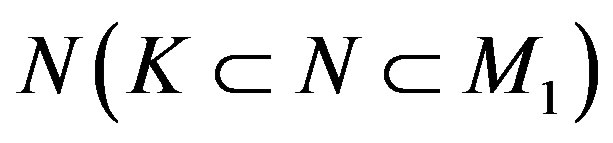 , such that, as far as
, such that, as far as 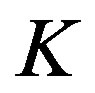 is concerned, the function
is concerned, the function 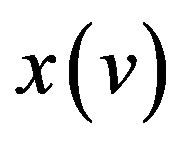 coincides with
coincides with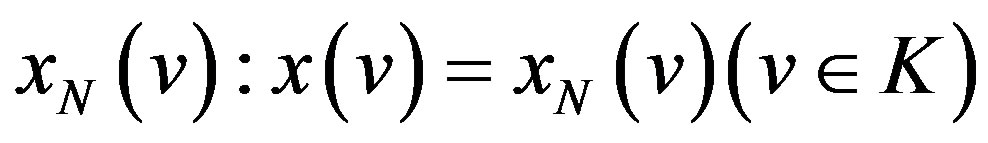 .
.
Theorem 1.1 ([2]) Let  be a positive integer, and let the graph
be a positive integer, and let the graph  have the property that any finite subgraph is
have the property that any finite subgraph is  -colorable. Then
-colorable. Then  is
is  -colorable itself.
-colorable itself.
Theorem 1.1 allows us to look for the maximum number of colors needed for the finite subsets. It is obvious that 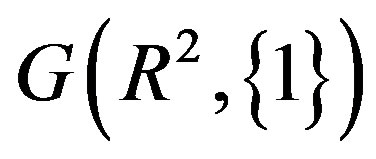 is not a trivial graph. Therefore
is not a trivial graph. Therefore
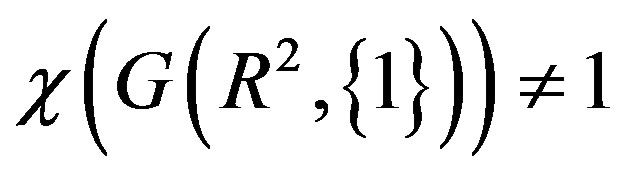 . The presence of at least one edgeviz., between (0,0) and (1,1) in
. The presence of at least one edgeviz., between (0,0) and (1,1) in  conveys the information that
conveys the information that . Similarly, the presence of a clique of size 3, viz.,
. Similarly, the presence of a clique of size 3, viz.,  with vertices at
with vertices at
(0,0), 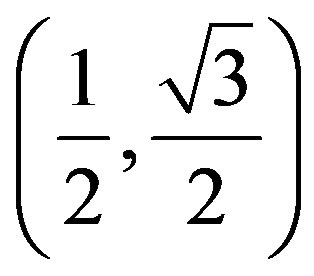 , (1,1) shows that
, (1,1) shows that
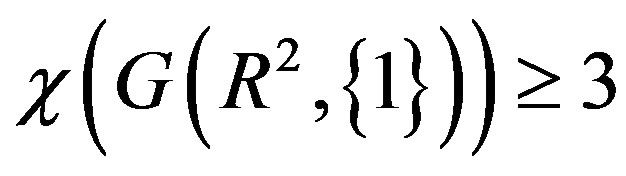 .
.
Moreover, it is a fact that four points in the Euclidean two dimensional plane cannot have pairwise odd integer distances. Therefore, a clique of size 4, viz.,  cannot be an induced subgraph of
cannot be an induced subgraph of . But it will be quite interesting to find the coordinates of a unit distance finite subgraph of
. But it will be quite interesting to find the coordinates of a unit distance finite subgraph of  such that
such that 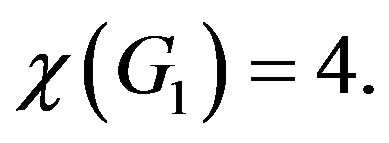 The Moser Spindle graph in Figure 1 with a chromatic 4-coloring is a good example to deduce that
The Moser Spindle graph in Figure 1 with a chromatic 4-coloring is a good example to deduce that
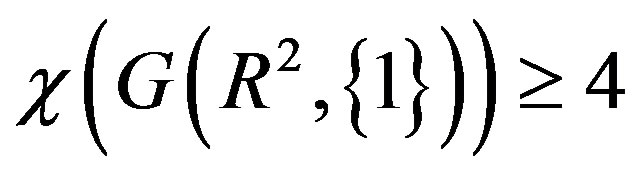 .
.
It is interesting to note that so far no unit distance graph that requires exactly five colors are known. Falconer [3] showed that if the color classes form meaurable sets of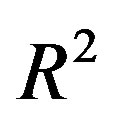 , then at least five colors are needed. Since the construction of non measurable sets requires the axiom of choice, we might have the answer turn out to depend on whether or not we accept the axiom of choice. We can tile the plane with hexagons to obtain a proper 7-coloring of the graph. The result is originally due to Hadwiger and Debrunner [4]. So
, then at least five colors are needed. Since the construction of non measurable sets requires the axiom of choice, we might have the answer turn out to depend on whether or not we accept the axiom of choice. We can tile the plane with hexagons to obtain a proper 7-coloring of the graph. The result is originally due to Hadwiger and Debrunner [4]. So .
.
See Figures 2 and 3 for the lower and upper bounds respectively. Despite the age of this problem, very little progress has been made since the initial bounds on 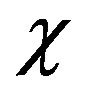 were discovered shortly after the problem’s creation. This fact is a testament to the difficulty of the problem and in the absence of progress on the main problem, a number of restricted versions and related questions have been studied. We study here the open problem of characterizing the class 4 sets mentioned in the problem for the prime distance graph whose vertex set is
were discovered shortly after the problem’s creation. This fact is a testament to the difficulty of the problem and in the absence of progress on the main problem, a number of restricted versions and related questions have been studied. We study here the open problem of characterizing the class 4 sets mentioned in the problem for the prime distance graph whose vertex set is 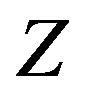 and the distance set
and the distance set  is a subset of not only primes
is a subset of not only primes 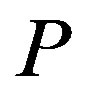 but are also they are a special set of primes. The authors have already made some progress in [5-11].
but are also they are a special set of primes. The authors have already made some progress in [5-11].
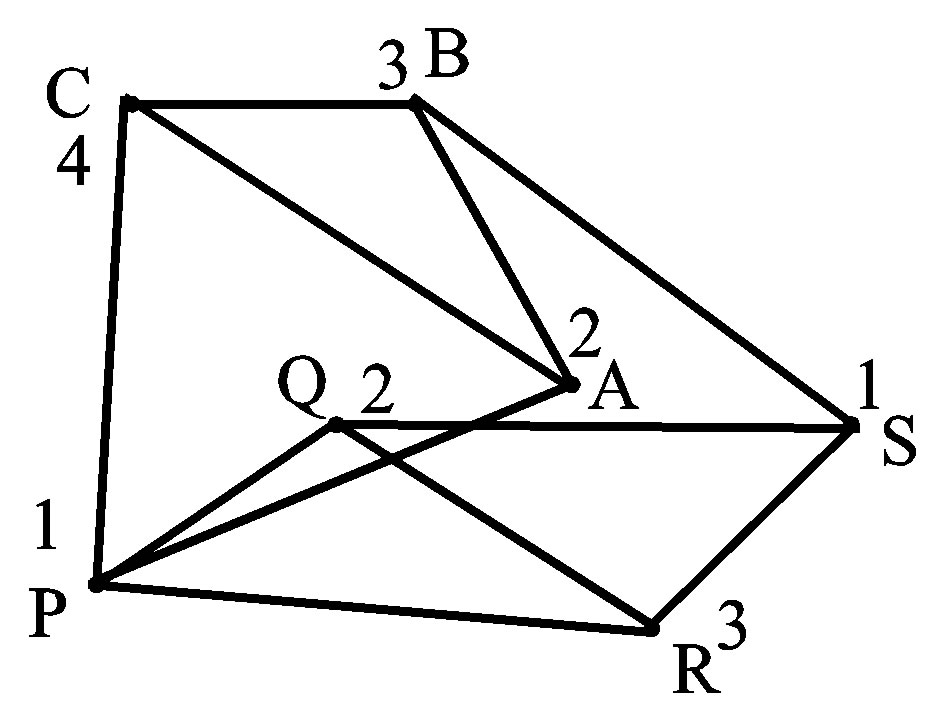
Figure 2. The moser spindle.
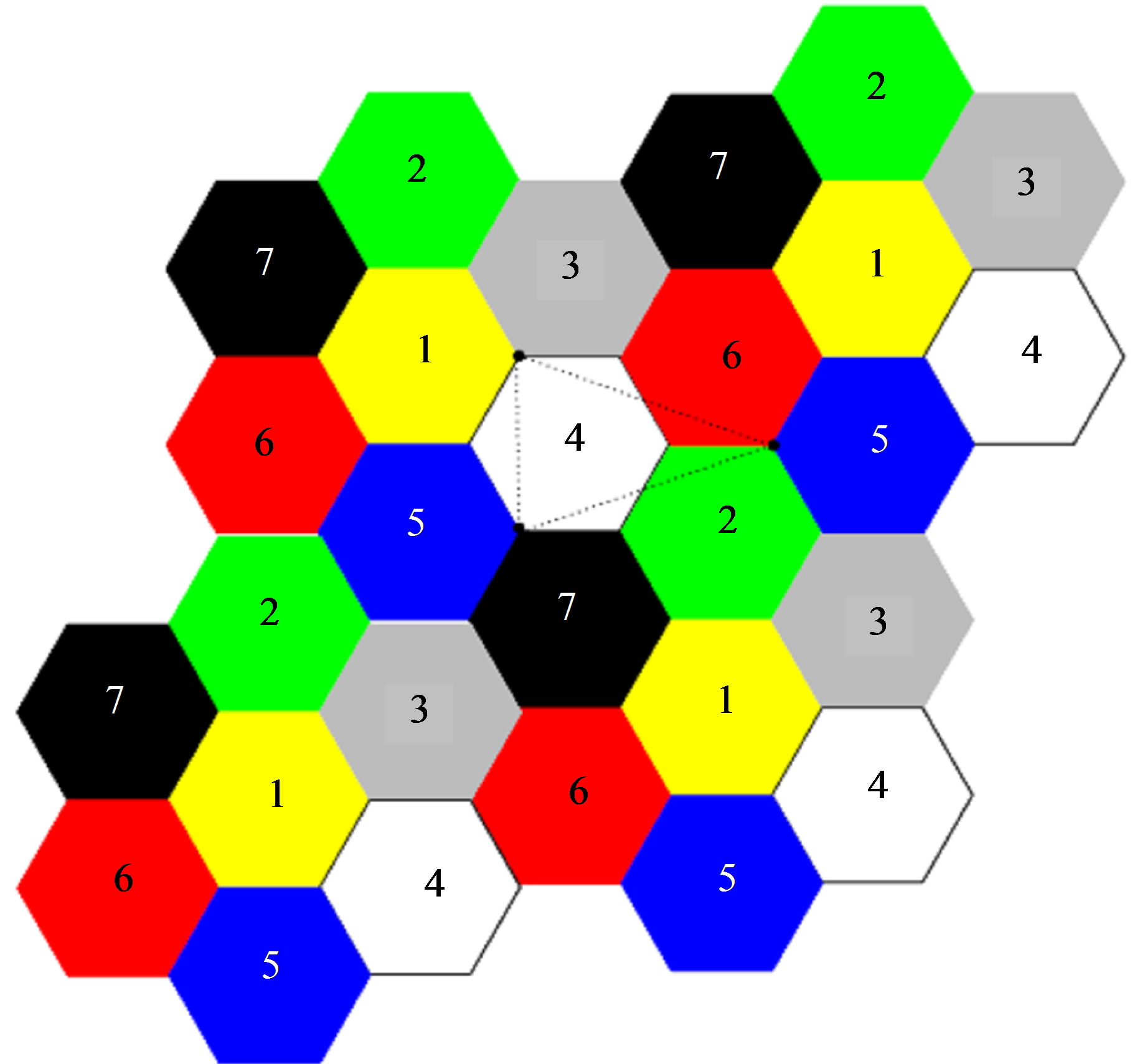
Figure 3. The hexagonal 7 coloring.
2. Prime Distance Graph
A prime distance graph is a graph 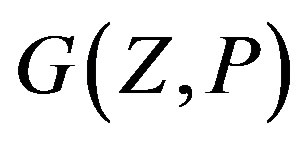 with the set of integers as vertex set and with an edge joining two vertices
with the set of integers as vertex set and with an edge joining two vertices  and
and 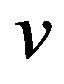 if and only if
if and only if  where
where 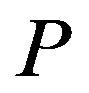 is the set of all prime numbers.
is the set of all prime numbers.
By a chromatic subgraph of a graph  we mean a minimal subgraph of
we mean a minimal subgraph of  with the same chromatic number as
with the same chromatic number as .What class of graphs will include a chromatic subgraph of
.What class of graphs will include a chromatic subgraph of  for
for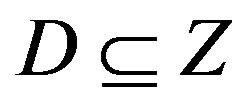 ?
?
A graph 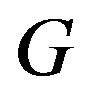 is color critical if its only chromatic subgraph is
is color critical if its only chromatic subgraph is  itself. For any positive integer
itself. For any positive integer , let
, let  be the graph comprising
be the graph comprising  distinct vertices
distinct vertices  and
and 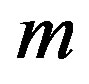 distinct subgraphs
distinct subgraphs  each of which is a copy of
each of which is a copy of 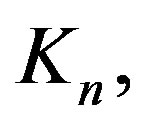 (Where
(Where 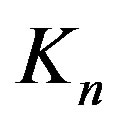 is the complete graph on n vertices) such that
is the complete graph on n vertices) such that  is adjacent to
is adjacent to  and each vertex of
and each vertex of  is adjacent to
is adjacent to 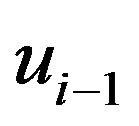 and
and 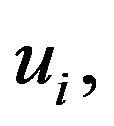 for
for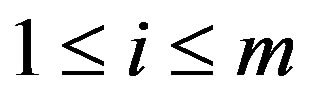 .
.
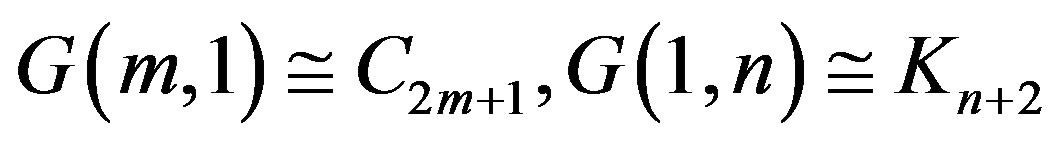 where
where 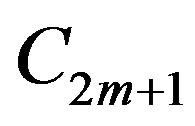 is the cycle on
is the cycle on  vertices.
vertices.
Certain Known Results
Lemma 2.1 ([12]) For any positive integers 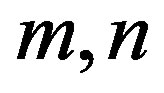 the graph
the graph 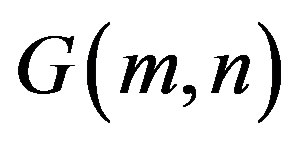 is color critical with
is color critical with .
.
Theorem 2.1 ([13])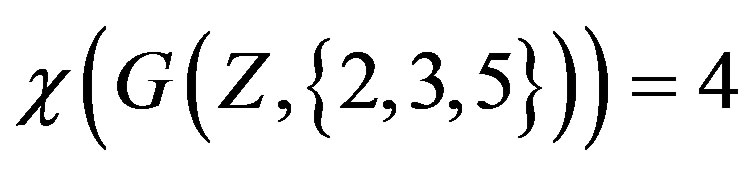 and hence
and hence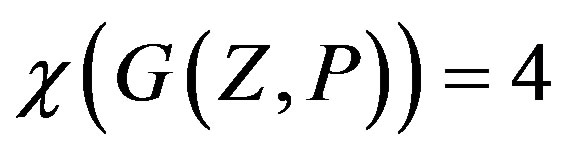 .
.
Proof. Let each integer 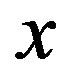 be assigned a color class
be assigned a color class 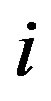 precisely when
precisely when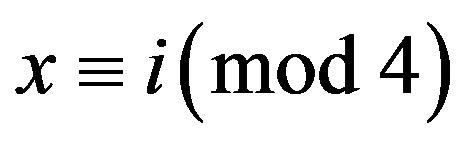 , for
, for  Since integers assigned to the same color differ by a multiple of 4, they are not adjacent in
Since integers assigned to the same color differ by a multiple of 4, they are not adjacent in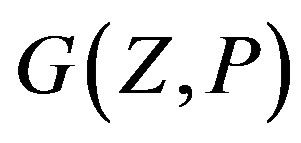 , so
, so
 .
.
Since  and
and  is monotone, we have
is monotone, we have
 .
.
But as 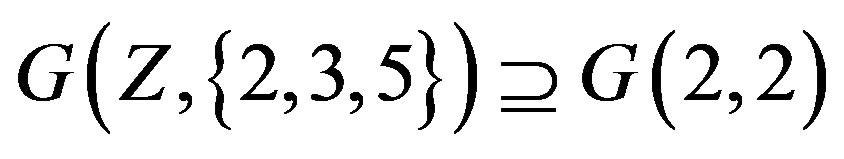 we have
we have
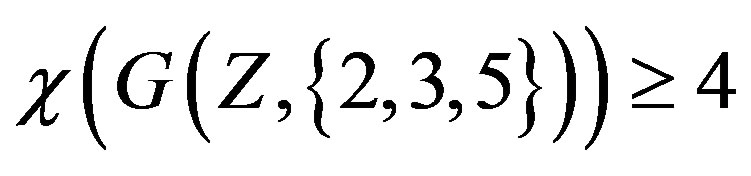
where 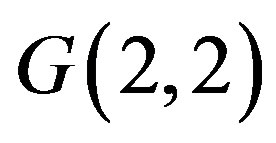 is shown in the Figure 4 determined by the vertices
is shown in the Figure 4 determined by the vertices  and the subgraphs
and the subgraphs  with vertex sets
with vertex sets  and
and  respectively. The proof now follows from the Lemma 2.1.
respectively. The proof now follows from the Lemma 2.1.
In view of Theorem 2.1, we can allocate the subsets  of
of 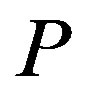 to four classes, according as
to four classes, according as 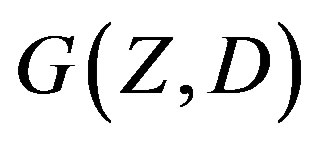 has chromatic number 1, 2, 3 or 4. Obviously empty set is the only member of class 1 and every singleton subset is in class 2.
has chromatic number 1, 2, 3 or 4. Obviously empty set is the only member of class 1 and every singleton subset is in class 2.
Lemma 2.2 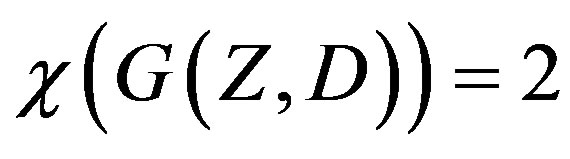 if
if  consists only of odd integers.
consists only of odd integers.
Proof. Partition  into two sets with
into two sets with
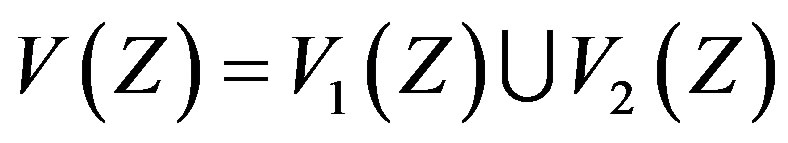
such that an integer  if and only if
if and only if  . Now as the elements of
. Now as the elements of 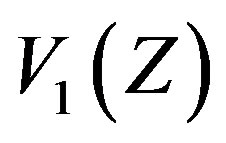 are even and the elements of
are even and the elements of 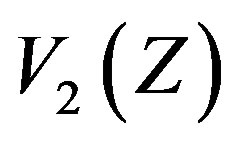 are odd we find that
are odd we find that 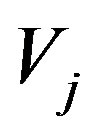 is an independent set for
is an independent set for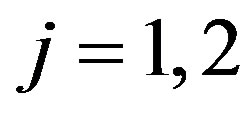 . Therefore
. Therefore  is bipartite and hence
is bipartite and hence . See Figure 5, where = indicates the presence of an edge between any two vertices.
. See Figure 5, where = indicates the presence of an edge between any two vertices.
Preposition 1 ([14]) If  is finite and the greatest common divisor of the elements of
is finite and the greatest common divisor of the elements of  is 1 then
is 1 then
(a)  if all
if all  are odd,
are odd,
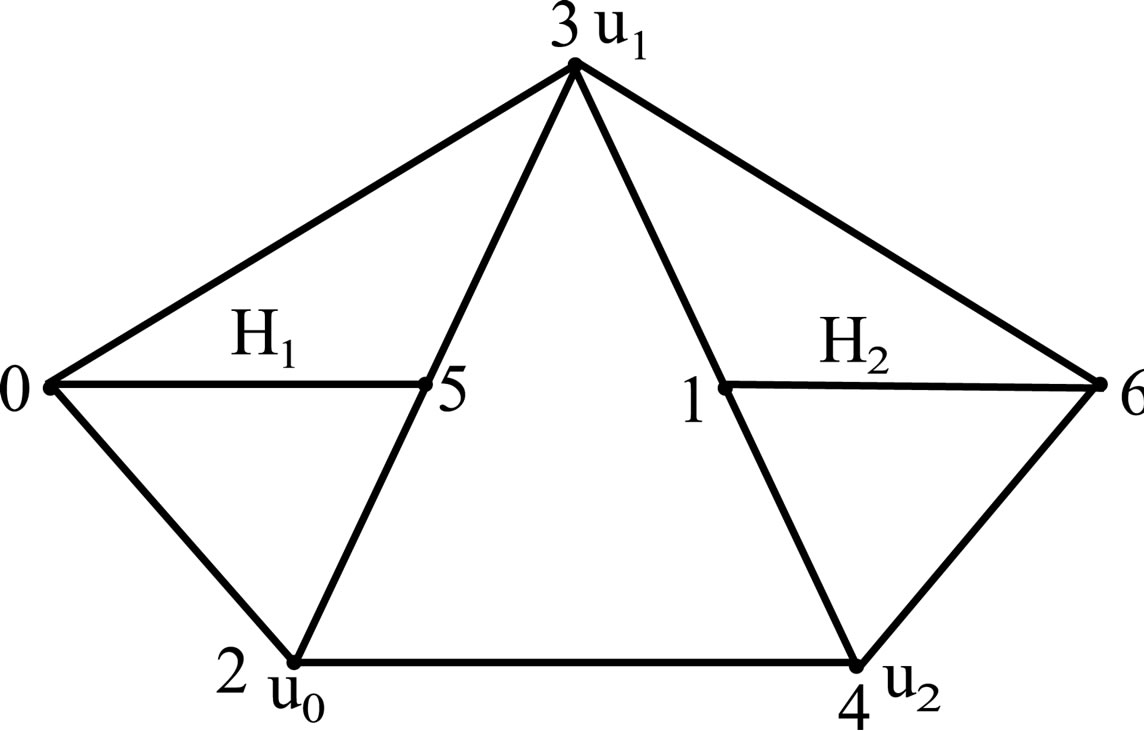
Figure 4. In the figure  and
and 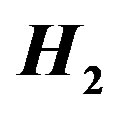 are isomorphic to
are isomorphic to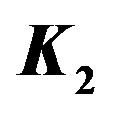 .
.
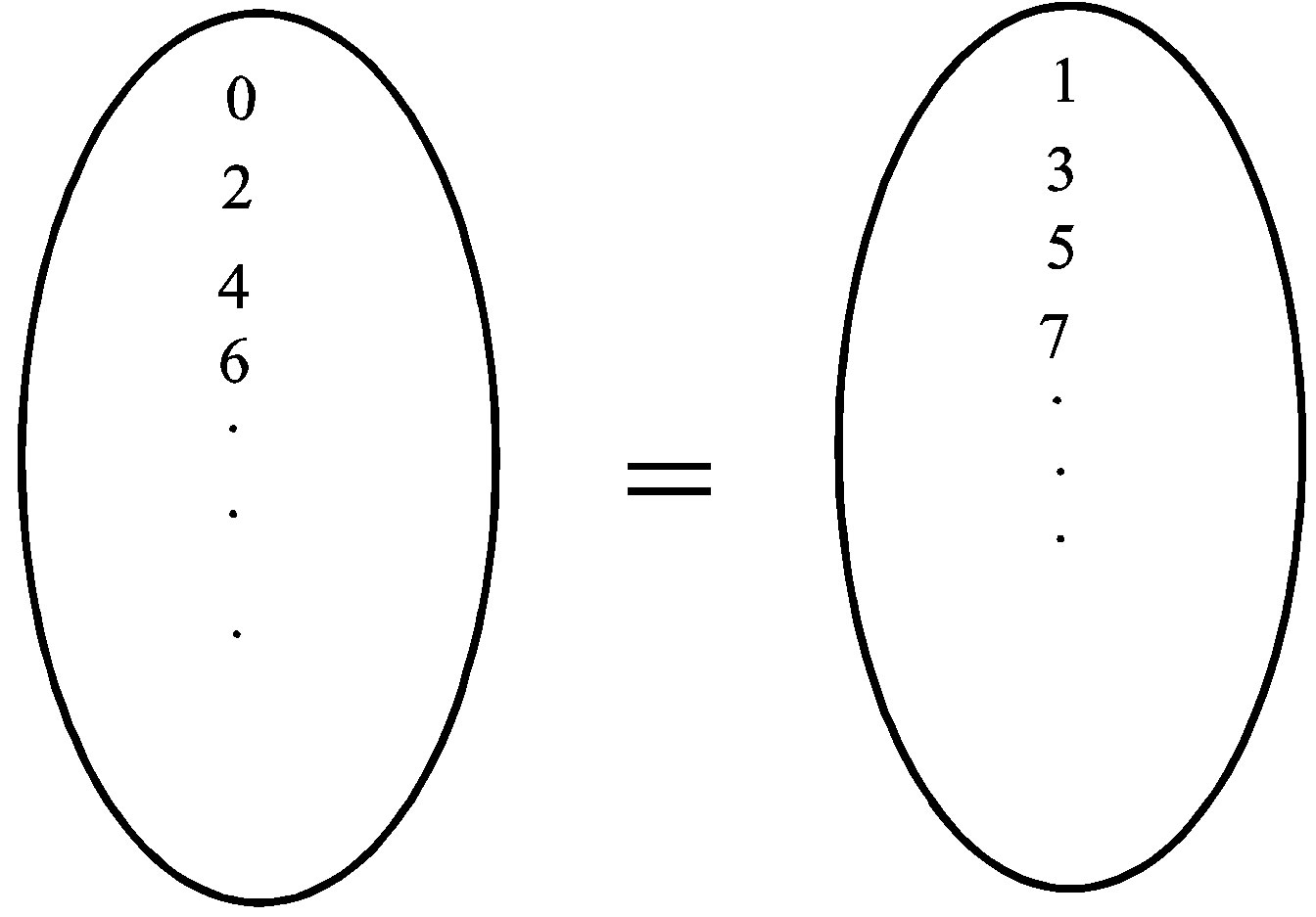
Figure 5. = indicates the presence of an edge between any two vertices of V1(Z) and V2(Z).
(b)  if no distance element is divisible by 3(c)
if no distance element is divisible by 3(c)  if no distance element is divisible by 3 and at least one distance element is even.
if no distance element is divisible by 3 and at least one distance element is even.
Lemma 2.3 If  contains no multiple of a fixed positive integer
contains no multiple of a fixed positive integer , then
, then 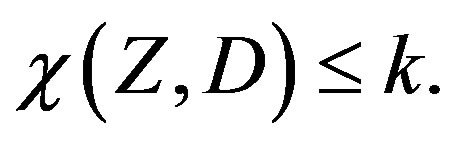
Proof. Color each vertex 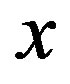 in
in  by
by 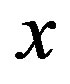 mod
mod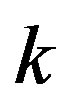 . Since
. Since 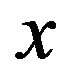 and
and  have the same color if and only if
have the same color if and only if  is a multiple of
is a multiple of , but
, but  contains no multiple of
contains no multiple of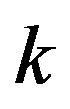 , this is a proper
, this is a proper 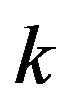 -coloring.
-coloring.
For simplicity, we assume that  in the rest of this section. If
in the rest of this section. If , then it is not hard to see that
, then it is not hard to see that . For the case of
. For the case of , where
, where  and
and 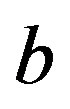 are relatively prime, and so either they are both odd or they are of opposite parity.
are relatively prime, and so either they are both odd or they are of opposite parity.
Theorem 2.2 If  and
and  are relatively prime positive odd integers, then
are relatively prime positive odd integers, then 
Proof. The theorem follows immediately from Lemma 2.3 and the fact that  for any nonempty
for any nonempty .
.
Theorem 2.3 ([13]) Let 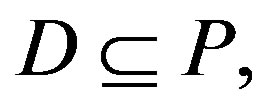 with
with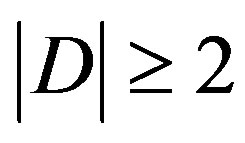 . Then
. Then  may be classified as follows:
may be classified as follows:
(a)  is in class 2 if
is in class 2 if ; otherwise
; otherwise  is in class 3 or 4.
is in class 3 or 4.
(b) If 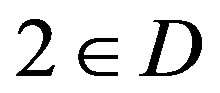 and
and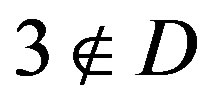 , then
, then  is in class 3.
is in class 3.
(c) If , then
, then  is in class 3.
is in class 3.
(d) If , then
, then  is in class 3.
is in class 3.
(e) If  or
or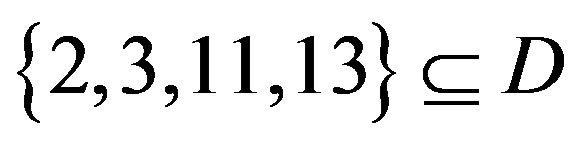 , then
, then  is in class 4.
is in class 4.
Theorem 2.4 ([13]) For any prime 
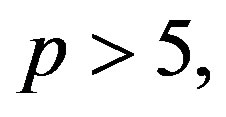 is in class 3.
is in class 3.
Lemma 2.4 ([15]) There exists only a finite number of sets 
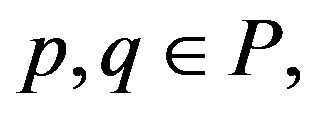
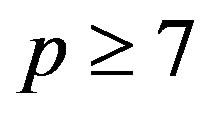 and
and 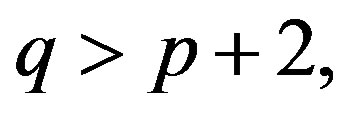 with
with 
Theorem 2.5 ([15]) Let 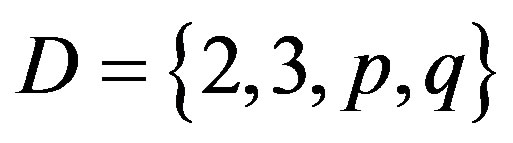 be a set of primes with
be a set of primes with 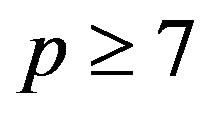 and
and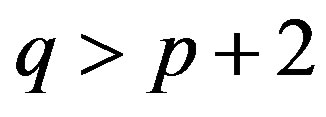 . Then
. Then 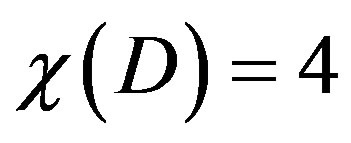 holds if and only if
holds if and only if
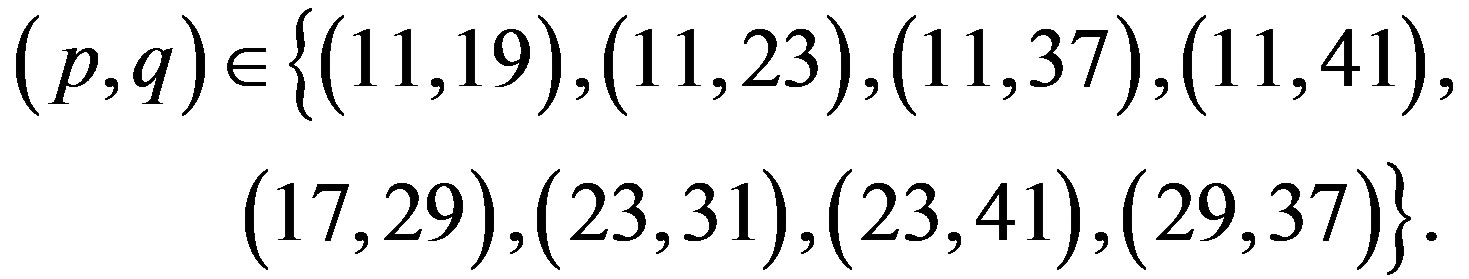
The proofs of Lemma 2.4 and Theorem 2.5 are available in [15]. Moreover, the authors M. Voigt and H. Walther have shown that there are exactly eight pairs of primes 
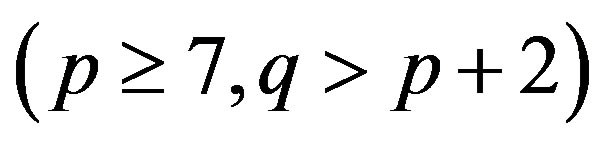 with
with 
Theorem 2.6 ([16]) Let  with
with 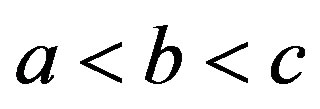 and
and  Then
Then
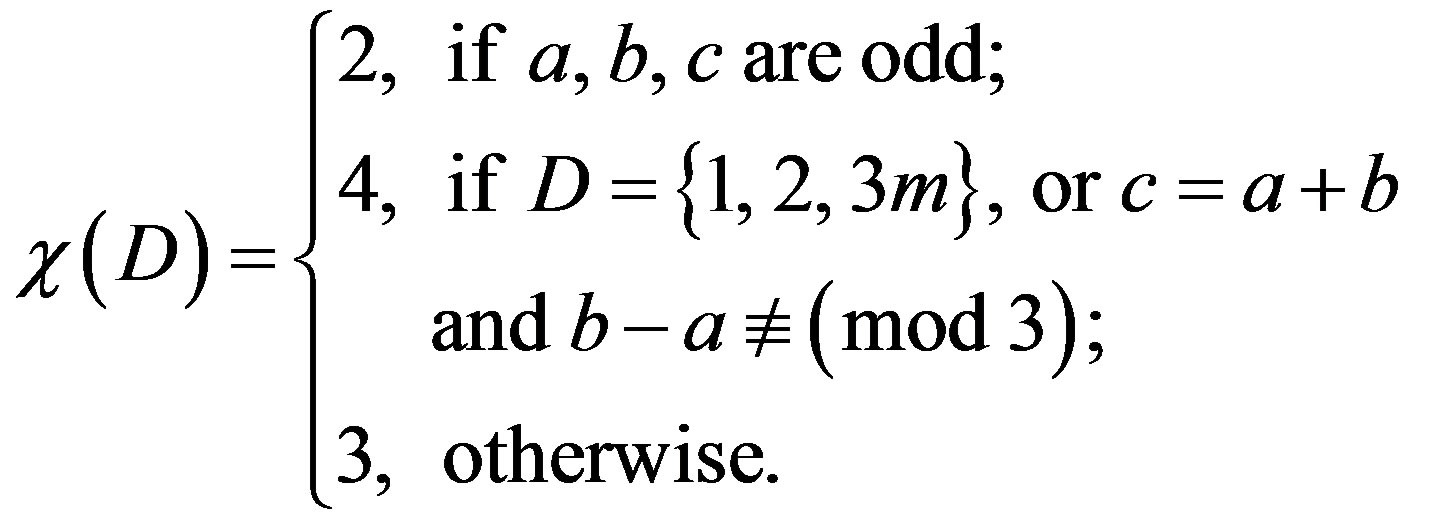
3. Some Special Set of Prime Numbers
Consider the following interesting set of prime numbers namely Additive Primes, Deletable Primes, WedderburnEtherington Number Primes, Euclid-Mullin Sequence Primes, Motzkin Primes, Schröder Primes, Catalan Primes, Non-generous Primes, Pell Primes, Primes of Binary Quadratic Form, Primeval Primes, Smarandache-Wellin Primes, Highly Cototient Number Primes, Annihilating Primes, Euclid primes, Fortunate Primes, SchröderHipparchus Number primes, Gaussian Primes, Mersenne Primes, Odd Primes, Primorial Primes, Proth Primes, Regular Primes, Self Primes, Solinas Primes, Super Primes, Delannoy Number Primes, Unique Primes, and Wagstaff Primes. For the definitions of these set of primes refer [17]. However, the existence of an interesting mathematical process that logically leads to the precise definition of an Annihilating prime we mention the same here for the sake of completeness and for the ease of the readers. Each of these set of primes have certain unique properties that make them special and are found to be useful from both theoretical and practical point of view.
Annihilating Primes
Definition 3.1 ([18]) For  let
let  denote the number of one-to-one sequences— these are sequences without repetitions—we can build with
denote the number of one-to-one sequences— these are sequences without repetitions—we can build with  distinct objects.
distinct objects.
 (= the empty sequence),
(= the empty sequence),  ,
, 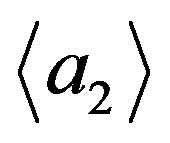 ,
,  ,
,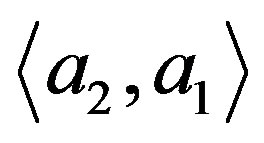 .
.
Hence, . Of course, it is easy to find a general expression for
. Of course, it is easy to find a general expression for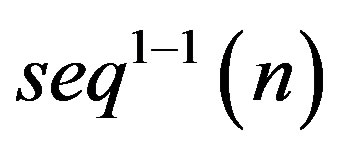 . Since there are
. Since there are 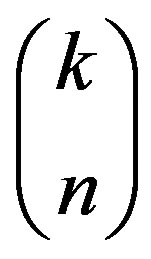
possible ways to choose  objects from a set of
objects from a set of 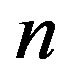 (distinct) objects, and since
(distinct) objects, and since  (distinct) objects give rise to
(distinct) objects give rise to  permutations, we get the following Lemma.
permutations, we get the following Lemma.
Lemma 3.1  Also the next representation for
Also the next representation for 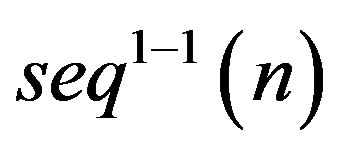 is elementary.
is elementary.
Lemma 3.2 For all positive  we have
we have 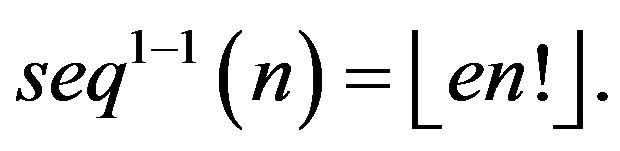
Remark: For 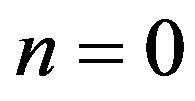 the formula does not hold, since
the formula does not hold, since .
.
Proof. According to Lemma 3.1 we have
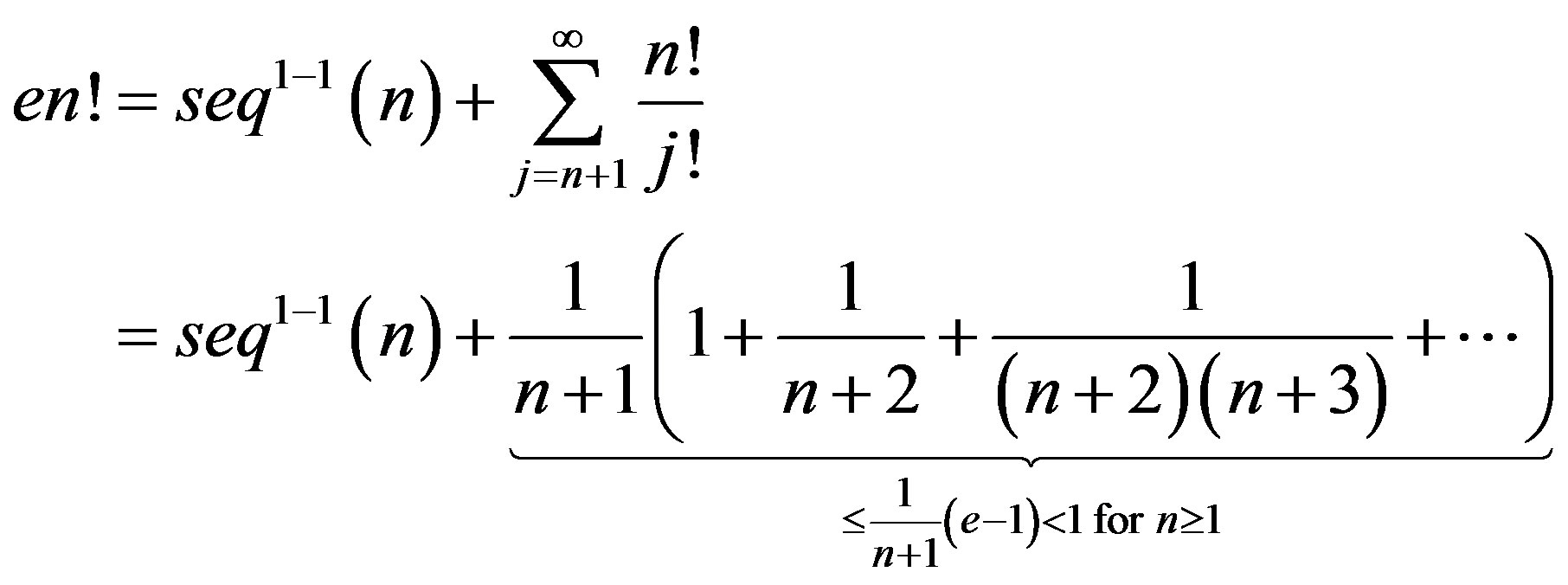
The following recursive relation for  is an immediate consequence of the second formula in Lemma 3.1.
is an immediate consequence of the second formula in Lemma 3.1.
Lemma 3.3 For all positive 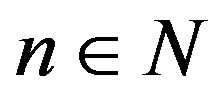 we have
we have 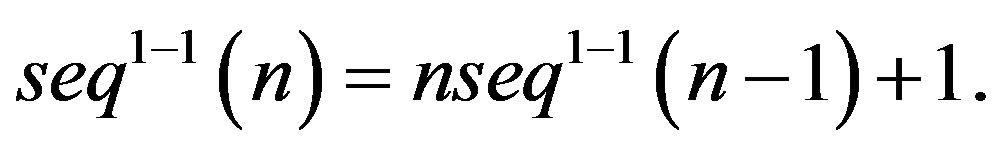 Using this formula, we finally get the following integral representation of
Using this formula, we finally get the following integral representation of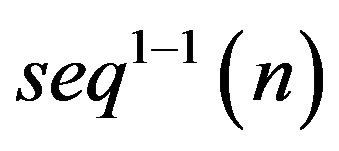 .
.
Lemma 3.4 For all  we have
we have
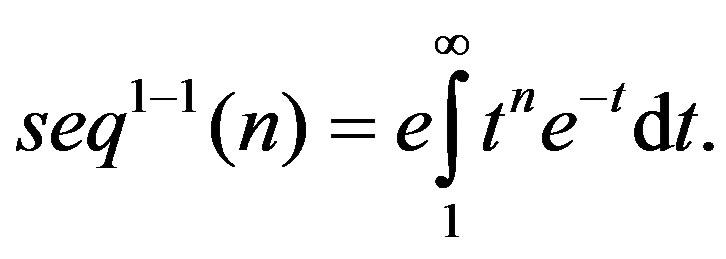
Notation: Throughout this text we adopt the standard notation 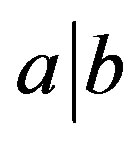 to express that
to express that  divides
divides  for
for 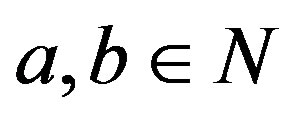 . Moreover, if
. Moreover, if 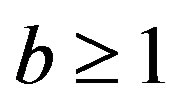 then
then
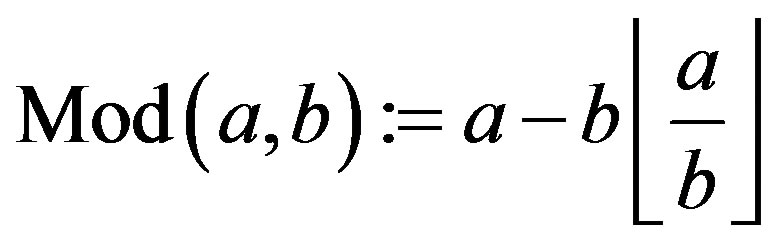
denotes the reminder of the division of  by
by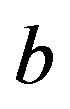 ; and
; and 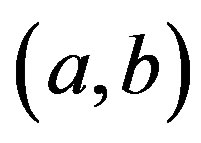 denotes the greatest common divisor of
denotes the greatest common divisor of  and
and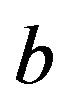 .
.
We start our investigation on divisibility properties of 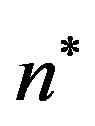 with a simple fact which has first been proved in [19].
with a simple fact which has first been proved in [19].
Lemma 3.5 For natural numbers , the following implication holds: If
, the following implication holds: If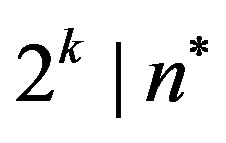 , then
, then 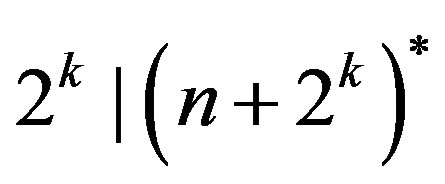
and 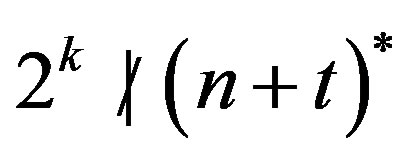 for any
for any  with
with 
Definition 3.2 If 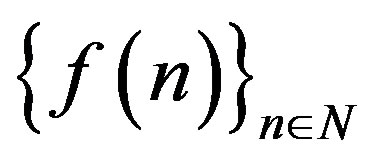 is a sequence of natural numbers, we define its shadow to be the sequence
is a sequence of natural numbers, we define its shadow to be the sequence  given by
given by  where
where
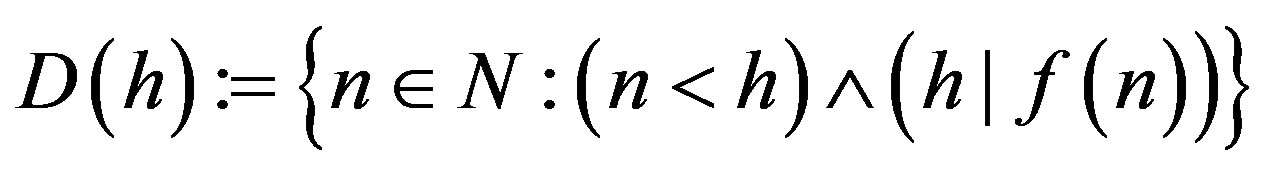
are the shadow sets of the sequence 
The shadow  counts the sequence entries
counts the sequence entries  which are divisible by
which are divisible by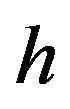 . So, the shadow measures (to a certain extent) how “divisible” the entries of the sequence
. So, the shadow measures (to a certain extent) how “divisible” the entries of the sequence 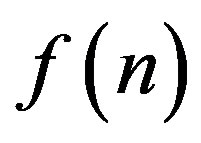 are: For example, if only prime numbers occur in the sequence, then its shadow will reflect this fact by being small. If the entries of
are: For example, if only prime numbers occur in the sequence, then its shadow will reflect this fact by being small. If the entries of 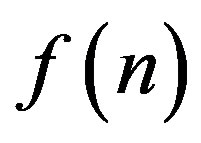 have many divisors, the shadow will typically be large.
have many divisors, the shadow will typically be large.
If 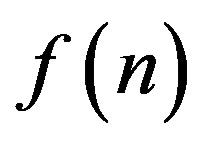 is an arithmetic sequence of first order, then its shadow is periodic, and for the shadow of Euler’s
is an arithmetic sequence of first order, then its shadow is periodic, and for the shadow of Euler’s 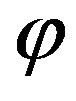 -function we have
-function we have 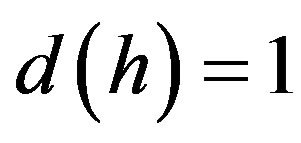 for all
for all 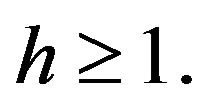
Example: If for a function  there exists an
there exists an  such that for all
such that for all 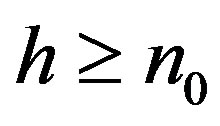 we have
we have  then for all
then for all 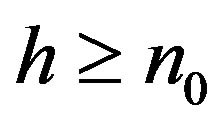 we have
we have . Vice versa, if
. Vice versa, if 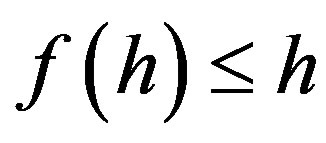 for all
for all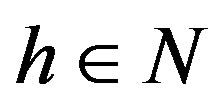 , then
, then  equals the number of zeros in
equals the number of zeros in . Hence, it is easy to construct different functions which have the same shadow:
. Hence, it is easy to construct different functions which have the same shadow:
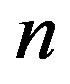 0 1 2 3 4 5 6 7···
0 1 2 3 4 5 6 7···
 0 1 2 3 4 5 6 7···
0 1 2 3 4 5 6 7···
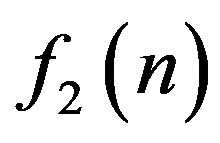 0 1 1 2 3 4 5 6···
0 1 1 2 3 4 5 6···
 0 1 1 1 2 3 4 5···
0 1 1 1 2 3 4 5···
shadow 0 1 1 1 1 1 1 1···
Definition 3.3 A sequence 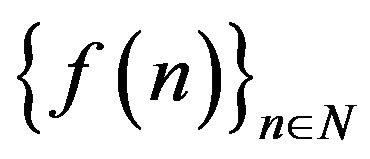 is said to have the reduction property, if for all
is said to have the reduction property, if for all 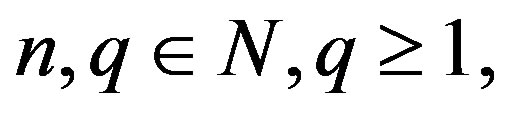 we have,
we have, 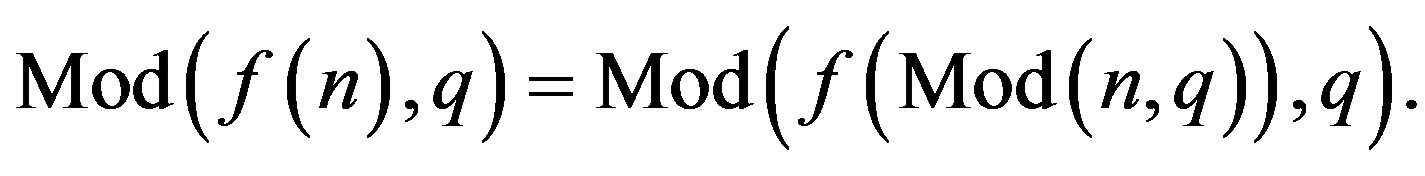
Lemma 3.6 The sequence 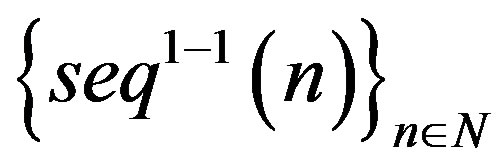 has the reduction property.
has the reduction property.
Lemma 3.7 The shadow 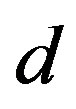 of a sequence
of a sequence  which has the reduction property is multiplicative, i.e. if
which has the reduction property is multiplicative, i.e. if , then
, then .
.
As an immediate consequence we get the following:
Corollary 1 If 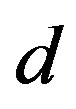 is the shadow of
is the shadow of 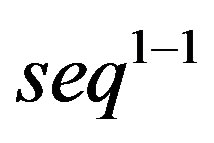 and if
and if
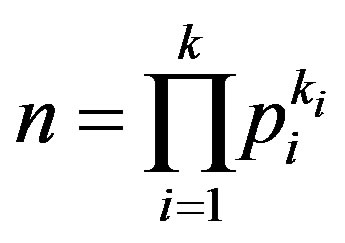
is the prime decomposition of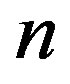 , then
, then
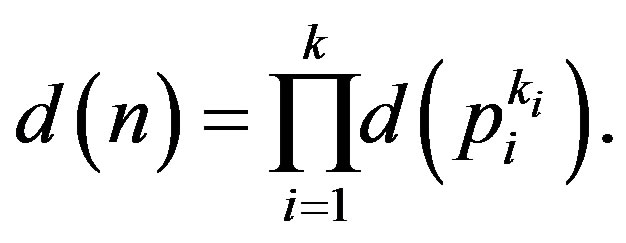
Therefore, the shadow 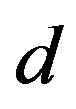 of
of 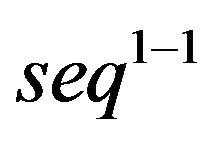 is fully determined by its values on the powers of prime numbers. But what can we say about
is fully determined by its values on the powers of prime numbers. But what can we say about  for
for  prime?
prime?
By the reduction property, all elements 
must be of the form 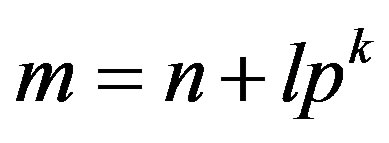 for some
for some 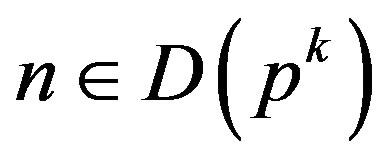
and some . Hence, we get inductively that if
. Hence, we get inductively that if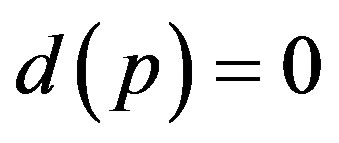 , then
, then 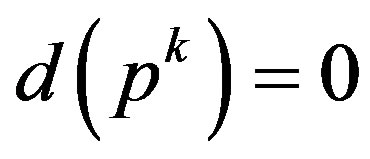 for all positive
for all positive 
Definition 3.4 A prime number 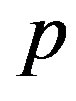 with
with 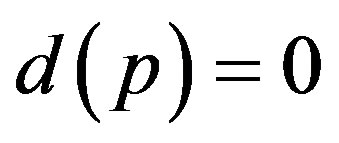 is called annihilating.
is called annihilating.
Preposition 2 If  is divisible by an annihilating prime, then
is divisible by an annihilating prime, then 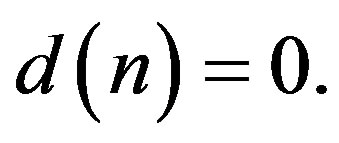
Annihilating primes are primes such that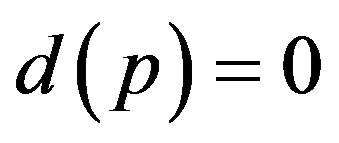 , where
, where 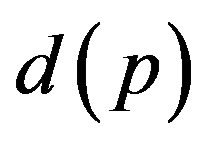 is the shadow of a sequence of natural numbers. First few such primes are: 3, 7, 11, 17, 47, 53, 61, ···
is the shadow of a sequence of natural numbers. First few such primes are: 3, 7, 11, 17, 47, 53, 61, ···
4. Chromatic Number of Certain Prime Distance Graphs
Here we compute the chromatic number of the distance graph: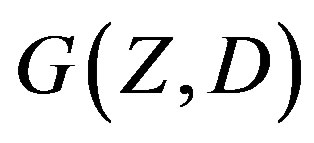 , when
, when  is a set/subset of any of the above listed primes.
is a set/subset of any of the above listed primes.
Theorem 4.1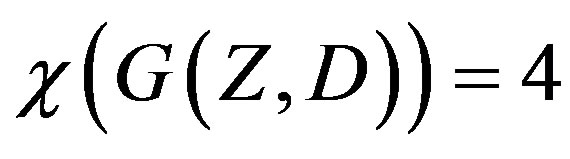 , when
, when  is a finite/ infinite set/subset as the case may be of WedderburnEtherington Number Primes.
is a finite/ infinite set/subset as the case may be of WedderburnEtherington Number Primes.
Proof. Let  denote the set of Wedderburn-Etherington Number Primes. Note that in
denote the set of Wedderburn-Etherington Number Primes. Note that in , the set of primes
, the set of primes  appears as a proper subset. By Lemma 2.4 and Theorem 2.5, the set of primes
appears as a proper subset. By Lemma 2.4 and Theorem 2.5, the set of primes 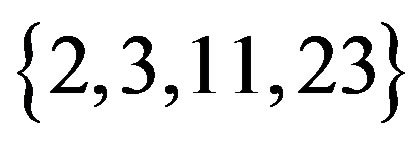 is one of the eight sets of chromatic number 4 class. So
is one of the eight sets of chromatic number 4 class. So
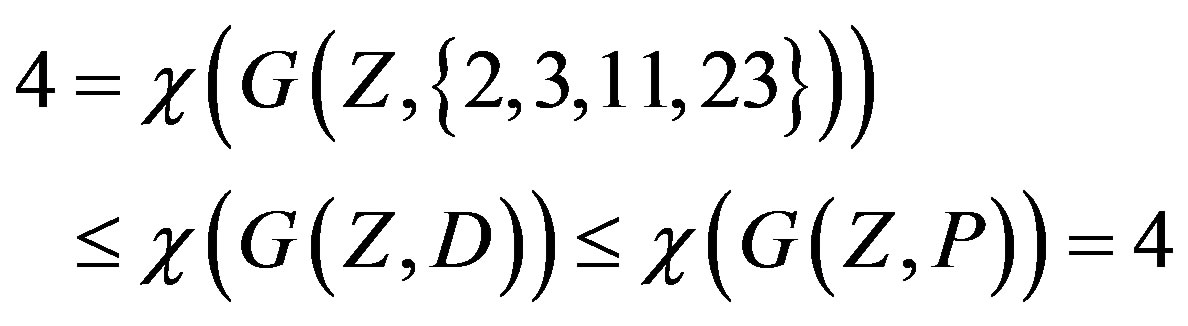
as .
.
Theorem 4.2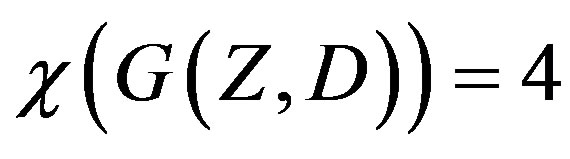 , when
, when  is a finite/ infinite set/subset as the case may be of Additive Primes, Deletable Primes, and Euclid-Mullin sequence primes.
is a finite/ infinite set/subset as the case may be of Additive Primes, Deletable Primes, and Euclid-Mullin sequence primes.
Proof. Let  be the set of Additive primes/Deletable primes/ Euclid-Mullin sequence primes. As the set of primes
be the set of Additive primes/Deletable primes/ Euclid-Mullin sequence primes. As the set of primes  is a proper subset of
is a proper subset of , by Theorem 1.1 and Theorem 2.1
, by Theorem 1.1 and Theorem 2.1

as .
.
Theorem 4.3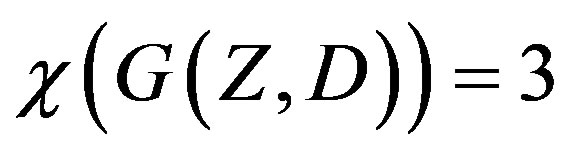 , when
, when  is a finite/ infinite set/subset as the case may be of 1) Motzkin primes, 2) Catalan primes, 3) Schröder primes, 4) Nongenerous primes, 5) Pell primes, 6) Primeval primes, 7) Primes of binary quadratic form, 8) Smarandache-Wellin primes, and 9) Highly Cototient number primes.
is a finite/ infinite set/subset as the case may be of 1) Motzkin primes, 2) Catalan primes, 3) Schröder primes, 4) Nongenerous primes, 5) Pell primes, 6) Primeval primes, 7) Primes of binary quadratic form, 8) Smarandache-Wellin primes, and 9) Highly Cototient number primes.
Proof. Let  denote the set of any one of these special class of prime numbers listed in the theorem. All these set of primes have a unique property that an even prime integer 2 is in
denote the set of any one of these special class of prime numbers listed in the theorem. All these set of primes have a unique property that an even prime integer 2 is in  but the odd prime integer 3 is not appearing in
but the odd prime integer 3 is not appearing in . So by Theorem 2.3(b) and Preposition 1(c),
. So by Theorem 2.3(b) and Preposition 1(c),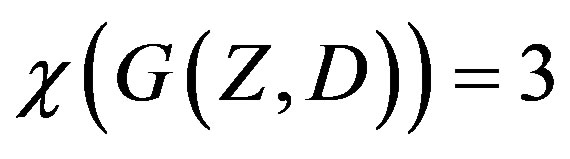 .
.
Theorem 4.4 , when
, when  is a finite/ infinite set/subset as the case may be of 1) Euclid primes, 2) Fortunate primes, 3) Schröder-Hipparchus Number primes, 4) Gaussian primes, 5) Mersenne primes, 6) Odd primes, 7) Primorial primes, 8) Proth primes, 9) Regular primes, 10) Self primes, 11) Solinas primes, 12) Super primes, 13) Delannoy Number primes, 14) Unique primes, 15) Wagstaff primes, and 16) Annihilating primes.
is a finite/ infinite set/subset as the case may be of 1) Euclid primes, 2) Fortunate primes, 3) Schröder-Hipparchus Number primes, 4) Gaussian primes, 5) Mersenne primes, 6) Odd primes, 7) Primorial primes, 8) Proth primes, 9) Regular primes, 10) Self primes, 11) Solinas primes, 12) Super primes, 13) Delannoy Number primes, 14) Unique primes, 15) Wagstaff primes, and 16) Annihilating primes.
Proof. Let  denote the set of any one of these special class of prime numbers listed in the theorem. All these special class of primes have a unique property that
denote the set of any one of these special class of prime numbers listed in the theorem. All these special class of primes have a unique property that  does not contain the even prime integer 2 but
does not contain the even prime integer 2 but  has an odd prime integer 3. So by Theorems 2.2 and 2.3(a),
has an odd prime integer 3. So by Theorems 2.2 and 2.3(a),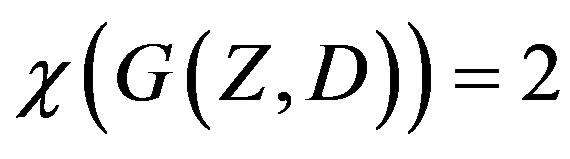 .
.
Conclusion
A complete characterization of class three sets and class four sets are available in the literature when the cardinality of the distance subset  of
of  are either 3 or 4. However when the cardinality of
are either 3 or 4. However when the cardinality of  is more than 4 only a little is known. So in this aspect Theorem 4.1, Theorem 4.2 and Theorem 4.3 makes some progress towards the complete characterization of class three and class four sets. Moreover, Theorem 4.4 brings out certain special classes of prime numbers with membership in class 2 category.
is more than 4 only a little is known. So in this aspect Theorem 4.1, Theorem 4.2 and Theorem 4.3 makes some progress towards the complete characterization of class three and class four sets. Moreover, Theorem 4.4 brings out certain special classes of prime numbers with membership in class 2 category.
5. Acknowledgements
This research is carried out with the financial grant and support of National Board for Higher Mathematics, Government of India under the grant sanction no. 2/ 48(10)/2005/R&D-II/11192/dated 26,Nov,2010.
REFERENCES
- R. Rado, “Axiomatic Treatment of Rank in Infinite Sets,” Canadian Journal of Mathematics, Vol. 1, No. 1949, 1949, pp. 337-343. doi:10.4153/CJM-1949-031-1
- N. G. de Bruijn and P. Erdos, “A Color Problem for Infinite Graphs and a Problem in the Theory of Relations,” Proceedings, Series A, Vol. 54, No. 5; Indagationes Mathematicae, Vol. 13, No. 5, 1951, pp. 371-373.
- K. J. Falconer, “The Realization of Distances in Measurable Subsets Covering Rn,” Journal of Combinatorial Theory, Series A, Vol. 31, No. 2, 1981, pp. 184-189. doi:10.1016/0097-3165(81)90014-5
- H. Hadwiger and H. Debrunner, “Combinatorial Geometry in the Plane,” Holt, Rinehart and Winston, New York, 1964.
- V. Yegnanarayanan, “On a Question Concerning Prime Distance Graphs,” Discrete Mathematics, Vol. 245, No. 1-3, February 2002, pp. 293-298. doi:10.1016/S0012-365X(01)00221-7
- V. Yegnanarayanan and A. Parthiban, “Chromatic Number of Certain Graphs,” Proceedings of International Conference on Mathematics in Engineering and Business Management, Vol. 1, Chennai, 9-11 March 2012, pp. 115- 118.
- V. Yegnanarayanan, “Chromatic Number of Graphs with Special Distance Sets, I,” Algebra and Discrete Mathematics, Accepted for Publication in January 2013, to appear.
- V. Yegnanarayanan and A. Parthiban, “The Chromatic Number of Graphs with Special Distance Sets-III,” Journal of Mathematical and Computational Science, Vol. 2, No. 5, 2012, pp. 1257-1268.
- V. Yegnanarayanan, “The Chromatic Number of Generalized Fibonacci Prime Distance Graph,” Journal of Mathematical and Computational Science, Vol. 2, No. 5, 2012, pp. 1451-1463.
- V. Yegnanarayanan and A. Parthiban, “The Chromatic Number of Graphs With Special Distance Sets-II,” Proceedings of International Conference on Mathematical Modelling and Applied Soft Computing, CIT, Vol. 1, Coimbatore, 11-13 July 2012, pp. 305-313.
- V. Yegnanarayanan and A. Parthiban, “The Chromatic Number of Graphs With Special Distance Sets-IV,” Proceeding of International Conference on Applied Mathematics and Theoretical Computer Science, Kanyakumari, 2013, to appear.
- R. B. Eggleton, P. Erdos and D. K. Skilton, “Coloring the Real Line,” Journal of Combinatorial Theory, Series B, Vol. 39, No. 1, 1985, pp. 86-100; To Erratum, Vol. 41, 1986, p. 139.
- R. B. Eggleton, P. Erdos and D. K. Skilton, “Colouring Prime Distance Graphs,” Graphs and Combinatorics, Vol. 6, No. 1, 1990, pp. 17-32. doi:10.1007/BF01787476
- A. Kemnitz and H. Kolberg, “Coloring of Integer Distance Graphs,” Discrete Mathematics, Vol. 191, No. 1-3, 1998, pp. 113-123. doi:10.1016/S0012-365X(98)00099-5
- M. Voigt and H. Walther, “Chromatic Number of Prime Distance Graphs,” Discrete Applied Mathematics, Vol. 51, No. 1-2, 1994, pp. 197-209. doi:10.1016/0166-218X(94)90109-0
- X. Zhu, “The Circular Chromatic Number of Distance Graphs with Distance Sets of Cardinality 3,” Journal of Graph Theory, Vol. 41, No. 3, 2002, pp. 195-207. doi:10.1002/jgt.10062
- en.wikipedia.org/wiki/List_of_prime_numbers
- L. Halbeisen1 and N. Hungerbuhler, “Number Theoretic Aspects of a Combinatorial Function,” 2000. www.math.uzh.ch/user/halbeis/publications/pdf/seq.pdf
- L. Halbeisen and S. Shelah, “Consequences of Arithmetic for Set Theory,” Journal of Symbolic Logic, Vol. 59, No. 1, 1994, pp. 30-40. doi:10.2307/2275247

