Open Journal of Discrete Mathematics
Vol.2 No.3(2012), Article ID:21131,5 pages DOI:10.4236/ojdm.2012.23015
Generalized Correlativity of Median Filtering Operator on Signals*
Department of Mathematics, Shanghai University, Shanghai, China
Email: wzhy@shu.edu.cn
Received April 21, 2012; revised May 28, 2012; accepted June 17, 2012
Keywords: Median Filter; Stack Filter; Generalized Correlativity
ABSTRACT
The generalized correlativity of input signal and output signal of a stack filtering operator is defined and used for numerously measuring these filtering operators’ behavior in removing noise in signals. We show that under the criterion of the generalized correlativity, of stack filtering operators the median filtering operator is optimal, which implies that this filtering operator possesses better filtering behavior than the others.
1. Introduction
The median filter was introduced in 1974 by Tukey [1], who used the moving median as a smoothing technique in time series analysis. Since then, there have been many studies on deterministic and statistical properties of median filtering operator, such as properties of roots of median filters ([2-6]), structures of recurrent sequences of median filters ([7-9]), convergence properties of a signal ([2,10-12]), and the output distribution of mediantype filters under known distributions [13]. L-filters, a generalization of median filters, were introduced [14], their output is given by a linear combination of the order statistics of the input sequence. Assuming a constant signal in white noise, the coefficients in the linear combination are chosen to minimize the output MSE for several noise distributions, i.e., the optimal design of Lfilters, and a new methodology for the design of L-filters is presented in which the L-filter coefficients are obtained by approximating the covariance matrix of the ordered samples through the use of Taylor expansion [15]. Most practical applications deal with unknown signals, which means that the noise distributions of signals are difficulty to characterize. There are cases such as in detection, and an example was given [11], which is an original two-dimensional image obtained by Dr. J. Johnson of Redstone Arsenal with an experimental laser imaging system at the far infrared wavelength of 1.2 mm. It is very difficult to characterize the noise source in the image. In these situations, the statistical methods above do not work. Therefore, a significant filtering problem is:Given a signal with some unknown noise and a filter, how do we numerically measure its filtering behavior for the signal? This problem is general and complicated. So, in this paper, we will study this problem only for stack filters.
The organization of this paper is as follows. In Section 2 we review stack filters and their threshold decomposition property, and define the generalized correlativity between of a discrete binary input signal and its output signal of stack filters. In Section 3 we prove the optimality of median filters based on the generalized correlativity in terms of stack filters. In Section 4 we give some properties of the median filtering operator to show when and how to use the filtering operator better.
2. Stack Filtering Operators and Generalized Correlativity on Signals
In this section, first we briefly review the definition of stack filters. Stack filters are a class of sliding window, nonlinear digital filters that possess the stacking property and the threshold decomposition architecture [11]. The threshold decomposition of an M-valued signal 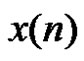 is the set of
is the set of  binary signals, called threshold signals,
binary signals, called threshold signals, 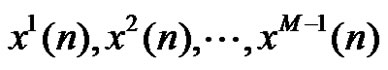 , which are defined by
, which are defined by
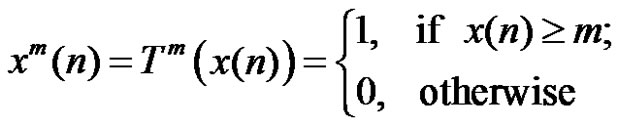
Note that the sum of the threshold signals 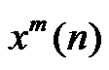 is
is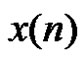 , i.e.,
, i.e.,
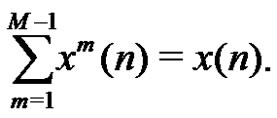
Also, the ’s are ordered, i.e.,
’s are ordered, i.e.,

This property is called the stacking property of sequences. A very important property of median filters operating within a sliding window was observed by Fitch et al. [16]: Applying a median filter to an M-valued signal is equivalent to decomposing the signal to M – 1 binary threshold signals, filtering each binary signal separately with the median filter, and then adding the binary output signals together. This is called the threshold decomposition architecture of median filters.
In the above architecture, the median operation on binary input signals reduces to a Boolean function that possesses the stacking property.
Definition 1. A 2k + 1-input Boolean function 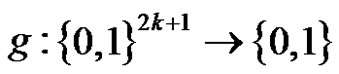 is said to possess the stacking property if whenever two input vectors x and y stack, i.e.,
is said to possess the stacking property if whenever two input vectors x and y stack, i.e.,  for each
for each , then also their outputs stack
, then also their outputs stack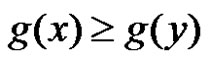 .
.
It has been shown that a Boolean function has the stacking property if and only if it can be expressed as a Boolean expression that contains no complements of input variables [11]. Such functions are called positive Boolean functions (PBF).
Definition 2. The stack filter 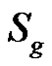 based on the PBF
based on the PBF  is defined as follows:
is defined as follows:

where
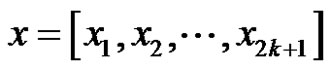
and
 .
.
Stack filters include median filters. Since stack filters possess the threshold decomposition property and the stacking property, a complete characterization of the effect of the stack filter on binary signals is sufficient to characterize the behavior of the M-valued filter. Since any 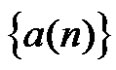 with
with 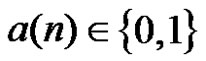 can be transformed into
can be transformed into  with
with 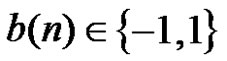 by the operation:
by the operation:  In what follows, attention will therefore be focused mainly on stack filters with binary input taking values 1 and
In what follows, attention will therefore be focused mainly on stack filters with binary input taking values 1 and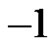 , and k is a fixed positive integer, Z is the set of integers.
, and k is a fixed positive integer, Z is the set of integers.
Thus, as Definition 1, we can definite the PBF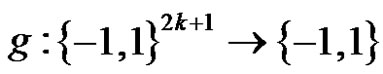 , and for each
, and for each , let, for each
, let, for each 
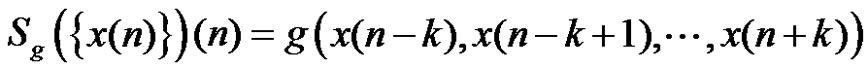
We call  a stack filtering operator with width
a stack filtering operator with width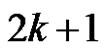 . Let
. Let 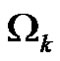 denote the set of stack filtering operators with width
denote the set of stack filtering operators with width .
.
From the definition, it is clear that for each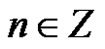 ,
, 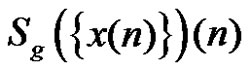 depends on
depends on 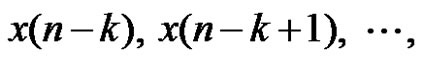
 . Therefore, we will investigate the relation between
. Therefore, we will investigate the relation between 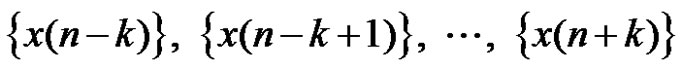 and
and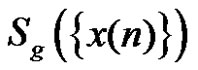 . Usually, if two sequences
. Usually, if two sequences  and
and 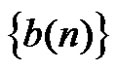 belong to
belong to , that is,
, that is,
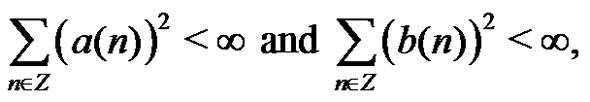
then we use
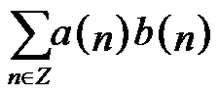
to study the correlativity of  and
and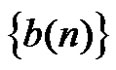 , but all
, but all  and
and do not belong to
do not belong to . Therefore, we first introduce such a window sequence with width
. Therefore, we first introduce such a window sequence with width :
: 
 satisfying
satisfying
• 
Further, we define a real sequence  satisfying
satisfying
•  for each
for each 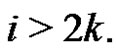
• 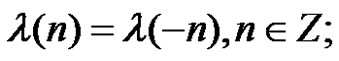
For each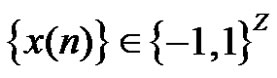 , we have
, we have

Since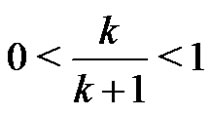 ,
, Theredore,
Theredore,
 . This is why we introduce such a real sequence.
. This is why we introduce such a real sequence.
Again we give the following definition.
Definition 3. Suppose  is a window filtering operator with width
is a window filtering operator with width . For each
. For each , let
, let
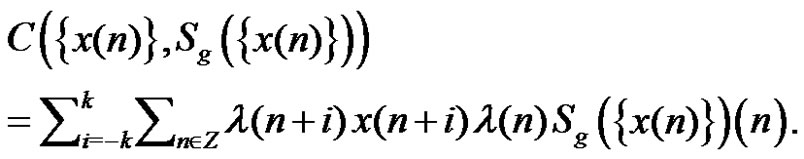
We call it the generalized correlativity of  and
and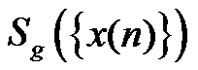 .
.
In particular, let 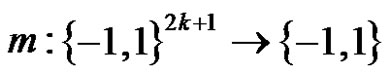 satisfy that for each
satisfy that for each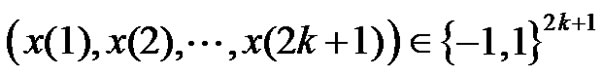 ,
,
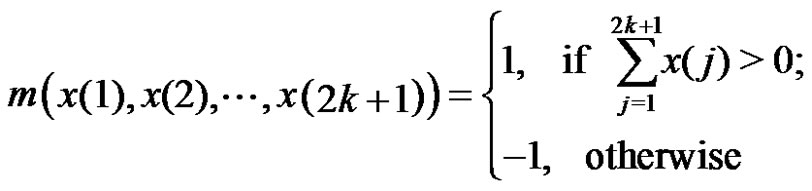
Then  is the median filtering operator and
is the median filtering operator and .
.
It is clear that the generalized correlativity is a measure of the relation between 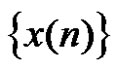 and
and . From a view of signal processing, it is shown that if we apply a stack filtering operator
. From a view of signal processing, it is shown that if we apply a stack filtering operator  to a signal
to a signal  with noise, then the generalized deviation
with noise, then the generalized deviation 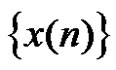 and
and  may be a measure of the
may be a measure of the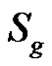 ’s capability of removing noise in the signal.
’s capability of removing noise in the signal.
3. Optimality of Median Filtering Operator
In the optimal design of filters, it is usual to select the optimal filter using MSE criterion or MAE criterion, for example, the optimal design of L-filters is based on MSE criterion. Both MSE criterion and MAE criterion mean that output signal is closest to input signal, which implies their high correlativity. Therefore, we have the following definition.
Definition 4. Suppose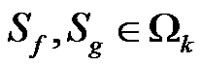 . If, for each
. If, for each  ,
,
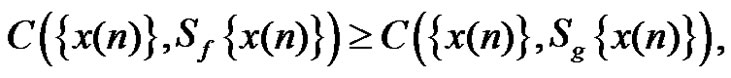
then we say that  is better than
is better than 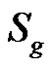 in terms of filtering behavior, denoted by “
in terms of filtering behavior, denoted by “ ”.
”.
Based on the definition, we have the following result.
Theorem 1. For any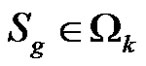 , we have
, we have 
Proof: Suppose that  and
and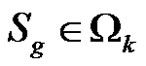 . Since
. Since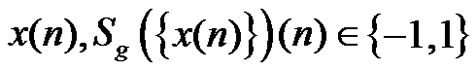 , we have
, we have

Now we prove that for each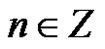 ,
,
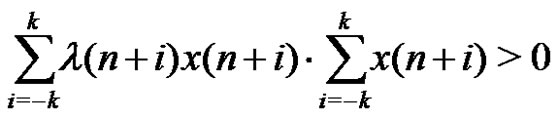 (1)
(1)
In fact, since 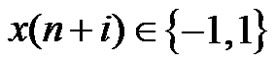 for i = –k, –k + 1
for i = –k, –k + 1 ,
,
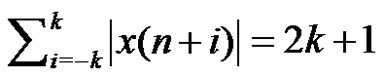 . Therefore,
. Therefore,
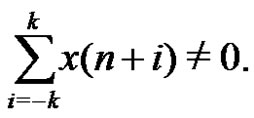
Case 1. 
In this case, we have
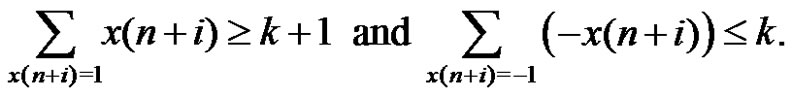
Thus

where


By the definition of sequence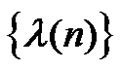 , for any
, for any 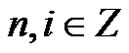 with
with , we have
, we have

and
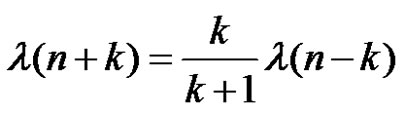 for
for 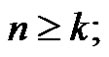

and
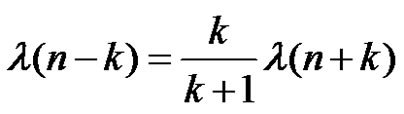 for
for 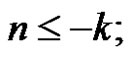
 for
for 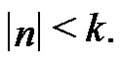
So we have
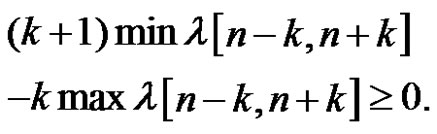 (2)
(2)
Thus
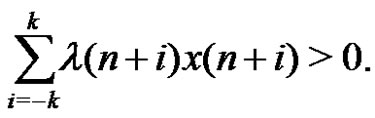
Therefore, (1) holds.
Case 2. 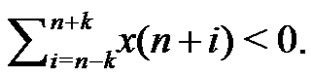
In this case, we have

Thus

By (2), we have
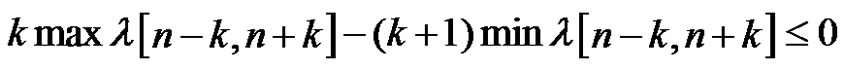
Thus

Therefore, (1) holds.
For any , if
, if , then
, then
 . By the definition of
. By the definition of ,
,
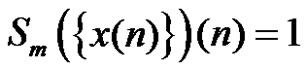 . Again
. Again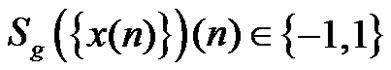 , so
, so
 . Therefore,
. Therefore,
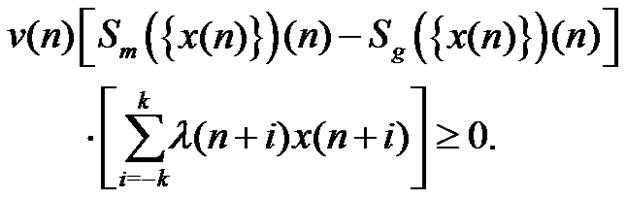
If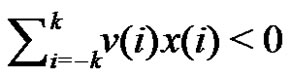 , then
, then . By the definition of
. By the definition of ,
, . Again
. Again , so
, so
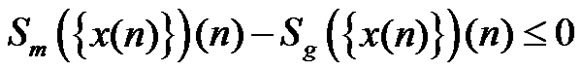 . Therefore,
. Therefore,
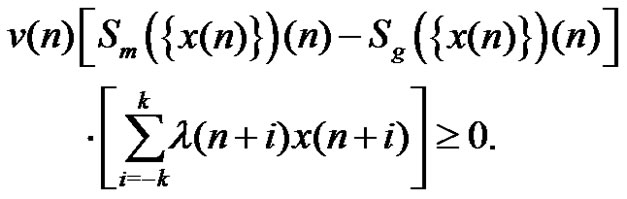
So

Therefore, for any 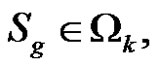

that is,

This completes the proof of Theorem 1.
This result shows that, in the sense of the generalized correlativity, the median filtering operator is optimal of the stack filtering operators. Also it is globally optimal, compared with the optimal design of L-filters.
4. Conclusion
In this paper we defined the generalized correlativity of input signal and output signal of a stack filtering operator, which can be used for numerously measuring these filtering operators’s behavior in removing noise in signals. In the sense of the criterion of the generalized correlativity, the median filtering operator is optimal of stack filtering operators, which implies that this filtering operator possesses better filtering behavior than the others.
REFERENCES
- J. W. Tukey, “Nonlinear (Nonsuperposable) Methods for Smoothing Data,” Proceedings of Congress Record EASCON, Washington DC, 7-9 October 1974, p. 673.
- H. X. Chen, R. K. Yang and M. Gabbouj, “On Root Structures and Convergence Properties of Weighted Median Filters,” Circuits and System Signal Processing, Vol. 14, No. 6, 1995, pp. 735-747. doi:10.1007/BF01204682
- U. Eckhardt, “Root Images of Median Filters,” Journal of Mathematical Imeging and Vision, Vol. 19, No. 1, 2003, pp. 63-70. doi:10.1023/A:1024489020930
- D. Eberly, H. Longbotham and J. Aragon, “Complete Classification of Roots to One-Demensional Median and Rank-Order Filters,” IEEE Transactions on Signal Processing, Vol. 39, No. 1, 1991, pp. 197-199. doi:10.1109/78.80781
- S. G. Tyan, “Median Filters: Deterinistic Properties,” In: Two-Dimension Digital Signal Processing II: Transforms and Median Filters, Springer, Berlin, 1981. doi:10.1007/BFb0057598
- P.-T. Yu and W.-L. Wang, “Root Properties of Median Filters under There Appending Strategies,” IEEE Transactions on Signal Processing, Vol. 41, No. 2, 1993, pp. 965-970. doi:10.1109/78.193236
- J. Brandt, “Cycles of Medians,” Utilitas Mathematica, Vol. 54, 1998, pp. 111-126.
- W. Z. Ye, L. Wang and L. G. Xu, “Properties of Locally Convergent Sequences with Respect to Median Filter,” Discrete Mathematics, Vol. 309, No. 9, 2009, pp. 2775- 2781. doi:10.1016/j.disc.2008.07.002
- W. Z. Ye, M. T. Zhang and Y. L. Ma, “Structure of Recurrent Sequences of Median Filters,” Discrete Mathematics, Vol. 310, No. 6-7, 2010, pp. 1253-1258. doi:10.1016/j.disc.2009.12.005
- Z.-J. Gan and M Mao, “Two Convergence Theorems on Deterministic Properties of Median Filters,” IEEE Transactions on Signal Processing, Vol. 39, No. 7, 1991, pp. 1689-1690. doi:10.1109/78.134410
- P. D. Wendt, E. J. Coyle and N. C. Gallagher Jr., “Stack Filter,” IEEE Transactions on Acoustics, Speech and Signal Processing, Vol. 34, No. 4, 1986, pp. 898-911. doi:10.1109/TASSP.1986.1164871
- W. Z. Ye and X. W. Zhou, “Criteria of Convergence of Median Filters,” IEEE Transactions on Signal Processing, Vol. 49, No. 2, 2001, pp. 360-363. doi:10.1109/78.902118
- T. A. Nodes and N. C. Gallagher, “The Output Distribution of Median-Type Filters,” IEEE Transactions on Communication, Vol. 32. No. 5, 1984, pp. 532-541. doi:10.1109/TCOM.1984.1096099
- A. C.Bovik, T. S. Huang and D. C. Munson, “A generalization of Median Filtering Using Linear Combinations of Order Statistics,” IEEE Transactions on Acoustics, Speech and Signal Processing, Vol. 31, No. 6, 1983, pp. 1342- 1349. doi:10.1109/TASSP.1983.1164247
- R. Oten and R. J. P. de Figueiredo, “An Efficient Method for L-Filter Design,” IEEE Transactions on Signal Processing, Vol. 51, No. 1, 2003, pp. 193-203. doi:10.1109/TSP.2002.806573
- J. P. Fitch, E. J. Coyle and N. C. Gallagher Jr., “Median Filtering by Threshold Decomposition,” IEEE Transactions on Acoustics, Speech and Signal Processing, Vol. 32, No. 6, 1984, pp. 1183-1188.
NOTES
*Supported by Shanghai Leading Academic Discipline Project (J50101), NSF of Shanghai (10ZR1412100), and NNSF of China (61071186).

