Open Journal of Discrete Mathematics
Vol.2 No.1(2012), Article ID:17152,4 pages DOI:10.4236/ojdm.2012.21001
Department of Mathematics, King Abdulaziz University, Jeddah, Saudi Arabia
Email: aalkenani10@hotmail.com
Received September 29, 2011; revised November 1, 2011; accepted November 12, 2011
Keywords: symmetric nets; codes
ABSTRACT
In this paper, we investigated the code over 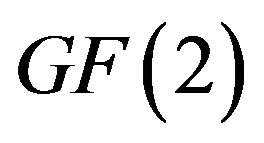 which is generated by the incidence matrix of the symmetric (2,4) - net
which is generated by the incidence matrix of the symmetric (2,4) - net . By computer search, we found that this binary code of
. By computer search, we found that this binary code of  has rank 13 and the minimum distance is 8.
has rank 13 and the minimum distance is 8.
1. Introduction
A 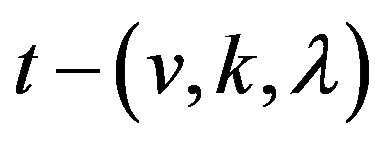 design
design  is an incidence structure with
is an incidence structure with 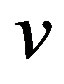 points,
points, 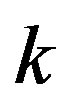 points on each block and any subset of
points on each block and any subset of 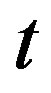 points is contained in exactly
points is contained in exactly  blocks, where
blocks, where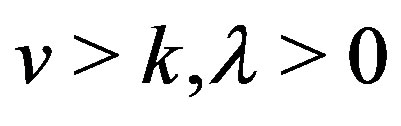 . the number of blocks is
. the number of blocks is 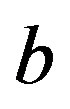 and the number of blocks on a point is
and the number of blocks on a point is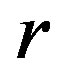 .
.
The design  is resolvable if its blocks can be partitioned into
is resolvable if its blocks can be partitioned into 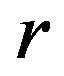 parallel classes, such that each parallel class partitions the point set of
parallel classes, such that each parallel class partitions the point set of . Blocks in the same parallel class are parallel. Clearly each parallel class has
. Blocks in the same parallel class are parallel. Clearly each parallel class has 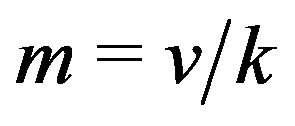 blocks.
blocks.  is affine resolvable, or simply affine, if it can be resolved so that any two nonparallel blocks meet in
is affine resolvable, or simply affine, if it can be resolved so that any two nonparallel blocks meet in 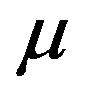 points, where
points, where 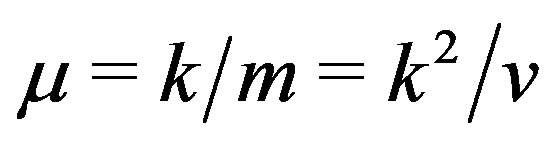 is constant. Affine 1-designs are also called nets. The dual design of a design
is constant. Affine 1-designs are also called nets. The dual design of a design  is denoted by
is denoted by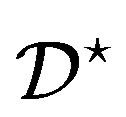 . If
. If  and
and 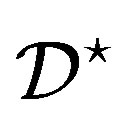 are both affine, we call
are both affine, we call  a symmetric net. We use the terminology of Jungnickel [1] (see also [2-5]). In this case
a symmetric net. We use the terminology of Jungnickel [1] (see also [2-5]). In this case 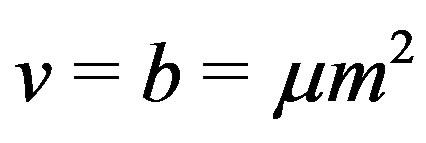 and
and 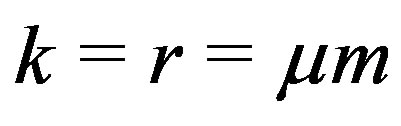 . That is,
. That is,  is an affine
is an affine 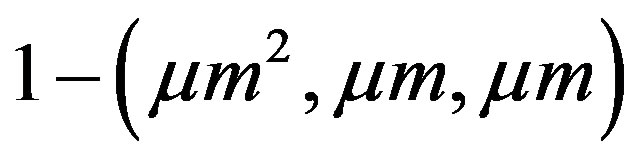 design whose dual
design whose dual 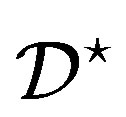 is also affine with the same parameters. For short we call such a symmetric net a
is also affine with the same parameters. For short we call such a symmetric net a 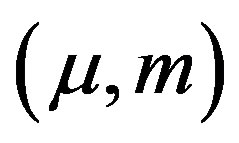 -net.
-net.
If  is a symmetric net we shall refer to the parallel classes of
is a symmetric net we shall refer to the parallel classes of  as block classes of
as block classes of  and to the parallel classes of
and to the parallel classes of 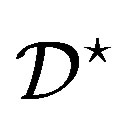 as point classes of
as point classes of .
.
For any finite structure  with point set
with point set  and block set
and block set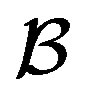 , the code
, the code 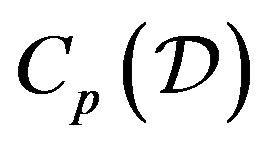 of
of  over prime field
over prime field 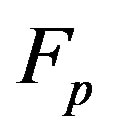 is the subspace of the space
is the subspace of the space 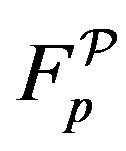 of all functions from
of all functions from 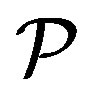 to
to 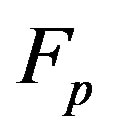 that is spanned by the incidence vectors of the blocks of
that is spanned by the incidence vectors of the blocks of . This code is equivalent to the code given by the column space of any incidence matrix of the incidence structure, where we use the blocks to index the columns (and the points the rows) of the incidence matrix.
. This code is equivalent to the code given by the column space of any incidence matrix of the incidence structure, where we use the blocks to index the columns (and the points the rows) of the incidence matrix.
2. The Symmetric Net with 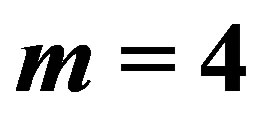 and
and 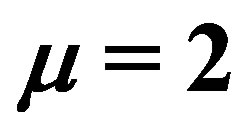
The symmetric net that we shall be concerned with in this paper is the one with 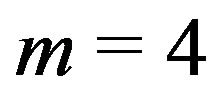 and
and 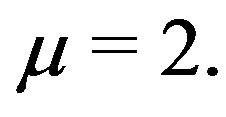 As a design it has parameters
As a design it has parameters
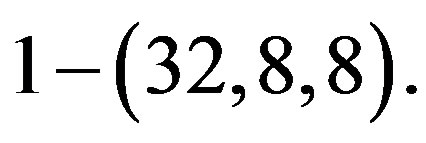
Its incidence matrix is (1).
A computer search has shown that to within isomorphism there is only one symmetric net with these parameters. We denote this symmetric net by .
.
Butson [6] showed that there exist symmetric nets with 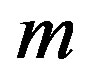 any prime and
any prime and 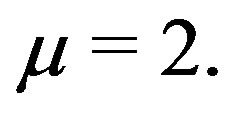 This was extended to
This was extended to  any prime power by Jungnickel [7]. Therefore
any prime power by Jungnickel [7]. Therefore  is one of the family of symmetric nets constructed by Jungnickel.
is one of the family of symmetric nets constructed by Jungnickel.
3. The Codes
The columns of the incidence matrix of  can be considered as vectors of the 32-dimensional vector space over any finite prime field
can be considered as vectors of the 32-dimensional vector space over any finite prime field 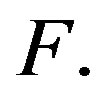 The subspace they generate is the code of the net
The subspace they generate is the code of the net  over
over 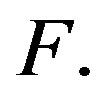 By computer we found that the binary code (that is, the code over the field of order 2) of
By computer we found that the binary code (that is, the code over the field of order 2) of  has rank 13. The weight distribution of its codewords is given below. The all one vector is in the code since it is obtained as the sum of the 4 columns corresponding to the blocks of any parallel class in the incidence matrix. Therefore the code is self-complementary in that the complement of a codeword is also a codeword, see [8] or [9]. Hence we only list the number of codewords of weight up to 16.
has rank 13. The weight distribution of its codewords is given below. The all one vector is in the code since it is obtained as the sum of the 4 columns corresponding to the blocks of any parallel class in the incidence matrix. Therefore the code is self-complementary in that the complement of a codeword is also a codeword, see [8] or [9]. Hence we only list the number of codewords of weight up to 16.

Since the minimum distance is 8, the binary code is 3-error correcting.
There doesn’t seem to be an easy proof that the dimension of the code is 13 over the binary field. The dimension of the code of  for odd characteristic is 25. This we prove in this paper.
for odd characteristic is 25. This we prove in this paper.
The incidence matrix of  may be put in the form:
may be put in the form:
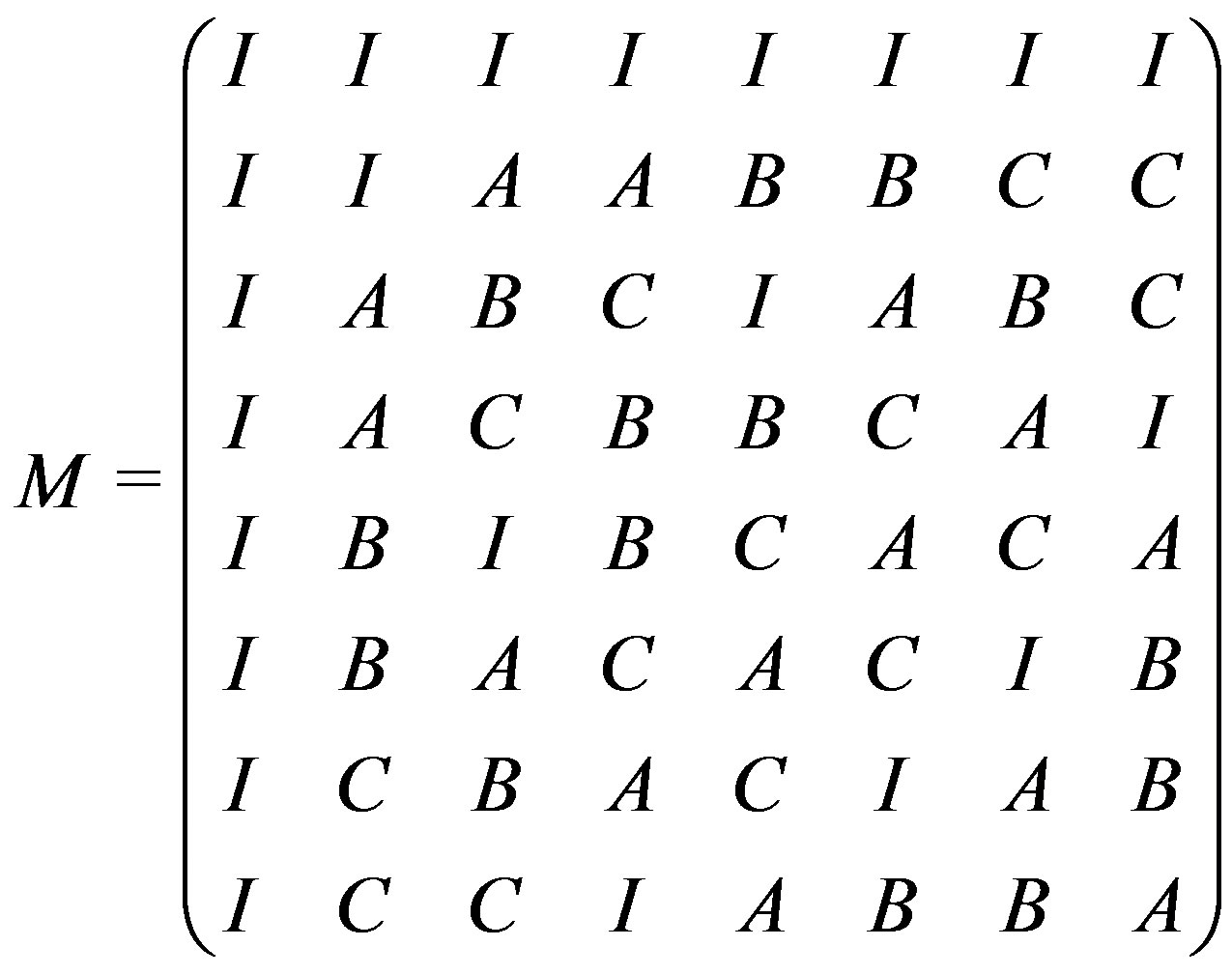
where
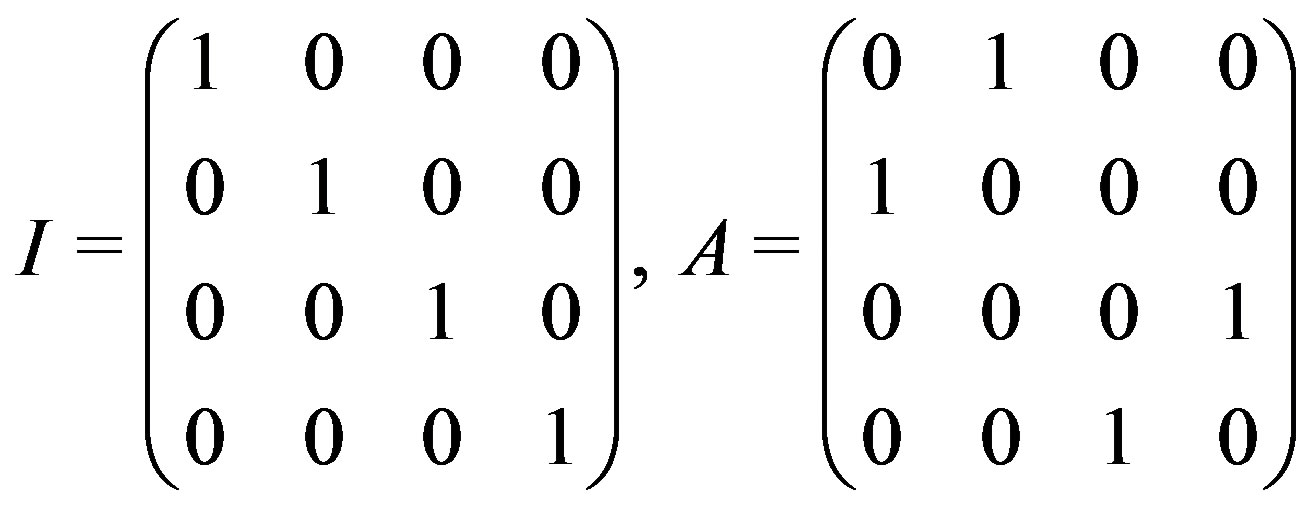
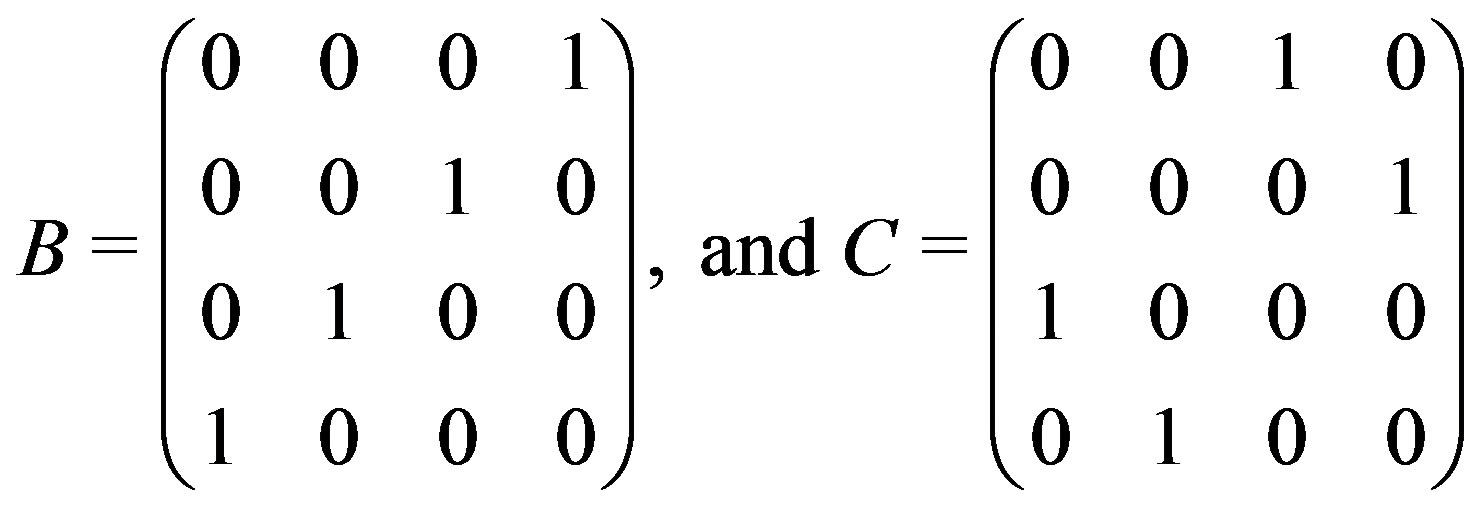
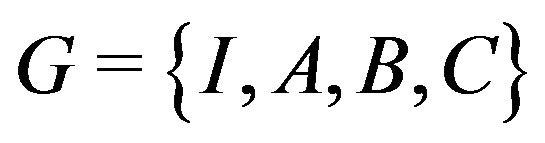 is an elementary abelian group of order 4.
is an elementary abelian group of order 4.
First suppose that the characteristic of the field is not 2.
The matrices in 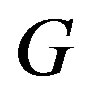 can be simultaneously diagonalised by
can be simultaneously diagonalised by
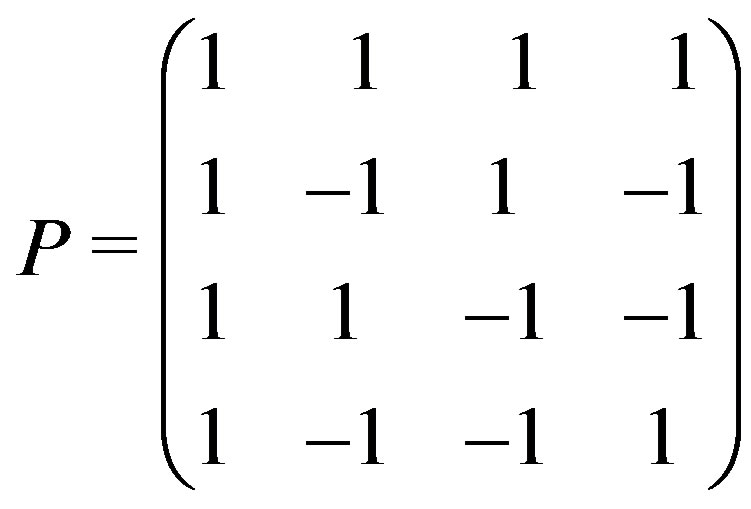
Conjugating by diagonal 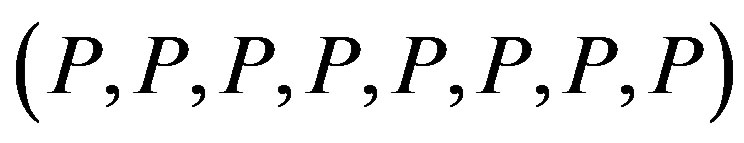 and then by
and then by , the permutation matrix which moves rows (and columns)
, the permutation matrix which moves rows (and columns) 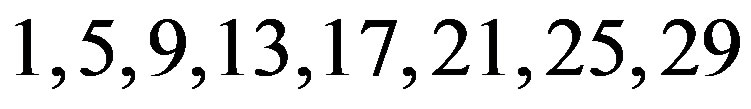 to the first eight positions, rows (and columns)
to the first eight positions, rows (and columns) 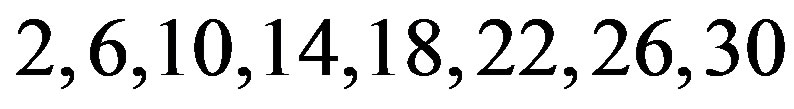 to the next eight positions, rows (and columns)
to the next eight positions, rows (and columns)  to the next eight positions, rows (and columns)
to the next eight positions, rows (and columns) 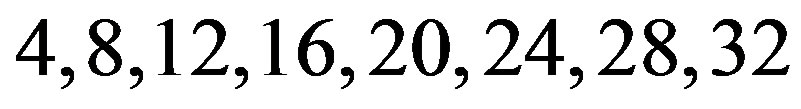 to the last eight positions, we get
to the last eight positions, we get 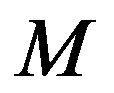 conjugate to
conjugate to

have determinant 4096. In fact they are Hadamard matrices. Hence the rank of 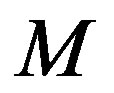 is
is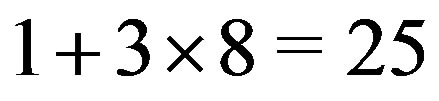 , if the characteristic is not 2.
, if the characteristic is not 2.
4. Acknowledgements
The author would like to thank the Deanship of Scientific Research at King Abdulaziz University for supporting a project no. 169/428, where this paper is a part of that project.
REFERENCES
- T. Beth, D. Jungnickel and H. Lenz, “Design Theory,” Cambridge University Press, Cambridge, 1999.
- C. J. Colbourn and J. H. Dinitz, “The CRC Handbook of Combinatorial Designs,” CRC Press, Boca Raton, New York, London, Tokyo, 1996.
- Y. J. Ionin and M. S. Shrikhande, “Combinatorics of Symmetric Designs,” Cambridge University Press, Cambridge, 2006.
- A. N. Al-Kenani and V. C. Mavron, “Non-Tactical Symmetric Nets,” Journal of the London Mathematical Society, Vol. 67, No. 2, 2003, pp. 273-288. doi:10.1112/S0024610702004052
- V. C. Mavron and V. D. Tonchev, “On Symmetric Nets and Generalised Hadamard Matrices from Affine Designs,” Journal of Geometry, Vol. 67, No. 1-2, 2000, pp. 180-187. doi:10.1007/BF01220309
- A. T. Butson, “Generalized Hadamard Matrices,” Proceedings of the American Mathematical Society, Vol. 13, 1962, pp. 894-898. doi:10.1090/S0002-9939-1962-0142557-0
- D. Jungnickel, “On Difference Matrices, Resolvable Transversal Designs and Generalised Hadamard Matrices,” Mathematische Zeitschrift, Vol. 167, No. 1, 1979, pp. 49-60. doi:10.1007/BF01215243
- E. F. Assmus Jr. and J. D. Key, “Designs and Their Codes,” Cambridge Tracts in Mathematics, Vol. 103, Cambridge University Press, 1992.
- V. D. Tonchev, “Quasi-Symmetric Designs, Codes, Quadrics, and Hyperplane Sections,” Geometriae Dedicata, Vol. 48, No. 3, 1993, pp. 295-308. doi:10.1007/BF01264073

