Open Journal of Discrete Mathematics
Vol.1 No.1(2011), Article ID:4575,5 pages DOI:10.4236/ojdm.2011.11001
Factoring Elementary p-Groups for p ≤ 7
Institute of Mathematics and Informatics, University of Pécs, Ifjúság, Pécs, Hungary
E-mail: sszabo7@hotmail.com
Received March 10, 2011; revised March 20, 2011; accepted April 5, 2011
Keywords: factorization of finite abelian groups, full-rank subset, full-rank factorization, periodic subset, periodic factorization, Rédei’s conjecture, Corrádi’s conjecture
Abstract
It is an open problem if an elementary p-group of rank k ≥ 3 does admit full-rank normalized factorization into two of its subsets such that one of the factors has p elements. The paper provides an answer in the p ≤ 7 special case.
1. Introduction
Let G be a finite abelian group. We use multiplicative notation in connection with abelian groups and e will denote the identity element of G. For two subset A and B of G the product AB is defined to be consisting of all the elements ab, where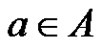 ,
,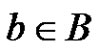 . If
. If
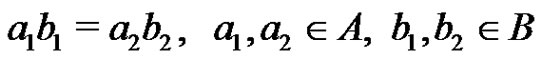
imply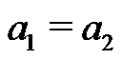 ,
, 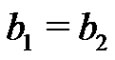 , then we say that the product AB is direct. If the product AB is direct and is equal to G, then the equation
, then we say that the product AB is direct. If the product AB is direct and is equal to G, then the equation 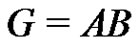 is called a factorization of G.
is called a factorization of G.
We say that a subset A of G is normalized if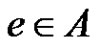 . The factorization
. The factorization 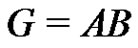 is called a normalized factorization if the factors A and B are normalized. A normalized subset A of G is termed a full-rank subset of G if
is called a normalized factorization if the factors A and B are normalized. A normalized subset A of G is termed a full-rank subset of G if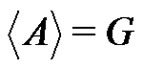 . Here
. Here 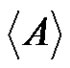 denotes the span of A in G. In other words
denotes the span of A in G. In other words 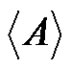 is the smallest subgroup of G containing A. A normalized factorization
is the smallest subgroup of G containing A. A normalized factorization 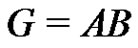 is called a full-rank factorization if the factors A and B are full-rank subsets of G.
is called a full-rank factorization if the factors A and B are full-rank subsets of G.
Let p be a prime and let k be a positive integer. A group that is a direct product of k cyclic groups of order p is called an elementary p-group of rank k. In 1970 in the open problems section in his book [4] L. Rédei advanced the following conjecture.
Conjecture 1 Let p be a prime. An elementary p-group of rank 3 does not admit any full-rank factorization.
Let 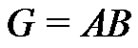 be a normalized factorization, where G is an elementary p-group of rank 3. One of the factors A and B must have p elements while the other factor must have
be a normalized factorization, where G is an elementary p-group of rank 3. One of the factors A and B must have p elements while the other factor must have 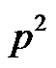 elements. A normalized subset of order p in the
elements. A normalized subset of order p in the 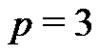 case cannot contain three generator elements of the group. Thus Rédei’s conjecture holds for
case cannot contain three generator elements of the group. Thus Rédei’s conjecture holds for 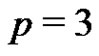 and for the remaining part we may restrict our attention to the
and for the remaining part we may restrict our attention to the 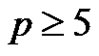 case.
case.
In 1998 S. Szabó and C. Ward [7] carried out a computer assisted exhaustive search to verify Rédei’s conjecture for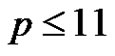 . In a private conversation K. Corrádi proposed the following generalization to Rédei’s conjecture.
. In a private conversation K. Corrádi proposed the following generalization to Rédei’s conjecture.
Conjecture 2 Let p be a prime and let G be an elementary p-group of rank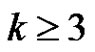 . If
. If 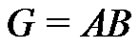 is a normalized factorization of G such that
is a normalized factorization of G such that 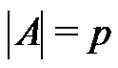 and
and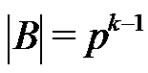 , then at least one of the factors does not span G.
, then at least one of the factors does not span G.
The normalized factor A can contain only 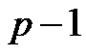 generator elements of G and so the generalized conjecture certainly holds for
generator elements of G and so the generalized conjecture certainly holds for 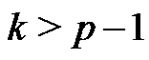 and so it is enough to deal with the
and so it is enough to deal with the 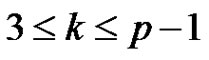 case.
case.
In this note we verify Corrádi's conjecture for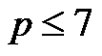 .
.
2. The k = 3 Case
At certain points in this paper we rely on some elementary concepts of graph theory. We presents these here. Let Γ be a simple graph, that is, Γ does not have double edges or loops. The set of vertices of Γ is denoted by V. Suppose U is a subset of V. If each two distinct elements of U are always connected in Γ by an edge of Γ, then the subgraph Δ of Γ spanned by U is called a clique of Γ. The set of vertices of Δ is U. If U has k elements, then we say that Δ is a clique of size k of Γ. Sometimes we express this fact simply by saying the Δ is a k-clique of Γ. The following problem is called the listing version of the k-clique problem.
Problem 1 Given a finite simple graph Γ and a positive integer k. List all k-cliques of Γ.
By the complexity theory of computation, Problem 1 belongs to the NP complete complexity class. Loosely speaking Problem 1 is computationally hard. We will solve two instances of the k-clique problem. In these cases the sizes of Γ are not overly large and the existing algorithms presented in [1,3] can handle them.
Let p be a prime and let G be an elementary p-group of rank 3 with basis elements x1, x2, x3, where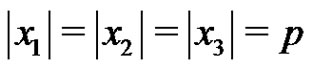 . Let
. Let 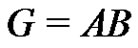 be a normalized factorization of G such that
be a normalized factorization of G such that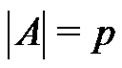 ,
,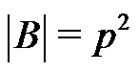 .
.
Proposition 1 For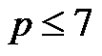 ,
, 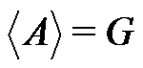 implies that B is a subgroup of G.
implies that B is a subgroup of G.
Proof. As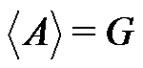 , we may choose the basis elements x1, x2, x3 such that
, we may choose the basis elements x1, x2, x3 such that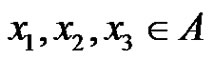 . We will work with the subset
. We will work with the subset 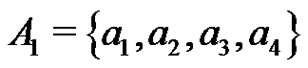 of A, where
of A, where
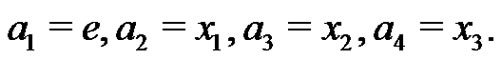
For each i, j, 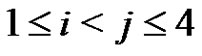 we set
we set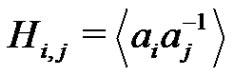 . Choose an
. Choose an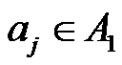 . Multiplying the factorization
. Multiplying the factorization 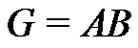 by
by 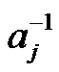 gives the normalized factorization
gives the normalized factorization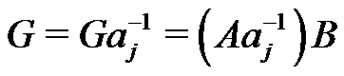 . By Lemma 5 of [2], in the factorization
. By Lemma 5 of [2], in the factorization 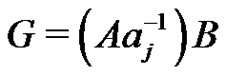 the factor
the factor 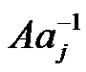 can be replaced by
can be replaced by 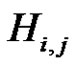 to get the normalized factorization
to get the normalized factorization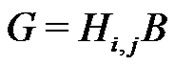 . Since the product
. Since the product 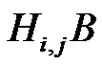 is direct, by Lemma 2.1 of [6],
is direct, by Lemma 2.1 of [6],
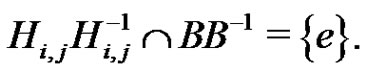
Plainly,  and so
and so
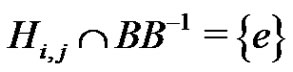
holds for each i, j,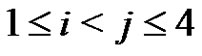 . Set
. Set
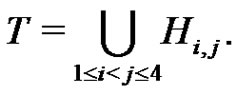
Clearly,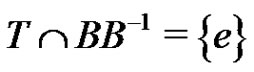 . We define a graph Γ. The nodes of Γ are the elements of G. Two nodes
. We define a graph Γ. The nodes of Γ are the elements of G. Two nodes 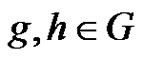 are connected if
are connected if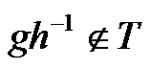 . We may call T a test set since we use it for testing if a pair
. We may call T a test set since we use it for testing if a pair 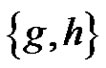 is an edge of Γ.
is an edge of Γ.
The graph Γ has 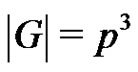 nodes. We focus our attention on cliques of size p2 in Γ. The reason is the following. If the products
nodes. We focus our attention on cliques of size p2 in Γ. The reason is the following. If the products 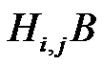 are direct for each i, j,
are direct for each i, j, 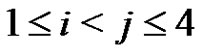 , then
, then 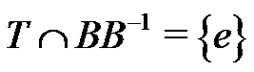 and so the elements of B form the nodes of a clique of size p2 in Γ. Conversely, if the elements of B are the nodes of a clique of size p2 in Γ, then
and so the elements of B form the nodes of a clique of size p2 in Γ. Conversely, if the elements of B are the nodes of a clique of size p2 in Γ, then 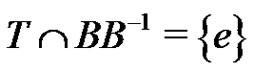 and hence the products
and hence the products 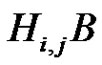 are direct for each i, j,
are direct for each i, j,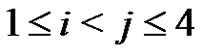 .
.
We call a clique normalized if e is one of its nodes. A computer assisted inspection reveals that each normalized cliques of size p2 in Γ is a subgroup of G.
One can draw the following conclusion. If 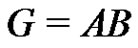 is a normalized factorization of G, where
is a normalized factorization of G, where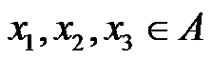 , then B must be a subgroup of G.
, then B must be a subgroup of G.
This completes the proof.
For p = 5 the graph Γ has 53 = 125 nodes. The search found 30 cliques of size 52 = 25. Each of them was a coset modulo some subgroup of order 25 of G. (The subgroup that plays the role of the modulus of course may vary from case to case.) In particular the normalized cliques of size 25 in Γ correspond to subgroups of G.
For p = 7 the graph Γ has 73 = 343 nodes. The inspection gave 140 cliques of size 72 = 49. Each of them turned out to be a coset modulo some subgroup of order 49.
For p = 11 the graph Γ does contain normalized cliques of size 112 that are not subgroups of G. So our approach to verify Rédei’s conjecture (or Corrádi’s conjecture) breaks down for 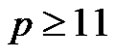 .
.
The above mentioned computer searches are not particularly demanding in terms of the time of computation. However, one cannot be cautious enough in connection with computer aided proofs. Therefore, in order to be on the safe side we used the algorithms described in [1,3] respectively as these algorithms have well tested implementations.
One can view the elements of G as points of the 3-dimensional affine space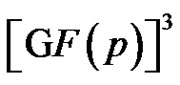 . Using geometrical terminology one can say that for
. Using geometrical terminology one can say that for 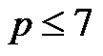 a clique of size p2 in Γ is a 2-dimensional linear complex in
a clique of size p2 in Γ is a 2-dimensional linear complex in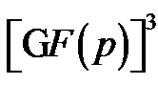 . A 2-dimensional linear complex is a translated copy of some 2-dimensional subspace of
. A 2-dimensional linear complex is a translated copy of some 2-dimensional subspace of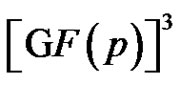 .
.
3. The k = 4 Case
Let p be a prime and let G be an elementary p-group of rank 4 with basis elements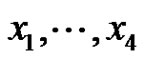 , where
, where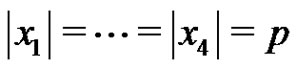 . Let
. Let 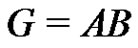 be a normalized factorization of G such that
be a normalized factorization of G such that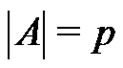 ,
,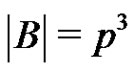 .
.
Proposition 2 For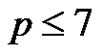 ,
, 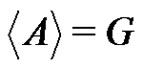 implies that B is a subgroup of G.
implies that B is a subgroup of G.
Proof. We may assume that 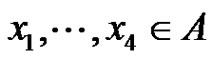 since this is only a matter of choosing the basis elements
since this is only a matter of choosing the basis elements 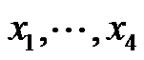 suitably. We set
suitably. We set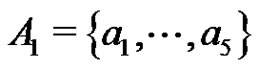 , where
, where
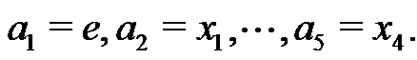
We know that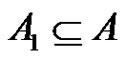 . For each i, j,
. For each i, j, 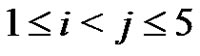 we set
we set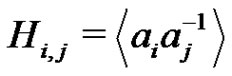 . By Lemma 5 of [2], in the factorization
. By Lemma 5 of [2], in the factorization 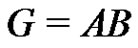 the factor A can be replaced by
the factor A can be replaced by 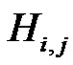 to get the normalized factorization
to get the normalized factorization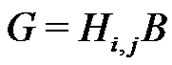 . As the product
. As the product 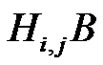 is direct, by Lemma 2.1 of [6], it follows that
is direct, by Lemma 2.1 of [6], it follows that
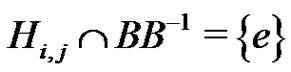 (1)
(1)
for each i, j,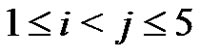 .
.
We partition B into subsets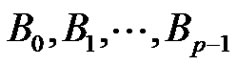 . Each
. Each 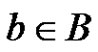 can be represented uniquely in the form
can be represented uniquely in the form
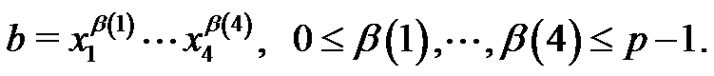 (2)
(2)
The set 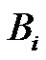 consists of each
consists of each 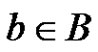 for which
for which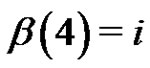 . Note that
. Note that
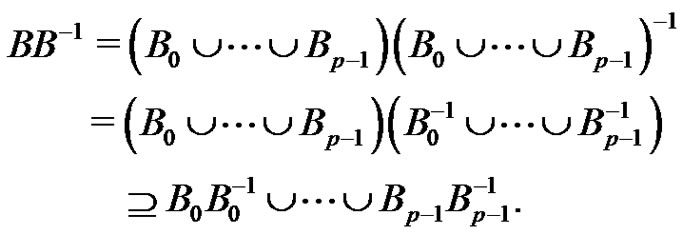
In particular it follows that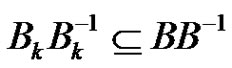 . We use now equations (1) only for i, j,
. We use now equations (1) only for i, j, 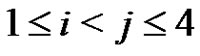 to conclude that
to conclude that
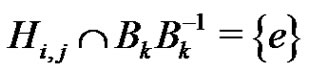 (3)
(3)
holds for each i, j, k, 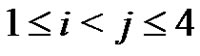 ,
,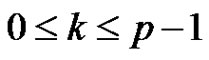 .
.
Set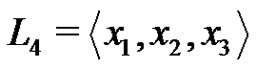 . (The index 4 intends to indicate that x4 is missing from the basis
. (The index 4 intends to indicate that x4 is missing from the basis 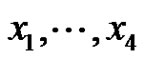 in the definition of
in the definition of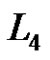 .) Set
.) Set
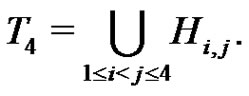
Obviously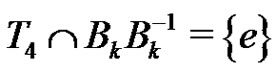 . We define a graph
. We define a graph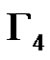 . The nodes of
. The nodes of 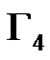 are the elements of
are the elements of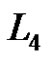 . Two nodes
. Two nodes 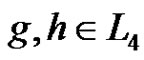 are connected if
are connected if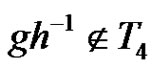 .
.
The graph 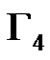 has
has 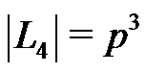 nodes. In addition
nodes. In addition 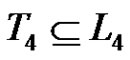 and
and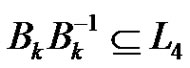 . Note that
. Note that 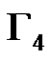 is isomorphic to the graph Γ used in the proof of Proposition 1. Consequently the nodes of a clique of size p2 in
is isomorphic to the graph Γ used in the proof of Proposition 1. Consequently the nodes of a clique of size p2 in 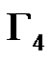 form a 2-dimensional linear complex in
form a 2-dimensional linear complex in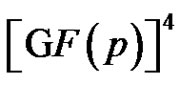 .
.
From (3) one can see that 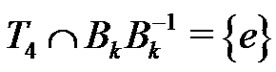 and consequently the elements of
and consequently the elements of 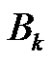 form the nodes of a clique of size p2 in
form the nodes of a clique of size p2 in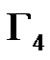 . Using geometrical terminology one may say that
. Using geometrical terminology one may say that 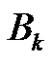 is a 2-dimensional linear complex in
is a 2-dimensional linear complex in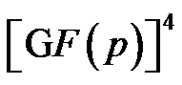 .
.
We set out now to prove that the union of the p disjoint 2-dimensional linear complexes 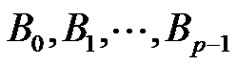 forms a 3-dimensional linear complex. This will show that B is in fact a subgroup of G of order p3.
forms a 3-dimensional linear complex. This will show that B is in fact a subgroup of G of order p3.
We partition B into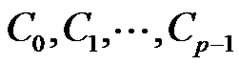 . Each
. Each 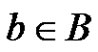 can be represented uniquely in the form (9). The set
can be represented uniquely in the form (9). The set 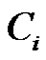 contains each
contains each 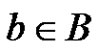 for which
for which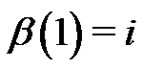 . Note that
. Note that
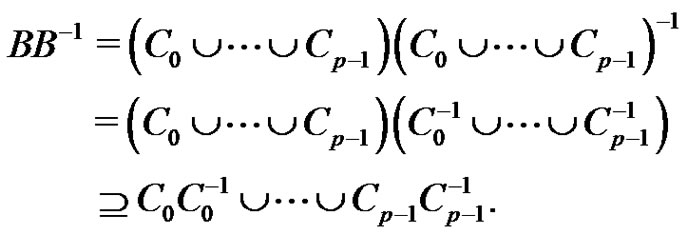
Therefore in particular 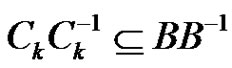 holds. We use now equations (1) only for i, j,
holds. We use now equations (1) only for i, j, 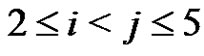 to conclude that
to conclude that
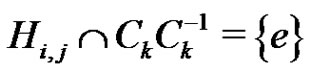 (4)
(4)
holds for each i, j, k, 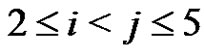 ,
,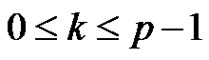 .
.
Set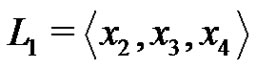 . (The meaning of the index 1 is that x1 is missing from the basis
. (The meaning of the index 1 is that x1 is missing from the basis 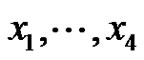 in the definition of the subgroup
in the definition of the subgroup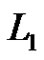 .) Set
.) Set
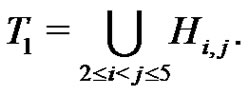
Plainly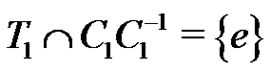 . We define a graph
. We define a graph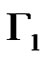 . The nodes of
. The nodes of 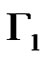 are the elements of
are the elements of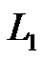 . Two nodes
. Two nodes 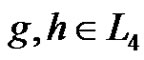 are connected if
are connected if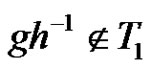 .
.
The graph 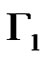 has
has 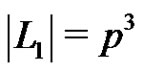 nodes. In addition
nodes. In addition 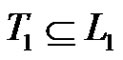 and
and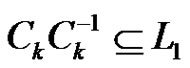 . Therefore, in fact
. Therefore, in fact 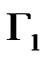 is isomorphic to the graph Γ we defined in the proof of Proposition 1. From (4) it follows that
is isomorphic to the graph Γ we defined in the proof of Proposition 1. From (4) it follows that 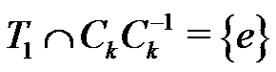 and so
and so 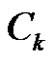 is a 2-dimensional linear complex in
is a 2-dimensional linear complex in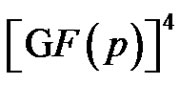 .
.
Let us observe that 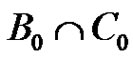 is a subgroup of G of order p. Using geometrical terminology
is a subgroup of G of order p. Using geometrical terminology 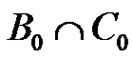 is a 1-dimensional linear complex in
is a 1-dimensional linear complex in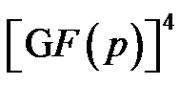 . We may view
. We may view 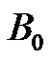 as a union of p disjoint 1-dimensional linear complexes. Similarly, we may view
as a union of p disjoint 1-dimensional linear complexes. Similarly, we may view 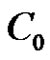 as a union of p disjoint 1-dimensional complexes. In addition each of these linear complexes is a translated copy of
as a union of p disjoint 1-dimensional complexes. In addition each of these linear complexes is a translated copy of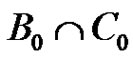 . Using the 1-dimensional linear complexes
. Using the 1-dimensional linear complexes
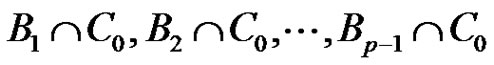
analogously we can conclude that B is a union of p2 disjoint 1-dimensional complexes each of which is a translated copy of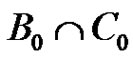 . The translation vectors form a 2-dimensional linear complex. Therefore B is a 3-dimensional linear complex in
. The translation vectors form a 2-dimensional linear complex. Therefore B is a 3-dimensional linear complex in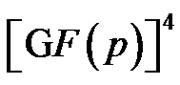 .
.
This completes the proof.
For the k = 6 case we need a corollary of Proposition 2. Set
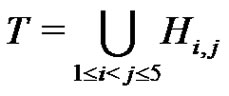
and define a graph Γ. The nodes of Γ are the elements of G. Two nodes 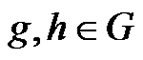 are connected if
are connected if .
.
Corollary 1 Each clique of size p3 in Γ corresponds to a 3-dimensional linear complex in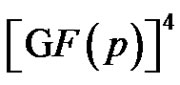 .
.
4. The k ≥ 5 Case
Let p be a prime and let G be an elementary p -group of rank 5 with basis elements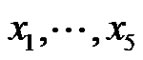 , where
, where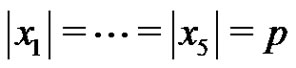 . Let
. Let 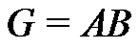 be a normalized factorization of G such that
be a normalized factorization of G such that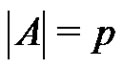 ,
,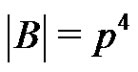 .
.
Proposition 3 For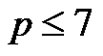 ,
, 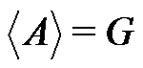 implies that B is a subgroup of G.
implies that B is a subgroup of G.
Proof. The proof is similar to the proof of Proposition 2 and we just outline the argument. It may be assumed that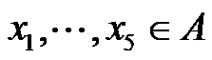 . We set
. We set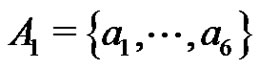 , where
, where
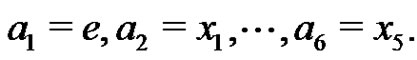
Clearly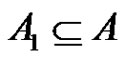 . For each i, j,
. For each i, j, 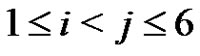 we set
we set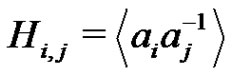 . From the factorization
. From the factorization 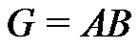 we get the normalized factorization
we get the normalized factorization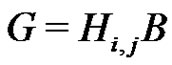 . From the directness of the product
. From the directness of the product 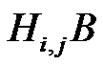 it follows that
it follows that
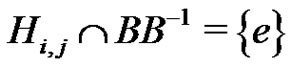 (5)
(5)
for each i, j,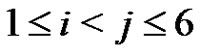 .
.
We partition B into subsets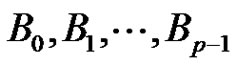 , Each
, Each 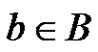 can be represented uniquely in terms of the basis
can be represented uniquely in terms of the basis 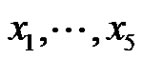 in the form
in the form
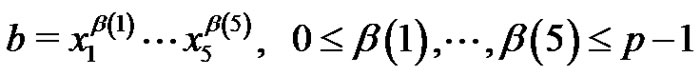 (6)
(6)
The set 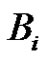 consists of each
consists of each 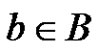 for which
for which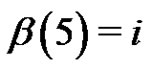 . It follows that
. It follows that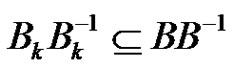 . The equations (5) for i, j,
. The equations (5) for i, j, 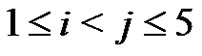 give that
give that
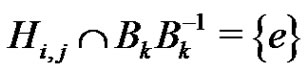 (7)
(7)
for each i, j, k, 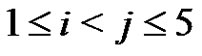 ,
,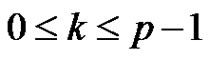 .
.
Set 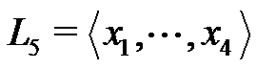 and
and
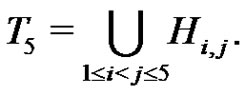
We define a graph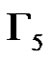 . The nodes of
. The nodes of 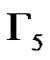 are the elements of
are the elements of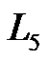 . Two nodes
. Two nodes 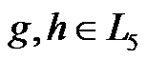 are connected if
are connected if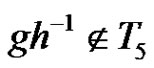 . Note that
. Note that 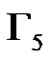 is isomorphic to the graph Γ in Corollary 1. From (7) one can see that the elements of
is isomorphic to the graph Γ in Corollary 1. From (7) one can see that the elements of 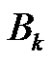 form the nodes of a clique of size p3 in
form the nodes of a clique of size p3 in 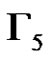 and so
and so
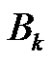 is a 3-dimensional linear complex in
is a 3-dimensional linear complex in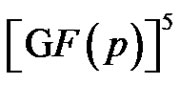 .
.
Next we partition B into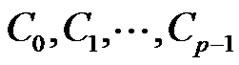 , where
, where 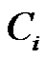 contains each
contains each 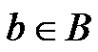 for which
for which 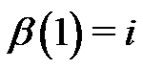 in the representation (6). A routine computation shows that
in the representation (6). A routine computation shows that 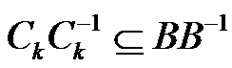 The equations (5) for i, j,
The equations (5) for i, j, 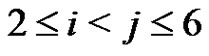 imply that
imply that
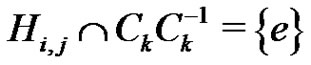 (8)
(8)
for each i, j, k, 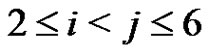 ,
,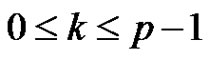 .
.
Set 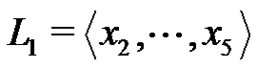 and
and
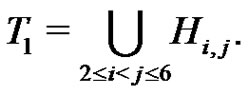
We define a graph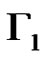 . The nodes of
. The nodes of 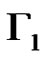 are the elements of
are the elements of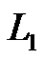 . Two nodes
. Two nodes 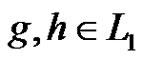 are connected if
are connected if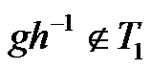 . Let us observe that
. Let us observe that 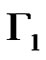 is isomorphic to the graph Γ in Corollary 1. From (8) it follows that
is isomorphic to the graph Γ in Corollary 1. From (8) it follows that 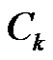 is a 3-dimensional linear complex in
is a 3-dimensional linear complex in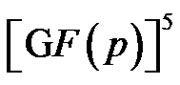 .
.
Using the fact that 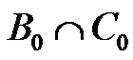 is a subgroup of G of order p2 one can show that B is a 4-dimensional linear complex in
is a subgroup of G of order p2 one can show that B is a 4-dimensional linear complex in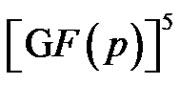 .
.
This completes the proof.
For the k = 6 case we need a corollary of Proposition 3. Set
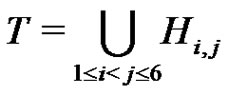
and define a graph Γ. The nodes of Γ are the elements of G. Two nodes 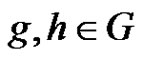 are connected if
are connected if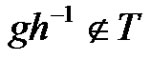 .
.
Corollary 2 Each clique of size p4 in Γ corresponds to a 4-dimensional linear complex in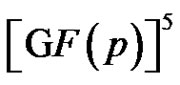 .
.
Let p be a prime and let G be an elementary p-group of rank 6 with basis elements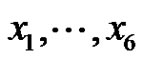 , where
, where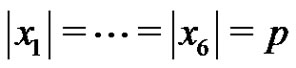 . Let
. Let 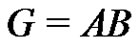 be a normalized factorization of G such that
be a normalized factorization of G such that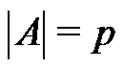 ,
,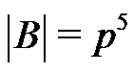 .
.
Proposition 4 For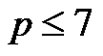 ,
, 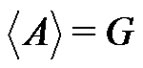 implies that B is a subgroup of G.
implies that B is a subgroup of G.
Proof. The proof is similar to the proof of Proposition 3 and we do not detail it.
We spell out the main result of this note formally as a theorem.
Theorem 1 Let G be a finite elementary p-group, where p is a prime and let 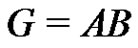 be a normalized factorization such that
be a normalized factorization such that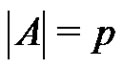 . If
. If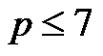 , then either
, then either 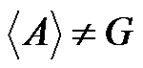 or
or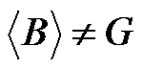 .
.
5. An Application
Let G be a finite abelian group and let A be a subset of G. We say that the subset A is periodic if there is an element 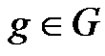 such that
such that 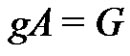 and
and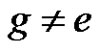 . A factorization
. A factorization 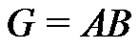 is called periodic if the factors A and B are both periodic. A. D. Sands has proved the following lemma. (See Lemma 3 of [5].)
is called periodic if the factors A and B are both periodic. A. D. Sands has proved the following lemma. (See Lemma 3 of [5].)
Lemma 1 Let 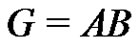 be a factorization of a finite abelian group G such that
be a factorization of a finite abelian group G such that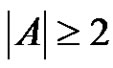 ,
,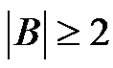 . If
. If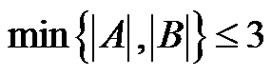 , then the factorization
, then the factorization 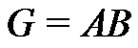 is periodic.
is periodic.
Motivated by this result we prove the next theorem.
Theorem 2 Let 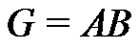 be a normalized factorization of a finite abelian group G such that
be a normalized factorization of a finite abelian group G such that 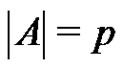 is a prime and
is a prime and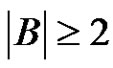 . If
. If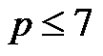 , then either
, then either 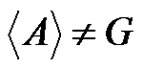 or B is periodic.
or B is periodic.
Proof. Let 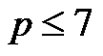 be a prime and consider a normalized factorization
be a prime and consider a normalized factorization 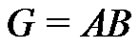 of a finite abelian group G such that
of a finite abelian group G such that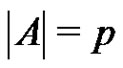 ,
, 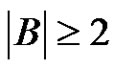 and
and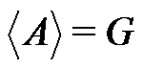 . We claim that B is periodic.
. We claim that B is periodic.
If 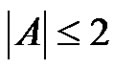 or
or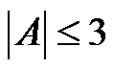 , then by Sands’ lemma it follows that either A or B is periodic. Thus for the remaining part of the proof we may assume that
, then by Sands’ lemma it follows that either A or B is periodic. Thus for the remaining part of the proof we may assume that 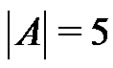 or
or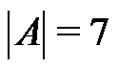 .
.
Choose an element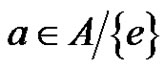 . By Lemma 5 of [2], in the factorization
. By Lemma 5 of [2], in the factorization 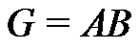 the factor A can be replaced by
the factor A can be replaced by 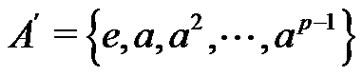 to get the normalized factorization
to get the normalized factorization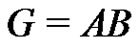 . This factorization is equivalent to the fact that the sets
. This factorization is equivalent to the fact that the sets
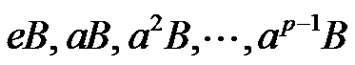 (9)
(9)
form a partition of G. Multiplying the factorization 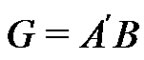 by the element a we get the normalized factorization
by the element a we get the normalized factorization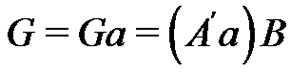 . This factorization is equivalent to the fact that the sets
. This factorization is equivalent to the fact that the sets
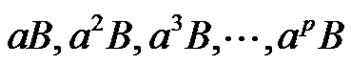 (10)
(10)
form a partition of G. Comparing the partitions (9) and (10) provides that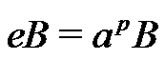 . Therefore, if
. Therefore, if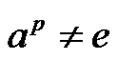 , then B is periodic. Thus for the remaining part of the proof we may assume that
, then B is periodic. Thus for the remaining part of the proof we may assume that 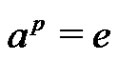 for each
for each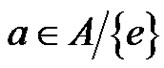 . As
. As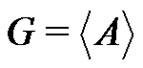 , it follows that G is an elementary p-group. From the factorization
, it follows that G is an elementary p-group. From the factorization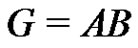 , by Theorem 1, it follows that either
, by Theorem 1, it follows that either 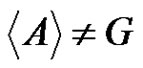 or
or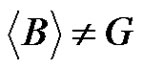 . Using
. Using 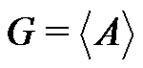 we get that
we get that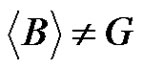 .
.
The reader can check that in the course of the proof of Theorem 1 we obtained the following side result. Let G be a finite elementary p-group where 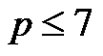 is a prime. If
is a prime. If 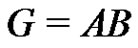 is a normalized factorization such that
is a normalized factorization such that 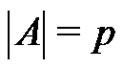 and
and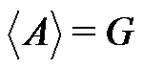 , then B is a subgroup of G. Clearly, a subgroup B of G is a periodic subset unless
, then B is a subgroup of G. Clearly, a subgroup B of G is a periodic subset unless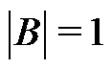 . But in our case, by the hypotheses of the theorem,
. But in our case, by the hypotheses of the theorem, 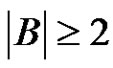 holds.
holds.
This completes the proof.
6. References
[1] R. Carraghan and P. M. Pardalos, “An exact algorithm for the maximum clique problem,” Operation Research Letters 9 (1990), 375-382. doi:10.1016/0167-6377(90)90057-C
[2] K. Corrádi, S. Szabó and P. Hermann, “A character free proof for Rédei's theorem,” Mathematica Pannonica 20 (2009), 3-15.
[3] P. R. J. Östergå rd, “A fast algorithm for the maximum clique problem,” Discrete Applied Mathematics 120 (2002), 195-205.
[4] L. Rédei, Lückenhafte Polynome über endlichen Körpern, Birkhäuser Verlag, Basel 1970, (English translation: Lacunary Polynomials over Finite Fields, North-Holland, Amsterdam, 1973.)
[5] A. D. Sands, “On the factorisation of finite abelian groups,” Acta Math. Acad. Sci. Hung. 8 (1957), 65-86. doi:10.1007/BF02025232
[6] S. Szabó and A. D. Sands, “Factoring Groups into Subsets,” CRC Press, Taylor and Francis Group, Boca Raton, 2009.
[7] S. Szabó and C. Ward, “Factoring elementary groups of prime cube order into subsets,” Mathematics of Computation 67 (1998), 1199-1206. doi:10.1090/S0025-5718-98-00929-6

