Received 14 September 2015; accepted 8 November 2015; published 11 November 2015

ABSTRACT

An optical encryption of three-dimensional (3D) object with digital holography was implemented. In the process of encryption, two holograms involved recording key information and 3D object were obtained. In the process of decryption, the 3D object was reconstructed from the two holograms by extracting the object and key information, followed by multiplication of the two holograms and inverse Fresnel transform numerically. The robustness of the method was also tested for different occlusions attacks and Gaussian noises. The results showed that the method was able to encrypt and decrypt the 3D object while being robust under different occlusions attacks and Gaussian noises.

Keywords:

Optical Encryption, Three-Dimensional Object, Digital Holography, Fresnel Diffraction

1. Introduction

Optical encryption is applied in numerous engineering fields for its competitive efficiency, parallel processing capability, and superior information storage capacity [1] -[8] . Mostly, numerical simulation methods have been applied due to the difficulties involved in the precise control of the optical devices alignment requirement. For addressing the problem of optical devices alignment required by the decryption process, less-alignment needed optical devices have been applied in previous research [9] [10] . For example, the joint transform correlator method was utilized for this, where photorefractive was used to record optical information. Though optical device alignment problem was partially addressed, the information storage and transmission was inconvenient with this method.

Optical digital holographic encryption technique was developed and popularized recently owning to its advantages of conveniences of data recording, transmission, and processing [11] - [14] . Various optical digital holographic encryption methods have been in use such as two, three, or four steps phase shift interference methods [15] - [18] . A disadvantage of these methods, however, is that the accuracy of phase shift is difficult to control. Additionally, most of the studies on encryption only involved encrypting two-dimensional image, though encryption of three dimensional (3D) object technique was also available, which utilized complex phase shift interference techniques [19] [20] .

In this research, an encryption of tangible 3D object was proposed. In this new method, two separate off-axis Fresnel holograms were recorded. The first hologram involved recording the 3D object and encryption key, and the second hologram only recorded encryption key. Following the hologram recording, encrypted information of 3D object and encryption key was extracted by the filtering out of zeroth-order information and conjugate information in frequency domain. Similarly, for second hologram, encrypted information of encryption key was extracted through filtering out of zeroth-order information and conjugate information in frequency domain. Multiplication of the first and the conjugate of second extracted information was performed, which followed by inverse Fourier transform to get the 3D object wave on the hologram plane. The Fresnel transform was then used for reconstructing decrypted images in the object domain. Furthermore, the decrypted images with different diffractive distances were also obtained. For reducing the effects of speckle noises on reconstructed images, a speckle noise suppression method was applied by averaging multiple reconstructed images. The robustness of the method was tested against occlusion and noise attacks.

2. Method

2.1. Encryption Process

The encryption process contains two optical paths. The first optical path is used to record a digital hologram I_E with 3D object and encryption keys of two random phase masks shown in Figure 1. The He-Ne light is divided into two light beams by BS₁. One beam passes through the random phase mask (RPM₂), acting as a reference

wave, which is placed on the front focal plane of lens L₄. The combination of lens L₃ and L₄ with same focus length consists of a 4f optical system. The other beam illuminates the 3D object after being reflected by M₃. The reflected wave from the 3D object, acting as a object wave, passes through the random phase mask (RPM₁) which is placed on the front focal plane of lens L₁. The combination of L₁ and L₂ is also a 4f system. The hologram I_E, which is thus an interference pattern formed by the reference wave and the object wave superim-

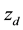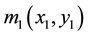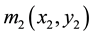position. The object can be treated as a two-dimensional image at different distances to the RPM₁ [19] . Let and denote the RPM₁ and RPM₂, respectively. The hologram I_E captured by CCD can be written in below:

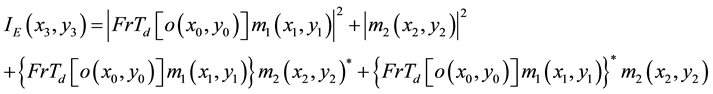(1)

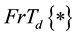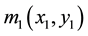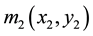where denotes Fresnel transform. d is diffraction distance. denotes a two-dimensional images at specific distance relative to the RPM₁ [19] . and denote the RPM₁ and RPM₂.

The second optical path is to record a digital hologram of the encryption key I_M shown in Figure 2. The hologram, an interference pattern formed by the superimposition of the reference wave which passes through RPM₂ and the object wave passing through RPM₁. This hologram contains the information of encryption key, which can be expressed with:

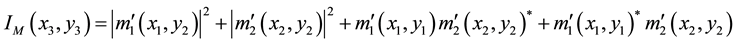(2)

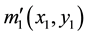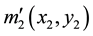where and denote the RPM₁ and RPM₂.

2.2. Decryption Process

In order to extract the encrypted information of 3D object and encryption key, zeroth, first order and conjugate of the hologram in frequency domain have to be separated. As such, the reference beam was slightly inclined planar wave for the separation of them. Following the separation, the two recorded holograms were Fourier transformed to extract the third term on the right hand side of Equation (1) and the fourth term on the right-hand side of Equation (2) [21] . Then the extracting spectrum was inverse Fourier transformed and the extracted items were multiplied. The encrypted 3D object information can be extracted by propagating a distance with Fresnel transformation, which can be expressed as:

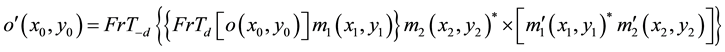(3)

When the 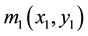is the same as and is the same as, the is the a scaled version of through Equation (4):

(4)

3. Experimental Setup

The experimental system is shown in Figure 3. It is based on Mach-Zehnder interferometer architecture. A He-Ne laser was used as a coherent light source. BS is a beam splitter, M is mirror and L is lens. The focal length of L₁ and L₂ is 30 cm and the focal length of L₃ and L₄ is 40 cm. RPM is random phase mask, which was made from glass corroded by hydrofluoric acid. The 3D object is located at an approximate distance d from the RPM₁ in the object wave.

In the experiments, the encrypted target object consists of two dices. The size of the dice in this experiment is 5 mm × 5 mm × 5 mm, with distance between them is 70 mm. A CCD (4M180MCL) camera which recorded hologram with resolution of 2048 × 2048, pixel size of is made in Canada IO industries Inc. The distance between front dice and the CCD is about 1680 mm. The reference beam is a slightly inclined planar and the angle between the reference beam and the object beam is 2 degrees.

4. Secondary Data Reduction and Analysis

The reconstructed image quality was degraded by speckle noise [22] . In order to reduce the effects of noise, a number of independently captured holograms were used for reducing the noise. Following the superposition of these independently captured holograms, it is estimated that the speckle noise of the hologram can be reduced to [22] :

(5)

where M is the number of independently captured holograms.

In order to obtain the independent holograms, the diffusing screen was moved continuously perpendicular to the optical axis of a CCD sensor for 15 times and thus 15 uncorrelated holograms are able to be captured by CCD.

The occlusion attacks often exist in data transfer process. For this, the simulation of occlusion attacks was conducted for both I_E and I_M holograms. Within the simulation, the occlusion area is the length of the hologram and the width of the occlusion is selected as shown in Figure 4(a).

The robustness of encryption of decryption against Gaussian noise was also validated for both the hologram I_E and I_M. A computer simulated Gaussian noise is used as shown in Figure 4(b).

5. Experimental Results

5.1. Encryption and Decryption Results

The intensities of holograms and are shown in Figure 5(a) and Figure 5(b). The 3D object was successfully reconstructed with speckle noises Figure 5(c). The 3D object was reconstructed without speckle noises Figures 5(d)-(f) show the decrypted images when either key was incorrect.

The reconstructed images at different distances are shown in Figure 6. When the reconstruction distance was 410 mm, the upper dice is out of focus while the lower one is on focus. The focus of this was switched when the reconstruction distance was 480 mm.

5.2. The Robustness against Occlusion and Noise Attacks

The results of robustness against occlusion and noise attacks are presented below. Correlation coefficient (CC) was used to evaluate the decrypted image quality between the reconstructed images without occlusion attacks and the reconstructed images with occlusion attacks.

With speckle noises, the results of reconstructed objects with 70% and 90% occluded Figure 7(a) and Figure 7(b). Without speckle noises, for same occlusions, the results are shown in Figure 7(c) and Figure 7(d). The relationships between CC and occlusion, with and without reducing noises, are shown in Figure 7(e) and Figure 7(f). The CC of reducing the speckle noise is lager when the same occlusion ratio is done from Figure 7(e) and Figure 7(f). As a result, reducing the speckle noise with the method of intensity superposition can mitigate the impact of occlusion on the quality of reconstructed object.

With speckle noises, the reconstructed object from with Gaussian noise of mean 0 and variance 0.0015, mean 0 and variance 0.002 in Figure 8(a) and Figure 8(b). Without speckle noises, the results under same noises are shown in Figure 8(c) and Figure 8(d). The relationships between CC and Gaussian noise with/without reducing speckle noises are shown in Figure 8(e) and Figure 8(f). Reducing the speckle noise with the method of intensity superposition can mitigate the impact of Gaussian noise on the quality of reconstructed object from Figure 8(e) and Figure 8(f).

6. Conclusions

A tangible 3D object information encryption and decryption method was proposed in this research. The encryption process started at recording encrypted 3D object and key holograms. Multiplication of the first and the conjugate of second extracted information from the holograms was performed, which followed by inverse Fourier transform to get the 3D object wave on the hologram plane. The Fresnel transform was then used for reconstructing decrypted images. The robustness of the method was tested against occlusion attacks and Gaussian noises.

Results showed that the 3D objects were successfully encrypted, decrypted, and reconstructed. The speckle noise reduction is evident through the multiple images superposition method. The 3D object can also be reconstructed at different diffraction distances. Additionally, the proposed method is also robust against occlusion attacks and Gaussian noise pollution.

In distinction from the previous research, a tangible 3D object was utilized for encryption and decryption. Only two holograms are needed for encryption, whereas the previous research often involved using multiple

holograms. Additionally, this method encrypts both object and reference light wave, which can possibly increase the security of the encryption. Potentially, the results of this research can find its applications in real 3D encryption and decryption.

Limitations also exist in this study. The proposed method is still not able to be used to encrypt large 3D object due to the limited resolution of CCD camera used for recording holograms. Furthermore, we have not yet analyzed the 3D coordinates of the objects, which can be investigated in the future.

Acknowledgements

This work was supported by National Natural Science Foundation of China (No. 61377010)

Cite this paper

YinghongLiu,WeiminJin,XinYang,DiWu,HongboZhang, (2015) A Robust Optical Encryption Method for Three-Dimensional Object Based on the Fresnel Transform. Optics and Photonics Journal,05,313-319. doi: 10.4236/opj.2015.511029

References

NOTES

^*Corresponding author.