Optics and Photonics Journal
Vol.05 No.09(2015), Article ID:60125,21 pages
10.4236/opj.2015.59026
Propagation Properties of Finite Olver-Gaussian Beams Passing through a Paraxial ABCD Optical System
Salima Hennani, Lahcen Ez-Zariy*, Abdelmajid Belafhal*
Laboratory of Nuclear, Atomic and Molecular Physics, Department of Physics, Faculty of Sciences, Chouaïb Doukkali University, Jadida, Morocco
Email: *ezzariy@gmail.com, *belafhal@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 3 August 2015; accepted 27 September 2015; published 30 September 2015
ABSTRACT
In this paper, an exact analytical propagation formula of Finite Olver-Gaussian Beams (FOGBs) passing through a paraxial ABCD optical system is developed and some numerical examples are performed. The propagation properties of the FOGBs through general optical systems characterized by given ABCD matrix are studied on the basis of the generalized Huygens-Fresnel diffraction integral, which permits to show the behavior of this laser beams family and its properties depending of the laser parameters. This research is of interest to prove some investigations done in the past by other researchers.
Keywords:
Finite Olver-Gaussian Beams, Generalized Huygens-Fresnel Diffraction, ABCD Optical Systems

1. Introduction
More freshly, Belafhal et al. [1] have introduced the so-called Olver beams as a novel beams family of non- diffracting beams. The authors have demonstrated that this class of beams is a solution of Schrödinger and Helmholtz equations. Like the other nondiffracting beams [2] , Olver beams require an infinite energy and propagate in the free space without distortion. Thus, the Olver beams are not realizable in practice. So, a truncation of these beams by a finite aperture or its modulation by a Gaussian envelope is very indispensible to create the pseudo-nondiffracting finite Olver beams or the Olver-Gaussian beams. Yet, in their recent work, Belafhal and their co-authors [1] have proposed the masks to generate the finite-energy Olver beams. In the same study [1] , the investigators have proved that the Olver beams as a generalization of the ordinary Airy beams are considered as the zeroth-order Olver beams.
On the other hand, the studies of the diffraction of apertured and unapertured laser beams by optical systems including aligned and misaligned ones and through turbulent media, are very vital to physical optics and propagation properties of the studied beams whatever Gaussian, nondiffracting or quasi-nondiffracting beams. For this purpose, several literature researches are elaborated within the context [3] -[17] . Among them, Belafhal and Dalil- Essakkali [7] have investigated the propagation characteristics of the Bessel-Gaussian and the Quadrature Bessel- Gaussian beams through an ABCD optical system. The Mathieu modulated by Gaussian and flattened Gaussian beams through aligned, misaligned optical systems and turbulent media have been examined theoretically and numerically by many authors [13] [14] . In 2004, Bandres et al. [18] and López-Mariscal et al. [19] have analyzed the features of the nondiffracting parabolic beams theoretically and experimentally, respectively. Many studies have been interested in the properties of pseudo-nondiffracting beams through other optical systems such as Kerr media [20] [21] , and crystals [22] [23] . Airy beams which are regarded as the zeroth-order Olver beams attract the attention of a lot of scientists of the laser community [24] -[30] . These zeroth-order Olver (Airy) beams have been the subject of many other studies in various optical systems, be it aligned, misaligned, turbulence, crystal, Kerr media [31] -[36] or others. More recently, Liu et al. [37] have obtained an approximate analytical expression for the propagation of an Airy-Gaussian beams passing through an ABCD optical system with a rectangular annular aperture. Our research group contributes in investigation of the properties of these beams class passing through a rectangular annular apertured ABCD optical system [38] and through a misaligned one [39] .
The diffraction features of the Finite Olver beams (FOBs) and the Finite Olver-Gaussian beams (FOGBs) by optical systems have not been studied elsewhere. The current paper is the first one of a series of works that are interested in the treatment of the Olver beams family in aligned or misaligned optical systems, turbulence, crystals and others which are within the interest of our research group. In the actual work, we start the series by a theoretical and numerical examination of the propagation properties of FOGBs through a simple paraxial ABCD optical system. An analytical formula is developed in the coming section using the Collins diffraction integral formula. Some special cases correspond to the Finite Airy-Gaussian beams, FOBs, Olver-Gaussian beams and Airy-Gaussian beams passing through an ABCD optical system are derived from our main finding in Section 3. Several numerical calculations are performed in Section 4 to analyze the action of some parameters on the transverse intensity distribution and shape of the beams class exiting the ABCD optical system. A simple conclusion is Plainfield in Section 5 of the paper.
2. FOGBs Passing through a Paraxial ABCD Optical System
The propagation of the light beam passing through a paraxial optical system, described by an ABCD matrix, obeys to the generalized Huygens-Fresnel integral, which connects the output electric field 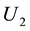 with the input one
with the input one 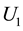 [40]
[40]
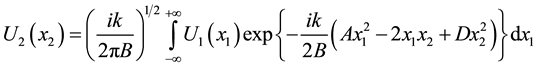 , (1)
, (1)
where 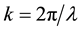 is the wave number and
is the wave number and 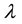 being the wavelength. A, B, C and D are the ray matrix elements.
being the wavelength. A, B, C and D are the ray matrix elements.
In the Cartesian coordinates system, the incident electrical field distribution of Finite Olver-Gaussian beam is given by [1]
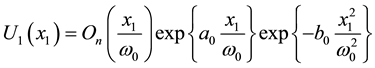 , (2)
, (2)
where 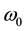 is the spot size of the fundamental Gaussian mode.
is the spot size of the fundamental Gaussian mode. 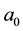 is the truncation parameter and
is the truncation parameter and 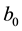 is a constant coefficient to be equal to 0 or 1.
is a constant coefficient to be equal to 0 or 1. 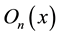 is the nth-order Olver function of real x with n = 0; 1; 2; …
is the nth-order Olver function of real x with n = 0; 1; 2; …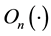 is defined by the following integral representation [1]
is defined by the following integral representation [1]
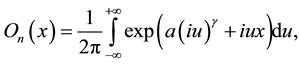 (3)
(3)
with
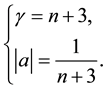 (4)
(4)
Introducing Equation (2) and Equation (3) into Equation (1) and recalling the integral formulas [1] [41]
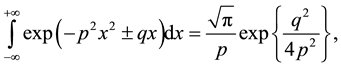 (5)
(5)
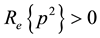 , and
, and
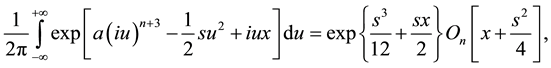 (6)
(6)
and after some calculations, the final analytical expression of the output electrical field expression of FOGBs is given by

This is the main result of this paper; it permits us to study the propagation properties of FOGBs through any ABCD optical system. It is to note that the output beam is of the same family as the input beam. This finding is regarded as a generalization of several studies of literature which are derived as particular cases of our investigation.
3. Particular Cases
1) Ordinary Finite Airy-Gaussian Beams through an ABCD Optical System
This case is obtained when

By the use of Equation (7) and under the above condition, the output electrical field of the Finite Airy- Gaussian beam travelling any ABCD optical system reads to

This result is similar to that found by Bandres et al. [18] .
2) Olver-Gaussian Beams through an ABCD Optical System
This case can be obtained when

This beam passes through an ABCD optical system to give another beam of the same family where its form is obtained from Equation (7) by replacing a0 by 0 and is expressed as

Yet, if 


This result is a particular case, when
3) Finite Olver Beam through an ABCD Optical System
When

Under this condition, the output electrical field of the Finite Olver beams through an ABCD optical system is given by

If 


which corresponds to a Finite Airy beam. The output field of this beam through an ABCD is deduced from our principle result established in Equation (7) taking into account the parameters chosen above and it is expressed as

This expression is the same of the principle result of Ref. [32] .
4. Numerical Calculations and Analysis
Equation (7) will be simulated numerically in three particular cases: Fractional Fourier Transform (FFT) system, Free space system and Thin Lens system.
1) FOGBs through a FFT System
The transfer matrix corresponding to a FFT system is given by:

with

The intensity distribution of the Finite zeroth-order Olver-Gauss beams is illustrated numerically in Figure 1 and compared with that given in Ref. [32] concerning the properties of Finite Airy beams passing through a FFT system.


Figure 1. Intensity distribution of zeroth FOGBs through a FFT system with different fractional orders: P = 0.4, 0.8 and 1.2 with (a) b0 = 0 and (b) b0 = 1.
In Figure 2 and Figure 3, we plot the intensity profile of the Finite Olver Beams in the first and second beam orders (n = 1, 2), which allows us to examine the effect of b0 (b0 = 0 and 1) and Fractional order P on the propagation characteristics of Olver beams through a FFT optical system. The calculations parameters, used in the compilation of these figures, are:



From the plots of Figure 3, it appears that the intensity distribution is the same for the values of the FFT orders P = 0.4 and P = 0.8. For these values, we remark that the secondary lobes of the Finite Olver beams are situated in the negative x-directions. However, the oscillations of the considered beams are displaced towards the positive part of the transverse x-coordinate when the FFT order P takes the value 1.2. The oscillations of the Olver beams totally disappear with the presence of the Gaussian term in Figure 3(b) whatever the FFT order P. This is could be more evident, because the rule of the Gaussian envelope, already, is to avoid the oscillations presented by the nondiffracting beams.
2) FOGBs through a Free Space
The transfer matrix which represent the Free Space of the axial distance z is found to be given as

From Equation (7), one obtains the output field as:

In Figure 4, we give the output intensity distribution of FOGBs through a Free space optical system at propagation distance z = 1000 mm with a0 = 0.1 for the beam order n = 2 and for two values of ω0: 4 and 12 mm. From this figure one can deduced that the amplitude profile of the intensity distribution expands completely with an increase of the beam spot size with seeing the effect of the Gaussian parameter b0. It can be seen that much as ω0 increases as the beam spot becomes wider either with or without Gaussian term. Always, the secondary lobes vanish if the Finite Olver beams are modulated by a Gaussian envelope.
Figure 5 depicts the output intensity distribution of FOGBs of different orders, n = 2, through a free space, for each order, at propagation distances 

3) FOGBs through a Thin Lens
We consider an optical system formed with a thin lens followed by a free space. The matrix corresponding to the considered optical system is characterised by

In this case, the output field can be written as


Figure 2. Intensity distribution of FOGBs of order n = 1 through a FFT system with different fractional orders: P = 0.4, 0.8 and 1.2 with (a) b0 = 0 and (b) b0 = 1.


Figure 3. Intensity distribution of FOGBs of order n = 2 through a FFT system with different fractional orders: P = 0.4, 0.8 and 1.2 with (a) b0 = 0 and (b) b0 = 1.


Figure 4. Intensity distribution of FOGBs of order n = 2 through free space system with two values of




Figure 5. Intensity distribution of FOGBs of order n = 2 through a free space system with two values of z (in mm) and (a) 


In Figure 6 and Figure 7, we plot the amplitude of the intensity distribution of Finite Olver-Gaussian beams


Figure 6. Intensity distribution of zeroth FOGBs through a thin lens system with two values of f with (a) b0 = 0 and (b) b0 = 1.


Figure 7. Intensity distribution of FOGBs of order n = 2 through a thin lens system with two values of f with (a) b0 = 0 and (b) b0 = 1.
through thin lenses of focal lengths f = 150 mm, 200 mm and 500 mm, respectively. According to the graphs of these figures, the choice of f acts mostly on the propagation distance of the beam. Also, one remarks that the Gaussian term has a major effect on the elimination of secondary lobes of the beam leaving the thin lens outgoing. The side lobes totally vanish for b0 = 1. From the illustrations of these figures, it is provided that as far as the thin lens focal length f increases as much as the spot width of the beam leaving the thin lens deceases. Usually, the oscillations of the beam exiting in the thin lens disappear with a modulation of the Finite Olver beams by a Gaussian transmittance.
The numerical simulations performed above show that the secondary lobes present in the intensity distribution of a FOGBS, at the receiver plane optical system, vanish with the presence of the Gaussian modulation whatever the FOGBs order and whatever the optical system.
5. Conclusion
In this study, by means of the Collins diffraction integral formula, a general exact analytical expression of the properties of the propagation of a Finite Olver-Gaussian beam through any paraxial complex ABCD optical sys- tem is developed. This formula considered the main finding of the work is applied for the Fractional Fourier transform, the free space and the thin lens as examples of optical systems and three analytical expressions are developed, respectively. The properties of Finite Airy-Gaussian, Finite Olver, Finite Airy, Olver-Gaussian, Airy-Gaussian beams traveling an ABCD optical system are derived as particular cases of our principle investi- gation. In order to examine the impact of some parameters, such as the propagation distance, the fractional dis- tance and the focal length on the propagation characteristics of the FOGBs through the above optical systems, several numerical calculations are performed in the study. The obtained formulae developed in the present work form the basis for the propagation of an important beams family through any paraxial complex ABCD optical system and can be extended in a future study to any medium as misaligned optical systems or turbulent atmos- phere.
Cite this paper
SalimaHennani,LahcenEz-Zariy,AbdelmajidBelafhal, (2015) Propagation Properties of Finite Olver-Gaussian Beams Passing through a Paraxial ABCD Optical System. Optics and Photonics Journal,05,273-294. doi: 10.4236/opj.2015.59026
References
- 1. Belafhal, A., Ez-Zariy, L., Hennani, S. and Nebdi, H. (2015) Theoretical Introduction and Generation Method of a Novel Nondiffracting Waves: Olver Beams. Optics and Photonics Journal, 5, 234-246.
http://dx.doi.org/10.4236/opj.2015.57023 - 2. Gutiérrez-Vega, J.C. and Bandres, M.A. (2005) Helmholtz-Gauss Waves. Journal of the Optical Society of America A, 22, 289-298.
http://dx.doi.org/10.1364/JOSAA.22.000289 - 3. Guizar-Sicairos, M. and Gutiérrez-Vega, J.C. (2006) Generalized Helmholtz-Gauss Beam and Its Transformation by Paraxial Optical Systems. Optics Letters, 31, 2912-2914.
http://dx.doi.org/10.1364/OL.31.002912 - 4. Ding, G.L. and Lü, B.D. (2003) Decentered Twisted Gaussian Schell-Model Beams and Their Propagation through a Misaligned First-Order Optical System. Optical and Quantum Electronics, 35, 91-100.
http://dx.doi.org/10.1023/A:1022478608090 - 5. Gu, J.G., Zhao, D.M., Mei, Z.R. and Mao, H.D. (2004) The Relative Phase Shift of Off-Axial Gaussian Beams through an Apertured and Misaligned Optical System. Optik-International Journal for Light and Electron Optics, 115, 187-191.
http://dx.doi.org/10.1016/S0030-4026(08)70009-3 - 6. Cai, Y.J. and Lin, Q. (2004) Light Beams with Elliptical Flat-Topped Profiles. Journal of Optics A: Pure and Applied Optics, 6, 390-395.
http://dx.doi.org/10.1088/1464-4258/6/4/015 - 7. Belafhal, A. and Dalil-Essakkali, L. (2000) Collins Formula and Propagation of Bessel-Modulated Gaussian Light Beams through an ABCD Optical System. Optics Communications, 177, 181-188.
http://dx.doi.org/10.1016/S0030-4018(00)00600-3 - 8. Wang, X.Q. and Lü, B.D. (2002) The Beam Propagation Factor and Far-Field Distribution of Bessel-Modulated Gaussian Beams. Optical and Quantum Electronics, 34, 1071-1077.
http://dx.doi.org/10.1023/A:1021160303678 - 9. Mei, Z.R., Zhao, D.M., Wei, X.F., Jing, F. and Zhu, Q.H. (2005) Propagation of Bessel-Modulated Gaussian Beams through a Paraxial ABCD Optical System with an Annular Aperture. Optik—International Journal for Light and Electron Optics, 116, 521-526.
http://dx.doi.org/10.1016/j.ijleo.2005.05.003 - 10. Zhao, C.L., Wang, L.G., Lu, X.H. and Chen, H. (2007) Propagation of High-Order Bessel-Gaussian Beam through a Misaligned First-Order Optical System. Optics & Laser Technology, 39, 1199-1203.
http://dx.doi.org/10.1016/j.optlastec.2006.08.015 - 11. Zhou, G.Q. (2010) Propagation of a Lorentz-Gauss Beam through a Misaligned Optical System. Optics Communications, 283, 1236-1243.
http://dx.doi.org/10.1016/j.optcom.2009.12.006 - 12. Dartora, C.A. and Hernández-Figueroa, H.E. (2004) Properties of a Localized Mathieu Pulse. Journal of the Optical Society of America A, 21, 662-667.
http://dx.doi.org/10.1364/JOSAA.21.000662 - 13. Chafiq, A., Hricha, Z. and Belafhal, A. (2005) Paraxial Propagation of Mathieu Beams through an Apertured ABCD Optical System. Optics Communications, 253, 223-230.
http://dx.doi.org/10.1016/j.optcom.2005.04.068 - 14. Chafiq, A., Hricha, Z. and Belafhal, A. (2007) Flat-Topped Mathieu-Gauss Beam and Its Transformation by Paraxial Optical Systems. Optics Communications, 278, 142-146.
http://dx.doi.org/10.1016/j.optcom.2007.05.042 - 15. Ez-Zariy, L., Nebdi, H., Chafiq, A. and Belafhal, A. (2012) Mathieu-Gauss Beam and Its Propagation. Physical and Chemical News, 64, 42-52.
- 16. Ez-Zariy, L., Zouhal, B., Nebdi, H. and Belafhal, A. (2012) Generalization of the Transformation of Flat-Topped Mathieu-Gauss Beams by Paraxial Optical Systems. Physical and Chemical News, 65, 9-17.
- 17. Eyyuboglu, H.T. (2008) Propagation Aspects of Mathieu-Gaussian Beams in Turbulence. Applied Physics B, 91, 611-619.
http://dx.doi.org/10.1007/s00340-008-3020-8 - 18. Bandres, M.A., Gutiérrez-Vega, J.C. and Chávez-Cerda, S. (2004) Parabolic Nondiffracting Optical Wave Fields. Optics letters, 29, 44-46.
http://dx.doi.org/10.1364/OL.29.000044 - 19. López-Mariscal, C., Bandrés-Motola, M., Gutiérrez-Vega, J.C. and Chávez-Cerda, S. (2004) Experimental Realization of Nondiffracting Parabolic Beams. Diffractive Optics and Micro-Optics, Optical Society of America, Paper DMA7.
http://dx.doi.org/10.1364/domo.2004.dma7 - 20. Khilo, N.A. (2013) Conical Diffraction and Transformation of Bessel Beams in Biaxial Crystals. Optics Communications, 286, 1-5.
http://dx.doi.org/10.1016/j.optcom.2012.07.030 - 21. Tang, B. (2009) Hermite-Cosine-Gaussian Beams Propagating in Uniaxial Crystals Orthogonal to the Optical Axis. Journal of the Optical Society of America A, 26, 2480-2487. http://dx.doi.org/10.1364/JOSAA.26.002480
- 22. Magni, V., Cerullo, G. and De Silvestri, S. (1993) ABCD Matrix Analysis of Propagation of Gaussian Beams through Kerr Media. Optics Communications, 96, 348-355.
http://dx.doi.org/10.1016/0030-4018(93)90284-C - 23. Chen, C.D., Chen, B., Peng, X. and Deng, D.M. (2015) Propagation of Airy-Gaussian Beam in Kerr Medium. Journal of Optics, 17, Article ID: 035504.
http://dx.doi.org/10.1088/2040-8978/17/3/035504 - 24. Berry, M.V. and Balazs, N.L. (1979) Non-Spreading Wave Packets. American Journal of Physics, 47, 264-267.
http://dx.doi.org/10.1119/1.11855 - 25. Siviloglou, G.A., Broky, J., Dogariu, A. and Christodoulides, D.N. (2007) Observation of Accelerating Airy Beams. Physical Review Letters, 99, Article ID: 213901.
http://dx.doi.org/10.1103/PhysRevLett.99.213901 - 26. Siviloglou, G.A. and Christodoulides, D.N. (2007) Accelerating Finite Energy Airy Beams. Optics Letters, 32, 979-981.
http://dx.doi.org/10.1364/OL.32.000979 - 27. Kaganovsky, Y. and Heyman, E. (2010) Wave Analysis of Airy Beams. Optics Express, 18, 8440-8452.
http://dx.doi.org/10.1364/OE.18.008440 - 28. Broky, J., Siviloglou, G.A., Dogariu, A. and Christodoulides, D.N. (2008) Self-Healing Properties of Optical Airy Beams. Optics Express, 16, 12880-12891.
http://dx.doi.org/10.1364/OE.16.012880 - 29. Polynkin, P., Kolesik, M., Moloney, J.V., Siviloglou, G.A. and Christodoulides, D.N. (2009) Curved Plasma Channel Generation Using Ultraintense Airy Beams. Science, 324, 229-232.
http://dx.doi.org/10.1126/science.1169544 - 30. Morris, J.E., Mazilu, M., Baumgartl, J., Cizmár, T. and Dholakia, K. (2009) Propagation Characteristics of Airy Beams: Dependence upon Spatial Coherence and Wavelength. Optics Express, 17, 13236-13245.
http://dx.doi.org/10.1364/OE.17.013236 - 31. Bandres, M.A. and Gutierrez-Vega, J.C. (2007) Airy-Gauss Beams and Their Transformation by Paraxial Optical Systems. Optics Express, 15, 16719-16728.
http://dx.doi.org/10.1364/OE.15.016719 - 32. Han, D.H., Liu, C.T. and Lai, X.Y. (2012) The Fractional Fourier Transform of Airy Beams Using Lohmann and Quadratic Optical Systems. Optics & Laser Technology, 44, 1463-1467.
http://dx.doi.org/10.1016/j.optlastec.2011.12.017 - 33. Wen, W., Lu, X.Y., Zhao, C.L. and Cai, Y.J. (2014) Propagation of Airy Beam Passing through the Misaligned Optical System with Hard Aperture. Optics Communications, 313, 350-355.
http://dx.doi.org/10.1016/j.optcom.2013.10.056 - 34. Nelson, W., Palastro, J.P., Davis, C.C. and Sprangle, P. (2014) Propagation of Bessel and Airy Beams through Atmospheric Turbulence. Journal of the Optical Society of America A, 31, 603-609.
http://dx.doi.org/10.1364/JOSAA.31.000603 - 35. Zhou, G.Q., Chen, R.P. and Chu, X.X. (2012) Propagation of Airy Beams in Uniaxial Crystals Orthogonal to the Optical Axis. Optics Express, 20, 2196-2205.
http://dx.doi.org/10.1364/OE.20.002196 - 36. Zhang, Y.Q., Belic, M.R., Zheng, H.B., Chen, H.X., Li, C.B., Li, Y.Y. and Zhang, Y.P. (2014) Interactions of Airy Beams, Nonlinear Accelerating Beams, and Induced Solitons in Kerr and Saturable Nonlinear Media. Optics Express, 22, 7160-7171.
http://dx.doi.org/10.1364/OE.22.007160 - 37. Liu, H.L., Lü, Y.F., Xia, J., Pu, X.Y. and Zhang, L. (2015) Propagation of an Airy-Gaussian Beam Passing through the ABCD Optical System with a Rectangular Aperture. Optics Communications, 355, 438-444.
http://dx.doi.org/10.1016/j.optcom.2015.07.017 - 38. Ez-Zariy, L., Nebdi, H., Boustimi, M. and Belafhal, A. (2014) Transformation of a Two-Dimensional Finite Energy Airy Beam an ABCD Optical System with a Rectangular Annular Aperture. Physical and Chemical News, 73, 39-51.
- 39. Ez-Zariy, L., Hennani, S., Nebdi, H. and Belafhal, A. (2014) Propagation Characteristics of Airy-Gaussian Beams Passing through a Misaligned Optical System with Finite Aperture. Optics and Photonics Journal, 4, 325-336.
http://dx.doi.org/10.4236/opj.2014.411033 - 40. Collins, S.A. (1970) Lens-System Diffraction Integral Written in Terms of Matrix Optics. Journal of the Optical Society of America A, 60, 1168-1177.
http://dx.doi.org/10.1364/JOSA.60.001168 - 41. Gradshteyn, I.S. and Ryzhik, I.M. (1994) Tables of Integrals Series and Products. 5th Edition, Academic Press, New York.
NOTES
*Corresponding authors.


























