Received 25 June 2015; accepted 11 December 2015; published 15 December 2015

ABSTRACT

In this study, Octagonal Photonic Crystal Fiber (O-PCF) structures are designed for different air filling fractions with fixed pitch length of 2.2 µm. The light propagating characteristics of PCF structures such as effective refractive index, confinement loss, chromatic dispersion mode effective area and nonlinear coefficient are numerically analyzed. The simulation results show that the fibers have dispersion flattened, ultra-low loss highly nonlinear nature in the wavelength region 1.3 µm to 1.7 µm.

Keywords:

Photonic Crystal Fiber (PCF), Confinement Loss, Effective Mode Area, Chromatic Dispersion

1. Introduction

Photonic Crystal Fibers (PCFs) are a new class of optical waveguides which offer exceptional light guiding mechanism and deliver significantly improved performance compared to conventional optical fibers [1] - [3] . Custom-made design of various PCF geometries offers PCFs as a potential candidate for manipulating light through optical waveguides to achieve properties like dispersion compensation, low confinement loss, large mode area [4] , etc. In PCFs, anomalous dispersion can be achieved with a wavelength at which group velocity dispersion of pure silica and conventional single mode fiber is nominal. This peculiar property can be utilized for the modeling, simulation and demonstration of soliton propagation and super-continuum generation [3] - [7] . The important characteristics of PCF include endlessly single mode operation, high birefringence, and ultrahigh nonlinearity [8] -[10] .

Russel et al., in 1992 proposed this special type of fibers that consisted of intentionally made micro-structures in the form of periodic array of air-holes in either circular or in elliptical shape which might be in the form of hexagonal pattern. This will result in the periodic variation in refractive index around the fiber-core running down its length and the first PCF proto-type was reported in 1996 [2] . The most attractive feature of PCFs is the flexibility in designing the micro-structures (Photonic band gaps) in the dielectric material. This is the most important factor that determines the characteristic behavior of interaction between the photons and the dielectric material. It is possible to tune the wavelength range in PCFs by the geometry of periodic dielectric variations [11] [12] . The dimensions of the micro-structured elements are of the order of light wavelength propagating through the fiber. One can design micro-structures in optical materials so that propagation of light over certain range of frequencies can be inhibited and some other bands of frequencies can be allowed to propagate [13] - [15] . It can be seen the behavior of photons in periodically micro-structured dielectric materials and that of electrons in crystalline semiconductors are similar [16] .

2. Octagonal Photonic Crystal Fiber (O-PCF) Geometrical Parameters

In the present work, we have proposed a new class of index guided photonic crystal fibers with octagonal arrangement of air holes in the SiO₂ (refractive index 1.45) host material. The significant parameters for the PCF design are the diameter of the holes and the distance between adjacent holes called pitch (Λ). In the octagonal structure the basic unit is an isosceles triangle with vertex angle 450. The length of the identical legs is taken as the pitch. The length of the side opposite to the vertex angle, calculated from the formula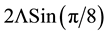, is the spacing between the air holes on the same ring. The octagonal symmetry in the cladding region is satisfied by repeating the unit isosceles triangle around the core. Air-holes are placed at each corner of the basic triangle. The key parameter of the PCFs design, the air filling fraction (AFF) is calculated using the fundamental relation AFF = A_hole/A_cell, where A_hole is the area of the air-hole inside the unit triangle and A_cell is the area of the unit triangle. In the present work O-PCF structures are designed for six different d/Λ values (d/Λ= 0.2, 0.3, 0.4, 0.5, 0.6, 0.7). In each structure the pitch length is fixed and its value is taken to be 2.2 µm. As the pitch remains constant, different air filling fraction is calculated by varying the size of the air hole and the calculated values are 0.088813, 0.199828, 0.355250, 0.555079, 0.799314 and 1.087954, respectively. It is found that for all the structure the fractional area of the three air holes occupied in the unit isosceles triangles is same and is equal to the 50% of the area of a single air hole. For the easiness of the simulation work only four ring PCF structures are considered.

3. Simulation Method and Equations

The propagation of electromagnetic radiations through the photonic crystal fiber is studied by the numerical technique full vectorial Finite Elemental Method (FEM). The studies are carried out over a radiation spectrum of wavelengths ranging from 800 nm to 2000 nm. The FEM technique is one of the advanced vectorial methods to study the light propagation characteristics in PCFs. In the present study we calculate the propagation of the electric vector through the fiber over the given wavelength range with the help of the software COMSOL Multiphysics 4.3. The full vector analysis of the fiber structure is done by calculating the propagation of electric vector through the fiber by solving an eigenvalue problem drawn from the Maxwell’s equations using FEM [17] in each triangular subspace in the area of the meshed fiber structure and effective refractive index (n_eff) of the PCF is obtained from the simulation result. The modified total internal reflection mechanism guide the radiation through the proposed PCFs. To lock the back reflection of the leaky modes into the core of the fiber structure a scattering boundary condition is applied around the cladding region of the PCF. Effective mode area (A_eff), confinement loss (Lc), Chromatic dispersion (D), Nonlinear coefficient (γ) and Numerical aperture (NA) can be obtained by using values of n_eff to the following equations.

3.1. Confinement Loss (Lc)

As the electromagnetic radiation propagating through the designed PCFs, a part of the incident energy is leaking out of the core through the air holes and between the air holes. This may referred to as the confinement loss in the PCFs. It is given by [18]

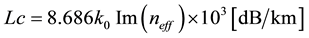(1)

where stands for the imaginary part of the effective refractive index and k₀ = 2π/ʎ, the free space wave number. Lc can be controlled by the proper selection of the dimension of air hole, pitch and the number of rings around the core. The confinement loss can also be reduced by simply increasing the index contrast between the core and cladding. With the increase in air filling fraction the modes are become more confined inside the core and hence the confinement loss decreases. But as the wavelength increase the modes are more and more spreading out of the center core, so the loss increases with the wavelength.

3.2. Chromatic Dispersion (D)

Dispersion means the broadening of light pulses as they pass through the light pipe. The large refractive index contrast between the core and cladding introduces a number of dispersion properties in photonic crystal fibers. The chromatic dispersion in PCFs can easily be controlled by changing the hole diameter, pitch and air holes arrangement i.e. cladding pattern. The total dispersion or chromatic dispersion of the PCF is the sum of the two components material dispersion and wave guide dispersion and is given by [18]

(2)

where Re(n_eff) is the real part of effective refractive index, ʎ is the wavelength and c is the velocity of electromagnetic waves in vacuum. The material dispersion of the silica that calculated from the Sellmeier’s formula is directly included in the FEM calculation.

3.3. Effective Mode Area (A_eff)

Effective mode area is an important functional parameter that determines optical performance of PCF, which is strongly depends on the core area and the core cladding index contrast and is given by [18]

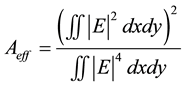(3)

where E is the transverse component of the electric field propagating inside the fiber.

3.4. Nonlinear Coefficient (γ)

The nonlinear coefficient of PCF is calculated from the formula [19]

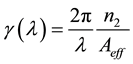(4)

where n₂ is the nonlinear part of the refractive index. From the relation it is clear that the non linear coefficient of the PCF is inversely related to the effective area. So the effective area is an important parameter in determining the nonlinearity in PCF.

3.5. Numerical Aperture (NA)

The Numerical aperture (NA) of a PCF is related to the effective area through the relation [19]

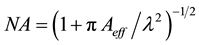(5)

4. Simulation Results and Discussion

4.1. Effective Refractive Index (n_eff)

Light propagation through the proposed solid core O-PCF for d/Λ-0.7 is shown in Figure 1, Figure 2 shows that the variation of the real part of effective index with the operating wavelength for fibers of different d/Λ ratios. At shorter wavelengths n_eff is converging towards the refractive index of silica and the modes are tend to be

more confined in the core part due to its waveguide structure, but as the wavelength increases the n_eff diverge. At higher wavelengths and d/Λ values the slope of the curves increases negatively. The value of n_eff decreases with increase in d/Λ values.

4.2. Confinement Loss (Lc)

Figure 3 shows the variation of confinement loss with d/Λ values for different operating wavelengths and Figure 4 shows the relationship between confinement loss and operating wavelength for the O-PCF d/Λ-0.7 It can be seen that confinement losses of the proposed structures increases with the operating wavelength and decreases with the d/Λ values. Since O-PCFs consist of more number of air holes compare to the hexagonal PCFs for the same ring number, the confinement loss of O-PCFs is considerably less. At the operating wavelength 1.55 µm the structures d/Λ-0.5, 0.6 and 0.7 are shown very low leakage losses and are 1.2022 × 10⁻² dB/km, 7.7043 × 10⁻⁶ dB/km and 6.90186 × 10⁻⁷ dB/km respectively.

4.3. Chromatic Dispersion (D)

Figure 5 Shows the chromatic dispersion properties of the proposed O-PCFs. It can be seen that the fiber with d/Λ-0.2 shows normal dispersion till 1.7 µm and crosses zero dispersion line at 1.7 µm and after that shows anomalous dispersion. The fiber d/Λ-0.3 crosses the zero dispersion line twice around at 1.1 µm and 1.7 µm. Within this region it shows a dispersion flattened behavior and an anomalous dispersion of around 10 ps/ (nm・km) is obtained at 1.55 µm. The fiber structures with d/Λ 0.4 to 0.7 shows zero dispersion at lower wavelengths (<1 µm) and the PCF d/Λ-0.4 can be considered as a dispersion flattened fiber within the wavelength region 1.3 µm - 1.7 µm with an average dispersion of 55.27 ps/(nm・km). For all the structures the value of

chromatic dispersion increases with increase in d/Λ values. Also the zero dispersion wavelength can be shifted with the proper selection of air hole diameter and it can be shifted to visible region by increasing the hole size. The proposed O-PCFs with anomalous dispersion can be used as dispersion compensation fiber in the telecommunication lines. The Zero dispersion wavelength (ZDW) and dispersion at the operating wavelength 1.55 µm for all the structures are given in the Table 1.

4.4. Effective Mode Area (A_eff)

Figure 6 shows the variation of effective mode area with the incident wavelength for different d/Λ ratios. A_eff increases linearly with the wavelength and decreases with the d/Λ values. This is due to the fact that when the wavelength increases the modes are leaking through the air holes and in between them. This will enhance the effective area of the guiding modes. For our particular structures we are keeping the pitch value constant throughout the entire designed fibers. Hence increasing the air filling fraction results in increase of the air hole size. This will in turn increase the confinement of the guiding modes through the core; as a result the mode effective area decreases with the increase in air filling fraction. The value of A_eff depends largely on the core radius and the core cladding refractive index contrast. The value of A_eff of different structures at the operating wavelength 1.55 µm is shown in Figure 6. Variation of A_eff considerably affect the nonlinear property and the light gathering capacity of the PCFs.

4.5. Nonlinear Coefficient (γ)

Figure 7 shows the wavelength response of the nonlinear coefficient for the entire fiber structure. Nonlinear coefficient is an important parameter which determines the nonlinearity of PCFs. It is derived from the effective

area using the relation (5) and it is clear that γ is inversely related to A_eff. For the calculation of γ the nonlinear refractive index coefficient for silica is taken as n₂ = 3.09 × 10⁻²⁰ m²/W. Figure 8 gives variation of Effective Mode Area and Nonlinear coefficient with the d/Λ ratios for the proposed O-PCF, at the operating wavelength 1.55 µm. From the Figure 7 and Figure 8 it is observed that the nonlinear coefficient decreases with increase in wavelength and increases with increase in d/Λ values.

4.6. Numerical Aperture (NA)

Figure 9 shows the wavelength response of numerical aperture (NA) of proposed O-PCFs for different d/Λ ratios. NA increases with both the wavelength and the d/Λ ratios. At the operating wavelength 1.55 µm fiber with d/Λ-0.7 shows a NA of 0.39379, which is very much larger than the conventional fibers. Figure 10 shows the variation of numerical aperture and effective modal spot size with the different d/Λ ratios at the operating wavelength 1.55 µm. Effective modal spot size (w_eff) is a parameter obtained from the effective mode area of the PCFs from the relation. It is found that w_eff increases with the wavelength and decreases with the air

filling fraction. At the operating wavelength 1.55 µm structure with d/Λ-0.7 has a spot size of 1.15165 µm.

5. Conclusion

In this paper, Octagonal Photonic Crystal Fibers are designed and simulated for seven different air filling fractions with the help of the software COMSOL Multiphysics 4.3 by finite elemental method (FEM). All the structures

deliver Gaussian output. The wavelength response of fiber parameters such as confinement loss, effective mode area, chromatic dispersion, non-linearity coefficient and numerical aperture of the proposed fibers are thoroughly investigated. From the studies it is established that the proposed O-PCFs with higher air filling fractions have shown high nonlinearity, large numerical aperture, low confinement loss and dispersion flattened nature over the wavelength range 1.3 µm to 1.7 µm.

Cite this paper

G. DhanuKrishna,G.Prasannan,S. K.Sudheer,V.P. MahadevanPillai, (2015) Design of Ultra-Low Loss Highly Nonlinear Dispersion Flattened Octagonal Photonic Crystal Fibers. Optics and Photonics Journal,05,335-343. doi: 10.4236/opj.2015.512032

References

NOTES

^*Corresponding author.