Optics and Photonics Journal
Vol.06 No.03(2016), Article ID:65209,8 pages
10.4236/opj.2016.63006
Resolution of Two Unequally Bright Points of Apodized Optical Systems with Asymmetric Circular Antenna Arrays
Andra Naresh Kumar Reddy1,2*, Pagolu Shailaja1, Dasari Karuna Sagar2
1Department of Physics (H & S), CMR Institute of Technology, Telangana, India
2Optics Research Group, Department of Physics, University College of Science, Osmania University, Telangana, India

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 13 March 2016; accepted 27 March 2016; published 30 March 2016
ABSTRACT
Sparrow criterion of resolution is used for assessment of the resolution of two object points of apodized optical systems under incoherent illumination of light. Semicircular arrays of circular aperture with discrete asymmetric apodization have suppressed side-lobes and a narrower central peak in the image plane termed as PSF good side on alternatively the right and left of the strong spectral point facilitates to detect the presence of weak spectral point in the vicinity of bright spectral point. The results of investigations on optimum discrete pupil function with semicircular arrays on the intensity distributions in the composite image of two object points with widely varying in their intensities under various degree of coherence of illumination have been studied. Sparrow resolution limits and the dip in central intensity as function of degree of coherence of the illumination (γ), intensity ratio (α), degree of asymmetric apodization (b) and number of discrete elements in semicircular array (n). The efficiency of aperture functions is discussed in terms of these parameters. Pupil function capabilities in redistribution of energy in composite image of two object points in close vicinity have been verified for different considerations. Current study has found an improvement in two-point resolution characteristics compared to their unapodized counter part. Fourier analytical properties of an optical system are presented for evaluation of this practical problem.
Keywords:
Complementary Pupil Function, Diffraction, Two-Point Resolution, Discrete Asymmetric Apodization, Degree of Coherence, Sparrow Limit, Intensity Ratio, Superresolution

1. Introduction
Apodization referred as the elimination of optical side lobes in diffraction field so as to improve the spatial resolution of optical system for two coherent or incoherent object points separated by different distance. It was most widely studied classical problem in diffractive optics. Asymmetric apodization applied to apertures was proposed by Cheng and Siu et al. [1] [2] . The Point Spread Function (PSF) produced by such an apertures consisted of good side which provided narrowed and sharp central lobe and with suppressing sidelobes at cost of worsening its counterpart termed as band side: enhanced sidelobes and broadened central lobe. Their works can be considered as a significant breakthrough in apodization studies. Their studies are basis for current investigation. Asymmetric apodization applied to semicircular arrays of 2D aperture functions increases the intensity profile of incoherent composite image of two object points on left half axis being broadened and shifted while on right half axis, the intensity profile becomes narrower. This simultaneous effect is a clear evidence for superresolution phenomena. The studies in improving the two-point or two-line resolution are limited certainly by shaping and shading apertures [3] - [15] . The resolution of two points having unequally intensity has investigated under the partially illumination by using modified Sparrow criterion [3] . In continuation to his work, Asakura applied apodization technique in order to improve the resolution of two unequally bright points [4] . Karuna Sagar et al. investigated the modified Sparrow limits of resolution for two-line objects for defocused coherent optical systems with Hanning amplitude filters [5] . Karuna Sagar et al. studied effects of defocusing on the sparrow limits of apodized optical systems [6] . ANK Reddy et al. extensively studied two-point resolution of asymmetrically apodized optical systems with amplitude type super solvers [7] . Yang and Kostinski applied asymmetric apodization for imaging of extra solar planets [8] . A. J. Dekker proposed new criterion for optical two-point resolution of optical imaging system under any degree of illumination. Unlike classical Rayleigh criteria, new criterion takes account of the presence of errors and their estimation approach in observed intensity distribution [9] . In addition to this, Dekker et al. studied apodization process narrowing the main-lobe of Point Spread Function to improve the resolution in the sense of classical criteria [10] . C.W Helstrom [11] [12] investigated the resolution, resolvability and detection of incoherent objects by diffraction-limited optical systems. R. Barakat [13] investigated application of apodization to increase two-point resolution of incoherent optical systems by means of Sparrow criterion. Nayar and Verma [14] studied two-point resolution of Gaussian aperture in partially coherent light. R. Barakat and E. Levin [15] further continued their study on resolution of incoherent objects of apodized optical systems. Discrete asymmetric apodization can suppress sidelobes in intensity distribution and can be achieved by weight distributions among the discrete semicircular elements in the array of aperture. Coated plates with this kind asymmetric aperture functions facilitate to detect direct image of very weak point object in close proximity to a strong point object by transposing “good” and “bad” sides. Without this process, these weak point objects will be submerged in the sidelobes of former. The method is thus reliable to determine whether an object is in the vicinity of the main lobe or outside it. More precisely, an object will be confirmed to be within the main peak if the intensity of the signal is unchanged during the rapid swapping of the weight distribution of elements in the array. In this work we have investigated asymmetric apodization of discrete type which is useful for improving the resolution of composite image of optical system. It would be useful in communication engineering, optical grating design, telescopic observations and microscopic imaging etc.
2. Mathematical Formulation
Far Field Diffraction of Semicircular Arrays with Asymmetric Apodization (Figure 1)
Asymmetric apodization is studied for an array of equally separated sources of wavelets referred as semi-circular ring elements. It is assumed that all elements are in phase so that initially the phase is zero, since linear variation of phase only shifts the Point Spread Function (PSF) towards its left half axis without affecting its shape. For instance, there are n elements of separation d. The semi-circular array generates wavelets of wavelength λ have equal amplitude 1/n, whose interference can be distinguished as a PSF. To apply asymmetric apodization, the aperture function has modified into viz. certain number of new semicircular elements of separation d are added at the left hand side of central circular region of the aperture with amplitude a/n and phase
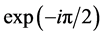 and complex amplitude
and complex amplitude . Similarly at the right hand side certain number of new elements with same amplitude 1/n but with opposite phase
. Similarly at the right hand side certain number of new elements with same amplitude 1/n but with opposite phase  with complex amplitude
with complex amplitude .
.
Figure 1. Illustration of the 2D-semi circular array of elements with discrete asymmetric apodization.
Further amplitude of left most elements are altered into  and similarly on right hand side elements are altered with amplitude of
and similarly on right hand side elements are altered with amplitude of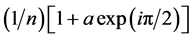 . The amplitudes and phase of other semi-
. The amplitudes and phase of other semi-
circular elements remain unchanged. Thus we consider 2D aperture with real amplitude transmittance central circular region and complex conjugated semicircular array of discrete elements at edges.
The diffraction field amplitude contributing by the circular aperture of radius (1-b):
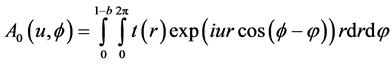 (1)
(1)
Complex amplitude contributing by left semi-circular array of discrete elements:
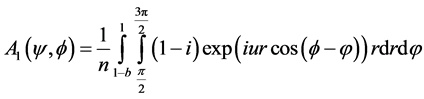 (2)
(2)
Complex amplitude contributing by right semi-circular array of discrete elements:
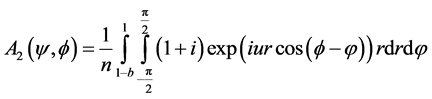 (3)
(3)
where 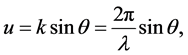 where
where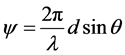 , d is the separation between elements. Total complex amplitude in the image plane is equal to sum of three components as
, d is the separation between elements. Total complex amplitude in the image plane is equal to sum of three components as 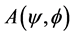 and the intensity PSF
and the intensity PSF 
which is the real measurable quantity can be obtained by taking square modulus of total complex amplitude in the image plane.
The quantities “a” and dimensionless diffraction coordinate “u” should be determined by optimization. Initially, asymmetric apodization of discrete type is applied to two-dimensional optical gratings and circular antenna arrays in which amplitude and phase of the resultant field can be recorded. The optimum values which depend only upon the number n of semi-circular elements in the array, and independent of λ and d. An optimum asymmetric pattern in composite image of two object points corresponding to given n and b (width of semi-cir- cular element) and it can be written as A(n, ψ) where n = 3, 5, 7, 9, 11, 13, ××× and b = 0.02, 0.04, 0.06, 0.08, 0.1.
According to simplified scalar wave-diffraction theory, the expression for composite image intensity distribution in image plane of an asymmetrically apodized optical system, as a function of reduced co-ordinate U, is given by:
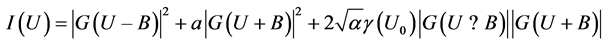 (4)
(4)
where 2B = U0 is the actual severance between the point sources, α is the ratio of their intensities and g(U0) is the true part of the complex degree of spatial coherence of the illumination. U is the dimension less diffraction co- ordinate in the image plane. G(U + B) and G(U ? B) are the normalized complex amplitude impulse response functions of the optical imaging system corresponding to the point sources, each of which is located at a distance of U0/2 on both side of the optical axis. The amplitude whim response function G(U ± B) is known by:

where J0 is the Bessel function of the first kind and zero order, t(r) is a transmittance for central circular region of the pupil function, here “r” is the distance of the reference point on the exit pupil uttered as a fraction of the radius of the pupil. The spatial distribution of transmittance in the plane containing exit aperture referred as the pupil function. Hence, the generalized expression for amplitude impulse response is given by:

The modified Sparrow criterion states that, “the resolution is retained when the second derivative of the image
intensity distribution vanishes at a certain point (
tion that this point 
zero”. This can be written as:


3. Results and Discussion
In order to improve the resolution of composite image of two object points with partially coherent light we proposed semicircular arrays with asymmetric apodization of discrete type. By means of Equation (4) the intensity distribution in composite image formed by the optical imaging system have been obtained as a function of optical coordinate U varying from −12 to +12 by employing a twelve-point Gauss quadrature numerical method of integration. It has been applied to find sparrow limits for semicircular edge ring width (b), different ratio of intensities (α) and degree of coherence (γ) and different no. of semicircular elements (n) in array. These values are obtained for unapodized case and asymmetrically apodized case. For n = 3, variation in resolution limit on composite image intensity distribution of two unequally bright object points produced by Airy (b = 0) and asymmetrically apodized (b ≠ 0) system under incoherent illumination of light has been depicted in Figure 2(a). A dip occurs clearly in all cases i.e. two point objects are well resolved for all values of b. As observed from the figure the dip position is shifting away from diffraction center with increase of semicircular ring width b of semicircular element in array of aperture.
The effect of point separation on composite image intensity distribution produced by asymmetrically apodized (b = 0.04) optical system illuminating with incoherent light has been depicted in Figure 2(b). It shows that, for Uo = 3 & 3.5 the composite image of two objects is likely to resolve and for other values of Uo the resolution of two unequally bright points is improved appreciably. In this study the resolution of optical system increases only for odd no. of semicircular edge ring elements in arrays where as for even no. of elements resolution is not considerably improved. Figure 2(c) demonstrates effect of no. of elements in array of aperture on the resolution limit. It is noticed that the points are resolved in all cases. Figure 2(d) and Figure 2(e) illustrates intensity pro-



Figure 2. Intensity distribution in the composite image of two objects points in different considerations: (a) As a function of asymmetric apodization parameter b under incoherent illumination (γ = 0) for odd no. of elements (n) in semi-circular array of aperture; (b) As a function of separation Uo of the two points for n = 3 and b = 0.04; (c) For different odd no. of elements (n) in semicircular array with semicircular ring width b = 0.04; (d) For different degree of coherence of illumination for two object points with widely varying intensities (α = 0.6); (e) Intensity distribution for different values of intensity ratio α for two point objects under incoherent illumination (γ = 0) for certain width (b) of semicircular rings in array over central circular region of aperture.
file curves of two points for different degree of coherence and intensity ratio respectively and other parameters are held constant. Figure 2(d) shows for lower values of γ, the two points are well resolved where as resolution is not found for the two points with coherent illumination of light. In other case the two object points with equal intensity under incoherent illumination of light are well resolved. Figure 3 shows that for α = 0.6 and b = 0.06, critical sparrow limits are obtained lower than that of unapodized case (b = 0) for any degree of coherence. Similar trend is noticed for b = 0.08 and b = 0.1. For higher values of b, the two point objects are highly resolved. In all above observations, a very interesting aspect is the two object points are resolved in different conditions without creating much disturbance to their lateral resolution so that proposed design is highly effective in two- point resolution studies.
HWHM as newly introduced image merit function for PSF, carries non-zero minima for higher values of semicircular ring width b. defined as: the distance from the centre of diffraction to where the intensity of main peak becomes 50% of its peak value. It can be seen in detail from Figure 4. For n = 1, 3 and 5, as semi-circular
Figure 3. Sparrow resolution limit (Uo) as a function of degree of coherence for different values of semicircular ring width “b” where n = 3 (odd number of semicircular elements).
Figure 4. FWHM, HWHM profile of apodized PSF.
edge ring width b increases the half maximum on good side decreases. For an instance for n = 3, HWHM on good side decreases from 1.6163 to 0.4076. In this case the resolution of optical system has been improved where as for n = 2, 4 and 6, resolution is degrading. This is important in the case of resolving the fade point object in the close vicinity of bright point. In addition to it, it is observed that for n = 3, HWHM on good side found with lower value than the value obtained in Airy case. On other hand, FWHM of PSF increases as b increases from 0 to 0.4 and then decreases on further increase in b value. However, the magnitude of this effect depends on number of odd discrete elements in semicircular array of pupil function and the semi-circular edge ring width b. This effect increases for b = 0.1 relative to Airy case. Whereas for b = 0.1 the asymmetry in PSF increased to large extent which is the basis for shift in main lobe of PSF towards left half axis of pattern, in which the dark region is occurring very close to the main lobe and occupied certain distance. This is a usual effect superresolover, improved by odd-number of elements in semicircular antenna array.
4. Conclusion
In conclusion, asymmetric apodization applied to semicircular arrays of 2D aperture can be a solution for real time model which can employ in optical systems design for imaging of two object points in close vicinity. It is found that for higher degree of asymmetric apodization the two point objects with widely varying intensities are fairly resolved for any degree of illumination of radiation. It can be verified that study is optimized for b = 0.04 (asymmetric apodization parameter) and n = 3, 5, (array with odd no. of discrete wavelet elements) due to 95% of side-lobe suppression is achieved on right hand side of image intensity distribution. The sparrow limit is found to minimum at b = 0.1 than that of clear aperture (Airy PSF). It can be fabricated in real practice with RF sputtering technology, in which suitable dielectric medium material vapors are deposited on substrate in the form of coating turns into complex pupil filters which can be integrated into real time imaging experiments to obtain asymmetric profile.
Cite this paper
Andra Naresh Kumar Reddy,Pagolu Shailaja,Dasari Karuna Sagar, (2016) Resolution of Two Unequally Bright Points of Apodized Optical Systems with Asymmetric Circular Antenna Arrays. Optics and Photonics Journal,06,39-46. doi: 10.4236/opj.2016.63006
References
- 1. Cheng, L. and Siu, G.G. (1991) Asymmetric Apodization. Measurement Science and Technology, 2, 198-202.
http://dx.doi.org/10.1088/0957-0233/2/3/002 - 2. Siu, G.G., Cheng, L., Chiu, D.S. and Chang, K.S. (1997) Asymmetric Apodization Applied to Linear Arrays. Journal of Physics D: Applied Physics, 30, 787-792.
http://dx.doi.org/10.1088/0022-3727/30/5/011 - 3. Asakura, T. (1974) Resolution of Two Unequally Bright Points with Partially Coherent Light. Nouvelle Revue d’Optique, 5, 169-177.
http://dx.doi.org/10.1088/0335-7368/5/3/304 - 4. Asakura, T. and Ueno, T. (1974) Apodization for Increasing Two-Point Resolution by the Sparrow Criterion under the Partially Coherent Illumination. Nouvelle Revue d’Optique, 5, 349-359.
http://dx.doi.org/10.1088/0335-7368/5/6/303 - 5. Karuna Sagar, D. and Bhikshamaiah, G. (2006) Defect of Focus in Two-Line Resolution with Hanning Amplitude Filters. Journal of Modern Optics, 53, 2011-2019.
http://dx.doi.org/10.1080/09500340600787507 - 6. Karuna Sagar, D., Sayanna, K.R. and Goud, S.L. (2003) Effects of Defocusing on the Sparrow Limits for Apodized Optical Systems. Optics Communications, 217, 59-67.
- 7. Reddy, A.N.K. and Karuna Sagar, D. (2013) Two Point Resolution of Asymmetrically Apodized Optical Systems. óptica Pura y Aplicada, 46, 215-222.
- 8. Yang, W. and Kostinski, A.B. (2004) One-Sided Achromatic Phase Apodization for Imaging of Extra Solar Planets. The Astrophysical Journal, 605, 892-901.
http://dx.doi.org/10.1086/382586 - 9. den Dekker, A.J. (1997) On Two Point Resolution of Imaging Systems. Periodica Polytechnica Mechanical Engineering, 41, 167-183.
- 10. den Dekker, A.J. and Van den Bos, A. (1997) Resolution: Survey. Journal of the Optical Society of America A, 14, 547-556.
http://dx.doi.org/10.1364/JOSAA.14.000547 - 11. Helstrom, C.W. (1969) Detection and Resolution of Incoherent Objects by a Background-Limited Optical System. Journal of the Optical Society of America, 59, 164-175.
http://dx.doi.org/10.1364/JOSA.59.000164 - 12. Helstrom, C.W. (1970) Resolvability of Objects from the Standpoint of Statistical Parameter Estimation. Journal of the Optical Society of America, 60, 659-666.
http://dx.doi.org/10.1364/JOSA.60.000659 - 13. Barakat, R. (1962) Application of Apodization to Increase Two-Point Resolution by Sparrow Criterion. I-Coherent Illumination. Journal of the Optical Society of America, 52, 276-283.
http://dx.doi.org/10.1364/JOSA.52.000276 - 14. Nayyar, V.P. and Verma, N.K. (1978) Two-Point Resolution of a Gaussian Aperture Operating in Partially Coherent Light Using Various Resolution Criteria. Applied Optics, 17, 2176-2180.
http://dx.doi.org/10.1364/AO.17.002176 - 15. Barakat, R. and Levin, E. (1963) Application of Apodization to Increase Two-Point Resolution by the Sparrow Criterion. II. Incoherent Illumination. Journal of the Optical Society of America, 53, 274-282.
http://dx.doi.org/10.1364/JOSA.53.000274
NOTES
*Corresponding author.





