Optics and Photonics Journal
Vol.05 No.04(2015), Article ID:55262,3 pages
10.4236/opj.2015.54009
A New Physical Model for the Vacuum Field Based on Einstein’s Stimulated Emission Theory
Richard A. Hutchin
Optical Physics Company, Calabasas, USA
Email: rahutchin@opci.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 28 February 2015; accepted 28 March 2015; published 31 March 2015
ABSTRACT
The vacuum electromagnetic field has been a mystery ever since Hedrik Casimir [1] proposed in 1948 that it actually existed and could be measured. Many subsequent experiments [2] have confirmed that its vast field strength (over a terawatt/cm2) is real and matches quantum predictions. Radiation pressures as high as 18 psi have been measured from the reflected vacuum light between plates of 10 nanometer separation. All of this creates a mystery. The electromagnetic field strength is more than a terawatt/cm2 everywhere in the universe and yet nothing is melted, ionized or burned up by the field. This paper extracts new insight from Einstein’s famous 1917 paper, credited with the discovery of stimulated emission and still believed today. The result is a practical explanation of the vacuum field and its observed properties.
Keywords:
Vacuum Field, Casimir Effect, Stimulated Emission

1. Introduction
The vacuum field was first suggested when the quantum mechanical solution for a harmonic oscillator predicted a lowest possible energy of 1/2hν rather than the expected zero. At first no one ascribed much reality to it, but it has become the subject of much research and theoretical modeling since Hedrik Casimir opened the door in 1948 [1] . He assumed the zero-point vibration energy (hν/2) of a quantum oscillator for each E & M mode frequency ν, and then he computed how much pressure the vacuum field would push on two parallel plates a distance d apart. Many experiments since then have verified this computation which matched the observed pressure of the vacuum between reflective plates [2] . They also have verified atomic effects of the vacuum field, such as the Lambe shift [3] , where the energy levels of S and P electron states shift their energy in response to these same vacuum fields. Still the mystery has remained about photonic fields that demonstrate terawatt/cm2 power in their ability to push and pull plates and bend electronic orbitals. How can such powerful fields produce none of the other usual photonic interactions, such as intense ionization of everything around us? No one has yet offered a physical understanding for the vacuum properties. We find two clues from Einstein’s 1917 paper on stimulated emission, which suggest a new model for the physical vacuum field.
2. Clues for the Vacuum Field
There are two key clues based on Einstein’s classic 1917 paper [4] on stimulated emission of a two state atom. The first one is quite commonly quoted in physics courses.
Clue 1: Blackbody radiation has a statistically equal ability to create excitation and stimulated emission proportional to the spectral intensity.
A more precise way to state Clue 1 is that the cross-section B12 for excitation from lower state 1 to upper state 2 equals the cross-section B21 for stimulated emission from upper state 2 to lower state 1.
Clue 2 comes from the same Einstein paper and is quite amazing, although it has been substantially ignored.
Clue 2: The spontaneous emission coefficient A21 has a simple physical relationship to the stimulated emission coefficient B21 given by:
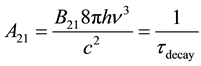 (1)
(1)
Together with some algebra and logic, these two clues carry us to a simple physical model for the vacuum field which explains its observed properties.
3. The Vacuum Field
The vacuum E & M field has the power spectral field density Ivac of Equation (2) when integrated over all directions (i.e. 4π steradians) [5] [6] .
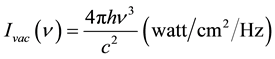 (2)
(2)
After the vacuum field was proposed to be observable by Hedrick Casimir in 1948 [1] , many experiments have confirmed that it has the expected field strength, which is measured by the pressure exerted on two closely spaced reflecting surfaces [2] . For radiation longer than 10 nm wavelength this vacuum field density is about 1.8 ´ 1012 watt/cm2―a huge intensity equal to the entire power generation of our world in 10 cm2. As a result of this massive electromagnetic intensity, the force from the pressure of light on two parallel plates a distance d apart is simply given by Equation (3), which computes to 18.85 psi for a separation d = 10 nanometers. The minus sign means that the force is squeezing the plates together, and since that force is proportional to 1/d4, it will be extremely important at atomic levels.
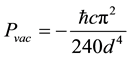 (3)
(3)
Ref [2] summarizes past research in over 200 pages, validating the Casimir force well.
The biggest mystery of the vacuum field is that it has the E & M field strength of 2 terawatt/cm2 (for wavelengths longer than 10 nm) but does not burn up everything as a normal E & M field of this strength would easily do. The conclusion is that the fields are there as predicted (because we measure their pressure), but they must have something different about them that prevents them from vaporizing everything.
The hint of this mysterious property we find in Clue 2, above, from Einstein’s paper on stimulated emission.
Clue 2: The spontaneous emission coefficient A21 has a simple physical relationship to the stimulated emission coefficient B21 given by:
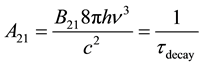 (4)
(4)
In words this result from Einstein’s paper says:
The spontaneous decay of any atom is identical to stimulated emission from a background spectral intensity equal to twice the vacuum background given in Equation (2) (4πhν3/c2).
We suggest that this relationship between spontaneous emission and the vacuum field is an important physical linkage. The logic we propose is the following:
Vacuum Hypothesis: Light comes in two independent and separable forms, up stimulating (excitation) and down stimulating (stimulated emission), with the vacuum form being purely down stimulating.
This means that the vacuum field will have the field strength that is observed, but it has an additional quality that makes it purely down stimulating and is thus unable to excite electronic states.
Now we return to Clue 1, which says that blackbody light has, on average, an equal ability to cause an up transition (excitation) as it does to cause a down transition (stimulated emission). Mathematically Einstein expressed this relationship as B12 = B21. Using this clue we ask how can the real fields of blackbody emission be divided into two equal components?one causing excitation and one causing stimulated emission? Our suggestion is to decompose all radiation into e+iwt and e−iwt components, where e+iwt is up stimulating (exciting) and e−iwt is down stimulating (stimulated emission). The sign convention is obviously arbitrary. When we look at power we get that half the power of a real field goes into the up-stimulating waveform and half into the down?an equal amount to each as required from Einstein’s paper with B12 = B21.
For instance, a real E&M field of the form 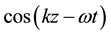 will decompose into up and down stimulating terms as shown in Equation (5). The mean-square-magnitude of the left side is 1/2, while the mean-square-magnitude of each of the right terms is 1/4. Note that the first term is purely e−iwt (down stimulating), while the second term is purely e+iwt (up stimulating)
will decompose into up and down stimulating terms as shown in Equation (5). The mean-square-magnitude of the left side is 1/2, while the mean-square-magnitude of each of the right terms is 1/4. Note that the first term is purely e−iwt (down stimulating), while the second term is purely e+iwt (up stimulating)
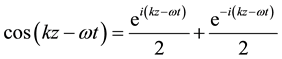 (5)
(5)
By separating out the + and − temporal frequencies, any real E & M field can be divided up into equal power levels of up and down stimulating forms. Using this principle, we rewrite Einstein’s results as follows:
The up-stimulating capability equals 2B12 times the power in the up stimulating component, and the down stimulating capability equals 2B21 times the power in the down stimulating component. Blackbody equilibrium requires that B12 = B21.
Since half the power of the real field goes into each up and down component, the final product is the same as he presented, but the interpretation has changed.
We can now apply this result to the vacuum field, which is purely down stimulating. We get that the ability of
the vacuum field to stimulate emission is 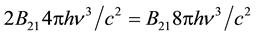 exactly as Einstein specified in Equa-
exactly as Einstein specified in Equa-
tion (1).
This logic suggests that all “spontaneous emission” is really stimulated emission from the vacuum field.
4. Summary
The vacuum field has been a mystery, which was generally ignored until Casimir challenged scientists to test its reality in 1948. [1] After hundreds of experiments [2] , we know the vacuum field is real and physical because it exerts pressure that matches its immense power density, and yet its phenomenal power density does not burn up anything at all. To resolve this inconsistency, we went through the following logic:
We considered the first term of Einstein’s 1917 paper [4] for spontaneous emission from an excited state and noted that it was identical to stimulated emission from a blackbody field equal to twice the vacuum field.
We then added the well known mathematical truth that any real sinusoidal field (such as a light wave) can be broken up into terms proportional to e+iwt and e−iwt, where each term has half the mean-square power of the real field.
Identifying e+iwt with excitation and e−iwt with stimulated emission, we pointed out that this identification supported Einstein’s second equality where up and down stimulation were equally strong in blackbody radiation (i.e. B12 = B21).
Finally, we rewrote Einstein’s equation for spontaneous decay as 2B21 times the down stimulating field strength. When we applied that equation to the the vacuum field, we got the identical quantitative result that Einstein derived for spontaneous emission?a result that is required for blackbody equilibrium and is still believed today.
We concluded that a possible physical model for the vacuum field is that it is a purely down stimulating form of light―which implies that the up and down stimulating qualities of light can be separated.
We also concluded that all spontaneous emission may actually be stimulated emission due to the vacuum field.
5. Conclusion
The physical model suggested here and anchored to Einstein’s blackbody equations from 1917 leads us to hypothesize that the up and down stimulating qualities of light may be separable. This would provide a simple, direct and consistent model for the vacuum field and interlocks with the very unusual (and generally ignored) relationship Einstein derived for spontaneous emission (Equation (2)). This model for the vacuum field is consistent with all measurements of the Casimir forces, which measure only the real part of the vacuum fields to create real forces. It also offers a practical explanation of the vacuum field and spontaneous emission.
References
- Casimir, H. (1948) On the Attraction between Two Perfectly Conducting Plates. Proc. Kon. Nederland. Akad. Wetensch., B51, 793-795.
- Bordag, M., Mohideen, U. and Mostepanenko, V.M. (2001) New Developments in the Casimir Effect. Physics Reports, 353, 1-205. (200+ page review paper) http://dx.doi.org/10.1016/S0370-1573(01)00015-1
- Lamb, W.E. and Retherford, R.C. (1947) Fine Structure of the Hydrogen Atom by a Microwave Method. Physical Review, 72, 241-243. http://dx.doi.org/10.1103/PhysRev.72.241
- Einstein, A. (1917) Zur Quantentheorie der Strahlung (On the Quantum Theory of Radiation). Physika Zeitschrift, 18, 121-128.
- Faria, A.J., Franca, H.M., Gomes, G.G. and Sponchiado, R.C. (2005) The Vacuum Electromagnetic Fields and the Schrödinger Picture. arxiv:quant-ph/0510134v2f. (Faria’s eq. 7 is the same as our equation 2, except in units of Joules/cm3/(radian per second). One must multiply by 2 to get Joule/cm3/Hz and then by c to get watt/cm3/Hz―the units that Einstein uses in his 1917 paper. Faria references Marshall below for a derivation based on 0.5 h of E&M energy per vacuum mode―the minimum energy for a quantum oscillator.)
- Marshall, T.W. (1963) Random Electrodynamics. Proceedings of the Royal Society A, 276, 475. http://dx.doi.org/10.1098/rspa.1963.0220

