Received 3 March 2015; accepted 18 March 2015; published 20 March 2015

ABSTRACT

In this paper, a biosensor based on photonic crystal fiber (PCF) is proposed and designed using Full-Vectorial Finite Element Method (FVFEM). The proposed PCF sensor consists of three concentric circles surrounding the core. The key optical sensor characteristics such as sensitivity, the field profiles and real part of the refractive index of the proposed PCF structure are investigated by employing the FVFEM. The proposed sensor can be deployed for environmental sensing when the PCF active region is filled with either analytes such as liquids or gas. By careful selection of the design parameters such as the radius of the sensing circle, the diameter of air holes in the core region and hole to hole spacing, Λ, the sensitivity analytes is determined. Our simulation results show that, the electric field distribution is primary localized in the third concentric circle with a radius of 16 µm. Effects of PCF bending on the sensitivity is also studied and reported.

Keywords:

Biosensors, Photonic Crystal Fibres Sensor, Nanosensor, Finite Element Method

1. Introduction

Photonic crystal fibers (PCFs), also called holey fibers or microstructured fibers have, undoubtedly, one of the most remarkable geometries available for the optical communications community. PCFs consist of air holes running parallel to its axis over the whole length. The guidance of light through these fibers is governed by the type of these structures. PCF usually consists of pure silica with an array of air holes in the cladding region. This structure creates band-gaps where propagation at certain optical frequencies is forbidden. The core is usually made by a defect in the periodic structure of the PCF cross-section. In PCFs, light can be guided either by the modified total internal reflection (TIR) or by the photonic band gap (PBG) effect.

Hollow core fibers allow light guidance by the photonic band gap (PBG), resulting in the ability to forbid propagation of the light in desired frequency range [1] -[4] . However in case of the solid core fibers, the light guidance can be achieved by total internal reflection. PCFs with solid core offer more design possibilities by varying the number of air holes in the cladding and lattice constant, leading to many applications that cannot be achieved with traditional optical fibers. The tremendous progress in telecommunication, materials processing and health services are increasing the demand for either chemical or biochemical sensing [5] of low index materials. Moreover, in sensing applications, using PCFs offers miniaturization, high degree of integration and remote sensing capabilities [5] [6] . Compared to conventional optical fibers, these microstructures exhibit a number of unusual properties, including single-mode operation at all wavelengths [7] , optical nonlinearity, high birefringence, and anomalous dispersion in the visible and near-infrared regions [8] [9] . Moreover, the optical gain provided by PCFs has under intensive study recently [10] . Therefore, PCFs can find wide application in many research areas, including telecommunications, sensing and medicine [7] .

In traditional evanescent optical fiber sensors, the detection is based on the several modifications such as plastic clad fibers, where a part of it should be removed to free direct interaction without medium. In PCF sensors, the interaction of the mode field and analytes depends on how strong they overlap. By considering PBG fiber, the light can be confined within the air core due to a two-dimensional PBG effect [11] -[15] . These PCF structures are promotion candidates in the area of sensing due to the fact that most of the guided modes propagate in the air regions of the fiber. In contrast to that PCFs suffer power propagation in the air regions. An alternative is to fill the air holes with analyte that increases considerably the interaction between guided mode fields and analytes. Therefore, designing of high sensitivity, and possibly selectivity, biosensors can be achieved by considering these type of PCF structures.

The air holes in PCF structure play a crucial role on the sensitivity of the sensor. On PCF based structures the analytes can reach the region where the mode field is located, resulting in a strong overlap. Such PCF sensor is robust since the cladding with coatings is not removed. Also, the presence of the air holes in the cladding section opens new opportunities for studying the interaction of light with liquids.

Due to the fact that these structures are able to control light into extremely small volumes, high local electromagnetic field intensities can be achieved. This phenomenon offers potential application to PCFs in sensing sectors. The major target area is biosensor where the detection and identification of biomolecular interactions, analytes and cells remain the main challenge facing the scientific community [16] [17] . The biosensor employs evanescent field sensing; where light is confined within the defect or/and core of the PCF, a fraction of the light extends outward into the out medium surrounding the core. Hence, the extended fraction of light can interact with analytes that entered the microstructure directly. PCF biosensors are able to detect the attachment of cells to the functionalized surfaces of a transducer because of the change in the refractive index that induces a variation in the optical properties of the light. A possible drawback is a quantification of the binding events; therefore the quantity of bound material and dynamics of the binding and unbinding reactions can be obtained [18] .

Surface plasmons, which are generated at the interface between a metal and dielectric, are very sensitive to the refractive index changes of the dielectric. Most of these sensors are based on the Kretschmann configuration [19] [20] . It is well known that this method implements a prism which allows the phase matching condition. However, the presence of the prism increases drastically the sensor dimensions, and its system complexity. In order to overcome that, PCFs can be implemented, which are able to offer high degree of integration and reduce significantly the size of the sensor. Also, another paramount advantage is that PCFs enable fluids to enter the air holes and interact directly with analytes.

In this study, a full vectorial finite element method (FEM) has been employed to investigate light propagation characteristics of the PCF. The modal solution approach based on FEM is more flexible and reliable than other techniques. It can represent any arbitrary cross-section more accurately and has been widely used to find the modal solutions of a wide range of optical waveguides [20] -[22] . The FEM formulation for modal analysis based on anisotropic perfectly matched layers (PML) is capable of handling as many modes as required and analyse the leaky modes. By using PMLs boundary condition, propagation characteristics of leaky modes in PCF can be accurately evaluated [21] . It should be noted that fabrication of the proposed PCF biosensor is not an issue any more due to advancement of current state-of-the-art of the PCF fabrication technologies [23] -[26] . Consequently, it is apparent that prior to fabrication of the proposed novel biosensor it is necessary to deployed sophisticated numerical techniques to analyse, optimise and perform simulation tests under various environmental conditions.

The article is structured as follows. In Section 1 is the introduction provided, then following this introduction, methodology is presented in Section 2, followed by numerical results and discussions provided in Section 2.1. The bend analysis of proposed PCF structure is reported in Section 2.2. Finally, conclusions are drawn in the last section.

2. Methodology

Using the finite element method (FEM), the cross-section of the PCF and the area containing the air holes is divided into homogeneous subspaces. In the FEM the subspaces are considered as triangle element to fit the circular shapes where Maxwell’s equations are solved. As boundary conditions, we use an anisotropic perfectly matched layer (PML) boundary condition, introduced by Guo, Y. et al. [18] . From Maxwell’s equations, the curl equation is given as:

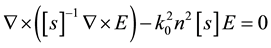(1)

where E presents the electric field vector, k₀ (=2π/λ) is the wave-number in the vacuum, n is the refractive index of the domain, where it is set to 1.45, [s] is the PML matrix, [s]^‒1 is an inverse matrix of [s] and λ is the operating wavelength. The dimensions of the computational window in x- and y-direction are; W_x = 100 μm and W_y = 80 μm, and the width of the PML, w is 2 μm.

Figure 1 shows the proposed PCF structure with five rings of air holes where, the radius of each is 2 µm, and the hole to hole spacing is set to 7 μm. The core region is composed of smaller air holes of a radius 1.5 µm surrounded by three concentric circles. The diameters of the circles are d₁ = 12 µm, d₂ = 16 µm, d₃ = 26 µm, d₄ = 30 µm, respectively. The refractive indices of region 1and region 3 are n₁ =1.5 and n₃= 1.501 and the refractive index of background is 1.45. While the refractive index, n₂ of region 2 represents the analyte to be detected.

2.1. Results and Discussion

The development of PCFs offers the prospect of superior fiber sensing for low refractive index materials such as liquids and gases. In particular, for sensing physical, chemical and biological characteristics of liquids and gases,

PCFs may offer unprecedented sensitivity since the material being sensed can be inserted into the fiber holes and experience long range interaction with guided light. Therefore, in this PCF biosensor, from the application point of view, we have examined a range of refractive indexes, in order to investigate the performance of the biosensor for various gas and liquid analyses. It is obvious that when the biosensor interacts with a certain known analytes, and in case if this analytes contains another unknown contaminant/substance then the refractive index will change to unknown refractive index, therefore, we have taken a range of refractive indexes (e.g. 1.0 - 1.38) in order to test the performance of the biosensor and improve its sensitivity.

Figure 2 shows the electric field profile in absence of the analyte, where n₂ is set to 1. It can be observed that the electric field is mainly concentrated in the PCF core and region 1. On the other hand, electric field is partly evanescent in region 2. Therefore, one may think to fill the region 2 various analytes and investigate the interaction between light and analytes.

Next, Figure 3 and Figure 4 illustrates the variation of the real part of the effective index Re (neff) with the operating wavelength, where n₂ is set to 1.38 and 1.33, respectively. At longer wavelengths, Re (neff) is low, while it increases with decreasing λ and reaches 1.38 at λ = 0.6 µm when n₂ is set to 1.38. Therefore, the sensitivity of the proposed PCF towards λ is expected to be high at λ = 0.6 µm. On the other hand, Figure 4 shows that the Re (neff) are higher than the refractive index of analyte (n₂ = 1.33), where this may be an evident of less sensitive structure.

Figure 5 shows that the confinement loss remains at around 0 dB/m for water when λ varies from 0.6 µm to 1.1 µm. However, when n₂ increases to 1.38, the confinement loss is negative and drops to −60 dB/m when λ is around 0.6 µm. This result shows that the sensor is suitable to detect analytes of refractive index of 1.38.

Next, sensitivity is one of the important issues regarding the practical development of sensor based optical fibers. To quantify the fiber efficiency as a gas or liquid sensor, the interaction between light and target analyte can be defined as [1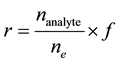2] :

(2)

where n_analyte is the refractive index of the analyte introduced into the cladding region, n_e is the effective refractive index of the guided mode and f the fraction of the total power located in the analyte region. For a particular fiber mode f can be calculated by integrating the optical power inside the analyte region and dividing it by the total power carried by that mode and expressed as [11] ;

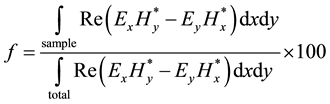(3)

where E_x/y is the electric field in the x or y direction and H_x/y is the magnetic field in the x or y direction.

The ratio f defines the percentage of energy present in the analyte region, where it is filled with various indexed analytes.

It can be seen from Figure 6 that the proposed PCF sensor is more sensitive to 1.38-indexed material than the 1.33. As expected, the sensitivity of the proposed PCF is at peak at λ = 0.6 µm. In addition, the sensitivity is increasing with decreasing wavelength for both indices. It is critical to investigate the effect of the thickness of the sensing region on the sensitivity of the proposed PCF sensor. The thickness is defined as (d₃ ‒ d₂)/2 where d₂ and d₃ are the diameter of region 2 and region 3, respectively. In this regard, Figure 7 shows the variation of the sensitivity with the thickness of the analyte region where n₂ is fixed to 1.38. It can be noticed that the sensitivity varies slowly when the thickness varies from 2 µm to 3.8 µm, whereas, it increases rapidly and reaches its maximum when the thickness exceeds 3.85 µm.

2.2. Bend Analysis

The propagation of light in PCFs is related to the existence of air hole rings around the core region. The air holes cause leakage of light from the core into the outer air holes region. The power leaks out of the core region at a bend and may be absorbed by its neighboring region. When the PCF is bent, a small percentage of the power is absorbed causing changes in the coating region that may be considered as a sensing region.

Due to leaky nature of the PCF, the bending effect is expected to be of high interest for optical sensors. The calculations of confinement losses and optical powers are based on the fact that the bend structure is circular where the perfect matched layers are placed along the radiation direction (x direction). The PCF with bend is replaced by a straight structure where the equivalent refractive index is given by this equation [27] .

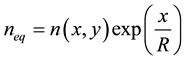(4)

where n(x, y) presents the refractive index of the straight PCF and R is the bend radius.

In order to investigate the effect of the bending on the performances of the proposed PCF sensor, the structure is bent. Bending the PCF makes modes leak out of the central core to interact with the surrounding region. However, due to the presence of air holes responsible of reflections, the guided mode slightly leaks out. To confirm that the electric field is calculated and reported in Figure 8 and Figure 9 (for simplicity, we present the first ring). It can be observed that the electric field in Figure 8 becomes more concentrated in the central region and tend to shift in the direction of the bend. By increasing the bending radius to R = 2 cm, a portion of the electric field is more confined to the center, which means that the field overlaps weakly with the analytes in the active region.

The next step investigates the sensitivity of the proposed sensor for various bending radii as a function of wavelength. The response of the sensor is shown in Figure 10 when the sensing region is filled with various analytes. The sensitivity defined as the maximum slope of the curves in Figure 10, shows a decrease when the bending radius increases from R = 1 cm to R = 2 cm. This is in agreement with the calculation of the electric

field shown in Figure 8 and Figure 9, also the bending loss increases; therefore a small fraction of the field reaches the sensing region, which results in poor overlap with analytes.

Finally, we believe that proposed PCF structure might be beneficial for several applications such as chemical and biological sensing of species such as those required in medical diagnostics and environmental contamination studies [11] [27] -[30] . Moreover, this indicates that applications such as biomedical diagnostics that involve detection of samples using water (n of the water ≈1.33) as a solvent is possible. For example, this fiber can be used in the study of complex systems like bacteria colonies where their size can be monitored using scatter measurements [30] .

3. Conclusion

A photonic crystal fibre (PCF) with a modified core used for environmental application sensing is designed. The proposed sensor is designed, optimized and tested for various environmental analytes, using versatile simulation technique. The proposed PCF sensor structure is unique due to its structure and its applications, in particular the sensing channels (regions) arrangements that enable simultaneously sensing of various multi-analytes that can be placed in the PCF engineered channels (regions 1, 2 and 3). This PCF sensor is highly sensitive and can be deployed for potential medical and environmental sensing applications using various gas and liquid analytes. The PCF sensing region is optimized to enhance the interaction between the light and analytes. Due to complex environmental/location applications, the bending of the PCF structure is scrutinized. It is shown that the bend structure based sensor is more sensitive to aqueous environment at short wavelength. It is found that the proposed sensor can detect gas and chemical species at long operating wavelength. This also shows an added value to the uniqueness of the proposed PCF sensor as it can be deployed also for short and long wavelength sensing applications.

References

NOTES

^*Corresponding author.