Optics and Photonics Journal
Vol.04 No.11(2014), Article ID:51666,6 pages
10.4236/opj.2014.411031
Nonlinear Ionization of Molecules by Intense Transform-Limited Gaussian Laser Pulses
Samira Barmaki, Salima Hennani, Marc-André Albert, Stéphane Laulan
Laboratoire de Physique Computationnelle et Photonique, Université de Moncton Campus de Shippagan, Shippagan, Canada
Email: samira.barmaki@umoncton.ca
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 25 August 2014; revised 21 September 2014; accepted 14 October 2014
ABSTRACT
We present in this paper an investigation of the nonlinear process of above-threshold ionization. The process arises when an atomic or molecular system, exposed to an intense laser pulse, conti- nues to absorb more photons than that needed for the ionization to occur. We trigger this non- linear process in a simple molecular system by exposing it to an intense transform-limited Gaus- sian laser pulse of 267-nm wavelength which is the third harmonic of an 800-nm wavelength Ti- sapphire laser. We explore the characteristics of the process by analyzing the kinetic-energy spectra of the electrons ejected from the molecular system under different laser peak intensities.
Keywords:
Nonlinear Ionization Process, Intense Femtosecond Laser Fields, Multiphoton Absorption in Molecular Continuum, Transform-Limited Gaussian Laser Pulse

1. Introduction
The recent progress in laser technology has made possible the generation of laser pulses that are increasingly shorter and intense [1] -[3] . Their characteristics and shape made them ideal tools to probe the ultrafast motion of electrons inside an atomic or a molecular system [4] [5] . Highly nonlinear processes arise when a system is exposed to such pulses. One of the most intriguing nonlinear processes discovered to date is the above-threshold ionization (ATI) process that was first observed by Agostini et al. in 1979, when they were experimentally investigating the irradiation of xenon gas with an intense laser field [6] . The measured kinetic-energy spectrum of the ejected electrons (ATI spectrum) from xenon atoms showed an unusual shape that consists of a series of regularly spaced peaks that are surprisingly separated by exactly the photon frequency of the incident laser field. Since then, more experimental studies have been launched on xenon and other rare gases (Kr, Ar, Ne) to explore the nonlinear process in greater detail [7] - [9] . These investigations have been accompanied by the launching of a series of theoretical studies that have supported the observations made by the experimentalists [10] - [12] . The findings of all these studies indicate that the ATI process shows quite clearly how an atomic or molecular system, under certain conditions, can successively absorb photons beyond the minimum necessary for the ionization to occur. Different features could appear in the ATI process depending of the characteristics and the shape of the incident laser pulses. In most of the conducted studies, the ATI process was successfully triggered and investigated using transform-limited laser pulses, i.e. unchirped pulses. However, few recent studies have pointed out the efficiency of chirped laser pulses as well in exploring and controlling the process [13] - [17] .
In this paper, we numerically investigate the ATI process in the hydrogen molecular ion  exposed to an intense transform-limited Gaussian laser pulse of 267-nm wavelength (photons of 4.65 eV), which corresponds to the third harmonic of an 800-nm wavelength Ti: sapphire laser. Our calculation of the whole electronic structure of the ion is based on a discretization technique using B-spline functions [18] [19] . This technique has proven its efficiency to accurately calculate the density of the continuum electronic states [20] . A realistic and precise representation of the electronic continuum is necessary to adequately describe the absorption of the molecular system of a number of excess photons beyond its ionization threshold which causes the appearance of the ATI process. Our treatment of the laser-ion interaction consists in solving the time-dependent Schrödinger equation (TDSE), describing the motion of the electron in the presence of the laser field. The approach we used to solve the TDSE is based on a spectral method that gives very accurate results and allows easy retrieval of the physical quantities of interest such as the ionization probability and the kinetic-energy spectra of the ejected electrons [15] - [17] . We accurately generate the ATI process under different laser peak intensities. We show how the increase of the laser intensity induces changes in the electronic structure of the ion which affects the shape of the emitted ATI spectra.
exposed to an intense transform-limited Gaussian laser pulse of 267-nm wavelength (photons of 4.65 eV), which corresponds to the third harmonic of an 800-nm wavelength Ti: sapphire laser. Our calculation of the whole electronic structure of the ion is based on a discretization technique using B-spline functions [18] [19] . This technique has proven its efficiency to accurately calculate the density of the continuum electronic states [20] . A realistic and precise representation of the electronic continuum is necessary to adequately describe the absorption of the molecular system of a number of excess photons beyond its ionization threshold which causes the appearance of the ATI process. Our treatment of the laser-ion interaction consists in solving the time-dependent Schrödinger equation (TDSE), describing the motion of the electron in the presence of the laser field. The approach we used to solve the TDSE is based on a spectral method that gives very accurate results and allows easy retrieval of the physical quantities of interest such as the ionization probability and the kinetic-energy spectra of the ejected electrons [15] - [17] . We accurately generate the ATI process under different laser peak intensities. We show how the increase of the laser intensity induces changes in the electronic structure of the ion which affects the shape of the emitted ATI spectra.
Atomic units (a.u.)  are used throughout the paper unless otherwise mentioned.
are used throughout the paper unless otherwise mentioned.
2. Laser-Ion Interaction Approach
In our investigation, the laser pulse is assumed to be linearly polarized along the  axis, with its vector potential given by:
axis, with its vector potential given by:
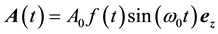 (1)
(1)
 is the peak amplitude, which is related to the laser central frequency
is the peak amplitude, which is related to the laser central frequency 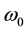 and the peak intensity
and the peak intensity  by:
by:
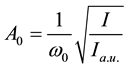 (2)
(2)
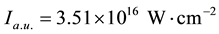 is the atomic unit of intensity.
is the atomic unit of intensity.
We consider the laser pulse having a Gaussian time envelope 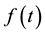 identical to that given in [21] [22] :
identical to that given in [21] [22] :
 (3)
(3)
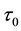 is the FWHM duration of the transform-limited pulse of frequency bandwidth:
is the FWHM duration of the transform-limited pulse of frequency bandwidth:
 (4)
(4)
The kinetic-energy spectrum of the ejected electrons, i.e. the ATI spectrum, is calculated by using the following expression:
 (5)
(5)
where 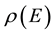 is the density of continuum states [20] and
is the density of continuum states [20] and 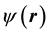 the electronic stationary wave function associated to the electronic state of energy
the electronic stationary wave function associated to the electronic state of energy

3. Results and Discussion
To trigger the nonlinear ATI process, we have exposed the hydrogen molecular ion to a transform-limited Gaussian laser pulse of photon frequency 




We show, in Figure 1(b), the ATI spectrum obtained at the end of the laser pulse interaction with the ion. The ATI spectrum exhibits a series of successive peaks localized around some specific electronic energies. All these peaks are the consequence of the excessive absorption of the ion of additional photons beyond the minimum of 7 needed for the ionization to occur. Here, the molecular ion absorbs more than 9 additional photons above its ionization threshold.
We also have exposed the molecular ion to a laser pulse of intensity 
Figure 1. (a) Variation of the laser pulse vector potential A(t) in time. The laser pulse has a central frequency ω0 = 0.171 a.u. (4.65 eV), peak intensity I = 1 × 1014 W∙cm−2, and FWHM duration τ0 = 120 a.u. (2.9 fsec); (b) ATI spectrum generated by the pulse.
creased later to



which is the average energy that the electron of the molecular ion acquires when it is submitted to the electric field.
Figure 3 indicates the changes that occur in the electronic structure of the ion depending of the magnitude of the laser intensity. When the pulse is of 

Figure 2. ATI spectra emitted from the molecular ion exposed to a laser pulse of photon frequency ω0 = 0.171 a.u (4.65 eV), FWHM duration τ0 = 120 a.u. (2.9 fsec) and for three different intensities: I = 1 × 1014 W∙cm−2, I = 2 × 1014 W∙cm−2 and I = 4 × 1014 W∙cm−2.
Figure 3. Electronic structure of the ion when submitted to a pulse of intensity (a) I = 1 × 1014 W∙cm−2; (b) I = 2 × 1014 W∙cm−2; and (c) I = 4 × 1014 W∙cm−2.






where 

Our numerical treatment of the laser pulse interaction with the molecular ion generates precise ATI spectra. The results, presented in Figure 2, accurately recreate the multiphoton absorption in the molecular continuum for three different laser peak intensities. They precisely indicate the kinetic energies 










4. Conclusions
We have investigated the nonlinear ATI process in the hydrogen molecular ion under a laser pulse of 267-nm wavelength. We have generated the ATI spectra under different laser peak intensities with a high degree of accuracy. The obtained spectra are characterized by a series of successive peaks separated exactly by the photon frequency of the incident laser pulse. We have explored the sensitivity of the process to the laser intensity. The more the intensity is increased, the more important the displacement of the ion electronic states becomes which affects the energy of the ejected electrons and then the shape of the ATI spectra.
Our study could be applicable to other simple molecular systems. The case of nonsymmetric molecules will
Figure 4. Schematic description of the nonlinear ATI process.
be interesting as we expect the ATI spectra emitted from these systems to be sensitive to the carrier-envelope phase of a short laser pulse. The appropriate adjustment of this laser parameter will be the key to control the nonlinear behavior of such systems under short and intense laser fields.
Acknowledgements
The present research was supported by the National Sciences and Engineering Research Council of Canada (NSERC) and by the New-Brunswick Innovation Foundation (NBIF). Allocation of CPU time and assistance with the computer facilities from the Atlantic Computational Excellence Network (ACEnet, St-John’s, NL, Canada) and from the “Réseau Québecois de Calcul de Haute Performance” (RQCHP, Sherbrooke, QC, Canada) are acknowledged.
References
- Diels, J.C. and Rudolph, W. (1996) Ultrashort Laser Pulse Phenomenon: Fundamentals, Techniques and Applications on Femtosecond Time Scale. Academic Press, New York.
- Agostini, P. and DiMauro, L.F. (2004) The Physics of Attosecond Light Pulses. Reports on Progress in Physics, 67, 813-855. http://dx.doi.org/10.1088/0034-4885/67/6/R01
- Yamanouchi, K. and Chin, S.L. (2007) Progress in Ultrafast Intense Laser Science III. Springler-Verlag, Berlin.
- Krausz, F. and Ivanov, M. (2009) Attosecond Physics. Review of Modern Physics, 81, 163. http://dx.doi.org/10.1103/RevModPhys.81.163
- Barmaki, S., Guessaf, K. and Laulan, S. (2011) Imaging of Ultrafast Electron Motion in Molecules. Canadian Journal of Physics, 89, 703-707. http://dx.doi.org/10.1139/p11-039
- Agostini, P., Fabre, F., Mainfray, G., Petite, G. and Rahman, N.K. (1979) Free-Free Transitions Following Six-Photon Ionization of Xenon Atoms. Physical Review Letters, 42, 1127. http://dx.doi.org/10.1103/PhysRevLett.42.1127
- Freeman, R.R., Bucksbaum, P.H., Milchberg, H., Darack, S., Schumacher, D. and Geusic, M.E. (1987) Above- Threshold Ionization with Subpicosecond Laser Pulses. Physical Review Letters, 59, 1092-1095. http://dx.doi.org/10.1103/PhysRevLett.59.1092
- Schafer, K.J., Yang, B.R., DiMauro, L.F. and Kulander, K.C. (1993) Abovethreshold Ionization beyond the High Harmonic Cutoff. Physical Review Letters, 70, 1599. http://dx.doi.org/10.1103/PhysRevLett.70.1599
- Paulus, G.G., Nicklich, W., Zacher, F., Lambropoulos, P. and Walther, H. (1996) High-Order Above-Threshold Ionization of the Atomic Hydrogen Using Intense, Ultrashort Laser Pulses. Journal of Physics B: Atomic, Molecular and Optical Physics, 29, L249-L256.
- Javanainen, J., Eberly, J.H. and Su, Q.C. (1988) Numerical Simulations of Multiphoton Ionization and Above-Thre- shold Electron Spectra. Physical Review A, 38, 3430. http://dx.doi.org/10.1103/PhysRevA.38.3430
- Cormier, E., Garzella, D., Breger, P., Agostini, P., Chériaux, G. and Leblanc, C. (2001) Above-Threshold Ionization Contrast and Channel Closure in Argon. Journal of Physics B: Atomic, Molecular and Optical Physics, 34, L9-L17.
- Becker, W., Grasbon, F., Kopold, R., Milosevic, D.B., Paulus, G.G. and Walther, H. (2002) Above-Threshold Ionization: From Classical Features to Quantum Effects. Advances in Atomic Molecular and Optical Physics, 48, 35-98. http://dx.doi.org/10.1016/S1049-250X(02)80006-4
- Xiang, Y., Niu, Y. and Gong, S. (2009) Above-Threshold Ionization by Few-Cycle Nonlinear Chirped Pulses. Physical Review A, 80, Article ID: 023423. http://dx.doi.org/10.1103/PhysRevA.80.023423
- Nakajima, T. (2007) Above-Threshold Ionization by Chirped Laser Pulses. Physical Review A, 75, Article ID: 053409. http://dx.doi.org/10.1103/PhysRevA.75.053409
- Laulan, S., Ba, H.S. and Barmaki, S. (2014) Excitation and Ionization of the Hydrogen Atom by Intense Femtosecond Chirped Laser Pulses. Canadian Journal of Physics, 92, 194-199. http://dx.doi.org/10.1139/cjp-2013-0389
- Laulan, S., Haché, J., Ba, H.S. and Barmaki, S. (2013) Ionization Process of Atoms by Intense Femtosecond Chirped Laser Pulses. Journal of Modern Physics, 4, 20-26. http://dx.doi.org/10.4236/jmp.2013.410A1002
- Barmaki, S., Ba, H.S. and Laulan, S. (2013) Control of the Atomic Ionization with Short and Intense Chirped Laser Pulses. Journal of Modern Physics, 4, 27-31. http://dx.doi.org/10.4236/jmp.2013.410A1003
- de Boor, C. (1978) A Practical Guide to Splines. Springer-Verlag, New York.
- Bachau, H., Cormier, E., Decleva, P., Hansen, J.E. and Martin, F. (2001) Applications of B-Splines in Atomic and Molecular Physics. Reports on Progress in Physics, 64, 1815-1943. http://dx.doi.org/10.1088/0034-4885/64/12/205
- Barmaki, S., Laulan, S., Bachau, H. and Ghalim, M. (2003) The Ionization of One-Electron Diatomic Molecules in Strong and Short Laser Fields. Journal of Physics B: Atomic, Molecular and Optical Physics, 36, 817-824. http://dx.doi.org/10.1088/0953-4075/36/5/303
- Lee, T.G., Pindzola, M.S. and Robicheaux, F. (2009) Energy and Angular Differential Probabilities for Photoionization of He Using Chirped Attosecond Soft X-Ray Pulses. Physical Review A, 79, Article ID: 053420. http://dx.doi.org/10.1103/PhysRevA.79.053420
- Saleh, B.E.A. and Teich, M.C. (2007) Fundamentals of Photonics. John Wiley and Sons Inc., Hoboken.





