Optics and Photonics Journal
Vol.4 No.4(2014), Article ID:45520,7 pages DOI:10.4236/opj.2014.44009
Numerical Calculation of Seawater Temperature Sensing Based on Polydimethylsiloxane-Coated Microfiber Knot Resonator
Hongjuan Yang1, Shanshan Wang1, Kening Mao1,2, Guoxiang Li1, Jing Wang1
1Institution of Information Science and Engineering, Ocean University of China, Qingdao, China
2Department of Optical Engineering, Zhejiang University, Hangzhou, China
Email: wjing@ouc.edu.cn
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 16 January 2014; revised 18 February 2014; accepted 14 March 2014
ABSTRACT
A seawater temperature sensing method based on polydimethylsiloxane-coated (PDMS-coated) microfiber knot resonator (MKR) is proposed, which has the advantages of high sensitivity and weak salinity dependence. The dependences of the temperature sensitivity on fiber diameter, coating thickness and probing wavelength are theoretically investigated and the range of coating thickness for weak salinity dependence is obtained. By optimizing the parameters of the seawater temperature sensing system, when the probing wavelength is 1550 nm, the fiber diameter is 1 μm, and the coating thickness is 5 μm, the sensitivity can reach to 0.197 nm/˚C. Results shown here are beneficial to find the optimal parameters for the temperature sensors with high sensitivity and weak salinity dependence.
Keywords:Seawater Temperature, Sensor, Microfiber Knot Resonators, Coating

1. Introduction
Seawater temperature is one of the most important parameters of the ocean detection, which is important in oceanography, meteorology, biology, and marine military. Several seawater temperature detection methods have been reported, including conductivity-temperature-depth (CTD) system, microwave remote sensing and sensors based on fiber bragg grating [1] -[3] . The CTD system product is mature, which is based on electrical sensing, but too expensive. Microwave remote sensing can only detect the skin temperature of seawater. Compared to the other methods, optical sensing has the advantages of fast response, free of insulation and immunity to electromagnetic interference, and the sensor based on fiber Bragg grating has a sensitivity of 0.01 nm/˚C.
In recent year, microfiber resonator (MR) has attracted more and more attention because of fast response, compact size, low loss and high sensitivity. The MRs can be used as refractive index, salinity, and temperature sensors, which have been demonstrated successfully and show high sensitivity [4] -[12] . Yu Wu et al. reported the temperature sensors based on silica and polymer MKRs, which have the sensitivities of 0.052 nm/˚C and 0.266 nm/˚C, respectively. Xu Zeng et al. proposed a temperature sensor based on polymer-coated MKR, which has the sensitivity of 0.27 nm/˚C. These MKRs detecting temperature are put on the heating platen and detect the temperature of solid. We can conclude that the temperature sensitivity of the polymer-coated MKRs is higher than that of the silica MKRs. To our knowledge, seawater temperature sensing based on polymer-coated microfiber knot resonator has not been reported yet.
In this paper, we propose a temperature sensor based on polydimethylsiloxane-coated microfiber knot resonator with high sensitivity and weak salinity dependence. The dependences of the sensitivity on fiber diameter, coating thickness and probing wavelength are theoretically investigated and the range of coating thickness for weak salinity dependence is obtained. Results shown here may offer helpful references for assembling micro-photon-ics device used in seawater temperature sensing and detection.
2. Theory Model
The schematic diagram of the seawater temperature sensor based on PDMS-coated microfiber knot resonator is shown in Figure 1. The symbol d is the fiber diameter, and t is the coating thickness. The MKR is fabricated using a PDMS-coated microfiber by a knotted way. The microfiber and the single model fiber are connected with a taper.
The polymer PDMS is chosen because the thermo-optical coefficients of the PDMS is negative and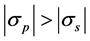 . σp = −1.8 × 10−4/˚C [13] , σs = −1.0 × 10−4/˚C [14] and σf = 1.14 × 10−5/˚C [15] are the thermo-optical coefficients of the PDMS, seawater and the microfiber, respectively. The MKRs can be used in temperature sensing because of the thermo-optical effect and thermal-expanding effect. Compared to the thermo-optical effect, the thermal-expanding effect can be ignored.
. σp = −1.8 × 10−4/˚C [13] , σs = −1.0 × 10−4/˚C [14] and σf = 1.14 × 10−5/˚C [15] are the thermo-optical coefficients of the PDMS, seawater and the microfiber, respectively. The MKRs can be used in temperature sensing because of the thermo-optical effect and thermal-expanding effect. Compared to the thermo-optical effect, the thermal-expanding effect can be ignored.
The temperature can influence the refractive indices of the seawater and the material, then the effective refractive index (neff). The neff can be written as neff ≈ n1η1+ n2η3+ n3η3 [14] . The n1, n2, n3 are the refractive indices of the silica, PDMS and seawater, respectively. The η1, η2, η3 are the fractional power transmitted in the silica, PDMS, and seawater, respectively. Since the refractive index of the seawater is the function of temperature, salinity and probing wavelength [14] , temperature and salinity both influence the neff. It is necessary to remove the influence of the salinity to detect the temperature accurately. In this paper, the coating method is proposed.
The sensitivity of the sensor is defined as the shift of resonance wavelength to the change of the temperature, which can be defined as
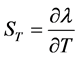 (1)
(1)
where T is the seawater temperature, 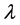 is resonance wavelength, and can be written as
is resonance wavelength, and can be written as 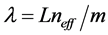 [16] . Actually, the change of temperature influence the neff first, then the shift of the resonance wavelength. Thus, Equation (1) can be written as
[16] . Actually, the change of temperature influence the neff first, then the shift of the resonance wavelength. Thus, Equation (1) can be written as
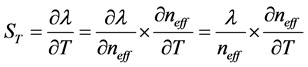 (2)
(2)
It can be seen that the neff should be calculated first to obtain the sensitivity.
Using the finite element method, the neff is calculated by COMSOL, and the sensitivity is calculated by MATLAB. Since the neff is related to the probing wavelength, fiber diameter and coating thickness. We study the dependences of the sensitivity on these three parameters in next section.
3. Numerical Calculation and Discussion
3.1. The Influence of Salinity on Temperature Sensing
Similar to the temperature sensitivity, the salinity sensitivity can be described as [12] .
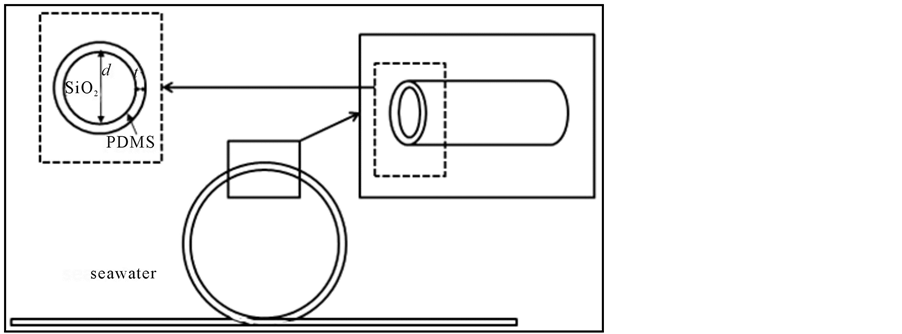
Figure 1. The schematic diagram of the seawater temperature sensor based on the microfiber knot resonator.
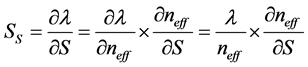 (3)
(3)
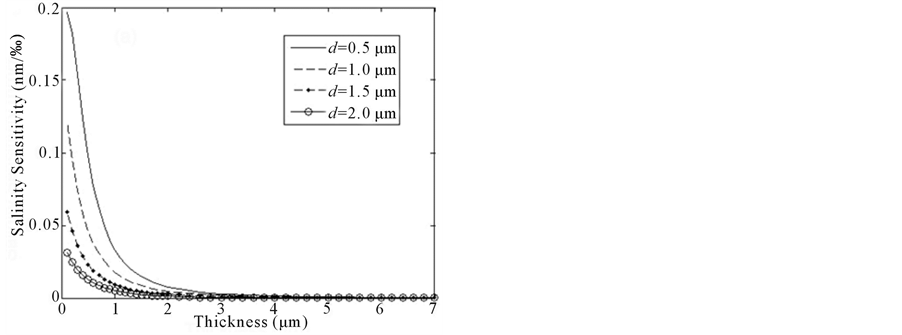
The dependence of salinity sensitivity on coating thickness is shown in Figure 2. We assume that the probing wavelength is 1550 nm, the fiber diameters are 0.5, 1.0, 1.5 and 2.0 μm, respectively in Figure 2(a). It can be seen that the salinity sensitivity decreases with the increasing coating thickness. When the coating thickness is very small, salinity sensitivity decreases sharply with the increasing coating thickness. When the coating thickness is up to 1μm and the fiber diameter is up to 1μm, the salinity sensitivity decreases to 0.018 nm/‰. With the increasing coating thickness, the salinity sensitivity decreases slowly and until closes to zero. In addition, we calculate the dependence of the salinity sensitivity on coating thickness at different probing wavelength in Figure 2(b). The probing wavelengths are assumed to be 660, 1064, 1310 and 1550 nm, respectively. It can be seen that when the coating thickness is 3 μm, the salinity sensitivity is already very low; when the coating thickness is 5 μm, the salinity sensitivity is closed to zero. Thus, we choose the range of coating thicknesses for weak salinity dependence is 3 - 5 μm. That is to say, when the coating thickness is between 3 to 5 μm, the influence of salinity on temperature detection can be ignored.
After coating, the most power transmits in the polymer, and little in the seawater. With the increasing coating thickness, the power in seawater decreases gradually, and the contribution of seawater refractive index to the neff decreases gradually. And the salinity only influences the refractive index of seawater, not the PDMS’s. Thus, with the increasing coating thickness, the power in seawater decreases. Since salinity changes do little to neff, the resonance wavelength can be regarded as no change. So, the coated MKR can detect the seawater temperature without the influence of salinity.
3.2. The Temperature Sensitivity of Bared and Coated Microfiber
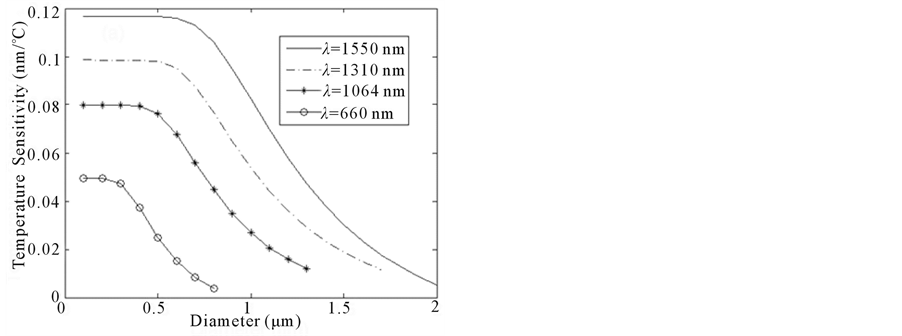
First, we calculate the temperature sensitivity before and after coating. Figure 3(a) shows that the dependence of the temperature sensitivity on fiber diameter of bared microfiber. The probing wavelengths are assumed to be 660, 1064, 1310 and 1550 nm, respectively. As is shown, the temperature sensitivity decreases with the increasing fiber diameter and the decreasing probing wavelength. The maximum value closes to 0.12 nm/˚C. Figure 3(b) shows that the dependence of the temperature sensitivity on fiber diameter of coated microfiber. The fiber diameter is assumed to be 1 μm. The temperature sensitivity dependences on fiber diameter of coated microfiber shows similar trend as the bared microfiber that increasing with the decreasing fiber diameter and the increasing probing wavelength. The highest sensitivity is about 0.18 nm/˚C, which is higher than that of the bared microfiber. We can conclude that the more power transmitted in polymer and seawater, the higher the sensitivity at the same probing wavelength.
Because of the thermo-optical coefficient of the silica and the seawater, the bared microfiber can be used in seawater temperature sensing. When the fiber diameter is small, the power mostly transmits in the seawater due to the evanescent field. So the refractive index of seawater has a large influence on the neff. The refractive
 (a)
(a) 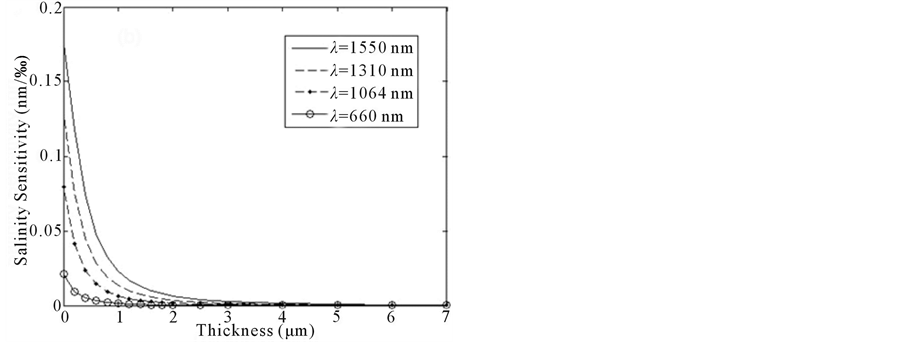 (b)
(b)
Figure 2 . The dependence of the salinity sensitivity on the coating thickness, (a) at different fiber diameter, (b) at different probing wavelength.
 (a)
(a) 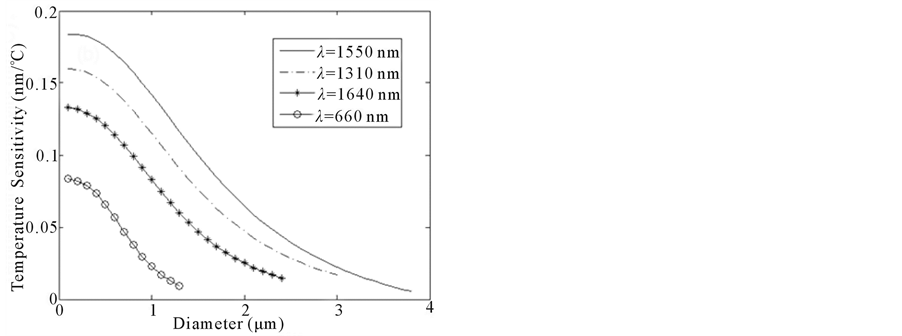 (b)
(b)
Figure 3. The dependence of the temperature sensitivity on the fiber diameter (a) before and (b) after coating.
index of seawater decreases with the increasing temperature. For this reason, to increase the sensitivity, the influence of the negative thermo-optical coefficient should be increased. So, we choose the polymer (PDMS) with a negative thermo-optical coefficient and its absolute value is larger than that of seawater.
3.3. The Dependence of the Temperature Sensitivity on the Fiber Diameter
As mentioned above, when the coating thickness ranges from 3 to 5 μm, the influence of salinity to temperature detection can be ignored. So we investigate the temperature sensitivity when coating thicknesses range from 3 to 5 μm. Figure 4(a) shows the dependence of the sensitivity on the fiber diameter, when t is 0, 3 and 5 μm. Results show that the temperature sensitivity decreases with the increasing fiber diameter at different coating thicknesses. The larger the coating thickness is, the higher the sensitivity. Figure 4(b) shows that the dependence of the temperature sensitivity on the fiber diameter at different probing wavelengths. The coating thickness is 5 μm. It can be seen that the temperature sensitivity dependences on the fiber diameter are same at different probing wavelength, and the temperature sensitivity increases with the increasing probing wavelength.
3.4. The Dependence of the Temperature Sensitivity on the Coating Thickness
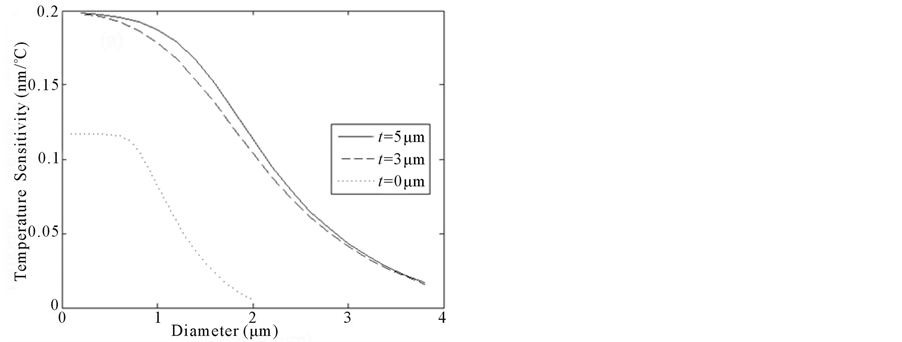
Above simulations indicate that coating can increase the temperature sensitivity. To find the optimal coating thickness is the next problem. Since the temperature sensitivity increases with the increasing probing wavelength, the probing wavelength is chosen to be 1550 nm. Figure 5 shows the dependence of the temperature sensitivity on the coating thickness at different fiber diameter. It can be seen that the temperature sensitivity increases with the increasing coating thickness and decreasing fiber diameter. When t ranges from 0 to 3 μm, the sensitivity increases sharply, and when t > 3 μm, the sensitivity increases slowly.
3.5. The Dependence of the Temperature Sensitivity on the Probing Wavelength
Besides the fiber diameter and coating thickness, the probing wavelength also influences the temperature sensitivity. As shown in Figures 3(b) and Figures 4(b), the temperature sensitivity increases with the increasing probing wavelength. Figure 6 shows the dependence of the temperature sensitivity on the probing wavelength. The fiber diameter is 1 μm, and the coating thickness is 5 μm. Results show that the sensitivity increases with the increasing probing wavelength. Thus, the large wavelength should be chosen in the experiments.
3.6. Parameters Design for Seawater Temperature Sensor
Combine the above results, the parameters for seawater temperature sensor can be chosen. Considering the loss and high sensitivity, the probing wavelength is assumed to be 1550 nm. When coating thickness ranges from 3 to 5 μm, the influence of the salinity on temperature detection can be ignored. The 5 μm coating thickness can meet the demand. Since the temperature sensitivity increases with the decreasing fiber diameter, the fiber di-
 (a)
(a) 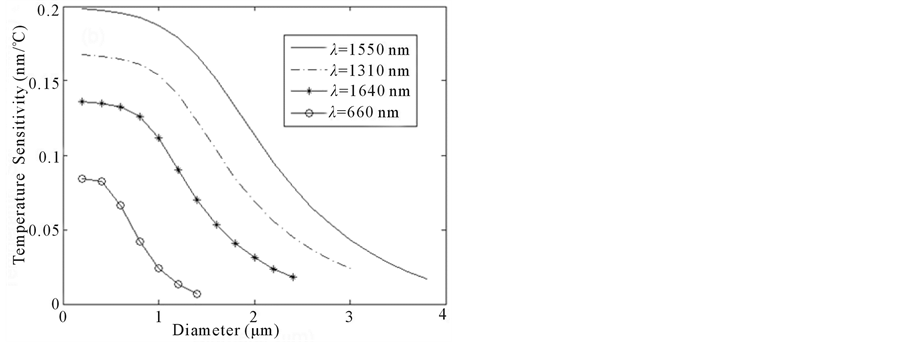 (b)
(b)
Figure 4. The dependence of the temperature sensitivity on the fiber diameter (a) λ = 1550 nm, at different coating thickness, (b) t = 5 μm, at different probing wavelength.
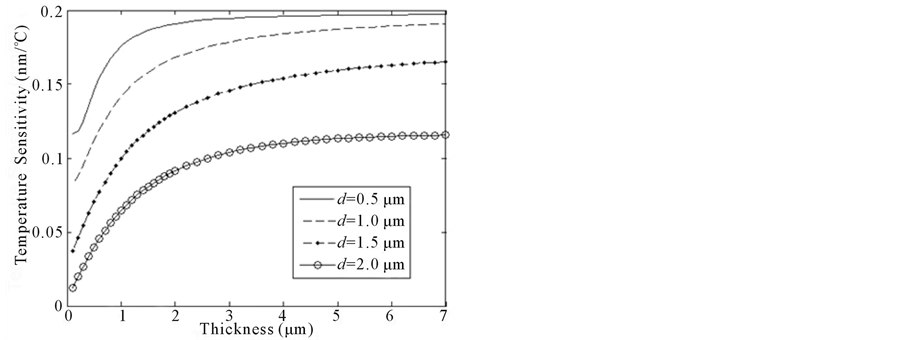
Figure 5. The dependence of the temperature sensitivity on the coating thickness.
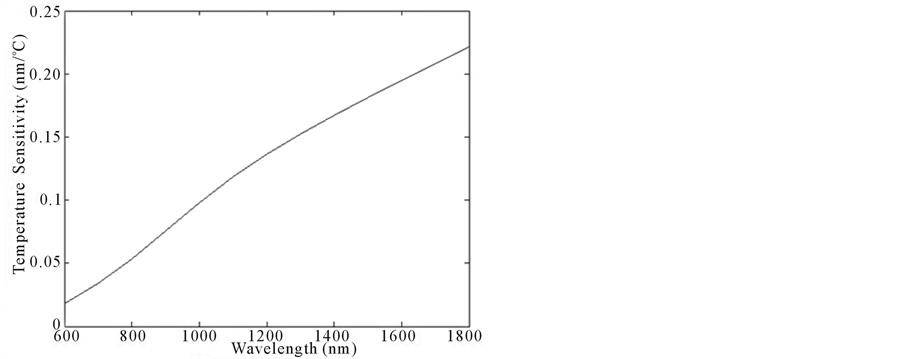
Figure 6. The dependence of the temperature on the probing wavelength.
ameter should be small. Considering the problem of drawing microfiber, the fiber diameter is chosen to be 1 μm. Thus, the parameters of the sensor are wavelength 1550 nm, fiber diameter 1 μm, the coating thickness 5 μm, and the calculated sensitivity is 0.197 nm/˚C.
4. Conclusion
In conclusion, we propose a temperature sensor based on polydimethylsiloxane-coated microfiber knot resonator with high sensitivity and weak salinity dependence. The dependences of the sensitivity on fiber diameter, coating thickness and probing wavelength are theoretically investigated and the range of coating thickness for weak salinity dependence is obtained. When coating thickness ranges from 3 to 5 μm, the influence of the salinity on temperature detection can be ignored. So the range of coating thickness for weak salinity dependence is 3 - 5 μm. The temperature sensitivity increases with the decreasing fiber diameter, the increasing coating thickness and the increasing probing wavelength. The most important thing is that the polymer should have a negative thermooptical coefficient and its absolute value is larger than that of seawater. To obtain a high sensitivity, large probing wavelength, small fiber diameter and large coating thickness should be chosen. By optimizing the parameters of the seawater temperature sensing system, when the probing wavelength is 1550 nm, the fiber diameter is 1 μm, and the coating thickness is 5μm, the sensitivity can reach to 0.197 nm/˚C. Results shown here are beneficial to find the optimal parameters for the temperature sensors with high sensitivity and weak salinity dependence, and offer helpful references for assembling micro-photonics device used in seawater temperature sensing and detection.
Acknowledgements
We would like to thank financial supports from the Natural Science Foundation of China (No. 61171161) and the Fundamental Research Project of Qingdao (No. 12-1-4-1-(26)-jch).
References
- Millard, R., Toole, J. and Swartz, M. (1980) A Fast Responding Temperature Measurement System for CTD Applications. Ocean Engineering, 7, 413-427. http://dx.doi.org/10.1016/0029-8018(80)90007-4
- Swift, C.T. (1980) Passive Microwave Remote Sensing of the Ocean—A Review. Boundary-Layer Meteorology, 18, 25-54. http://dx.doi.org/10.1007/BF00117909
- Pereira, D.A. and Fraza, O. (2004) Fiber Bragg Grating Sensing System for Simultaneous Measurement of Salinity and Temperature. Optical Engineering, 43, 299-304. http://dx.doi.org/10.1117/1.1637903
- Xu, F., Horak, P. and Brambilla, G. (2007) Optical Microfiber Coil Resonator Refractometric Sensor. Optics Express, 15, 7888-7893. http://dx.doi.org/10.1364/OE.15.007888
- Xu, F., Pruneri, V., Finazzi, V. and Brambilla, G. (2008) An Embedded Optical Nanowire Loop Resonator Refractometric Sensor. Optics Express, 16, 1062-1067. http://dx.doi.org/10.1364/OE.16.001062
- Guo, X. and Tong, L.M. (2008) Supported Microfiber Loops for Optical Sensing. Optics Express, 16, 14429-14434. http://dx.doi.org/10.1364/OE.16.014429
- Xu, F. and Brambilla, G. (2008) Demonstration of a Refractometric Sensor Based on Optical Microfiber Resonator. Applied Physics Letters, 92, 101126. http://dx.doi.org/10.1063/1.2898211
- Wu, Y., Rao, Y.J., Chen, Y.H. and Gong, Y. (2009) Miniature Fiber-Optic Temperature Sensors Based on Silica/Polymer Microfiber Knot Resonators. Optics Express, 17, 18142-18147. http://dx.doi.org/10.1364/OE.17.018142
- Zeng, X., Wu, Y., Hou, C.L., Bai, J. and Yang, G.G. (2009) A Temperature Sensor Based on Optical Microfiber Knot Resonator. Optics Communications, 282, 3817-3819. http://dx.doi.org/10.1016/j.optcom.2009.05.079
- Chen, Y., Xu, F. and Lu, Y.Q. (2011) Teflon-Coated Microfiber Resonator with Weak Temperature Dependence. Optics Express, 19, 22923-22928. http://dx.doi.org/10.1364/OE.19.022923
- Wu, Y., Jia, L., Zhang, T.H., Jing, Y.J. and Gong, Y. (2012) Microscopic Multi-point Temperature Sensing Based on Microfiber Double-Knot Resonators. Optics Communications, 285, 2218-2222. http://dx.doi.org/10.1016/j.optcom.2011.12.107
- Wang, S.S., Wang, J., Li, G.X. and Tong, L.M. (2012) Modeling Optical Micro-Fiber Loops for Seawater Sensing. Applied Optics, 51, 3017-3023. http://dx.doi.org/10.1364/AO.51.003017
- Li, B.B., Wang, Q.Y., Xiao, Y.F., Jiang, X.F., Li, Y., Xiao, L. and Gong, Q. (2010) On Chip, High-Sensitivity Thermal Sensor Based on High-Q Polydimethylsiloxane-Coated Microresonator. Applied Physics Letters, 96, 251109. http://dx.doi.org/10.1063/1.3457444
- Quan, X.H. and Fry, E.S. (1995) Empirical Equation for the Index of Refraction of Seawater. Applied Optics, 34, 3477-3480.
- Klocek, P. (1991) Handbook of Infrared Optical Materials. Marcel Dekker, New York.
- Chao, C.Y. and Guo, L.J. (2006) Design and Optimization of Microring Resonators in Biochemical Sensing Applications. Journal of Lightwave Technology, 24, 1395-1402. http://dx.doi.org/10.1109/JLT.2005.863333

