Optics and Photonics Journal
Vol.3 No.8A(2013), Article ID:40627,12 pages DOI:10.4236/opj.2013.38A001
First Order Phase Transitions as Radiation Processes
Shanghai CEC Zhenhua Crystal Technology Co. Ltd., Shanghai, China
Email: *vitali.tatartchenko@orange.fr
Copyright © 2013 Vitali A. Tatartchenko et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received September 22, 2013; revised October 25, 2013; accepted November 21, 2013
Keywords: Peta Effect; First Order Phase Transitions; Vapour Condensation; Vapour Deposition; Melt Crystallization; Infrared Radiation; Atmospheric Phenomena
ABSTRACT
This paper presents new experimental evidence of the PeTa effect—infrared characteristic radiation under first order phase transitions, especially the crystallization of melts and the deposition and condensation of vapours/gases. The PeTa effect describes the transient radiation that a particle (i.e., atom, molecule or/and cluster) emits transient radiation during a transition from a meta-stable higher energetic level (in a super-cooled melt or a super-saturated vapour) to the stable condensed lower level (in a crystal or a liquid). The radiation removes latent heat with photons of characteristic frequencies that are generated under this transition. The abbreviation “PeTa effect” means Perel’man-Tatartchenko’s effect.
1. Introduction
This paper, presents experimental evidence for a new physical phenomenon—infrared characteristic radiation (IRCR)1 under first order phase transitions, especially the crystallization of melts and the deposition and condensation of vapours/gases. The effect was theoretically predicted by M. Perel’man [1] and was investigated by V. Tatartchenko for several alkali halides [2,3] and for sapphire [4]. In 2010, M. Perel’man deceased. In memory of Prof. Perel’man and to simplify the title “IRCR under first order phase transitions”, the term “PeTa (Perel’manTatartchenko’s) effect” is used in this paper as it has been used previously [5,6].
The basis of the PeTa effect is that a particle (i.e., atom, molecule or/and cluster) emits transient radiation during the transition from a meta-stable higher energetic level (in a super-cooled melt or a super-saturated vapour) to a stable and condensed lower level (in a crystal or a melt). The radiation removes the latent heat by photons with characteristic frequencies that are generated under this transition. The previous papers [1-16] present experimental and theoretical evidence for the PeTa effect, but as underscored in the discussion in [5], additional investigations concerning atmospheric phenomena are needed. In this paper, another striking demonstration of the PeTa effect is presented—infrared radiation during the deposition and condensation of air components at the temperature of liquid nitrogen. The experiments consist of a very simple scheme of deep cooling atmospheric air while recording the emissive spectra using an IR Fourier Spectrometer with a very sensitive MCT detector. The experiments allow estimation of both the range and the order of intensity of the PeTa radiation. The results can be used for crystal growth regulation [9], optics [11] and atmospheric sciences [12-16].
2. Experiment
2.1. Equipment
For the experiments, we used a PerkinElmer Frontier MIR spectrometer with a DynaScan interferometer, cooled with a liquid nitrogen MCT detector, and sealed and desiccated Ge-coated KBr optics, which enabled a scan range of Δλ = (1.2 - 28) µm while delivering ΔS = 0.4 cm−1 resolution and 15,000/1 pk-pk noise for 5 s scan. The regimes of function sb and cont are possible. For comparison, our similar experiments [2-4] with alkali halides and sapphire were carried out 35 years ago for the range Δλ = (1.2 - 7.0) µm under 3 different conditions: “low-resolution” spectra (Spectrometer IKS-21, optical resolution ΔS = 210 cm−1), “medium-resolution” spectra (Spectrometer IKS-21, ΔS = 90 cm−1), and “high-resolution” spectra (Spectrometer Specord-75 IR, ΔS = 5 cm−1). The scanning time for the range 1.2 - 7.0 µm was approximately 30 s. Thus, the resolution of our new device exceeds the highest resolution of our previous model by a factor of ten, and 2 - 3 s (an order of magnitude improvement over our previous experiments) is sufficient for the accumulation of data for one spectrum.
An irradiative object, a 200 ml aluminium cup, was placed approximately 4 cm from the input window of the spectrometer (Figure 1).
2.2. Experimental Procedure
A time of 0.58 s was chosen for the accumulation of data for one spectrum, and an average of 4 spectra were used. Thus, we could have a new spectrum every 2.32 s with a resolution of 4 cm−1. The temperature of the laboratory was 24˚C (297 K), the relative humidity supported at 32% (corresponding to 279 K for the water vapour dew point). Under these conditions, the integral radiation intensity U1 within the range of 1.2 - 22.5 µm was continuously recorded (Figure 2) from the wall of the irradiative cup (Figure 1). The first (background) Plank’s radiation spectrum, corresponding to room temperature (the time 289.6 s, i.e., point a1 of Figure 2), from the wall of the empty cup is presented in Figure 3 (curve a1). The spectrum has several absorption bands. It is well known that spectral peculiarities near 15 µm are associated with atmospheric CO2. The 7 - 14 µm range is the window for the atmospheric transparency; it generally does not contain any bands. In our case, the nature of the recorded absorption bands depended on the cup material and the air purity, but the bands did not influence the experimental results.
Several seconds after beginning our measurements, a similar cup with liquid nitrogen was placed inside of the first cup (Figure 2, point a1). The integral intensity of the radiation immediately decreased (Figure 2, the time between points a1 and b1) as a result of the temperature decreasing to 77 K. Ice (evidently H2O and most likely CO2) appeared on the cup wall and the integral intensity of the radiation increased (Figure 2, the range between points b1 and d1). The 6 consecutive spectra corresponding to the indicated time points (Figure 4) show a transformation of the irradiative spectra during this period (approximately 11 minutes) as the surface density of ice grains on the cup wall visibly increased. We explain the intensive IR radiation in this range as the PeTa effect during deposition of H2O and CO2 as well as the condensation of Ar and O2 (of the air components) on the cup wall. We hypothesize that the continuous augmentation of the integral intensity of the

Figure 1. Experimental facility.
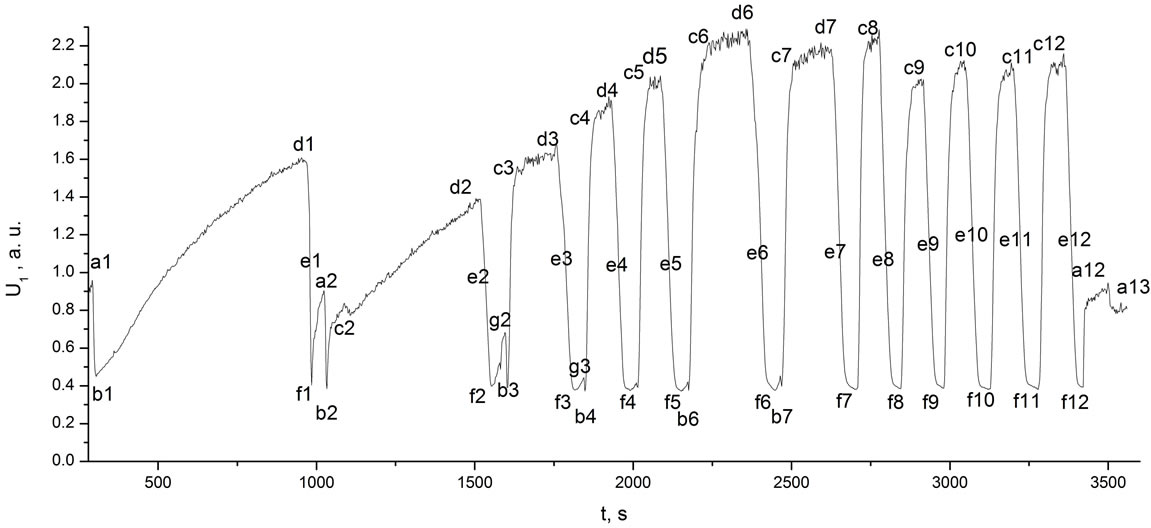
Figure 2. Integral intensity of the IR radiation U1 a.u. (arbitrary units) between 1.2 and 22.5 µm from the Al cup vs. experiment time.
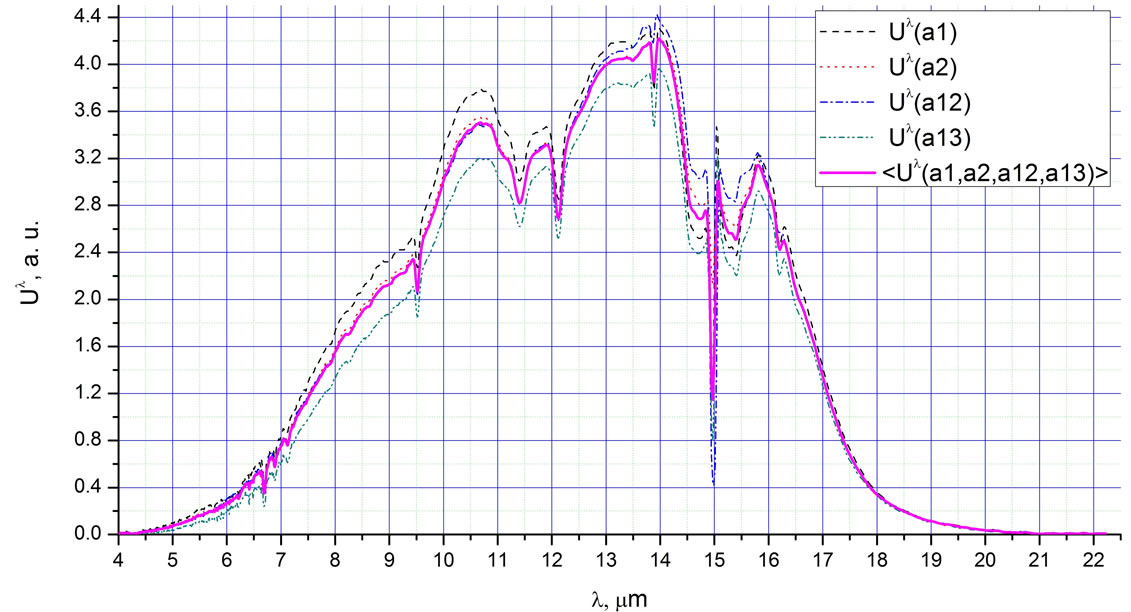
Figure 3. The four radiation spectra Uλ corresponding to room temperature at four time points of the experiment and their average.
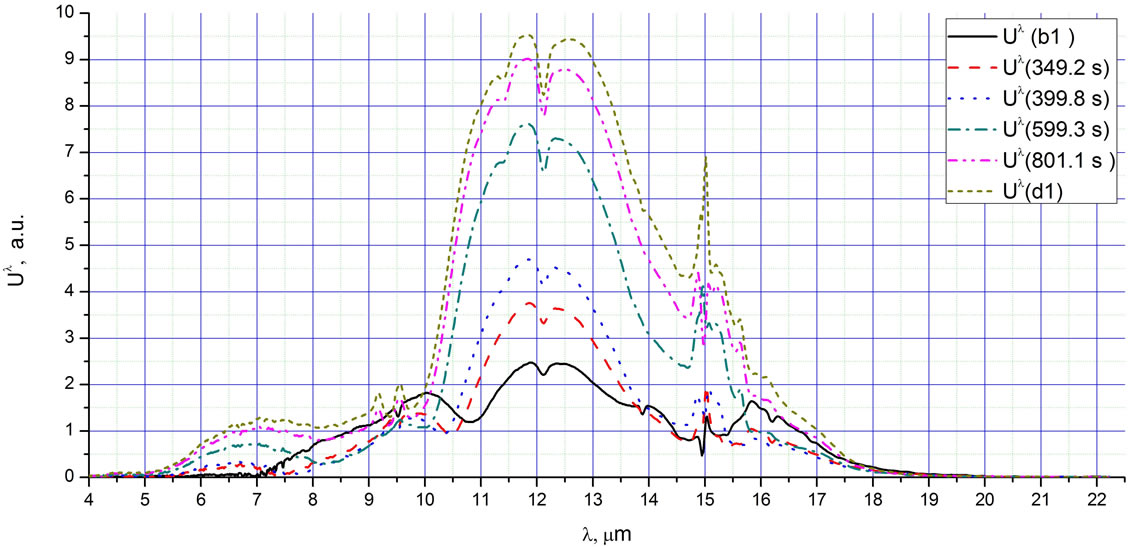
Figure 4. The six radiation spectra Uλ as the integral radiation intensity increases between times b1 and d1.
radiation during this time is connected with the increasing speed of deposition as well as the condensation of gases and water vapour on the cup wall because of the visibly increasing density of nucleation centres. Indeed, the polished surface of an aluminium cup is non-wetted by the water, thus it is difficult for nucleation centres to appear on it.
To verify this hypothesis, the following experiments were carried out. At point d1 (Figure 2), the internal cup containing liquid nitrogen (77 K) was replaced by a similar cup containing room temperature water (297 K). The intensity of radiation immediately decreased (e1 range on the Figure 2) to the level corresponding to the Plank’s radiation for the temperature of ice melting 273 K (point f1). We observed that after the ice thawed, the cup surface was covered with liquid drops. The radiation intensity began to increase up to point a2, which corresponds to the Plank’s intensity at a room temperature of 297 K (the a2 spectrum of the Figure 3). During this time, the water from the cup wall was partially evaporated. At point a2, the cup containing water was replaced by the cup containing liquid nitrogen (77 K). Here, the system repeated its behaviour at point a1, but the intensity level corresponding to point c2 was achieved much more rapidly because of the presence of the nucleation centres.
We repeated the procedure at point d2, but the duration of time for the water to heat the cup was shorter. In this case, the ice only thawed without water evaporation and the high radiation intensity of point c3 was achieved more quickly. At point d3, we removed the internal cup containing liquid nitrogen for a short time to allow the ice to melt. The high radiation intensity at point c4 was quickly achieved. We repeated the last procedure 10 times up to point a12 without waiting for the ice to melt completely. At point d6, the entire surface of the cup was covered with ice, after which we observed neither the formation of new nucleation centres nor increases in radiation intensity. The small decrease in the radiation intensity is most likely explained by the thickening of the ice layer and the decreasing of thermo-conductivity with respect to the classical Stephan’s problem. Thus, we can see the first confirmation of our hypothesis: in these conditions, the radiation intensity depends on the density and the sizes of the nucleation centres. To confirm that the spectrometer worked well, we periodically compared the background spectra. These four spectra and their average are presented in Figure 3 for the beginning (point a1 from the Figure 2), middle (point a2) and end (points a12 and a13) of the experiment.
At the first stage of our experiments, a scanning range of 1.2 - 22.5 µm was used, but we found that beyond the 4 - 22 µm range, there are no signals that exceed the noise. Figure 5 demonstrates this point within the 1.2 - 3.2 µm range. Thus, using the 4 - 22 µm range is sufficient for our experiments.
There are additional peculiarities of the obtained spectra that warrant further analysis. Figure 6 demonstrates four consecutive spectra between points c2 and d6 as the PeTa radiation intensity increased (bear in mind that the deposition in this range was interrupted several times with the removal of the cooling cup containing liquid nitrogen). We observed that between 1500 and 1650 s, after the ice first began to melt and without the additional heat provided by the room temperature water, the peak at 12.2 µm moved to 13 µm and the peak at 9.2 µm began to grow. In Figure 6, red lines represent the peak before the change and black lines represent the peak after the change. During the relatively stable stages of the radiation (points c7 - c12), the spectra were virtually unchanged.
The second confirmation of our hypothesis concerning the nature of the recorded IR radiation was obtained with the following experiment. The aluminium cup was replaced by a plastic cup. The cup was wetted with water, which formed a thin film across the entire external surface of the cup, and we repeated the previous procedure of inserting and removing the second cup containing liquid nitrogen. The growing ice layer covered the entire cup surface immediately after the first cooling. The integral intensity of the IR radiation achieved its maximum value and did not change during the experiment (Figure 7).
3. Previous Research
Data from the literature concerning the appearance of IR radiation during water phase transitions may be summarised as follows:
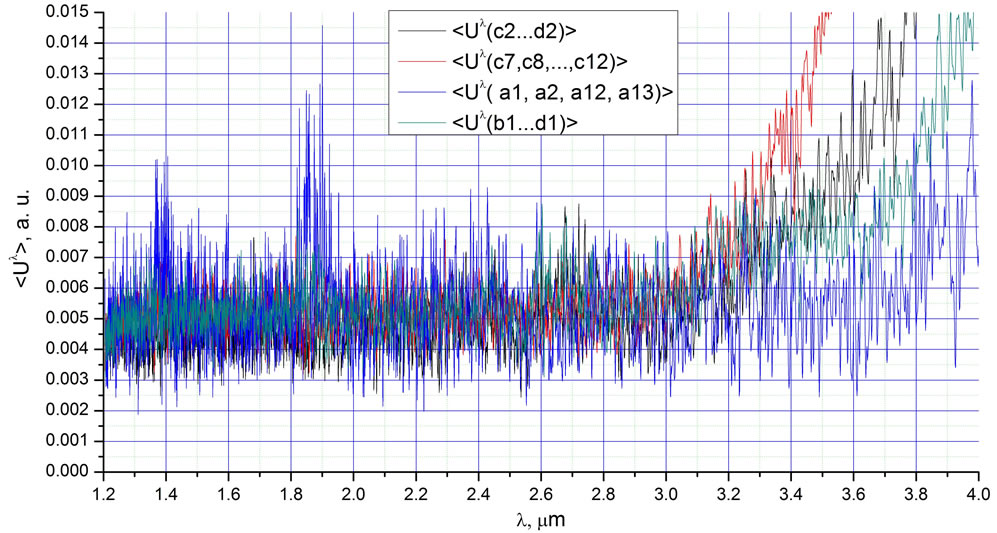
Figure 5. The four average radiation spectra Uλ in the range 1.2 - 4.0 µm. Variables are labelled on the figure.
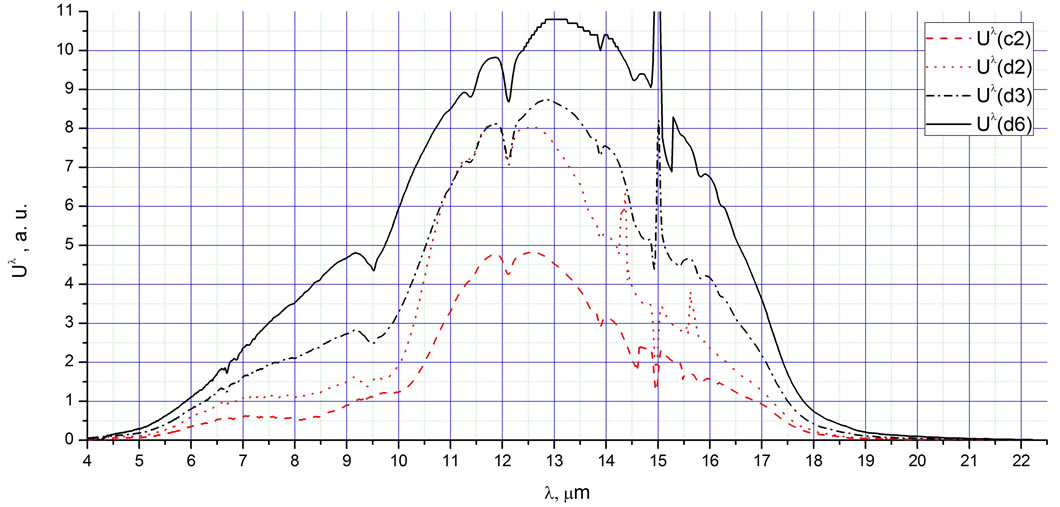
Figure 6. The four radiation spectra Uλ corresponding to maximum amplitudes as intensity increases between c2 and d6.
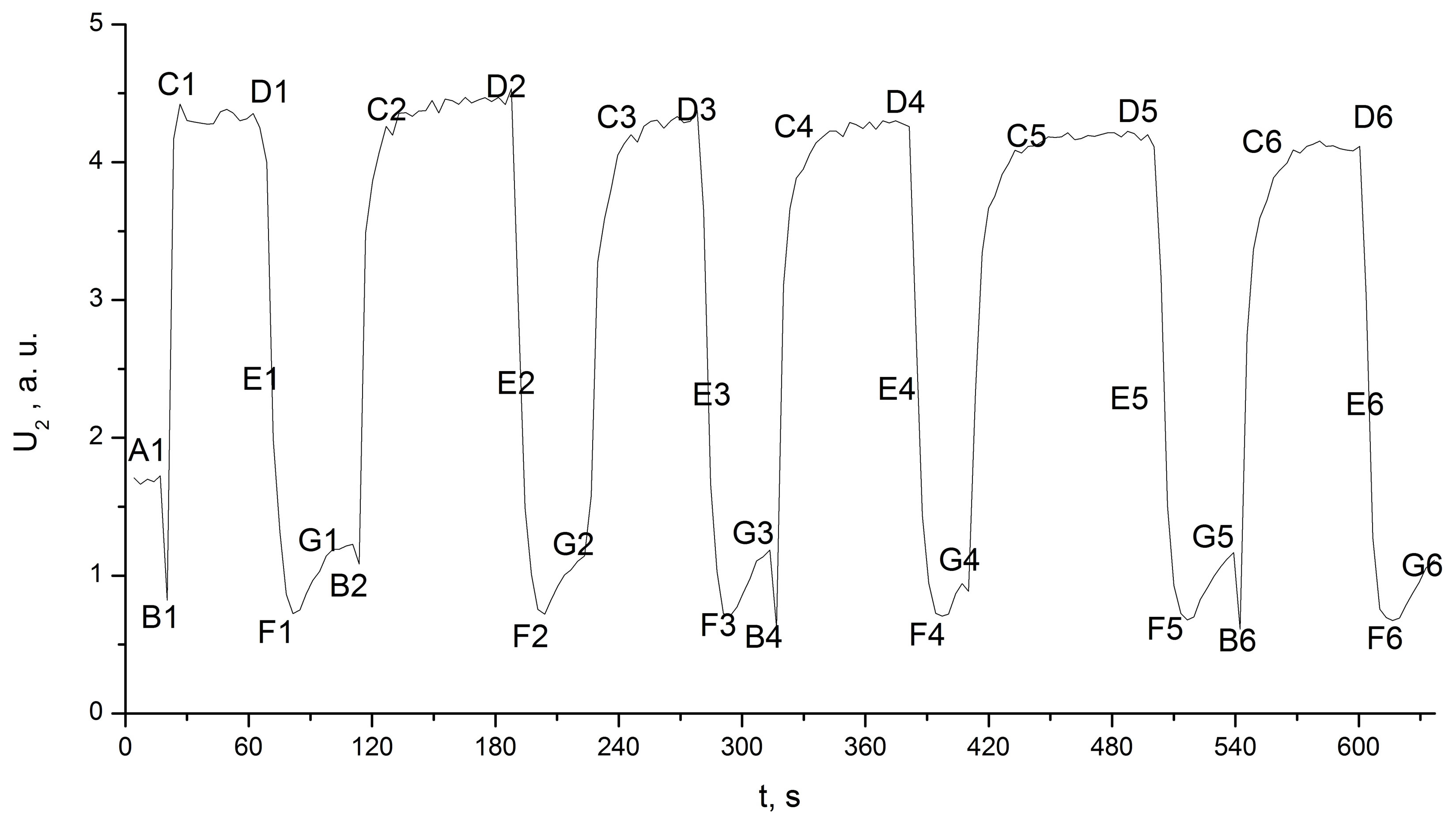
Figure 7. Integral intensity of the IR radiation U2 between 4.0 and 22 µm from the plastic cup vs. the time.
Nichols and Lamar [17] developed an infrared line scan photo camera that scans an object simultaneously with three separate spectral ranges and produces an image of the object as a colour photograph. The three spectral regions are 0.5 - 1.0 µm, 3.0 - 5.5 µm, and 8 - 14 µm. Each of the infrared spectral ranges is rendered in one of the colours: blue, green and red, respectively. As a result, the colour of the objects in the picture indicates their temperature as well as their reflective and emissive properties. The pictures presented by the authors lead to the conclusion that they have indeed found atmospheric sources of infrared radiation that are within the range of 8 - 14 µm and cannot be associated with temperature or reflective radiation. These sources correspond to the underside of cumulus clouds with a temperature of −5˚C (Figures 8(a) and (b)) and to the rising warm air saturated with water vapour. We believe that the PeTa effect is the only plausible explanation for this radiation.
Two of Bordonskiy’s papers [18,19] describe the detection of infrared radiation in the range of 7 - 14 μm with a wide-band radiometer. On July 14, 1987, in the village of Preobrajenka in the Chita region of Russia, the device recorded pulses of radiation at value exceeding those possible from atmospheric noise at 1 km above sea level and in the presence of weak thunderstorm clouds. The recorded pulses corresponded to a radiation temperature of 340 K with a background temperature of 260 K [18]. On December 14, 2006, a similar occurrence was
 (a)
(a) (b)
(b)
Figure 8. (from [17]). Photographs of the same cumulus cloud in different wavelength ranges: (a) Visible range; (b) Infrared 8 - 14 µm range.
reported at the same location [19]. Bordonskiy [20] does not exclude the possibility of PeTa radiation in his experiments.
There are many infrared images of the Earth taken from space. As a rule, a range of 6.9 - 6.7 µm of IR radiation has been particularly useful for recording water vapour in the Earth’s atmosphere [21].
In the case of the water vapour discharge laser, the main emission bands are 119 µm and 220 µm [22], but a few non-identified complementary bands have been recorded in its emission spectrum. One of these, which occurs at 11.83 µm, could be explained as a result of the PeTa effect during the water phase transition.
Highly professional experiments were carried out by Carlon et al. between 1970 and 1979 in the Chemical System Laboratory of the USA Army Armament Research and Development Command [23-28]. The results of these experiments appear to support the existence of the PeTa effect despite other Carlon’s interpretation of these findings.
Unusual results during an investigation of infrared radiation from saturated water vapour were announced for the first time in [23]. One year later, the experimental infrared emission spectra of steam in the 7 - 13 μm wavelength range were presented and analysed [24]. The experimental setup included a recorder instrument fitted with a helium-cooled Ge:Hg detector for these measurements. A circular-variable filter permitted spectral scanning of wavelengths λ in the 7 - 15 µm range. Both 30-s and 60-s scans were used for the trials. Measurements were carried out in a horizontal galvanised sheet-metal pipe that was 175 cm long and 17.5 cm in diameter. The ends of the pipe were partially capped using doughnut-shaped pieces of 6 µm Teflon sheeting with 5 cm holes to maintain steam concentrations within the pipe and to allow optical alignment. The radiometer was aligned at one end of the pipe and was focused on the midpoint of the cavity. A rubber tube entered the pipe tangentially and carried the air to maintain a spiralling, uniform flow of steam within the cavity. The water was boiled from calibrated flasks beneath the pipe at a known rate. Thermistor probes along the pipe gave a temperature profile within the cavity, just above the line-of-sight.
In a typical experiment, steam was introduced into the pipe gradually and its temperature θ was raised to 61˚C. Radiation intensity spectra U(λ) were photographed from the oscilloscope as steam generation progressed at maximum concentrations and during the interesting cooldown periods, which is when the most pronounced aerosol effects were observed. Although there was no adequate explanation of the increase in emittance during cooling, in this and subsequent experiments, the author has recorded such events. These findings are very important, and as a prelude to the main discussion, we would like to underscore that the experiments appear to prove the PeTa effect. Indeed, PeTa radiation is emitted when water vapour and water droplets are in equilibrium; however, during vapour cooling, the PeTa radiation intensity has to be much higher because of condensation.
The steam spectra U(λ) were highly reproducible. As the temperatures of the pipe decreased, there was considerable activity because of water aerosol. Values of the relative emissivity were calculated with the formula ε = U(λ)/Ubb(λ), where Ubb(λ) is the radiation intensity of a black body at the same θ temperature. At θ = 61˚C, representative ε(λ) were 0.965 (7.3 µm), 0.800 (9.0 µm), 0.775 (10.0 µm), and 0.800 (11.1 µm), and these values increased continuously with λ above 11.1 µm, reaching nearly 1.000 for 14.0 µm. The author concluded that the observed emissivities were much larger than those predicted when considering only the contribution of vapour. The predicted values were 0.029 (10.6 µm) and 0.003 (11.1 µm) by Elsasser’s wing model [29] or for other empirical data for water vapour that have been reported in the literature [30]. The author attributed the anomalous emission to tiny water droplets that were too small to produce noticeable optical scattering in the visible wavelengths. Because adequate instrumentation was not available, it was impossible to characterise the aerosols present in those trials.
New instrumentation was developed five years later [25], and it has been used for all of the follow-up experiments [26,27]. We describe these experiments in detail to reinforce our confidence in their experimental design. The equipment used in these measurements included an insulated, cylindrical steel test chamber that was 3 m in diameter and 3 m high. In some trials, the 15 cm diameter viewports were windowless; in other trials, infrared-transmitting polyethylene film windows were used. Because precautions were taken to prevent steam condensation on the windows when they were used, identical results were obtained in either case. The infrared radiometer described above was placed at one viewport. From the ratio of the emittences of the cloud and blackbody at that temperature, the above mentioned unit-less emissivity ε of the cloud could be determined and related to the concentrations of droplets and water vapour present in the chamber at that temperature. The He:Ne laser (wavelength λ = 0.63 µm) and a power meter detector were aligned along an optical axis parallel to that of the radiometer and the target blackbody. The laser and radiometer could thus be used when steam was in the chamber to determine the mean droplet size and mass (volume) concentration; in addition, gravimetric samplers determined the droplet size distributions using sampling probes located along the optical axes.
First, experiments were carried out at a single wavelength of λ = 10 µm to describe the dependency of the emission on the water concentration in the vapour, C, the length of the chamber, L, and the temperature, θ, before introducing further complication due to the spectral dependencies. The data from a typical steam trial (11 experimental points, 74 measurements) are shown in Figure 9. The ordinate is the effective cloud emissivity, ε, discussed previously. The abscissa is a logarithmic scale of cloud droplets CL, g/m2. Cloud temperatures, θ, corresponding to experimental CL values are also shown at the three points of the abscissa. In the original paper, the errors of the temperature and concentration measurements are indicated for every experimental point on the figure. The lower curve allows the comparison of the

Figure 9. (from [26]). Experimental data for effective emissivity, ε, of a typical steam cloud at 10 µm wavelength vs. cloud temperature, θ, and droplet “CL,” g/m2 (the product of droplet mass concentration C g/m3, and the optical path length, L = 3 m). For comparison, the lower curve (labelled D) shows emissivity as calculated for the cloud from a simple model, Equation (1) vs. CL.
observed ε values with those predicted from simple models that disclose the magnitude of the anomaly between the actual and theoretical infrared cloud emissions. The curve was calculated using the simple theoretical equation for emissivity of a partially transparent body or volume acting as a distributed radiator [31]:
 (1)
(1)
where α is the absorption component of the droplet’s mass extinction coefficient, which can be calculated.
The effective (mean) droplet diameter of steam-generated water fogs was known [25], and the author previously performed extensive Mie [31] calculations of the scattering and absorption components of fog droplets at this wavelength. Thus, the author was able to determine, with a high degree of confidence, the contribution to the total observed emission at the 10 µm wavelength as predicted from simple droplet models. It was then possible to subtract the level of anomalous emission because water vapour is not a significant contributor in the 7 - 14 µm atmospheric window region. Above, we mentioned that the unusual emissivity of a vapour/droplet mixture was explained by the author as being caused by the presence of very small droplets [24]. However, their improved instrumentation [25] did not support their hypotheses. Subsequently, Carlon supported the Potter and Hoffman hypotheses [32] regarding the existence of large clusters (11 and 17 molecules) in the water vapour.
Potter and Hoffman [32] carried out experiments in a glass vessel with boiling water and used a sensitive recording system for infrared radiation. An anomalous increase in infrared radiation intensity from the boundary between the glass surface and the condensed vapour was observed. This intensity increased with the increasing condensation rate. The integrated intensity was four times higher than the Plank’s radiation in the range of 1 - 4 µm. Two main emission bands were recorded in the vicinity of 2.10 µm and 1.54 µm. The intensity of the first band exceeded the background radiation by two orders of magnitude. The authors explained the results by the appearance of very specific clusters (7 and 11 molecules) as the water boiled. It is strange that Potter had prepared the special quartz optics for a microscope recording the radiation but boiled the water in a glass vessel [33]. The possibility of recording 4 µm IR radiation through ordinary glass is doubtful. In any case, we decided to verify whether there are some peculiarities of the spectra in the range 1 - 4 µm for our experiments. As we mentioned above, we did not find these spectral peculiarities (Figure 5).
As for Carlon, his logic was as follows: if none of the existing models could explain the experimental results, a water species other than vapour (a monomer) and droplets must exist. In the paper [28], the author insists that the measurements produced three lines of evidence that clusters are present in warm water fogs:
1) The experimental points below the ordinate value of 1.0 in Figure 9 would not seem unusual if they were plotted alone. One would simply assume that enough droplets and vapour were present at a given CL and θ to account for the observed steam cloud emissivity, ε, at λ = 10 µm. However, when one uses actual water vapour and droplet mass concentration data from the chamber instrumentation with simple vapour/droplet models, the expected values of droplet and vapour emissivity are far smaller than the observed values.
2) For higher cloud densities, values of ε > 1.0 were observed similar to those of the “phase transition luminescence” described in the paper [32] and were attributed to water clusters containing c = 11 and c = 17 molecules per cluster.
3) In the emission spectra, features such as “bumps” were observed which were similar to earlier observations in measurements of the infrared continuum absorption [34]; the researchers concluded on other grounds that their results were consistent with the idea that hydrogen bonding contributes to the infrared absorption coefficient of water vapour.
Carlon used the cluster idea but insisted that his observations revealed at least three aspects of investigated phenomena that had not been reported in [32]. They are listed below.
a) Boiling was not necessary for the unusual emission and apparent luminescence of water; cooling water fog clouds well below the boiling point could also produce it.
b) This activity was observed in the 7 - 14 µm range, as well as at 1.5 - 2.1 µm, over a wide range of wavelengths.
c) The observed spectra changed shape with cloud concentration and temperature, abruptly falling to much weaker intensities when saturation humidity was lost.
Additional experiments by Carlon also bear reanalysis [27]. Figure 10 presents a dependence ε (λ) for different θ values and C (368 measurements). As in the experiments at the 10 µm wavelength, the vapour/aerosol emissivity for the full 7 - 14 µm range exceeded the one calculated from the simple emissive model. The author insists that this is evidence of giant clusters: “The existence of anomalous emission investigated at a fixed wavelength such as 10 µm and plotted on the coordinates of Figure 9 requires that consideration be given to the presence of water species other than water vapor or water droplets in cooling steam and water fogs. Additional evidence for clusters in the vapor phase of water is found in our spectral observations, reported here for 7 wavelengths in the 7 - 13 µm infrared window region”.
In Figure 10, every curve corresponds to emissivity for a constant θ and C. For analysis, the author divided all 8 curves into several groups with respect to the influence of various parameters on emissivity. We placed all curves in the same Figure 10, as this offers a more
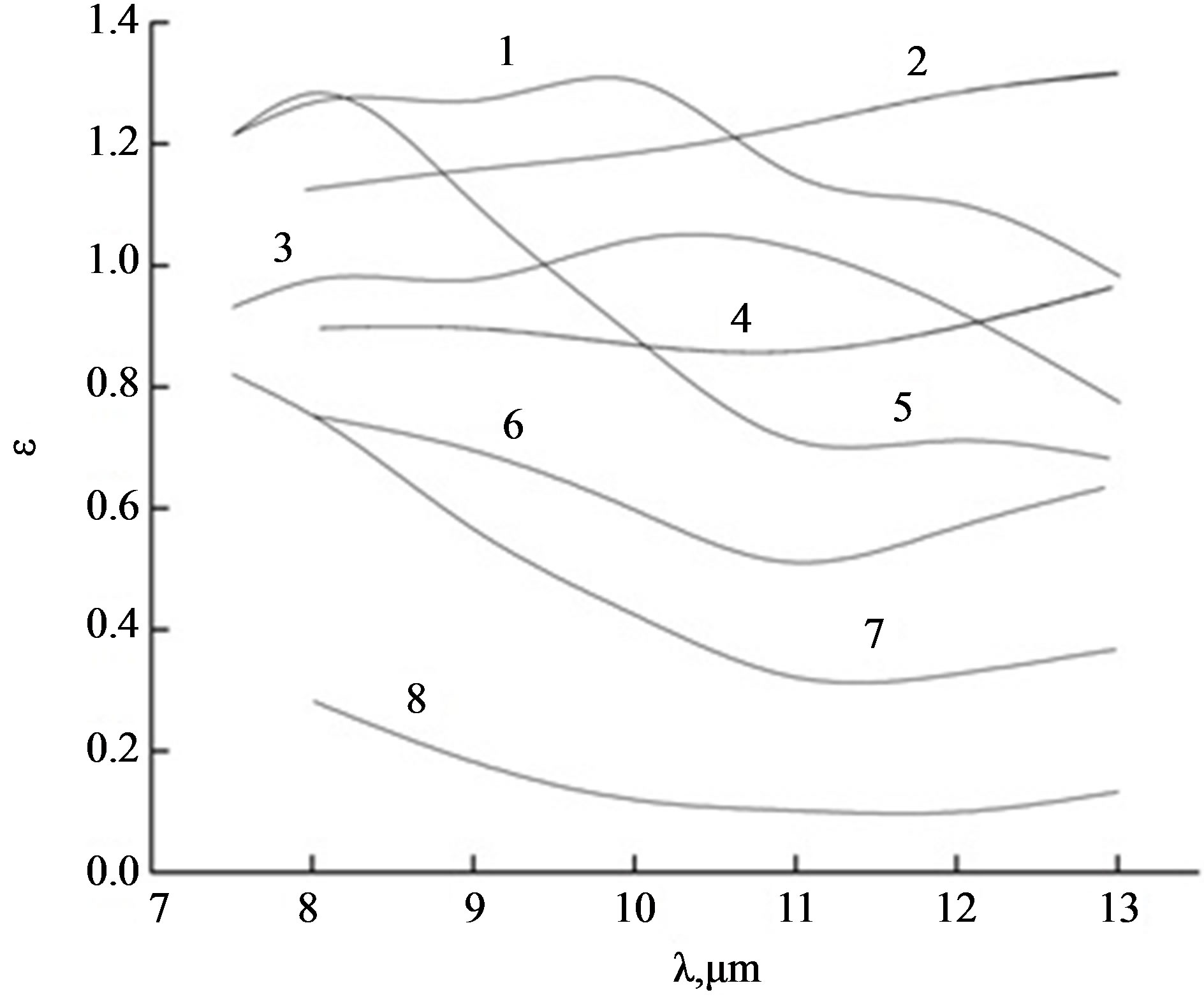
Figure 10. (from [27]). Experimental data showing the effective emissivity, ε, of a typical steam cloud vs. wave-length λ. The curves (1 - 8) correspond to the following droplet mass concentrations, C g/m3, and cloud temperatures, θ˚C: 1 (2.2 ≤ C ≤ 4.0; θ = 30˚C); 2 (4.3 ≤ C; θ = 52˚C); 3 (4.0 ≤ C; θ = 35.3˚C); 4 (2.0 ≤ C ≤ 4.3; θ = 56˚C); 5 (0.5 ≤ C ≤ 1.4; θ = 29.9˚C); 6 (0.6 ≤ C ≤ 1.5; θ = 52˚C); 7 (C ≤ 0.4; θ = 29.5˚C); and 8 (C ≤ 0.3; θ = 52˚C).
objective analysis of the results. For instance, the author confirms that as the cloud cools slightly, the emission spectrum retains a similar shape but increases in intensity. However, Figure 10 shows that it is not correct to investigate the influence of temperature alone. Indeed, spectra 2, 6, and 8 are obtained for the same temperature (i.e., 52˚C). Their shapes are similar, but the ratio of amplitudes is approximately 1:3:6. It could be suggested that C is only a parameter, as shown for Figure 9. Indeed, for spectra 8, 7, 6, 4, 3, and 2, the amplitude ratio is approximately 1:2:3:4:5:6, and it corresponds to the ratio of concentration values: 1.0:1.3:3.5:10.5:≥13.3:≥14.3, but spectra 1 and 5 démodé from this set.
In [28], Carlon mentioned that it is impossible to directly confirm the existence of clusters but that the conclusion follows from the experiments described above. We think this statement to be doubtful. Indeed, if we suggest that the emissivity of vapour/aerosol mixture is proportional to the cluster concentration, it would be expected that the latter must precede changes in emissivity. Accordingly, we present the following lines of evidence: 1) cluster concentration would be proportional to the water droplets’ concentration for 10 µm radiation (Figure 9) as well as for the full 7 - 14 µm range (curves 8, 7, 6, 4, 3, 2 of Figure 10); 2) cluster concentration would increase as the vapour/aerosol mixture cooled; 3) all clusters would periodically disappear for 20-30 sec as is observed in experiments when the level of humidity was less than saturated; and 4) as for the opinion of other specialists, Carlon confirms that his hypotheses of giant clusters did not find a support from specialists in the field. Indeed, as is stated in [35]: “Investigation of absorption spectra of water vapor in the range 5 - 14 µm under temperatures 8 and 110˚C and pressure 760 mm Hg have shown that less than 1% water molecules are associated (We found in different references 0.3%; 0.16%; 0.08%; 0.004%). An upper boundary of complex is 2.3 molecules, i.e., they generally are dimers”.
On the other hand, four peculiarities of PeTa radiation for saturated vapour/aerosol mixtures are notable: a) PeTa radiation does not exist during heating of the mixture because the droplets evaporate; b) At the thermodynamic equilibrium of saturated vapour and droplets, radiation exists because of the emittance of the PeTa radiation by water molecules flowing into the droplets; the intensity of this component increases with the augmentation of full droplet surfaces and is proportional to С/R, where С is a concentration of water droplets and 2R is the diameter of droplets; c) During the cooling of the saturated mixture, radiation appears because of PeTa radiation emittance during the condensation of vapour; this component depends on the rate of temperature change and on the temperature because the absolute humidity of saturated vapour increases with temperature, and the same change of the temperature in different temperature ranges corresponds to different quantities of condensed water; d) With increasing of CL, the absorption and scattering of PeTa radiation also increases.
Thus, the above-mentioned peculiarities of Carlon’s experiments (1 - 4) can be qualitatively explained in the framework of the PeTa model (a - d) without contradictions. To develop a quantitative model, the temperature θ for every measurement must be recorded precisely, along with the speed cooling. Several times in his papers, Carlon has mentioned a rise in emissivity during cooling, but we do not know the rate of cooling. It should be noted that the large volume of the chamber and the intensive convection made difficult, if not impossible, a homogeneous temperature distribution. We believe that the dramatic 20 - 30 s decrease in the emissivity of the vapour/droplet mixture was a result of an uncontrolled increase in the temperature of the measured zone which stopped the PeTa emission.
Mestvirishvili et al. claimed [36] to have recorded intense infrared radiation during water vapour condensation and water crystallization in a closed chamber. The temperature was lowered by adiabatic expansion. The radiation was observed through a Ge window in the chamber. Systems of filters and mirrors were used to select desirable IR ranges from the full spectrum. Radiation was detected by a bolometer. This technique allowed the authors to confirm that they had recorded the characteristic radiation for the condensation in the range of 4 - 8 µm and for the crystallization in the range of 28 - 40 µm. The radiation intensity greatly exceeded the background Plank’s intensity. We doubt the possibility of recording IR radiation in the range 28 - 40 µm through a Ge window. In the paper, neither the details of the experiments nor the full experimental data are presented.
4. Discussion of Experimental Data and Conclusion
Our experiments demonstrate the PeTa effect and allow estimation of both the range and the order of intensity of the PeTa radiation. The main objective of the experiments is to eliminate all doubts that the PeTa effect not only exists but a power PeTa radiation is significant, and it has to be taken in account in all calculations of energetic balance for the atmospheres of the Earth and other planets [5]. Why did we use the temperature of the liquid nitrogen? In the experiments, we would like to be sure that Planck’s radiation does not influence on our results. The deep air cooling allows obtaining of these conditions. Indeed, if we decrease the temperature from 297 K to 77 K the maximum amplitude of the Planck’s radiation moves from 9.9 µm to 37.6 µm, and the integral intensity of equilibrium radiation in the range of our measurement 1 - 25 µm has to be decreased by the factor 3500. We recorded in our experiments increasing of the radiation approximately by the factor 3 in compared with the Planck’s radiation at the room temperature. The four orders effect is sufficient to be sure that it exists. Now every student would be able to repeat the experiments and to investigate the PeTa radiation of this intensity with a very simple infrared detector.
In summary, we compare our experimental results with those from the literature.
The range of the recorded radiation in our experiments coincides with the data of Nichols and Lamar [17], Bordonskiy [18,19], and Carlon [23,24,26,27] that do not give any preference to a specific λ from the range of 7 - 14 µm. Either the nature of the recorded radiation in the previous papers was unknown or its interpretation was questionable.
In our experiments, the radiation occurs during condensation or/and the deposition of the air components. Our results provide the radiation spectra. Apparently, only the PeTa effect can explain this radiation.
On the basis of our experiments, we can conclude that the phenomenon of continuous absorption in the atmospheric window of transparency [29,34] is reliably connected with the PeTa effect.
Although the theory [7,8] seemed to give a satisfactory and, to a certain extent, quantitative explanation of the phenomenon under investigation, this explanation lacked a full quantitative basis.
There are two facets of the experiment that could improve the recording of the energetic balance of the atmosphere. First is the exact PeTa spectrum of the phase transitions of water at the actual temperature and pressure values. Second is the value of the PeTa radiation yield at the same conditions. We hope to be able to present these results in the nearest future.
REFERENCES
- M. E. Perel’man, “Phase Transitions Caused by the Opening of New Channels in Electron-Photon Interactions,” Physics Letters A, Vol. 37, No. 5, 1971, pp. 411-412. http://dx.doi.org/10.1016/0375-9601(71)90609-8
- V. A. Tatarchenko, “Appearance of Distinguishing Features in Emission Spectra during Crystallization of Substances Transparent in the IR Region,” Soviet Physics— Crystallography, Vol. 24, No. 2, 1979, pp. 238-239.
- L. M. Umarov and V. A. Tatarchenko, “Differential Spectra of Crystallization Radiation of Alkali-Metal Halides,” Soviet Physics—Crystallography, Vol. 29, No. 6, 1984, pp. 670-673.
- V. A. Tatarchenko and L. M. Umarov, “Infrared Radiation Accompanying the Crystallization of Sapphire,” Soviet Physics—Crystallography, Vol. 25, No. 6, 1980, pp. 748-749.
- K. Ravilous, “Cloud Power,” New Scientist, Vol. 208, No. 2788, 2010, pp. 38-41. http://dx.doi.org/10.1016/S0262-4079(10)62951-X
- V. A. Tatartchenko, “Characteristic IR Radiation under Crystallization, Sublimation, and Condensation (PeTa Effect),” Scientific Program and Book of Abstracts of 17th International Conference on Crystal Growth and Epitaxy, Warsaw, Poland, 11-16 August 2013, p. 34.
- M. E. Perel’man and V. A. Tatartchenko, “Phase Transitions of the First Kind as Radiation Processes,” 2007, pp. 1-17. arXiv: 0711.3570
- M. E. Perel’man and V. A. Tatartchenko, “Phase Transitions of the First Kind as Radiation Processes,” Physics Letters A, Vol. 372, No. 14, 2008, pp. 2480-2483. http://dx.doi.org/10.1016/j.physleta.2007.11.056
- V. A. Tatartchenko, “Characteristic IR Radiation Accompanying Crystallization and Window of Transparency for It,” Journal of Crystal Growth, Vol. 310, No. 3, 2008, pp. 525-529. http://dx.doi.org/10.1016/j.jcrysgro.2007.11.155
- V. A. Tatartchenko, “Some Peculiarities of First Order Phase Transitions,” Reviews on Advanced Materials Science, Vol. 20, No. 1, 2009, pp. 58-69.
- V. A. Tatartchenko, “Infrared Laser Based on the Principle of Melt Crystallization or Vapor Condensation. Why Not?” Optics & Laser Technology, Vol. 41, No. 8, 2009, pp. 949-952. http://dx.doi.org/10.1016/j.optlastec.2009.04.001
- V. A. Tatartchenko, “Infrared Characteristic Radiation of Water Condensation and Freezing in Connection with Atmospheric Phenomena,” Earth Science Reviews, Vol. 101, No. 1-2, 2010, pp. 24-28. http://dx.doi.org/10.1016/j.earscirev.2010.03.002
- V. A. Tatartchenko, “Infrared Characteristic Radiation of First Order Phase Transitions in Connection with Optics of Atmosphere,” Atmospheric and Oceanic Optics, Vol. 23, No. 4, 2010, pp. 169-175.
- V. A. Tatartchenko, “Nature of Some Sources of Atmospheric Infrared Radiation,” Investigation of Earth from Space, No. 2, 2010, pp. 88-90.
- V. A. Tatartchenko, “The Nature of Specific Sources of Infrared Radiation Recorded by Satellites,” Modern Problems of Distance Probes of Earth from Space, Institute of Space Research of Russian Academy of Sciences, Moscow, Vol. 7, No. 4, 2010, pp. 310-318.
- V. A. Tatartchenko, “Infrared Characteristic Radiation of Water Condensation and Freezing in Connection with Atmospheric Phenomena; Part 2: New Data,” Earth Science Reviews, Vol. 107, No. 3-4, 2011, pp. 311-314. http://dx.doi.org/10.1016/j.earscirev.2011.04.001
- L. W. Nichols and J. Lamar, “Conversion of Infrared Images to Visible in Color,” Applied Optics, Vol. 7, No. 9, 1968, pp. 1757-1762. http://dx.doi.org/10.1364/AO.7.001757
- G. S. Bordonskiy, “Probable Traces of the Laser Emission of Natural Atmospheric Origin,” Atmosphere’s Optics, Vol. 3, No. 4, 1990, pp. 352-355.
- G. S. Bordonskiy and A. A. Gurulev, “Measurements of the Thermal Emission of Chita Atmosphere in the Magnetic Storm of 14 December 2006,” In: G. G. Matvienko and V. A. Banakh, Eds., Abstracts of Fourteenth International Symposium on Atmospheric and Ocean Optics/Atmospheric Physics, Russia, Tomsk, 2008.
- G. S. Bordonskiy, “Retrieval of Active Environments (Remarks on Article of V. A. Tatartchenko ‘Nature of Some Sources of Atmospheric Infrared Radiation’),” Investigation of Earth from Space, No. 2, 2010, pp. 90-91.
- F. Hasler, et al., “NASA/GSFC, the GOES Project,” 2003. http://antwrp.gsfc.nasa.gov/apod/ap020323.html
- W. S. Beyedict, M. A. Pollack and W. J. Tomlinson, “The Water-Vapor Laser,” IEEE Journal of Quantum Electronics, Vol. QE-5, No. 2, 1969, pp. 108-124. http://dx.doi.org/10.1109/JQE.1969.1075731
- H. R. Carlon, “Infrared Emission by Fine Water Aerosols and Fogs,” Applied Optics, Vol. 9, No. 9, 1970, pp. 2000- 2006. http://dx.doi.org/10.1364/AO.9.002000
- H. R. Carlon, “Model for Infrared Emission of Water vapor/Aerosol Mixtures,” Applied Optics, Vol. 10, No. 10, 1971, pp. 2297-2303. http://dx.doi.org/10.1364/AO.10.002297
- H. R. Carlon, M. E. Milham and R. H. Frickel, “Determination of Aerosol Droplet Size and Concentration from Simple Transmittance Measurements,” Applied Optics, Vol. 15, No. 10, 1976, pp. 2454-2456. http://dx.doi.org/10.1364/AO.15.002454
- H. R. Carlon, D. H. Anderson, M. E. Milham, T. L. Tarnove, R. H. Frickel and I. Sindoni, “Infrared Extinction Spectra of Some Common Liquid Aerosol,” Applied Optics, Vol. 16, No. 6, 1977, pp. 1598-1605. http://dx.doi.org/10.1364/AO.16.001598
- H. R. Carlon, “Variations in Emission Spectra from Warm Water Fogs: Evidence for Clusters in the Vapor Phase,” Infrared Physics, Vol. 19, 1979, pp. 49-64. http://dx.doi.org/10.1016/0020-0891(79)90093-9
- H. R. Carlon, “Infrared Absorption by Molecular Clusters in Water Vapor,” Journal of Applied Physics, Vol. 52, No. 5, 1981, pp. 3111-3115. http://dx.doi.org/10.1063/1.329174
- W. M. Elsasser, “Note on Atmospheric Absorption Caused by the Rotational Water Band,” Physical Review, Vol. 53, No. 9, 1938, p. 768. http://dx.doi.org/10.1103/PhysRev.53.768
- P. J. Wyatt, V. R. Stull and G. N. Plass, “The Infrared Transmittance of Water Vapor,” Applied Optics, Vol. 3, No. 2, 1964, pp. 229-241. http://dx.doi.org/10.1364/AO.3.000229
- G. Mie, “Beitrage zur Optik Truber Medien, Speziell Kolloidaler Metallosungen,” Annals of Physics, Vol. 330, No. 3, 1908, pp. 377-445. http://dx.doi.org/10.1002/andp.19083300302
- W. R. Potter and J. G. Hoffman, “Phase Transition Luminescence in Boiling Water; Evidence for Clusters,” Infrared Physics, Vol. 8, 1968, pp. 265-270.
- W. R. Potter, “Infrared Micro-Scanning Measurements of Small Temperature Differences in Aqueous Media,” Master thesis, State University of New York at Buffalo, 1966.
- P. Varanasi, S. Chou and S. S. Penner, “Absorption Coefficients for Water Vapor in the 600 - 1000 cm−1 Region,” Journal of Quantitative Spectroscopy and Radiative Transfer, Vol. 8, No. 8, 1968, pp. 1537-1541. http://dx.doi.org/10.1016/0022-4073(68)90090-3
- G. V. Ukhnevich, “Infrared Spectroscopy of Water,” Moscow, Science, 1973.
- A. N. Mestvirishvili, J. G. Directovich, S. I. Grigoriev and M. E. Perel’man, “Characteristic Radiation Due to the Phase Transitions Latent Energy,” Physics Letters A, Vol. 60, No. 2, 1977, pp. 143-144. http://dx.doi.org/10.1016/0375-9601(77)90409-1
Definition of Abbreviations and Variables (In Order of Appearance in the Text and Figures)
“PeTa effect”: Perel’man-Tatartchenko’s effect.
IRCR under first order phase transitions—infrared characteristic radiation under first order phase transitions (PeTa effect).
MCT: Detector based on Mercury Cadmium Telluride material (abbreviation HgCdTe is either possible).
Δλ: Scan range of spectrometer (µm).
ΔS: Resolution of spectrometer (cm−1).
Sb: Single beam regime.
Cont: Continuous regime of spectrum recording.
IKS-21: Type of Russian spectrometer of 1970th.
Specord-75 IR: Type of the German spectrometer of 1970th.
U1: Integral intensity of radiation from 1.2 to 22.5 µm.
U2: Integral intensity of radiation from 4.0 to 22.0 µm.
Ul(t, λ): Spectral density of measured radiation for the specific wave length, depending on λ (radiation spectrum) as well as t (experiment time from 200 s to 3500 s); t > t1, where t1 is the time corresponding to the transient processes of the spectrometer.
a.u.: Arbitrary units.
mk: In Figures 2 and 7, the specific points of time that correspond to the experimental actions; k corresponds to the cycle number and changes from 1 to 13 (Figure 2) and from 1 to 6 (Figure 7); m corresponds to the action inside the cycle and changes from a to e (Figure 2—aluminium cup) and from A to E (Figure 7— plastic cup):
a (А): Background radiation for room temperature.
b (B): Minimum radiation corresponding to the liquid nitrogen temperature without deposition.
с (C): Point at which stable radiation is achieved.
d (D): Removal of the cup containing liquid nitrogen.
e (E): Period of rapid decrease in radiation after removing the cup containing liquid nitrogen.
f (F): Minimum radiation after the removal of the cup containing liquid nitrogen.
g (G): Increase in the radiation after f (F) because of increasing temperature.
< Ul(c7, c8,∙∙∙, c12)>: Averaging the spectrum at the discreet points c7, c8, c9, c10, c11, c12 T: Absolute Kelvin temperature.
316.7 s (b1): Example of the spectrum definition (means: spectrum recorded at experiment time 316.7 s, which corresponds to point b1 at Figure 1).
θ: Vapour cloud temperature ˚C.
ε = U(λ)/Ubb(λ): Relative emissivity.
Ubb(λ): Radiation intensity of a black body.
CL: Optical way, where C is the concentration of water in the vapour, L is the length of the chamber.
α: Absorption component of a droplet mass extinction coefficient.
c: Quantity of molecules in a cluster.
2R: Droplet diameter.
NOTES
*Corresponding author.
1Definition of abbreviations and variables either is at the end of the paper.

