Optics and Photonics Journal
Vol.3 No.4(2013), Article ID:35616,19 pages DOI:10.4236/opj.2013.34041
New Approaches in Frequency Conversion of Laser Radiation in Plasma Plumes
Institute of Ion-Plasma and Laser Technologies, Tashkent, Uzbekistan
Email: rashid_ganeev@mail.ru
Copyright © 2013 Rashid A. Ganeev. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received May 3, 2013; revised June 8, 2013; accepted July 12, 2013
Keywords: High-Order Harmonic Generation; Laser Plasma; Ultrashort Laser Pulses
ABSTRACT
Recent studies of plasma harmonic generation are reviewed. We show the advances of this technique for generation of coherent ultrashort pulses in the extreme ultraviolet range. Among the achievements highlighted in this review are the comparative experimental and theoretical studies of high-order harmonic generation in silver plasma, isolated subfemtosecond pulse generation in Mn plasma ablation, stable generation of high-order harmonics of femtosecond laser radiation from laser produced plasma plumes at 1 kHz pulse repetition rate, and high-order harmonic generation in fullerenes using fewand multi-cycle pulses of different wavelengths. We show that new developments of plasma harmonic studies can lead to the creation of an attractive field of laser ablation induced high-order harmonic generation spectroscopy.
1. Introduction
Coherent short wavelength radiation is of increasing importance for a broad variety of basic and applied research in various fields of physical, chemical, and life sciences. Among them, femtosecond time-resolved coherent diffractive imaging and photo-induced processes at surfaces and nanoparticles, as well as lithography, plasma diagnostics, and materials processing and diagnostics are of foremost interest. The high-order harmonic generation (HHG) from femtosecond laser pulses allows producing coherent radiation in the extreme ultraviolet (XUV) spectral range. Table-top lasers render these processes possible with the prospect of wide-spread scientific applications. Presently, predominantly few gases are employed as target media for HHG. Other efforts rely on the creation of harmonics at solid surfaces, either by a coherent wake field excitation or, for petawatt class lasers, on a relativistically moving electron gas acting as a plasma mirror. So far, however, only low conversion efficiencies have been obtained, despite the enormous efforts. Other methods include XUV free-electron lasers and X-ray lasers.
To promote the use of XUV radiation it seems therefore appropriate to advance laboratory scale sources to a higher application level. Many interesting experiments can be performed by HHG based on laboratory scale femtosecond lasers. These sources may cover the spectral range between 10 and 100 eV photon energy of harmonics, and with few-cycles laser systems even up to several 100 eV. For practical applications of high-order harmonic sources higher conversion efficiency and thus an increase in the photon flux and also of the maximum photon energy of the harmonic radiation would be beneficial. HHG itself can be used as a spectroscopic tool for analysis of the optical, nonlinear optical and structural properties of the emitters of harmonic generation presently comprising on a few noble gases. The generation of high-order harmonics in laser-produced plasmas from various solid-state targets, being for this purpose a relatively new and largely unexplored medium, promises to yield these advances.
Most interestingly, recent studies have shown that enhanced high-order harmonics can be generated also from the ablated nanoparticles, which opens the prospects for applications of local field enhancement, broad plasmonic resonances and a more efficient recombination processes for plasma HHG. As a highly interesting perspective an increase of the harmonic output by quasi phase matching in specially prepared plasmas may be considered. For the plasma a different and more flexible technique than used in neutral gases can be applied. The plasma may be spatially modified using a long pulse co-propagating with the fundamental driving pulse, and conditions might be found where quasi phase matching is possible over a long distance in the plasma, while the constructive and destructive interference of harmonic waves in such plasmas containing different emitters can provide a new knowledge about the phase-related characteristics of this process. Thus the above approach can be useful for producing an efficient source of short-wavelength ultra-short pulses for various applications and studies of the properties of harmonic emitters. The laser ablation induced high-order harmonic generation spectroscopy is a new method for the studies of material science and can be considered as one of the most important applications of HHG.
In this review, we discuss the realization of new ideas emerged during last few years, which further improved the HHG efficiency through harmonic generation in specially prepared plasmas and allowed the spectral and structural studies of matter through the plasma harmonic spectroscopy. We also present the current status of plasma HHG studies, and show new trends and perspectives in the developments of this filed.
The structure of the review is as follows. In Section 2, the comparative experimental and theoretical studies of high-order harmonic generation in silver plasma are discussed. Isolated sub-femtosecond pulse generation in the XUV range using Mn plasma ablation is analyzed in Section 3. Section 4 is devoted to the methods of stable generation of the high-order harmonics of femtosecond laser radiation from laser produced plasma plumes at 1 kHz pulse repetition rate. HHG in fullerenes using fewand multi-cycle pulses of different wavelengths is discussed in Section 5. Short summary remarks presented in Section 6 give some clues on future developments and perspectives of this interesting field of optics.
2. Studies of HHG Cut-Off in Silver Irradiated by Femtosecond Pulses
In this Section, we present the results of theoretical and experimental study of HHG in the ensemble of silver particles irradiated by intense femtosecond pulses of Ti:sapphire laser. It is shown that the photoemission spectra exhibit unusual behavior when the laser field strength approaches near-atomic values. In subatomic field strength the cut-off frequency increases linearly with laser pulse intensity. However, when the field strength approaches near-atomic region firstly cut-off frequency slows down and then saturates. To give new interpretation of such kind of photoemission spectrum behavior the light-atom interaction theory based on the use of eigenfunctions of boundary value problem for “the atom in an external field” instead of the traditional basis of the “free atom” eigenfunctions has been proposed.
In spite of the twenty-year history, the effect of the HHG is still under a great interest of both experimentalists and theoreticians. The origin of this interest is manifold. From a practical point of view, the HHG is one of the effective mechanisms for producing a coherent emission in a broad range of electromagnetic wave spectrum. The presence of plateau region in the harmonic amplitude distribution in XUV region affords grounds for development of sub-femtosecond pulse formation methods. As a result, the new frontiers are opened up in science by extending the nonlinear optics and time-resolved spectroscopy to the XUV range [1] and pushing ultrafast science to the attosecond domain, enabling the XUV spectroscopy and imaging of molecular orbitals [2], surface dynamics [3], and electron motion. The HHG is the reliable route to produce attosecond light pulses [4,5] and is therefore fundamental to attosecond science [6].
At present days, the efficiency of conversion to highorder harmonics is really too small to consider this emission as a real coherent XUV source for biology, plasma diagnostics, medicine, microscopy, photolithography, etc. Hence, the search for ways of increasing the cut-off frequency and the HHG efficiency in the XUV spectral range is still among the most topical problems of nonlinear optics.
The plasma HHG was observed with the large number of periodic table elements having usually small and middle atomic numbers [7-12]. As a rule, the interaction medium is a laser plasma that is prepared by irradiation of metal surface by picosecond pulses. The maximum harmonic order, or the cut-off frequency (CF), obtained in plasma media to date varies from the sixties to seventies harmonics of fundamental frequency [12] of Ti:sapphire laser. The highest-order harmonics (the 101st harmonic, λ = 7.9 nm) have been obtained in manganese plasmas [9]. The efficiency of conversion in the plateau region amounts to ~10−5 [10]. This value depends on both atomic energy level diagram and laser pulse parameters (intensity, energy and duration, carrier-envelope phase). The CF movement into the sub-nanometer region promises new possibilities in creating XUV coherent sources. Hence, the study of the CF dependence on the irradiated media properties and external laser pulse parameters is the problem of significant scientific and technical interest. Recently, the CF values corresponding to sixties and above harmonics have been obtained in experiments with silver plasma [10,11] and this stimulated to choose this medium for numerical simulations and compare the obtained results with the experimental data.
The traditional interpretation of the harmonic generation is usually based on the model of three-stage process that comprises the ionization of an atom, the electron acceleration in the electromagnetic field, and its subsequent collision with ion. This process is periodically repeated every half cycle of the electromagnetic wave. The evolution of the ionized electron is usually described with the help of Volkov wave functions or classical mechanics equations. It should be noted, that the use of the Volkov wave functions is due to the temporal evolution of the continuous spectrum electron wave functions in the presence of the laser field. At the same time, the spatial profile of the discrete spectrum wave functions is also changed in the presence of the external electromagnetic field. However, in the limit of zero strength fields the Volkov wave functions are transformed to the free electron wave functions, while the discrete spectrum wave functions became the atomic eigenfunctions. Hence in the weak or zero fields the eigenfunctions of discrete and continuous spectra are not mutually orthogonal and they do not compose the complete basis of the orthogonal functions. This is the most principle inconsistence of the above methods.
In those studies, the analysis was focused on the single silver atom photoemission spectra [13]. The most unusual feature of the single atom photoemission spectra is the CF saturation effect. The CF saturation means that the maximum observed harmonic order ceases to be intensity dependent at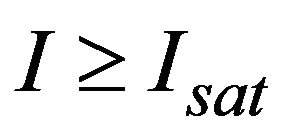 . For the first time, the effect of the CF saturation in silver plasma was experimentally observed in [10]. The maximal order of experimentally observed harmonic is equal to 71. On the other hand, the results of computer simulations performed for the single silver atom [14] have shown that the CF is saturated in the region of over atomic field strength, but at near atomic field strength the maximal order of generated harmonics is much higher than that observed experimentally. The main purpose of the presented study is to explain the difference between the experimental and theoretical results and to provide the interpretation of the main mechanisms lying in the origin of the CF saturation effect.
. For the first time, the effect of the CF saturation in silver plasma was experimentally observed in [10]. The maximal order of experimentally observed harmonic is equal to 71. On the other hand, the results of computer simulations performed for the single silver atom [14] have shown that the CF is saturated in the region of over atomic field strength, but at near atomic field strength the maximal order of generated harmonics is much higher than that observed experimentally. The main purpose of the presented study is to explain the difference between the experimental and theoretical results and to provide the interpretation of the main mechanisms lying in the origin of the CF saturation effect.
To study the high-order nonlinearities through the HHG, the silver target was placed inside the vacuum chamber to ignite the plume by laser ablation of this sample. Silver has previously proven to be most efficient medium for production of the plasma plumes where the highest HHG efficiency (8 × 10−6) in the XUV range was observed [15].
The pump source was a commercial, chirped pulse amplification laser system, whose output was further amplified using a homemade three-pass amplifier operated at a 10 Hz pulse repetition rate. A heating pulse was split from the amplified laser beam by a beam splitter before a pulse compressor (Figure 1). The heating pulse duration was 210 ps. A spherical lens focused the heating pulse on the target placed in the vacuum chamber. The area of ablation was equal to 0.5 mm2. The heating picosecond pulse intensity at the target surface was varied in the range of Ipp = (0.5 – 5) × 1010 W∙cm−2 by changing the energy of heating pulse. A driving femtosecond pulse at a centre wavelength of 792 nm had the energy of 12 mJ and pulse duration of 150 fs after propagation of the compressor stage. After the proper delay with regard to the heating pulse irradiation (20 - 80 ns), the driving pulse was focused by a spherical lens (f/10) on the ablation plume from the orthogonal direction. The maximum intensity of the driving pulse at the focal spot could reach 6 × 1016 W∙cm−2. The position of laser focus was adjusted to be either before or after the laser plume to exclude the influence of considerable ionization of the silver neutrals and ions in laser plume and to maximize the harmonic yield. The intensity of the driving femtosecond pulse (Ifp) at the plasma area was adjusted between 1×1014 and 1×1015 W∙cm−2. The distance between the HHG interaction area and target surface was varied in the range of 100 - 200 mm. The spectrum of generated highorder harmonics was analyzed by a grazing incidence XUV spectrometer with a gold-coated flat-field grating. The XUV spectrum was detected using a microchannel plate (MCP), and the optical output from the phosphor screen was recorded using a charge-coupled device (CCD) camera.
Figure 2(a) shows the image of harmonic spectrum from Ag plasma at the conditions when the femtosecond pulse was focused after the plasma plume. The harmonics up to the 55th order were routinely observed at these
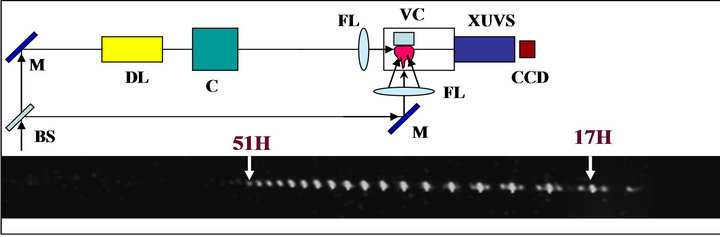
Figure 1. Experimental setup for HHG in silver plasma. BS, beam splitter; M, mirrors; DL, delay line; C, compressor, FL, focusing lenses; VC, vacuum chamber; XUVS, extreme ultraviolet spectrometer; CCD, charge coupled device. Inset: Typical image of harmonic distribution from 17th to 51st orders [13].
17 55
 (a)
(a) (b)
(b)
Figure 2. (a) Harmonic spectra from silver plasma in the case of focusing behind the plasma area; (b) Spectral image of harmonics from silver plasma in the case of aperturing the input femtosecond radiation. Numbers show the harmonic orders [13].
conditions, when the intensity of femtosecond pulse at the plasma area was Ifs = 2.5 ´ 1014 W∙cm−2. Note that divergences of harmonics at the beginning of plateau-like distribution of harmonics and at the cut-off region were approximately equal to each other. The increase of laser intensity at the plasma area led to increase of harmonic cut-off (Hc) up to the 61st order. The divergence of harmonics gradually increased with the growth of harmonic order and the divergences of the lowest (17th - 25th) were approximately two to three times less compared with the highest (45th - 57th) harmonics.
At these experimental conditions (focusing inside the plasma plume, intensity of the driving pulse at the plasma area Ifs = 4 ´ 1014 W∙cm−2, delay between the pulses of 30 ns) the divergence of driving radiation was changed by introducing the aperture in front of the input window of vacuum chamber through which femtosecond radiation propagated toward the plasma plume. A decrease of beam sizes led to considerable deformation of observed spectra, when one can find the conditions of variations of the divergence of harmonics in different ranges of harmonic spectra, as well as considerable re-distribution of harmonic efficiency along the plateau region. When the aperture was decreased down to 4 mm (and correspondingly decreased the energy of propagated radiation from 12 mJ to 4 mJ) a remarkable pattern of harmonic spectra appeared showing the five to ten times enhancement of harmonic intensity along the axis of laser propagation for higher harmonics compared with lower ones (Figure 2(b)). The on-axis intensities of 11th - 19th harmonics were considerably less than those in the range of 25th - 47th orders.
The Hc(Ifp) dependence became saturated at Ifp » 4 × 1014 W∙cm−2 (see Figure 3" target="_self"> Figure 3 showing the dependence between the maximum observed harmonic order and the femtosecond pulse intensity). This intensity is well above the one at which the neutral Ag atoms are ionized. So it may be an additional indication of the crucial role of singly charged ions in generation of high-order harmonics.

Figure 3. Harmonic cut-off from silver plasma as a function of laser intensity. The saturation of Hc(Ifp) dependence was started at ~4 × 1014 W∙cm−2 [13].
The novelties of these experiments are 1) the observation of the efficient harmonic generation for the high orders, while keeping the low-order ones at smaller conversion efficiency; and 2) the observations of saturation of the HHG yield above some level of laser intensity (4 × 1014 W∙cm−2). The aperturing of laser beam led to better phase matching conditions for higher orders compared with lowest harmonics (Figure 2(b)). The intensity of those high-order harmonics became strong enough to allow the observations of second-order diffraction patterns from the grating (see the lobes from the left and right sides of lowest harmonics on Figure 2(a)).
The violation of the phase-matching conditions at high intensities of driving radiation is caused by appearance of the additional free electrons possessing positive dispersion, which does not match with the relatively low dispersion of atoms and ions. The difference with the case of analogous observations in the gaseous media is related with presence of the free electrons at the initial state of plasma media. The ablation at appropriate conditions can create the formation of “optimal” plasma, which, whilst containing free electrons, does not prevent the violation of phase matching. Only additional free electrons appearing during further ionization of singly charged ions of silver (second ionization potential of silver is 21 eV, which corresponds to the breakdown saturation intensity of laser radiation of ~3 × 1014 W∙cm−2).
Silver is one of most attractive targets for plasma formation and HHG. Conversion efficiency reported for this plasma medium for the harmonics in the range of photon energies of 50 - 80 eV (8 × 10−6, [10]) is the highest among other plasma plumes. Moreover, the value of conversion efficiency is the same, as those reported in the case of gas HHG studies. Assuming the stability amendments in the harmonic generation from this plasma (of the order of 1 million shots at 1 kHz pulse repetition rate [16]) one can anticipate a robust application of this target for various applications of plasma HHG spectroscopy.
The process of a light-atom interaction becomes fundamentally the non-resonant process, when the laser pulse temporal width approaches to a few cycles of optical oscillations. Indeed, in this case the energy of such pulse is comparable or exceeds the energy level difference between the free atom states. Hence, the well developed theories of the resonant oneor multi-photon interactions cease to be valid in this case. Moreover, the binding energy of atomic electrons tends to zero when the laser field strength exceeds the intra-atomic field strength, because the electron moves mainly in the spatial regions, which are far from its parent nuclei. It is evident that the basis of a free atom eigenstates could not serve as a useful basis for the wave function expansion when the laser field strength approaches to the intra-atomic values. At the same time, as it has been shown in [17], there are direct mathematical relationships between the eigensolutions of the “free atom” boundary value problem and boundary value problem for “the atom in an external field”.
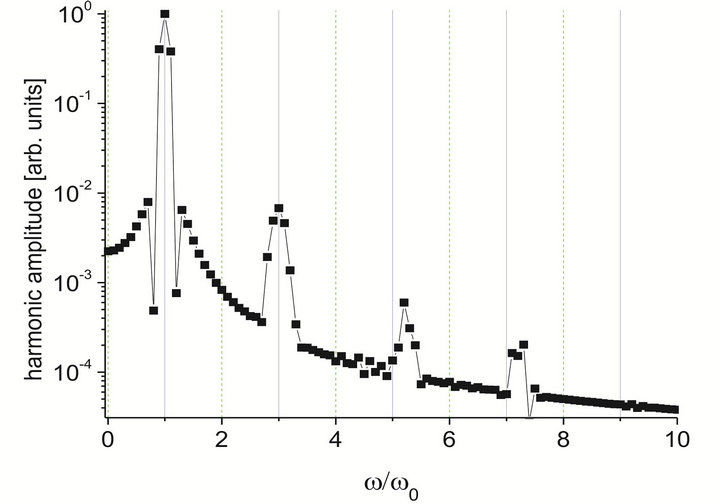
The numerical calculations yield a series of harmonic emission spectra from silver particles. At small intensities, in subatomic region the spectrum consists of the sequence of the odd harmonics of incident field carrier frequency (Figure 4(a)). The amplitudes of harmonics
 (a)
(a)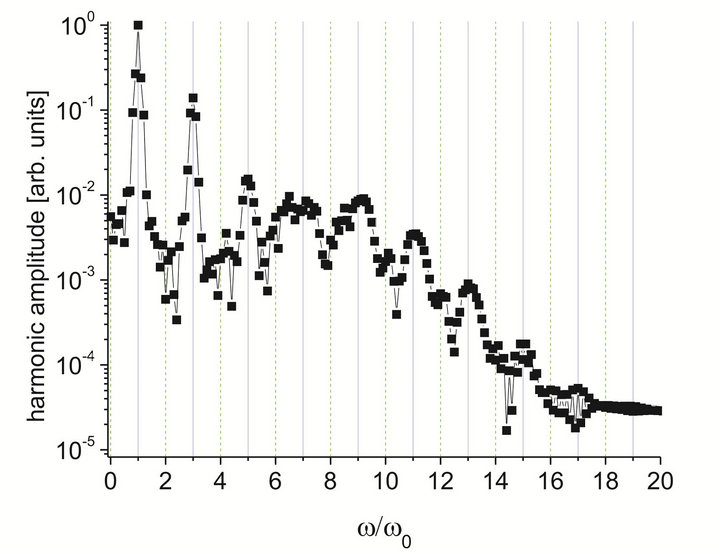 (b)
(b)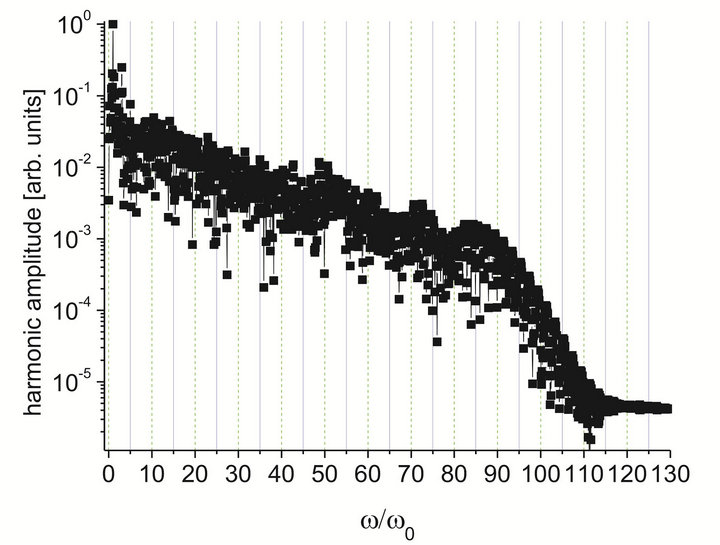 (c)
(c)
Figure 4. The photoemission spectra generated in silver at the laser pulse intensities of (a) 5.94 × 1010; (b) 1.83×1012, and (c) 1.88 × 1013 W∙cm−2 [13].
sharply drop with the harmonic number. The origin of this emission is the light-induced (and, hence, time dependent) anisotropy of a spatial profile of an electron wave function: the electromagnetic wave induces the radial electron motion in the intra-atomic potential field and, hence, produces some external work. This motion will inevitably result in the appearance of harmonics. At a given laser field strength this process could be due to elastic light-atom interaction, because after the termination of the laser pulse action the atomic electron can be again found in the ground state.
When the laser field strength approaches 3 × 1011 W∙cm−2, the shape of the response spectrum is changed. At higher intensity, there appear tendencies for growing of its width and formation of plateau (Figure 4(b)). Further increase in the amplitude of the external field strength allows to observe well-defined plateau with definite CF (see Figure 4(c) for I = 1.88 × 1013 W∙cm−2).
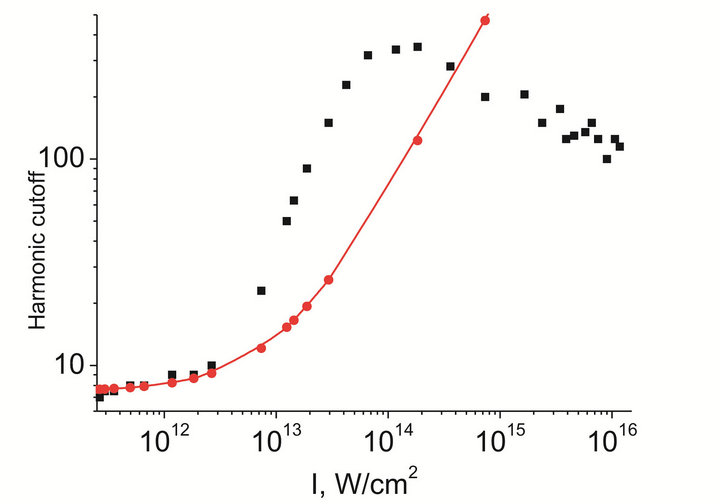
The results of computer calculations of the CF as a function of the laser pulse intensity is presented in Figure 5(a). The solid line in this figure shows the approximated analytical dependence obtained for a silver atom
 (a)
(a)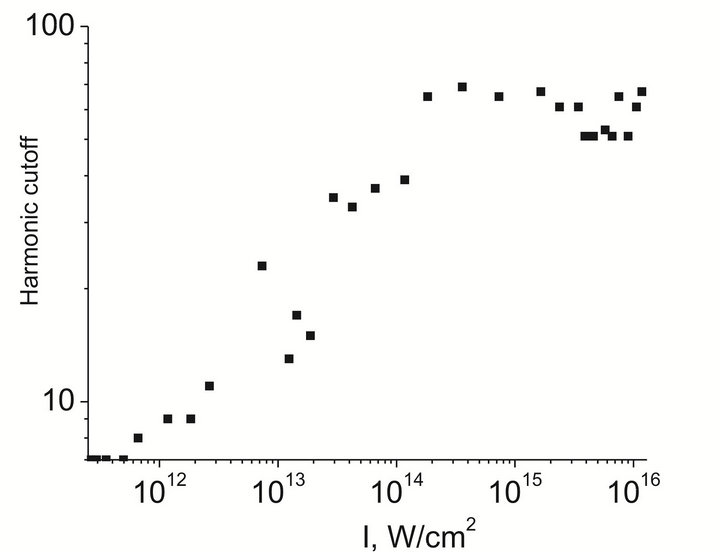 (b)
(b)
Figure 5. (a) Cut-off frequency as a function of the laser pulse intensity. Squares are the result of numerical calculations, solid line with circles is the dependence given by the approximation discussed in [13]; (b) Cut-off frequency of an ensemble of atoms as a function of a laser pulse intensity [13].
in the frames of the approximation discussed in [13]. In the region of the laser pulse intensity of 1011 < I < 1012 W∙cm−2 the results of computer calculations are in good agreement with the proposed approximation. Under further increase of the laser pulse intensity the calculated curve raises faster than it is predicted by the proposed approximation. In this region of pulse intensity the population of other discrete excited states becomes comparable and even exceeds the population of  state of Ag due to the recombination process. Hence, the new channels of photoemission are revealed.
state of Ag due to the recombination process. Hence, the new channels of photoemission are revealed.
At laser pulse intensity I > 1014 W∙cm−2 the CF is saturated, i.e., it ceases to be intensity dependent. The reason of such behavior is quite obvious and it is associated with the fact that the probability of an electron ionization approaches to unity in this region of a pulse intensity. It means that the atomic electron is almost entirely localized in the continuum spectrum states and it does not collide with its parent ion. At the same time, as far as the time profile of a laser pulse has relatively soft slope in the front of pulse, hence, the harmonics are effectively generated here. So, the results of computer modeling show that the most probable reason of the CF saturation is the total ionization of the irradiated atom.
One can see from Figure 5(a) that the calculated laser pulse intensity Icalc » 1014 W∙cm−2 at which the CF is saturated is close to the experimentally measured value (Iexp = 4 × 1014 W∙cm−2). However, the calculated maximal order of harmonics exceeds the experimentally measured value for more than four times. In computer simulations we deal with a single silver atom. Hence it is natural to assume that the reason of this difference can be due to the frequency dependent dispersion appropriate to the spatially distributed ensembles of atoms.
The dispersion properties of a spatially distributed ensemble of atoms could result in drastic transformation of an atomic ensemble emission spectra in comparison with the single atom one. Figure 5(b) shows the integral dependence of the CF as a function of laser pulse intensity, which is calculated for spatially distributed ensemble of atoms. It was taken into account in these calculations that the ionization probability depends on the peak pulse intensity. It can be seen that the curve in Figure 5(b) fits much closer to the experimentally measured dependence.
Summarizing this section, the saturation of the CF of the photoemission spectra generated in a silver by a femtosecond laser pulses has been demonstrated both experimentally and theoretically. In experiments with 155 fs pulse of Ti:sapphire laser the highest experimentally measured harmonic was 61 and the saturation intensity of Iexp = 4 × 1014 W∙cm−2. The theoretical analysis is based on the non-perturbative theory of nonlinear response, which enables to vary the laser field strength in a wide region from a subatomic to a over-atomic values. The results of computer simulations have shown that the CF is also saturated, but the maximal harmonic order exceeds three hundred in the case of single atom. This drastic difference between experimental and theoretical results is due to the dispersion effects, which play a decisive role in the spatially distributed ensemble of ionized atoms. At given experimental conditions the phase mismatch between the driving laser pulse and the harmonic emission modifies significantly the frequency spectra of an atomic ensemble in comparison with the single atom response. The amplitudes of high-order harmonics are significantly suppressed. The simplest way to avoid this modification is to decrease the atomic density. However, this way is in contradiction with the perspectives of practical applications of the high-order harmonic emission.
3. Isolated Sub-Femtosecond XUV Pulse Generation in Mn Plasma
In this section, we discuss HHG from transition metal plasmas. These are very promising targets in view of the giant resonances found in the photoionization cross sections. For example, the Mn+ cross section is ~40 Mb at 50 eV photon energy, whereas rare gas atoms have cross sections between 1 and 8 Mb at this photon energy. Photorecombination-the third step in the recollision model-is the inverse process of photoionisation and therefore HHG and photoionization must exhibit the same resonances. This has been confirmed not only by previous resonance-induced experiments with laser-produced transition metal plasmas but also in a recent study of HHG from xenon gas [18].
Resonance-induced enhancement of a single harmonic of the laser radiation allowed considerable improvement of harmonic efficiency in some specific XUV spectral ranges related with high oscillator strengths of ionic states of metals. This was confirmed in multiple studies following the initial observation of this phenomenon in indium plasma [19]. In particular, strong enhancement of a single harmonic was reported in Cr [20] and Mn [9] plasmas. The Mn plasma is of special interest since it showed the highest harmonic cut-off energy observed in plasma plumes (101st harmonic of Ti:sapphire laser [9]). In previous studies, multi-cycle (30 fs [9] and 140 fs [21]) laser pulses were employed and the generation of all harmonics in the plateau was observed together with a strongly enhanced harmonics in the vicinity of 50 eV.
Recent progress in the generation of few-cycle pulses allowed the observation of various new effects including the realization of isolated attosecond pulse generation in gas media [22-24]. In this connection it is interesting to analyze resonance-induced processes observed in an ablation plume using the shortest available laser pulses. Below, we present the analysis of the experiments on resonance enhancement in manganese plasmas using 3.5 fs pulses [25]. The most interesting feature observed in those experiments was a suppression of almost all neighboring harmonics in the vicinity of a resonantly enhanced single harmonic at the photon energy of ~50 eV.
The experimental arrangements were analogous to those presented in previous section of this review, excluding the use of few-cycle pulses for the experiments under consideration. The harmonic spectrum in the case of propagation of the 3.5 fs pulses through the manganese plasma was strikingly different compared with other plasma samples (for example Ag plasma) analyzed in separate experiments. While all other samples studied showed a relatively featureless harmonic spectra with extended cut-off (Figure 6, upper curve showing spectrum of the harmonics generating in the silver plasma), the Mn plasma allowed generation of a strong single harmonic substantially enhanced compared with neighboring ones (Figure 6, bottom curve).
As it was already mentioned, the harmonic spectra from manganese plasmas for 30 fs and 140 fs pulses also showed enhanced harmonics around 50 eV. The assumption of the resonance nature of the enhancement of harmonics of the ~800 nm radiation of Ti:sapphire lasers in this spectral region is supported by the presence of a strong giant resonance in the vicinity of 50 eV confirmed by experimental [26] and theoretical [27] studies. The enhancement of a single harmonic can be attributed to the broadband resonances of the ions of few metals, such as V, In, Cd, Cr, Cd, and Mn. These “giant” resonances have been experimentally confirmed in the literature [26,28,29] and discussed recently in a few theoretical studies [7,30-32].
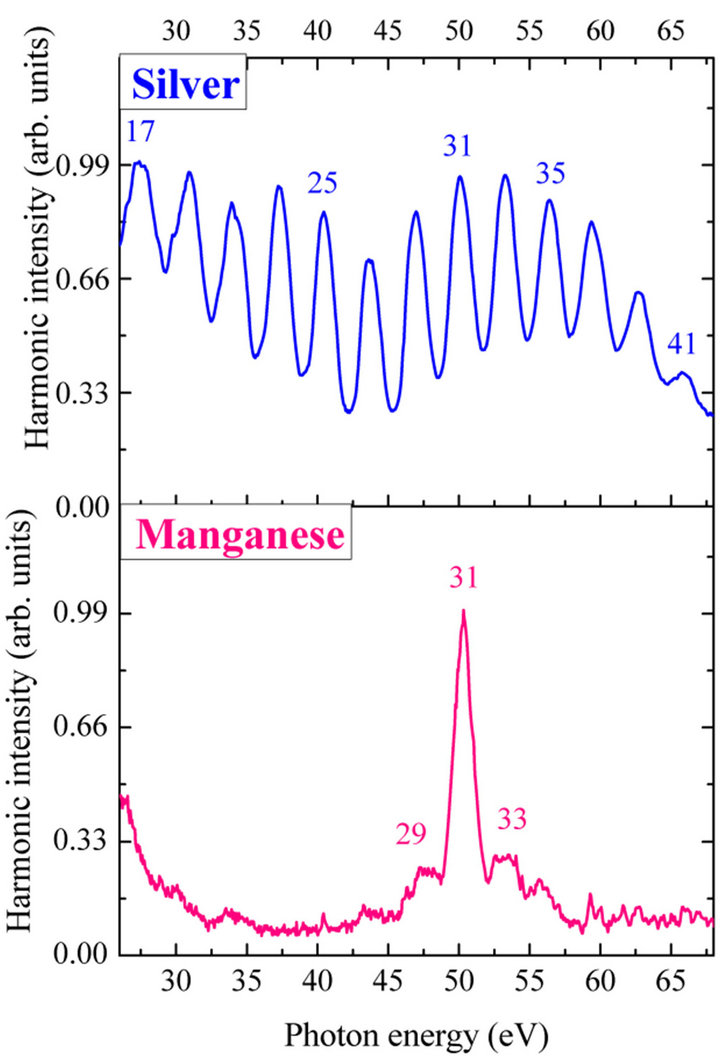
Figure 6. Harmonic spectra from the silver plasma (upper curve) and manganese plasma (bottom curve) [25].
However, in previous studies using multi-cycle pulses, the intensity of enhanced harmonics was only a few times higher compared with those neighboring harmonic orders. The same features were reproduced in the reviewed studies using 40 fs pulses from another Ti:sapphire laser at similar intensity inside the laser plasma (4 × 1014 W∙cm−2). The raw image of the harmonic spectrum presented in Figure 7(a) shows several enhanced harmonics starting from the 31st order followed by an extended second plateau. The extension of the harmonic cut-off exceeding the 71st order is attributed to the involvement of doubly charged Mn ions as the sources of HHG. This feature of Mn plasma harmonics has already been reported earlier [9]. Here also presented a typical image of a Mn harmonic spectrum in the case of 3.5 fs pulses (Figure 7(b)). No second plateau, which was seen in the case of multi-cycle (40 fs) pulses, is observed for the few-cycle pulse. Most striking was the observation of a single, very strong, broadband (2.5 eV)
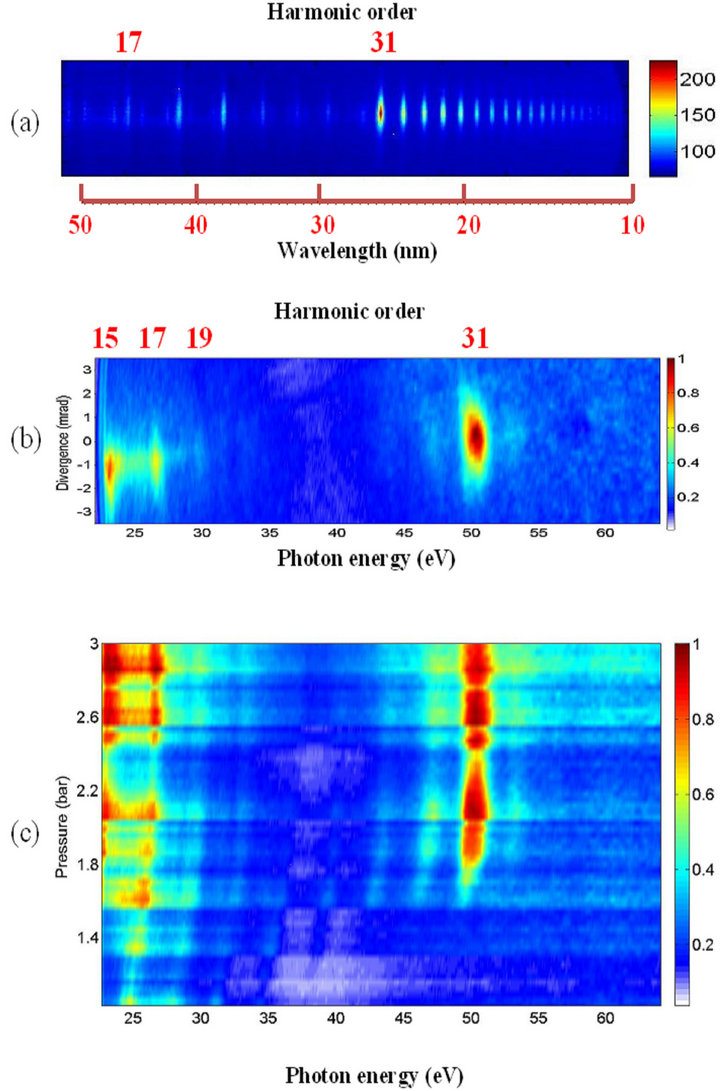
Figure 7. Raw images of harmonic spectra from manganese plasma in the case of (a) 40 fs and (b) 3.5 fs driving pulses obtained at the same intensity; (c) Raw images of harmonic spectra from Mn plasma at different pressures of neon in the hollow fiber obtained at the same energy of driving laser pulses [25].
31st harmonic. Only two weak neighboring harmonics (around the strong emission) are seen in the 30 - 65 eV spectral range. The ratio between the intensities of the enhanced harmonic to the weak neighboring harmonics exceeded one order of magnitude. One can note that, at a lower intensity of the femtosecond pulse (<2 × 1014 W cm−2), this strong harmonic disappeared when using both multiand few-cycle pulses.
The distinctive structure of the harmonic spectra, both for 40 fs and 3.5 fs pulses, clearly points out the involvement of Mn resonances centered around 50 - 51 eV. The same can be said about the photoionization or photoabsorption characteristics of Mn+ plasma, which are due to the “giant” 3p → 3d resonance [28]. The laser polarization dependence of this emission was analyzed and it was found that the 50 eV radiation abruptly decreases with the change of the polarization state of the femtosecond driving pulses from linear to elliptical, which is a clear signature of the emission being due to high-order harmonic generation.
To analyze the effect of the spectro-temporal characteristics of the femtosecond radiation on the harmonic yield, the pressure of neon in the hollow fiber of second compressor of laser was varied, thus changing the duration of driving pulse. The spectral and intensity variations of manganese harmonic spectra in the range of 22 - 62 eV as the functions of neon pressure in the hollow fiber are shown in Figure 7(c). One can clearly see that, with change of pressure (from 1 to 2.3 bar), the single 31st harmonic intensity varies from almost zero to its maximum high value. A blue shift of the harmonics is also evident. Further increase of neon pressure up to 3 bar, at which the experiments with the 3.5 fs pulses were carried out, did not change the harmonic distribution.
The experiments described above were carried out without carrier envelope phase (CEP) stabilization (that is, for random CEP values). The HHG experiments with Mn plasma using 3.5 fs pulses were also performed with stabilized CEP (e.g. at phases values of φ = 0 and π/2) and no considerable differences were found in that case (Figure 8), though some variation of harmonic distribution was observed for the lower order harmonics (compare the middle and bottom curves of Figure 8). The spectral shapes of the 31st harmonic emission were quite similar for these two fixed values of CEP, while a considerable difference in harmonic spectra was maintained when comparing to longer pulse duration and lower intensity of the driving pulses. Figure 8 shows HHG spectra for 25 fs pulses (upper panel) and 3.5 fs pulses (middle and bottom panels) of the same energy. One can clearly see the absence of harmonic extension and resonance-induced HHG in the case of low-intensity, 25 fs pulses.
The fact that a strong CEP dependence of the plasma-
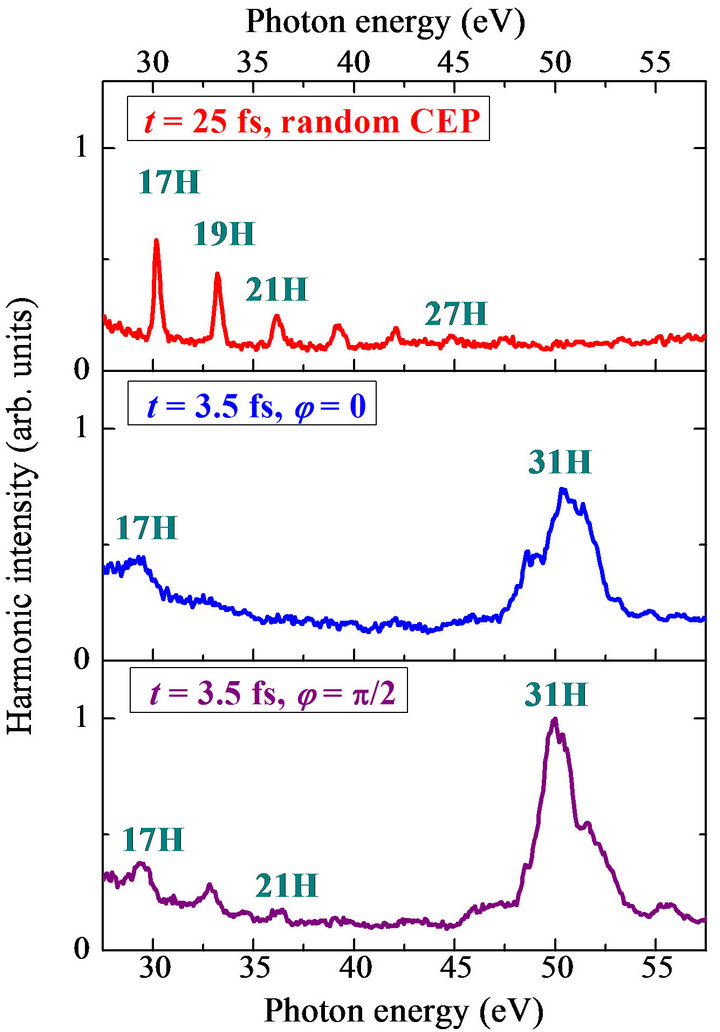
Figure 8. Experimental harmonic spectra generated from manganese plasma in the case of the absence of gas in the hollow fiber compressor (t = 25 fs) and random CEP (upper panel), and at 3 bar pressure (t = 3.5 fs) at fixed CEP (φ = 0, middle panel; φ = π/2, bottom panel). φ denotes the carrier envelope phase [25].
harmonic spectra in the case of 3.5 fs pulses was not observed could also be attributed to the presence of a significant amount of free electrons in the manganese plasma, which might diminish the difference between the HHG spectra recorded for different values of CEP. The same can be said about other HHG experiments using silver and brass plasmas, which did not show significant differences in harmonic spectra when comparing fewcycle pulses with fixed and random CEP. In the meantime, comparative studies with gas media under similar experimental conditions were carried out and found a characteristic dependence of the HHG spectra on the CEP, which were commonly observed at such conditions. Thus the absence of the influence of the CEP on the harmonic pattern generated by few-cycle pulses from the ablation plumes appears to be a specific feature of plasma HHG.
Summarizing this section, the observation of harmonic spectra from manganese plasmas driven by 3.5 fs pulses, which are dominated by a single enhanced 31st harmonic at around 50 eV, was discussed. The spectro-temporal experiments reveal the influence of the drive pulse duration on this process. Analysis of the harmonic energy tuning upon the variation of driving laser pulse duration controlled by change of gas pressure in the hollow fiber compression system show stabilization of the enhanced harmonic’s energy and wavelength, which can be explained with resonance-induced enhancement at 51 eV. The modeling of this process suggested that the emission could constitute an isolated sub-femtosecond pulse. The observed weak CEP dependence might reduce the requirements for CEP stabilization of the laser. The isolation of a single harmonic without any filtering could also be useful for various applications where the ultrashort XUV pulses are required, without the losses induced by spectral dispersion or filtering.
4. Stable Generation of High-Order Harmonics of Femtosecond Laser Radiation from Laser Produced Plasma Plumes at 1 kHz Pulse Repetition Rate
Almost all HHG studies from weakly ionized plasmas produced during laser ablation of various solid targets were carried out using the 10 Hz pulse repetition rate lasers [11]. Up to now only few studies of HHG from plasmas have been carried out on static targets using 1 kHz class lasers [33-35]. The ablation process at 1 kHz pulse repetition rate causes a considerable change of the surface properties of the target due to the melting, which deteriorates the plasma plume conditions during laser ablation. Surface heating and melting of a static target result in an unstable harmonic signal so that movement of the target surface is required to maintain a reasonable stability. The demand in finding the optimal way for improving the plasma harmonic stability at 1 kHz pulse repetition rate is high due to recent observations of the advanced properties of plasma harmonics over gas harmonics [36-38]. In particular, in [36], the plasma HHG conversion efficiency was measured one order of magnitude stronger compared with gas HHG efficiency. Analogous features were reported in [38].
The obstacle of all plasma harmonic experiments during earlier studies was an insufficient stability of plasma parameters (density, ion and free electron concentrations, excitation conditions, etc.), which led to an instability of harmonic yield and fast decay of harmonic efficiency during irradiation of the same spot of ablating target. As it was mentioned, most of those early studies were performed using a 10 Hz class lasers. At this relatively low pulse repetition rate, the stability of harmonics deteriorated after a few hundred shots on the same spot of the surface and even quicker for powder-like materials (fullerenes, nanotubes, metal nanoparticles, various organic and non-organic powders). One can note that laser ablation of the latter samples can be considered as an important tool for their structural studies using XUV nonlinear spectroscopy. The application of soft ablation allows the use of the same target for a much longer period than in the case of earlier studies of over-excited targets during laser ablation. Thus a search of a robust, easy-to-apply method for improving the harmonic stability in the case of plasma HHG could considerably advance a search of the fundamental (structural, orientational, etc.) properties of organic and inorganic atoms and molecules.
The earlier used approaches of a rotating disc geometry [39,40] for the movement of targets during ablation are not suitable since the distance between driving femtosecond beam and target surface should be maintained minimal (of order of 100 mm), while the Rayleigh length of the driving beam is maintained at the range of a few mm. Below we discuss a new method using a motorized rotating rod specifically prepared for the HHG from plasma plumes using high pulse repetition rate lasers, and demonstrate that this target significantly improves the stability of high-order harmonics [16].
Those studies were performed using two laser pulses: one to produce the plasma plume and the second to drive the HHG within it. The first (heating) pulse was created by splitting off a portion (200 μJ) of the uncompressed 8 ps laser pulse from a 1 kHz Ti: sapphire chirped pulse amplification laser. The remaining pulse was compressed in a prism compressor and then further compressed using a hollow core fibre and chirped mirrors, resulting in 250 μJ, 3.5 fs pulses. The driving pulse was delayed with respect to the heating pulse by 40 ns to give the plasma the time to expand away from the target surface to allow the driving pulse to pass through the plasma without being clipped by the target.
Target rotation and movement apparatus consisted of three linear stages driven by stepper motors along three axes. The target was attached to an axis of the fourth motor, which provided rotation with a variable speed (from a few rotations per minute (rpm) up to 300 rpm). Rotating the target was sufficient to achieve stable harmonic radiation and an additional vertical movement was not required, though this capability might be useful for future plasma HHG experiments. As the setup requires the target to be positioned very close to the driving beam, it was of paramount importance that the target was carefully aligned to the axis of rotation. Any movement of the target surface due to eccentricity in the radial direction from the driving beam axis would result in an oscillation of the harmonic signal due to variation of the plasma density seen by the driving beam or, in the extreme case, clipping of the laser beam.
The target (cylindrical rode with diameter of 10 mm and length of 30 mm) was positioned as shown in Figure 9, with the driving pulse propagating ~100 μm above the target surface. The picosecond heating pulse was focused onto the surface of the rotating target. In order to efficiently produce high-order harmonics the plasma must be weakly ionized. To achieve this the target was positioned slightly in front of the focus of the heating pulse using a 50 cm focusing lens, leading to an on target intensity of ~ 1×1010 W∙cm−2. This also had the benefit of increasing the size of the plasma produced from ablating a larger area. The size of the focus at the target surface was measured to be ≈500 μm. The delayed driving pulse was focused through the plasma using a 40 cm spherical mirror. The HHG radiation was analyzed by an XUV spectrometer consisting of a flat-field grating and an imaging microchannel plate detector with phosphor screen imaged onto a CCD camera.
Figure 10 shows that there is a drastic change in the harmonic signal (integrated over the spectral range of 40 - 80 nm) when the rotation of the aluminum target is stopped. There is a sharp intensity decrease of more than one order of magnitude over only one thousand shots (or just after one second of ablation using 1 kHz laser). The benefits of the rotating rod are clearly shown in Figure 11 where stable harmonic generation was achieved from
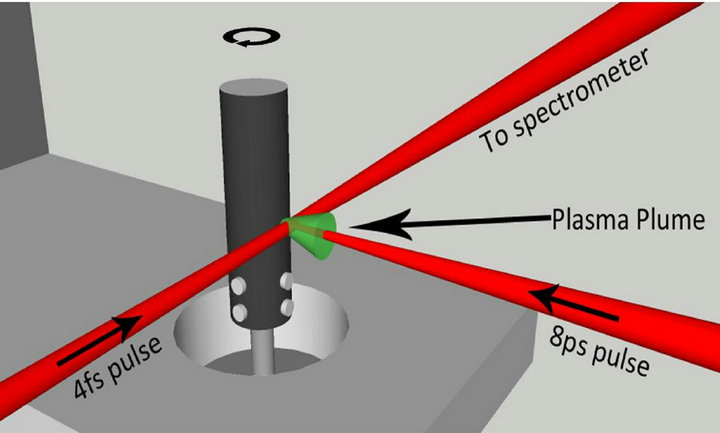
Figure 9. Schematic of rotating target and HHG configuration [16].
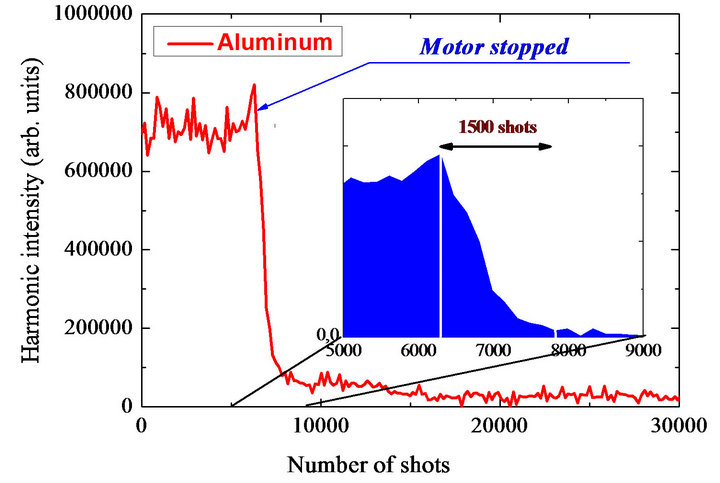
Figure 10. Decay of harmonics from aluminum plasma after stopping the rotation of the motor. The harmonics were integrated over 40 - 80 nm spectral range [16].
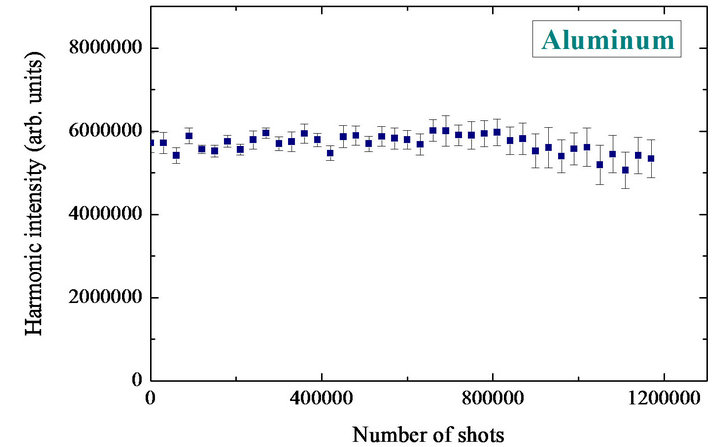
Figure 11. Stability of integrated harmonic signal from aluminum plasma in the case of rotating target [16].
the plasma produced on an aluminum target for over 1 million laser shots. Stable harmonics were achieved in a broad range of the speeds of rotation. The target rotational speed and the size of the ablation focus imply that the same area of target was undoubtedly used repeatedly for consecutive rotations over the 20 minute duration of experiments.
It is possible that once the fixed surface is melted the force from a following laser shot and plasma creation could expel some of the liquid target from the ablation area, which would not cause the plasma to be emitted in a direction normal to the surface. These effects are considerably diminished once the target starts to rotate. During rotation, the previously ablated area cools down such that, during the next set of ablation on this spot, the plasma formation occurs at approximately same conditions. To prove that the ablated area cools down with rotation, the target was rotated at different speeds (from 10 to 300 rpm) and no difference in stability of harmonic yield was found. These observations point out the importance of the periodic change of the ablation zone. This also confirms a suggestion that the cooling of the ablation area leads to stable plasma generation.
Characteristics of plasma (density and ionization state) are the most important parameters to achieve and maintain stable HHG efficiency during an extended period of target illumination. The calculations [38] have shown that, in the case of carbon plasma, the concentration of particles in the area of femtosecond laser-plasma interaction at optimal delay between heating and driving pulses (~40 ns) is ~2 ´ 1018 cm−3. The solid surface was considered as the one unheated before the laser ablation. Indeed, after one round of rotation (e.g., after 0.2 - 2 s), the plasma disappears, the ablated spot cools down, and the next laser shot on the same spot can be considered as a shot on the almost “fresh” surface. Contrary, in the case of a stationary target, the following shots continue the heating of the same spot.
Summarizing, the novelty of this approach includes the observation of advanced properties of plasma HHG even at extremely small energies of the heating pulses. The efficiency of plasma HHG depends on the possibility to create “optimal” plasma. This can be done using both multi-mJ pulses, as was shown in previous studies [38], and few hundred mJ pulses, as it was demonstrated in the reviewed work [16] and recently published studies [36]. The important point here is the intensity and fluence of the heating pulse on the target surface. The application of a higher energy heating pulse could create the conditions of “optimal” plasma over a longer distance, which could (or could not) increase the harmonic yield depending on the phase relations between the driving and harmonic waves. In addition, it can also lead to the over-heating of the target at 1 kHz ablation. As it was already mentioned above, the rotating speed did not influence the stability of harmonics using 0.2 mJ heating pulses. The use of more energetic pulses at high repetition rate (i.e. of order of few mJ) may require additional optimization of the rotation target technique (for example, by periodic up and down dragging of the rotating target).
5. High-Order Harmonic Generation in Fullerenes Using Fewand Multi-Cycle Pulses of Different Wavelengths
Finding new approaches to improve the efficiency of HHG of laser radiation towards the XUV range is an important goal of nonlinear optics and laser physics. Small sized nanostructures are an attractive approach, since they exhibit local-field-induced enhancement of the nonlinear optical response of the medium [41-43]. Another mechanism that can enhance harmonic efficiency of clusters is the increase of the recombination cross section of accelerated electron and parent particle in the final step of the three-step mechanism of HHG [44]. It was shown in [45] that laser-irradiated cluster-contained plasmas can emit low-order harmonics efficiently. The advantages of highly efficient harmonic generation in laser-produced plasmas containing nanoparticles have been analyzed in [43]. In this connection small-sized clusters, such as fullerenes, could show the advanced nonlinear optical properties Fullerenes are an attractive nonlinear medium for the HHG. Their sizes and broadband surface plasmon resonance (SPR) in the XUV range allowed the first demonstration of enhanced HHG near the SPR of C60 (λSPR » 60 nm, with 10 nm full width at half maximum) [46]. Theoretical studies of HHG from C60 using multi-cycle pulses include an extension of three-step model [47], analysis of the electron bound within a thin shell of a rigid spherical surface, with geometrical parameters similar to those of the C60 [48], and application of dynamical simulations [49]. Those studies reveal how HHG can be used to probe the electronic and molecular structure of C60. Theoretical investigation of such systems is hampered by the fact that the Hamiltonian of HHG is time dependent and the systems consist of many electrons. The investigation of the influence of the electrons on the resonant HHG can be performed by means of a multiconfigurational time-dependent Hartree-Fock (MCTDHF) approach, which has the accuracy of direct numerical solution of the Schrödinger equation and is not significantly more complicated than the ordinary time-dependent Hartree-Fock approach [7]. In particular, the computations could be based on the multiconfigurational time-dependent Hartree software packages [50]. In [7], simulations of resonant HHG were performed by means of a MCTDHF approach for three-dimensional fullerenelike systems. The influence of the SPR of C60 on the harmonic efficiency in the range of 60 nm (E = 20 eV) was analyzed and showed the role of resonant effects in the HHG enhancement.
The ionization saturation intensities of different charge states of C60 are higher compared to isolated atoms of similar ionization potential [51]. With this perspective, it is interesting to analyze HHG from fullerene molecules in the field of few-cycle laser pulses and compare these studies with those carried out using multi-cycle pulses. The motivation for the discussed studies was to analyze the conditions for efficient HHG from plasmas containing C60, using picosecond laser pulses to ablate the fullerene-containing target at high pulse repetition rate (1 kHz) and then few-cycle laser pulses (t = 3.5 fs) to generate the harmonics in the fullerene plasma [52]. We also analyze HHG in fullerenes using 1300 nm radiation and compare these studies with those using 780 nm multicycle pulses.
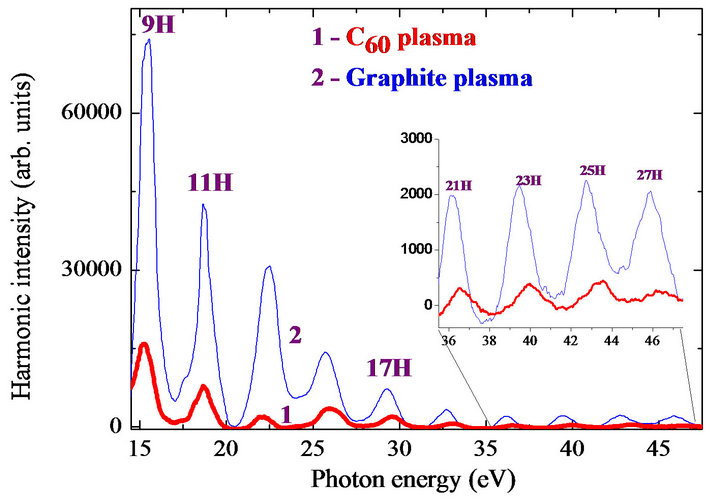
The experimental setup using a few-cycle pulses for fullerene harmonic generation was analogous to those presented in sections 3 and 4. Two types of targets were investigated: 1) C60 powder, which was glued onto a glass substrate or onto a rotating aluminum rod; and 2) bulk graphite for plasma harmonic generation. The maximum harmonic conversion efficiency was obtained by varying the distance between the femtosecond beam and the target, as well as the z-position of the plasma. The harmonic spectra from plasmas produced on the bulk graphite and fullerene powder glued onto the glass surface are presented in Figure 12(a) in the case of laser wavelength λ = 780 nm. Harmonics up to the 29th order were obtained from the fullerene plasma. The harmonic efficiency in the case of the graphite plasma was about five times higher compared with the case of fullerene plasmas, most likely due to the higher concentration of emitters in the former case, as has also been reported in [37].
The results of comparative studies of the HHG in fullerene plasma using few-cycle (3.5 fs) and multi-cycle (40 fs) pulses are shown in Figure 12(b). In the latter case, a 1 kHz repetition rate Ti:sapphire laser generating 4 mJ, 40 fs pulses was used. The HHG conversion efficiency for the 40 fs pulses at the beginning of plateau range in the case of the plasma plume containing fullerenes was estimated to be ~5 × 10−6 using a comparison with the HHG conversion efficiency in a silver plasma, which has previously been reported at similar experimental conditions to be 1 × 10−5 [43]. One can note that the cutoff in the case of longer pulses (25th harmonic) was shorter with regard to the few-cycle pulses at similar intensities of these pulses in the plasma plume.
The problem with using a fullerene powder-containing target is the shot-to-shot instability and rapid decrease of the harmonic yield, due to the abrupt change in the target
 (a)
(a)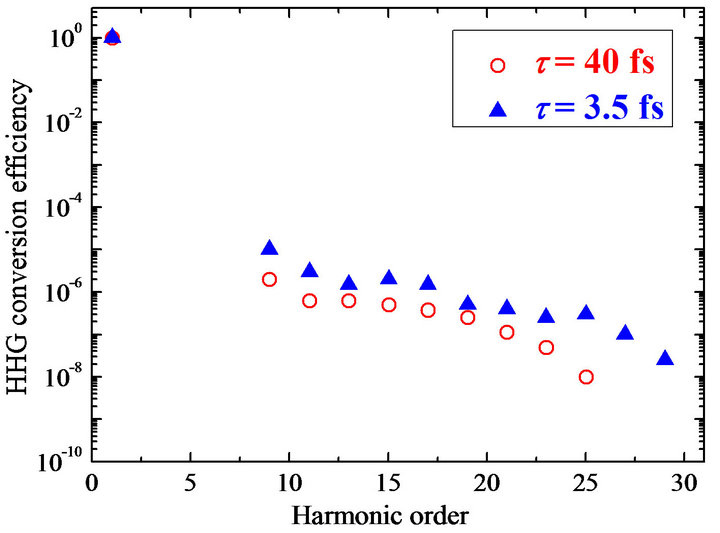 (b)
(b)
Figure 12. (a) Harmonic spectra from fullerene (thick curve) and graphite (thin curve) plasmas using the 8 ps heating pulses and 3.5 fs driving pulses at identical experimental conditions; (b) Comparison of HHG conversion efficiencies from fullerene plasma using the 3.5 fs (triangles) and 40 fs (circles) driving pulses. The laser wavelength is λ= 780 nm [52].
morphology following ablation. Such instabilities limit applications of this radiation source and greatly hamper efforts to measure the pulse duration of the harmonic emission, which typically requires a large number of laser shots. A solution to this problem might be the use of long homogeneous tapes containing fullerenes, which continuously move from shot to shot to provide a fresh surface for each next laser pulse. The use of rotating targets containing C60 is another method for improvement of the harmonic stability ([16], see also previous section) from this medium, which was implemented in the discussed work. The 15 mm diameter aluminum rods were used as the substrates onto which the fullerene powder was glued. These rotating targets considerably improved the stability of harmonics from C60-containing plasmas compared with fixed targets fabricated by gluing fullerene powder to a glass substrate. Once the target rotation is stopped, the harmonic efficiency from the fullerene plasma decreased to the noise level within 1 - 2 seconds.
This target fabrication method could be very useful in the case of powder-like targets (fullerenes, metal nanoparticles, organic powder-like samples, etc.). Previously, even at 10 Hz pulse repetition rate, the ablation of powdered targets that were not moved led to their rapid degradation and abrupt decrease of harmonic yield [43]. With this new technique, one can glue the powdered material onto the rotating rod to improve the stability of the harmonic emission. At the same time, one can note that the stability of harmonics from such powder-like targets is still worse than from rotating bulk metal rods due to the faster degradation of the target surface in the former case.
Due to small concentration of fullerenes in the plasma plume, the amount of ablated material was insignificant even at 1 kHz pulse repetition rate. So the main difference between the rotating and non-rotating targets was related with the thermal conditions of heating spot. In the case of fixed target, the melting bath appeared after 1000 shots (e.g. 1 sec of ablation), which considerably worsened the process of plasma formation. Once the target started to move, the previously heated area cooled down and again could be used for efficient ablation and harmonic generation. This phenomenon was observed from many targets. It is possible to improve the stability of harmonics (and correspondingly stability of plasma formation conditions) not just by using the fresh (non-ablated) surface but by changing the conditions of overheating of the same spot of the target.
Conversion efficiency studies in these two plasmas showed advantages of HHG in the case of graphite plasmas compared with fullerene plasmas [37]. This can be explained by the higher particle density in the graphite plasma. The concentration of fullerenes is below 1017 cm−3 [46], while density estimates for carbon plasmas based on a three-dimensional molecular dynamical simulation of laser ablation of graphite using the molecular dynamics code ITAP IMD [53] showed that for heating by 8 ps laser pulses the graphite plasma density can reach 2.6 × 1017 cm−3 at the ablation intensity of 2×1010 W∙cm−2. Another reason for the observed superior features of graphite plasma harmonics could be the production of clusters during laser ablation, though their involvement in HHG requires additional studies, including time-of-flight measurements.
In order to analyze the harmonic yield from the fullerene plasma using the mid infrared (MIR) laser source, an optical parametric oscillator (OPA) pumped by the 40 fs Ti:sapphire laser was used. A beam splitter inserted before the laser compressor of this Ti:sapphire laser was used to pick off 10% of the beam (780 nm, 1 mJ, 160 ps, 1 kHz pulses) to generate a fullerene-containing plasma plume, with the remaining 90% being compressed to 40 fs (7 mJ) to pump a computer-controlled OPA. The OPA was optimized for high conversion efficiency, beam quality and short duration of the converted pulses. The OPA provided signal pulses with duration of 35 fs in the 1200 - 1600 nm spectral range with a maximum energy of 1.7 mJ at ~1300 nm. The idler pulses covered the 1600 - 2200 nm range with a maximum energy of 1 mJ at ~ 2000 nm. The delay between the heating ablation pulse and MIR pulse from the OPA was set to 35 ns, as this delay was found to be optimal for the efficient generation of extended harmonics from fullerene plasma.
Figure 13 shows the comparison of fullerene harmonic spectra generated in the case of 1300 and 780 nm multi-cycle pulses. Harmonics up to the 41st order (Figure 13, bottom panel) were observed in the case of 1300 nm pulses at the conditions of optimal plasma formation using the heating 160 ps pulses. The application of less intense, longer wavelength (1400 nm) pulses available by tuning the OPA did not result in an extension of harmonic cut-off compared with the case of 1300 nm pulses. This observation suggests that the harmonic generation occurred under saturated conditions, with the expectation of stronger harmonics once the microand macro-processes governing frequency conversion are optimized. Over-excitation of target by 160 ps pulses (Figure 13, middle panel) led to appearance of plasma emission in the 25 - 45 eV range of photon energies (λ = 27 - 50 nm). At these conditions, no harmonics were observed during propagation of femtosecond pulses through such overexcited plasma.
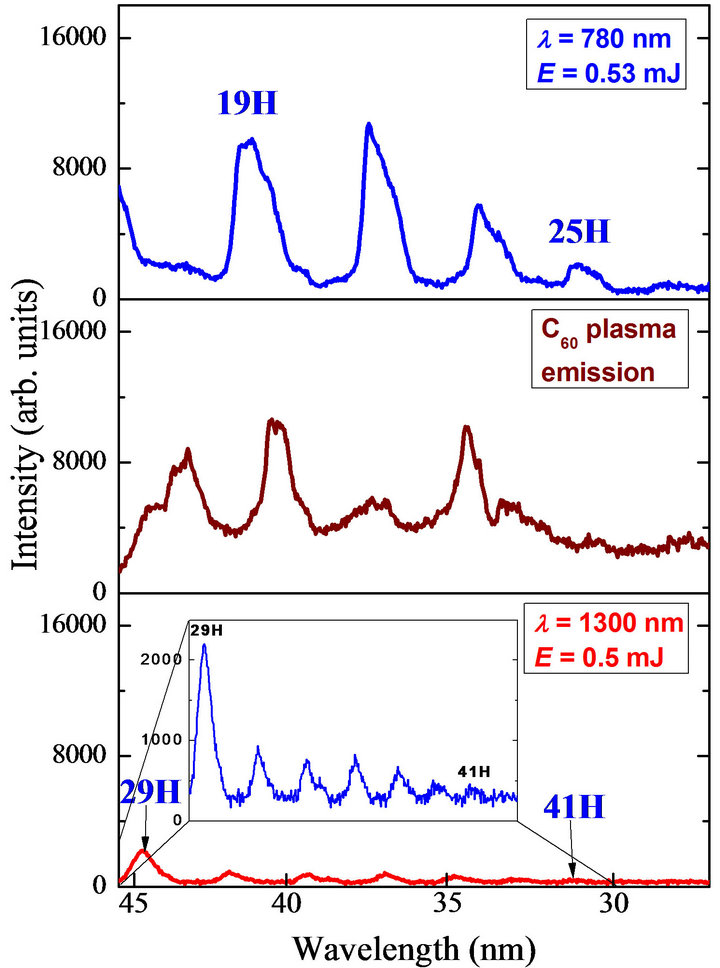
Figure 13. Comparative harmonic spectra from fullerenecontained plume using the 780 nm (upper panel) and 1300 nm (bottom panel) multi-cycle pulses (intensity of 160 ps heating pulses Ips = 1 × 1010 W∙cm−2). The intensity axes are on the same scale allowing a direct comparison between the three cases. The middle panel shows C60 plasma emission spectrum at over-excitation of target by 160 ps heating pulses (Ips = 4 × 1010 W∙cm−2), without further excitation by femtosecond driving pulses [52].
The harmonic spectrum up to the 25th order in the case of 780 nm, 40 fs pulses is presented in the Figure 13 (upper panel). One can clearly see the extension of harmonic cut-off (from the point of view of highest harmonic order) in the case of longer-wavelength driving pulses by comparing the HHG spectra using the 780 and 1300 nm pulses, while the extension of cut-off energy was insignificant.
Approximately equal energies of driving pulses were maintained in these cases (0.53 mJ for 780 nm pulses and 0.5 mJ for 1300 nm pulses). The intensity of 780 nm radiation in the plasma area was calculated to be Ifs = 4 × 1014 W∙cm−2. The pulse durations of these sources (780 and 1300 nm) were approximately same (40 and 35 fs respectively). Probably due to phase modulation and propagation through multiple optical elements in optical parametric oscillator-amplifier, the diameter of 1300 nm beam in the plasma plume was larger than in the case of 780 nm beam. The corresponding lower intensity of 1300 nm radiation could be responsible for less expected extension of harmonic cut-off energy. From the cut-off formula, one could expect the generation of harmonics up to the 47th order (in the case of 780 nm radiation), well above the observed cut-off (25th harmonic), which probably points out the difference in expected and actual intensity in the plasma area at the optimal conditions of HHG. The reason in this discrepancy could be related with the self-defocusing of driving pulses in the medium containing free electrons.
In atoms the maximum emitted photon energy (giving the cut-off position) is described by the well known relation EM = I + 3.17Up with I the ionization energy and Up the ponderomotive energy. By invoking the three step model [44] this formula can be derived under the assumptions that the laser field amplitude is constant. Rapidly varying laser pulses can considerably shift the cutoff [54,55]. The molecules support more returning trajectories than atoms and allow the existence of several plateau [56]. It is not therefore easy to disentangle the effects of pulse shape and presence of a molecule and to state a general law for the position of the cutoff; the EM = I + 3.17Up law can therefore be used only as a touchstone.
It was observed that the plasma harmonic yields from the 780 and MIR probe pulses are consistent with the predicted single-atom harmonic intensity wavelength scaling Ih µ λ−5, which arises due to electron wavepacket spreading before recollision [57,58]. The harmonic efficiency of the XUV radiation in the range of 30 - 50 nm driven by MIR pulses was 7 to 15 times less compared with the case of 780 nm probe pulses, which is comparable with the expected ratio between harmonic intensities from these sources ((1300/780)5 » 12.7) followed from above rule, assuming approximately equal energies of the 780 and 1300 nm pulses (0.53 and 0.5 mJ respectively).
The fact that HHG in the fullerene system exhibits a wavelength scaling that is consistent with single-atom predictions allowed to employ a theoretical model [59] in which the interaction of short pulses with C60 was treated in the single active electron approximation with one electron constrained over a structureless spherical surface of radius R = 3.55 × 10−8 cm = 6.71a0. This simplified model can be treated in an analytical fashion. It permits a physical understanding of the dynamics of the active electron, and allows an easy check of resonances between bare molecular state. Indeed a generalization of the model can be used to analyze the physical properties, the energy content and stability of hollow spherical clusters [60]. The calculated harmonic spectra from C60 are presented in Figure 14 in the case of 780 nm (photon energy Eph = 1.6 eV) and 1300 nm (photon energy Eph = 0.96 eV) pulses propagating through the fullerene medium. The
 (a)
(a)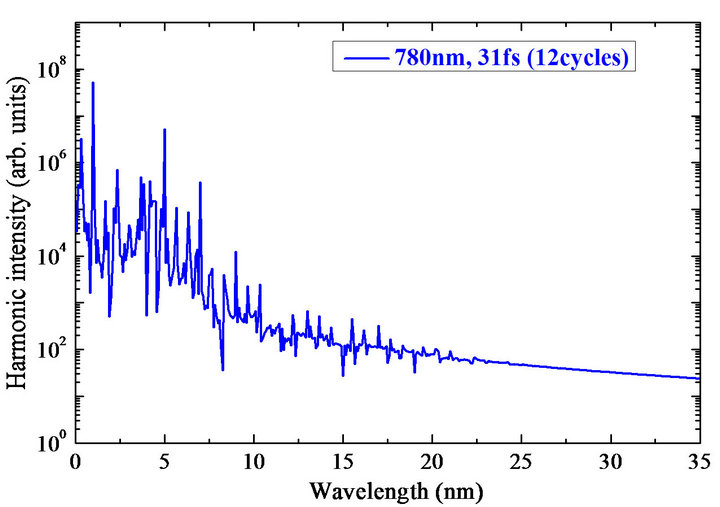 (b)
(b)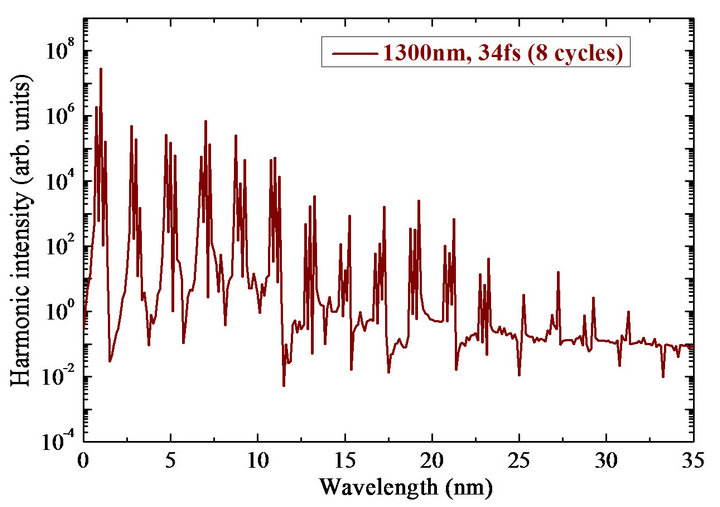 (c)
(c)
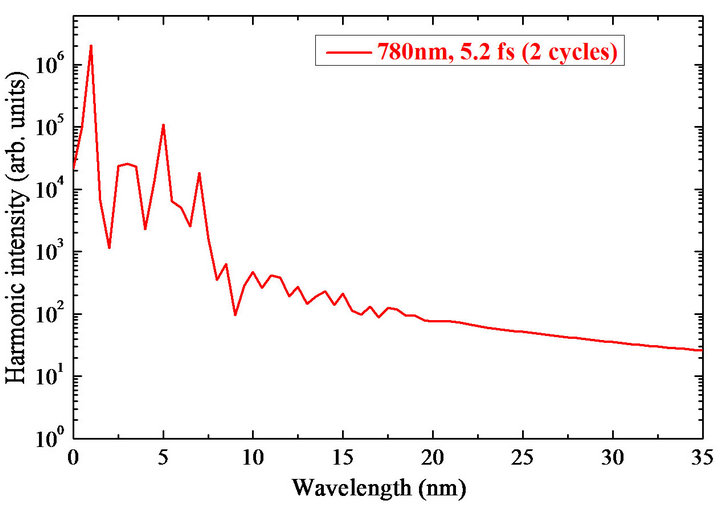
Figure 14. Calculated data of the harmonic spectra from fullerene plasma in the case of (a,b) 780 nm and (c) 1300 nm driving radiation. The pulse durations are (a) 2 optical cycles (5.2 fs), (b) 12 optical cycles (31 fs) and (c) 8 optical cycles (34 fs) [52].
calculations were carried out for 2-cycle pulses (t = 5.2 fs) and 12-cycle pulses (t = 31 fs) of 780 nm radiation and 8- cycle pulses (t = 34 fs) of 1300 nm radiation and intensity 6 × 1014 W∙cm−2, which were close to the conditions of fullerene HHG experiments.
The spectra of well-resolved harmonics were obtained but with broadened lines (in the case of short pulses) and hyper Raman lines (in the case of long pulses). Hyper Raman lines with frequency other than harmonics, are due to transitions between laser dressed molecular states [61,62]. The presence of these lines has been predicted since the very beginning of the theoretical treatment of HHG [63] and found in different contexts such as twolevel approximation, quantum dots calculations, hydrogen atom and so on [64-67] but never observed in actual experiments. Several explanations have been proposed to explain this failure; for example it has been argued that they add destructively in the forward direction or that they show a transient nature and are thus overwhelmed by the presented odd harmonics [68,69].
The calculations [52] showed well-defined harmonics (up to Hc = 31) in the case of 1300 nm multi-cycle pulses. The theoretical model exploited the spherical symmetry of the C60 by introducing a number of approximations, the most important of which is that the molecule cannot be ionized. This approximation deserves some comment. In spite of the ionization suppression of the C60 molecule, some ionization is bound to occur so that the theory becomes unreliable when ionization becomes significant. The harmonic cut-off in the case of 1300 nm radiation was extended compared with 780 nm radiation (Hc = 17), analogously as in the case of experiment.
Previous HHG studies in fullerenes were performed using the multi-cycle pulses (30 fs, 48 fs, and 110 fs [43]). The stability of C60 against fragmentation in multicycle laser fields leads to fast diffusion of the excitation energy. Even better conditions can occur in the case of few-cycle pulses used for fullerene HHG. In that case fullerenes can withstand the influence of the strong field of few-cycle pulses due to the increase of the ionization saturation intensity as the pulse duration is decreased. This can further increase the diffusion of the excitation energy within the fullerenes due to their very large number of internal degrees of freedom. The increase of energy diffusion is expected to lead to a decrease in the disintegration of fullerenes, which enhances the probability of harmonic emission from these molecules.
The graphite plasma, which was compared in these experiments with C60, can be easily aggregated during laser ablation, thus leading to nanoparticles formation in the laser plume, as it was shown in [36-38]. In that case the comparison of two clustered species (large 5 - 20 nm carbon clusters and 0.7 nm C60) can lead to their different nonlinear optical response once the interacting laser pulse becomes compressed from the multi-cycle to fewcycle duration. The discussed results show that for the shortest laser pulses, the HHG cut-off for fullerene is extended, while the harmonic intensity is reduced compared with “carbon harmonics”. The intensity of the femtosecond pulse is an important parameter in for optimizing the HHG from C60. Increasing the intensity of the driving pulse did not lead to an extension of the harmonic cutoff from the fullerene plume, which is a signature of HHG saturation in the medium. Moreover, at relatively high intensities, a decrease in the harmonic output was observed, which can be attributed to the phase mismatch caused by propagation effects.
The stability of C60 molecules against ionization and fragmentation is of particular importance, especially for their application as a medium for HHG using laser pulses of different duration. The fullerene molecules ablated off the surface should be intact when the driving pulse arrives. Hence, the heating pulse intensity also becomes a sensitive parameter. At lower intensities of heating pulse, the concentration of the clusters in the plume would be low, while at higher intensities one can expect fragmentation. This phenomenon is observed when the heating pulse intensity on the surface of fullerene-rich targets is increased above the critical value (Figure 13, middle panel). The abrupt reduction in harmonic intensity in that case can be attributed to phenomena such as fragmentation of fullerenes, an increase in free electron density, and self-defocusing of the driving pulse, all of which are expected to reduce the efficiency of HHG.
Summarizing this section, the experimental and theoretical studies of high-order harmonic generation in the plasmas containing fullerenes (up to the 29th and 41st orders for the 780 and 1300 nm radiation) under different plasma conditions and laser parameters in the case of fewand multi-cycle pulses show the attractiveness of applications of this medium for frequency conversion of laser radiation. The comparison of harmonics from C60-rich plasmas and plasmas produced on graphite surface showed stronger harmonic yield in the latter case, which was attributed to higher density of the plasma plume and the formation of clusters during the ablation of graphite targets. The experiments with fullerene powder glued onto aluminum rotating rods demonstrated a dramatic improvement in harmonic generation stability compared with static fullerene-containing targets. The comparative studies using 3.5 and 40 fs pulses showed that, for few-cycle pulses, the harmonic cutoff is extended compared with multi-cycle pulses, which can be attributed to reduced fragmentation of C60 for the shorter pulse. The comparison of fullerene harmonic spectra generated in the case of 1300 and 780 nm multi-cycle pulses showed the extension of generating harmonic orders in the former case. The plasma harmonic yield approximately follows the Ih µ λ−5 wavelength scaling rule predicted for single atoms. The maximal conversion efficiency obtained in these fullerene HHG studies was estimated to be 5 × 10−6. Theoretical calculations of fullerene harmonic spectra were carried out in the single active electron approximation, which showed harmonics up to Hc = 31 in the case of 1300 nm multi-cycle pulses and up to Hc = 17 in the case of 780 nm multi-cycle pulses.
6. Perspectives of Plasma HHG
The quest for new plasma media that would favor the enhancement of an individual harmonic allows further enhancement of harmonic conversion efficiency. The production of a single high-intensity harmonic (rather than a group of harmonics of equal intensity in the plateau region) would open up the way to the practical application of these coherent short-wavelength radiation sources. Because resonantly enhanced harmonics have already been observed in several plasma media, there are strong grounds to believe that similar conditions will be discovered for other plasma formations. The generated harmonic wavelength may then be tuned to the transitions with high oscillator strength by wavelength tuning of the driving laser system, as well as by varying the chirp of the laser radiation. Application of ablated nanoparticles and clusters for HHG can also enhance the yield of harmonics in the XUV range. Further improvements in HHG conversion efficiency and harmonic extension require a systematic study of the influence of various plasma and laser parameters on ablation harmonics. Many new peculiarities of plasma harmonics emerged during last few years allow expecting further extension of our knowledge of materials properties using this powerful tool of nonlinear spectroscopy.
Whilst the first stage of these successful studies was entirely focused on the improvements of harmonic yield from plasma, at current stage of knowledge of the high-order nonlinear optical processes in ablation plume one can consider this method as a new technique for materials science. Thus the search of the dual role of plasma HHG as a method for efficient coherent XUV light generation and of materials probing is a milestone for future developments and the next stage of studies would be aimed at the enhancement of HHG efficiency from laser ablation produced on the surfaces of solid-state materials and applications of plasma harmonics for analysis of spectral and structural properties of materials.
Future studies are aimed on an analysis of the HHG spectroscopy conducted using a low-excited laser-produced plasma, which has already demonstrated several new approaches to the problem of increasing the HHG efficiency in comparison with the efficiency of conventional HHG in gases. At the same time, it is obvious that gas HHG exhibits much higher harmonic orders (in comparison with the plasma HHG obtained to date). Without making excessively optimistic predictions that the orders of in-plasma-generated harmonics will exceed the in-gas harmonic orders in the nearest future, the researchers can focus primarily on the realization of new techniques for increasing the wavelength-converted radiation intensity with the use of plasma plumes, which may hardly be realized in conventional gas HHG. At the same time, these studies will allow to explore various optical, nonlinear optical, and structural properties of materials using the laser ablation induced HHG spectroscopy.
It is worth noting that, currently, nonlinear spectroscopy involving gas HHG trying to deal with such problems as (a) extension of the HHG spectroscopy based attosecond structural imaging technique to image nuclear re-arrangements induced by localized hole excitations, (b) application of strong-field ionization to create localized hole excitations and study their attosecond dynamics in polyatomic molecules, (c) search of selective imaging of hole dynamics induced by the removal of e.g. inner-valence electrons using the XUV initiated HHG technique, and (d) development of multi-dimensional HHG spectroscopy capable of following energy flow between different molecular modes over multiple femtosecond timescale. The proposed laser ablation induced HHG spectroscopy allows adding some important impulse to those studies, by using the peculiarities of plasma HHG.
One can expect an improvement of plasma HHG due to the double excitation of laser-produced plasmas, optimization of the longitudinal harmonic generation scheme in the laser plume, optimization of nanostructured plasmas, use of multicomponent plasma plumes, formation of quasi-phase-matching conditions for the waves in complex extended plasmas, provision of a regime of waveguide pump propagation through the plasma medium, feasibility analysis of atto second pulse generation in laser-produced plasma, use of mid-IR pulses for harmonic extension, stabilization of plasmas and harmonics characteristics using rotating and moving targets, search of the attosecond pulse generation by achieving the continuum in the harmonic emission near the cut-off, which allows for the first time the generation of ultrashort laser pulses in the plasma plumes, etc. All these concepts are new and did not apply previously for the improvement of plasma harmonic generation efficiency. The joint implementation of new and old (application of the clusters with controllable and variable sizes, resonance-induced harmonic enhancement, two-color pump-induced enhancement of even harmonics, search of the influence of multi-electron dynamics of complex clusters, such as nanotubes and graphenes, on the plasmon resonanceinduced growth of few harmonics in the XUV range, etc.) methods and approaches in the case of plasma media allows making the advance to the state-of-the-art within the plasma HHG field, which will lead to the establishment of a new method of material science laser ablation induced high-order harmonic generation spectroscopy. It follows from the above that investigations in this area of nonlinear optics are making rapid strides and may bring new success in the nearest future.
7. Acknowledgements
Author thanks J. P. Marangos, A. V. Andreev, H. Kuroda, S. Y. Stremoukhov, T. Witting, C. Hutchison, F. Frank, M. Tudorovskaya, M. Lein, A. Zaïr, J. W. G. Tisch, T. Ozaki, and E. Fiordilino for fruitful discussions and collaboration.
REFERENCES
- L N. A. Papadogiannis, L. A. A. Nikolopoulos and D. Charalambidis, “Two-Photon Ionization of He through a Superposition of Higher Harmonics,” Physical Review Letters, Vol. 90, No. 13, 2003, Article ID: 133902. doi:10.1103/PhysRevLett.90.133902
- J. Itatani, J. Levesque, D. Zeidler, H. Niikura, H. Pépin, J.-C. Kieffer, P. B. Corkum and D. M. Villeneuve, “Tomographic Imaging of Molecular Orbitals,” Nature, Vol. 432, No. 7019, 2004, pp. 867-872. doi:10.1038/nature03193
- R. I. Tobey, M. E. Siemens, O. Cohen, M. M. Murnane, H. C. Kapteyn and K. A. Nelson, “Ultrafast Extreme Ultraviolet Holography: Dynamic Monitoring of Surface Deformation,” Optics Letters, Vol. 32, No. 3, 2007, pp. 286-288. doi:10.1364/OL.32.000286
- P. M. Paul, E. S. Toma, P. Breger, G. Mullot, F. Auge, P. Balcou, H. G. Muller and P. Agostini, “Observation of a Train of Attosecond Pulses from High Harmonic Generation,” Science, Vol. 292, No. 5522, 2001, pp. 1689- 1692. doi:10.1126/science.1059413
- M. Drescher, M. Hentschel, R. Kienberger, G. Tempea, C. Spielmann, G. A. Reider, P. B. Corkum and F Krausz, “X-Ray Pulses Approaching the Attosecond Frontier,” Science, Vol. 291, No. 5510, 2001, pp. 1923-1927. doi:10.1126/science.1058561
- P. B. Corkum and F. Krausz, “Attosecond Science,” Nature Physics, Vol. 3, No. 6, 2007, pp. 381-387. doi:10.1038/nphys620
- P. V. Redkin and R. A. Ganeev, “Simulation of Resonant High-Order Harmonic Generation in a Three-Dimensional Fullerenelike System by Means of a Multiconfigurational Time-Dependent Hartree-Fock Approach,” Physical Review A, Vol. 81, No. 6, 2010, Article ID: 063825. doi:10.1103/PhysRevA.81.063825
- R. A. Ganeev, H. Singhal, P. A. Naik, U. Chakravarty, V. Arora, J. A. Chakera, R. A. Khan, M. Raghuramaiah, S. R. Kumbhare, R. P. Kushwaha and P. D. Gupta, “Optimization of the High-Order Harmonics Generated from Silver Plasma,” Applied Physics B, Vol. 87, No. 2, 2007, pp. 243- 247. doi:10.1007/s00340-007-2583-0
- R. A. Ganeev, L. B. Elouga Bom, J.-C. Kieffer and T. Ozaki, “Demonstration of the 101st Harmonic Generated from a Laser-Produced Manganese Plasma,” Physical Review A, Vol. 76, No. 2, 2007, Article ID: 023831. doi:10.1103/PhysRevA.76.023831
- R. A. Ganeev, M. Baba, M. Suzuki and H. Kuroda, “High-Order Harmonic Generation from Silver Plasma,” Physics Letters A, Vol. 339, No. 1-2, 2005, pp. 103-106. doi:10.1016/j.physleta.2005.02.073
- R. A. Ganeev, “Generation of High-Order Harmonics of High-Power Lasers in Plasmas Produced Under Irradiation of Solid Target Surfaces by a Prepulse,” Physics Uspekhi, Vol. 52, No. 1, 2009, pp. 55-79. doi:10.3367/UFNe.0179.200901c.0065
- M. Suzuki, M. Baba, R. A. Ganeev, H. Kuroda and T. Ozaki, “Intense Exact Resonance Enhancement of Single-High-Harmonic from an Antimony Ion by Using Ti: Sapphire Laser at 37 nm,” Optics Express, Vol. 15, No. 3, 2007, pp.1161-1166. doi:10.1364/OE.15.001161
- A. V. Andreev, R. A. Ganeev, H. Kuroda, S. Y. Stremoukhov and O. A. Shoutova, “High-Order Harmonic Cut-Off Frequency in Atomic Silver Irradiated by Femtosecond Laser Pulses: Theory and Experiment,” European Physical Journal D, Vol. 67, No. 1, 2013, p. 22. doi:10.1140/epjd/e2012-30527-0
- A. V. Andreev, S. Y. Stremoukhov and O. A. Shoutova, “Nonlinear Optical Response of an Atom in the Field of Femtosecond Laser Pulses with Near-Atomic Intensity,” JETP Letters, Vol. 93, No. 8, 2011, pp. 476-486. doi:10.1134/S0021364011080030
- R. A. Ganeev, “High-Order Harmonic Generation in a Laser Plasma: a Review of Recent Achievements,” Journal of Physics B, Vol. 40, No. 22, 2007, pp. R213-R254. doi:10.1088/0953-4075/40/22/R01
- C. Hutchison, R. A. Ganeev, T. Witting, F. Frank, W. A. Okell, J. W. G. Tisch and J. P. Marangos, “Stable Generation of High-Order Harmonics of Femtosecond Laser Radiation from Laser Produced Plasma Plumes at 1 kHz Pulse Repetition Rate,” Optics Letters, Vol. 37, No. 11, 2012, pp. 2064-2066. doi:10.1364/OL.37.002064
- A. V. Andreev, “Interaction of an Atom with Superstrong Laser Fields,” Journal of Experimental and Theoretical Physics, Vol. 89, No. 3, 1999, pp. 421-427. doi:10.1134/1.558999
- A. D. Shiner, B. E. Schmidt, C. Trallero-Herrero, H. J. Wörner, S. Patchkovskii, P. B. Corkum, J.-C. Kieffer, F. Légaré and D. M. Villeneuve, “Probing Collective MultiElectron Dynamics in Xenon with High-Harmonic Spectroscopy,” Nature Physics, Vol. 7, No. 6, 2011, pp. 464- 467. doi:10.1038/nphys1940
- R. A. Ganeev, M. Suzuki, T. Ozaki, M. Baba and H. Kuroda, “Strong Resonance Enhancement of a Single Harmonic Generated in the Extreme Ultraviolet Range,” Optics Letters, Vol. 31, No. 11, 2006, pp. 1699-1701. doi:10.1364/OL.31.001699
- R. A. Ganeev, P. A. Naik, H. Singhal, J. A. Chakera and P. D. Gupta, “Strong Enhancement and Extinction of Single Harmonic Intensity in the Midand End-Plateau Regions of the High Harmonics Generated in Weakly Excited Laser Plasmas,” Optics Letters, Vol. 32, No. 1, 2007, pp. 65-67. doi:10.1364/OL.32.000065
- R. A. Ganeev, M. Suzuki, M. Baba and H. Kuroda, “Extended High-Order Harmonics from Laser-Produced Cd and Cr Plasmas,” Applied Physics Letters, Vol. 94, No. 5, 2009, Article ID: 051101. doi:10.1063/1.3072353
- M. Hentschel, R. Kienberger, C. Spielmann, G. A. Reider, N. Milosevic, T. Brabec, P. Corkum, U. Heinzmann, M. Drescher and F. Krausz, “Attosecond Metrology,” Nature, Vol. 414, No. 6863, 2001, pp. 509-514. doi:10.1038/35107000
- C. Altucci, J. W. G. Tisch and R. Velotta, “Single Attosecond Light Pulses from Multi-Cycle Laser Sources,” Journal of Modern Optics, Vol. 58, No. 18, 2011, pp. 1585-1610. doi:10.1080/09500340.2011.611913
- T. Witting, F. Frank, W. A. Okell, C. A. Arrell, J. P. Marangos and J. W. G. Tisch, “Sub-4-fs Laser Pulse Characterization by Spatially Resolved Spectral Shearing Interferometry and Attosecond Streaking,” Journal of Physics B, Vol. 45, No. 7, 2012, Article ID: 074014. doi:10.1088/0953-4075/45/7/074014
- R. A. Ganeev, T. Witting, C. Hutchison, F. Frank, M. Tudorovskaya, M. Lein, W. A. Okell, A. Zaïr, J. P. Marangos and J. W. G. Tisch, “Isolated sub-fs XUV Pulse Generation in Mn Plasma Ablation,” Optics Express, Vol. 20, No. 23, 2012, pp. 25239-25248. doi:10.1364/OE.20.025239
- D. Kilbane, E. T. Kennedy, J. P. Mosnier, J. T. Costello and P. van Kampen, “EUV Photoabsorption Spectra of Cd II and Cd III,” Journal of Physics B, Vol. 38, No. 1, 2005, pp. 83-88. doi:10.1088/0953-4075/38/1/008
- V. K. Dolmatov, “Characteristic Features of the 3p Absorption Spectra of Free Iron-Group Elements due to the Duplicity of the ‘Inner-Valence’ 3d Electrons. Application to Mn2+,” Journal of Physics B, Vol. 29, No. 29, 1996, pp. L687-L692. doi:10.1088/0953-4075/29/19/001
- H. Kjeldsen, F. Folkmann, B. Kristensen, J. B. West and J. E. Hansen, “Absolute Cross Section for Photoionization of Mn+ in the 3p Region,” Journal of Physics B, Vol. 37, No. 6, 2004, pp. 1321-1330. doi:10.1088/0953-4075/37/6/014
- J. B. West, J. E. Hansen, B. Kristensen, F. Folkmann and H. Kjeldsen, “Revised Interpretation of the Photoionization of Cr+ in the 3p Excitation Region,” Journal of Physics B, Vol. 36, No. 19, 2003, pp. L327-334. doi:10.1088/0953-4075/36/19/L04
- V. Strelkov, “Role of Autoionizing State in Resonant High-Order Harmonic Generation and Attosecond Pulse Production,” Physical Review Letters, Vol. 104, No. 12, 2010, Article ID: 123901. doi:10.1103/PhysRevLett.104.123901
- M. V. Frolov, N. L. Manakov and A. F. Starace, “Potential Barrier Effects in High-Order Harmonic Generation by Transition-Metal Ions,” Physical Review A, Vol. 82, No. 2, 2010, Article ID: 023424. doi:10.1103/PhysRevA.82.023424
- M. Tudorovskaya and M. Lein, “High-Order Harmonic Generation in the Presence of a Resonance,” Physical Review A, Vol. 84, No. 1, 2011, Article ID: 013430. doi:10.1103/PhysRevA.84.013430
- R. A. Ganeev, C. Hutchison, T. Siegel, M. E. López-Arias, A. Zaïr and J. P. Marangos, “High-Order Harmonic Generation from Metal Plasmas Using 1 kHz Laser Pulses,” Journal of Modern Optics, Vol. 58, No. 10, 2011, pp. 819-822. doi:10.1080/09500340.2011.581768
- R. A. Ganeev, C. Hutchison, T. Siegel, A. Zaïr and J. P. Marangos, “Quantum Path Signatures in Harmonic Spectra from Metal Plasma,” Physical Review A, Vol. 83, No. 6, 2011, Article ID: 063837. doi:10.1103/PhysRevA.83.063837
- R. A. Ganeev, C. Hutchison, A. Zaïr, T. Witting, F. Frank, W. A. Okell, J. W. G. Tisch and J. P. Marangos, “Enhancement of High Harmonics from Plasmas Using TwoColor Pump and Chirp Variation of 1 kHz Ti:sapphire Laser Pulses,” Optics Express, Vol. 20, No. 1, 2012, pp. 90-100. doi:10.1364/OE.20.000090
- L. B. Elouga Bom, S. Haessler, O. Gobert, M. Perdrix, F. Lepetit, J.-F. Hergott, B. Carré, T. Ozaki and P. Salières, “Attosecond Emission from Chromium Plasma,” Optics Express, Vol. 19, No. 4, 2011, pp. 3677-3685. doi:10.1364/OE.19.003677
- Y. Pertot, L. B. Elouga Bom, V. R. Bhardwaj and T. Ozaki, “Pencil Lead Plasma for Generating Multimicrojoule High-Order Harmonics with a Broad Spectrum,” Applied Physics Letters, Vol. 98, No. 10, 2011, p. 101104. doi.org/10.1063/1.3558999
- R. A. Ganeev, T. Witting, C. Hutchison, F. Frank, P. V. Redkin, W. A. Okell, D. Y. Lei, T. Roschuk, S. A. Maier, J. P. Marangos and J. W. G. Tisch, “Enhanced High-Order Harmonic Generation in a Carbon Ablation Plume,” Physical Review A, Vol. 85, No. 1, 2012, Article ID: 015807. doi:10.1103/PhysRevA.85.015807
- W. Theobald, C. Wulker, F. R. Schafer and B. N. Chichkov, “High-Order Harmonic Generation in Carbon Vapor and Low Charged Plasma,” Optics Communications, Vol. 120, No. 3-4, 1995, pp. 177-183. doi:10.1016/0030-4018(95)00463-I
- M. López-Arias, M. Oujja, M. Sanz, R. A. Ganeev, G. S. Boltaev, N. K. Satlikov, R. I. Tugushev, T. Usmanov and M. Castillejo, “Low-Order Harmonic Generation in Metal Ablation Plasmas in Nanosecond and Picosecond Laser Regimes,” Journal of Applied Physics, Vol. 111, No. 4, 2012, Article ID: 043111. doi:10.1063/1.3686740
- T. D. Donnelly, T. Ditmire, K. Neuman, M. D. Perry and R. W. Falcone, “High-Order Harmonic Generation in Atom Clusters,” Physical Review Letters, Vol. 76, No. 14, 1996, pp. 2472-2475. doi:10.1103/PhysRevLett.76.2472
- C. Vozzi, M. Nisoli, J.-P. Caumes, G. Sansone, S. Stagira, S. De Silvestri, M. Vecchiocattivi, D. Bassi, M. Pascolini, L. Poletto, P. Villoresi and G. Tondello, “Cluster Effects in High-Order Harmonics Generated by Ultrashort Light Pulses,” Applied Physics Letters, Vol. 86, No. 11, 2005, Article ID: 111121. doi.org/10.1063/1.1888053
- R. A. Ganeev, “Harmonic Generation in Laser-Produced Plasmas Containing Atoms, Ions and Clusters: A Review,” Journal of Modern Optics, Vol. 59, No. 5, 2012, pp. 409-439. doi:10.1080/09500340.2011.636155
- P. B. Corkum, “Plasma Perspective on Strong Field Multiphoton Ionization,” Physical Review Letters, Vol. 71, No. 13, 1993, pp. 1994-1997. doi:10.1103/PhysRevLett.71.1994
- S. V. Popruzhenko, D. F. Zaretsky and D. Bauer, “Energy Absorption and Emission of Harmonics by Clusters Subject to Intense Short Laser Pulses,” Laser Physics Letters, Vol. 5, No. 9, 2008, pp. 631-646. doi:10.1002/lapl.200810050
- R. A. Ganeev, L. B. Elouga Bom, J. Abdul-Hadi, M. C. H. Wong, J. P. Brichta, V. R. Bhardwaj and T. Ozaki, “HigherOrder Harmonic Generation from Fullerene by Means of the Plasma Harmonic Method,” Physical Review Letters, Vol. 102, No. 1, 2009, Article ID: 013903. doi:10.1103/PhysRevLett.102.013903
- M. F. Ciappina, A. Becker and A. Jaron-Becker, “Multislit Interference Patterns in High-Order Harmonic Generation in C60,” Physical Review A, Vol. 76, No. 6, 2007, Article ID: 063406. doi:10.1103/PhysRevA.76.063406
- M. Ruggenthaler, S. V. Popruzhenko and D. Bauer, “Recollision-Induced Plasmon Excitation in Strong Laser Fields,” Physical Review A, Vol. 78, No. 3, 2008, Article ID: 033413. doi:10.1103/PhysRevA.78.033413
- G. P. Zhang, “Optical High Harmonic Generation in C60,” Physical Review Letters, Vol. 95, No. 4, 2005, Article ID: 047401. doi:10.1103/PhysRevLett.95.047401
- H.-D. Meyer, U. Manthe and L. S. Cederbaum, “The Multi-Configurational Time-Dependent Hartree Approach,” Chemical Physics Letters, Vol. 165, No. 1, 1990, pp. 73-78. doi:10.1016/0009-2614(90)87014-I
- V. R. Bhardwaj, P. B. Corkum and D. M. Rayner, “Recollision during the High Laser Intensity Ionization of C60,” Physical Review Letters, Vol. 93, No. 4, 2004, Article ID: 043001. doi:10.1103/PhysRevLett.93.043001
- R. A. Ganeev, C. Hutchison, T. Witting, F. Frank, S. Weber, W. A. Okell, E. Fiordilino, D. Cricchio, F. Persico, A. Zaïr, J. W. G. Tisch and J. P. Marangos, “HighOrder Harmonic Generation in Fullerenes Using Fewand Multi-Cycle Pulses of Different Wavelengths,” Journal of the Optical Society of America B, Vol. 30, No. 1, 2013, pp. 7-12. doi:10.1364/JOSAB.30.000007
- J. Roth, F. Géahler and H.-R. Trebin, “A Molecular Dynamics, Run with 5 180 116 000 Particles,” Journal of Modern Physics C, Vol. 11, No. 2, 2000, pp. 317-322. doi:10.1142/S0129183100000298
- E. Fiordilino and V. Miceli, “Laser Pulse Shape Effects in Harmonic Generation from a Two-Level Atom,” Journal of Modern Optics, Vol. 41, No. 7, 1994, pp. 1415-1426. doi:10.1080/09500349414551351
- J. Zhou, J. Peatross, M. M. Murnane, H. C. Kapteyn and I. P. Christov, “Enhanced High-Harmonic Generation Using 25 fs Laser Pulses,” Physical Review Letters, Vol. 76, No. 5, 1996, pp. 752-755. doi:10.1103/PhysRevLett.76.752
- M. Lein, “Mechanisms of Ultrahigh-Order Harmonic Generation,” Physical Review A, Vol. 72, No. 5, 2005, Article ID: 053816. doi:10.1103/PhysRevA.72.053816
- J. Tate, T. Auguste, H. G. Muller, P. Salières, P. Agostini and L. F. DiMauro, “Scaling of Wave-Packet Dynamics in an Intense Midinfrared Field,” Physical Review Letters, Vol. 98, No. 1, 2007, Article ID: 013901. doi:10.1103/PhysRevLett.98.013901
- K. Schiessl, K. L. Ishikawa, E. Persson and J. Burgdörfer, “Quantum Path Interference in the Wavelength Dependence of High-Harmonic Generation,” Physical Review Letters, Vol. 99, No 25, 2007, Article ID: 253903. doi:10.1103/PhysRevLett.99.253903
- D. Cricchio, P. P. Corso, E. Fiordilino, G. Orlando and F. Persico, “A Paradigm of Fullerene,” Journal of Physics B, Vol. 42, No. 8, 2009, Article ID: 085404. doi:10.1088/0953-4075/42/8/085404
- D. Cricchio, E. Fiordilino and F. Persico, “Electrons on a Spherical Surface: Physical Properties and Hollow Spherical Clusters,” Physical Review A, Vol. 86, No. 1, 2012, Article ID: 013201. doi:10.1103/PhysRevA.86.013201
- N. Moiseyev and M. Lein, “Non-Hermitian Quantum Mechanics for High-Order Harmonic Generation Spectra,” Journal of Phycial Chemistry A, Vol. 107, No. 37, 2003, pp. 7181-7188. doi:10.1021/jp034390y
- Z.-Y. Zhou and J.-M. Yuan, “Strengthened Hyper-Raman Lines with the Coherent Superposition State,” Chinese Physics Letters, Vol. 24, No. 3, 2007, pp. 683-686. doi:10.1088/0256-307X/24/3/026
- T. Millack and A. Maquet, “Hyper-Raman Lines Produced During High Harmonic Generation,” Journal of Modern Optics, Vol. 40, No. 11, 1993, pp. 2161-2171. doi:10.1080/09500349314552191
- F. I. Gauthey, C. H. Keitel, P. L. Knight and A. Maquet, “Role of Initial Coherence in the Generation of Harmonics and Sidebands from a Strongly Driven Two-Level Atom,” Physical Review A, Vol. 52, No. 1, 1995, pp. 525- 540. doi:10.1103/PhysRevA.52.525
- W. Chu, Y. Xie, S. Duan, N. Yang, W. Zhang, J.-L. Zhu, and X.-G. Zhao, “Model of Generating either Odd or Even Optical Harmonics by Varying the Coupling Parameters Between Source Quantum Dots,” Physical Review B, Vol. 82, No. 12, 2010, Article ID: 125301. doi:10.1103/PhysRevB.82.125301
- Z.-Y. Zhou and J.-M. Yuan, “Fine Structures of the Harmonic and Hyper-Raman Spectrum of the Hydrogen Atom in an Intense High-Frequency Laser Pulse,” Physical Review A, Vol. 77, No. 6, 2008, Article ID: 063411. doi:10.1103/PhysRevA.77.063411
- V. Kapoor and D. Bauer, “Floquet Analysis of Real-Time Wave Functions without Solving the Floquet Equation,” Physical Review A, Vol. 85, No. 2, 2012, Article ID: 023407. doi:10.1103/PhysRevA.85.023407
- A. Di Piazza and E. Fiordilino, “Why Hyper-Raman Lines Are Absent in High-Order Harmonic Generation,” Physical Review A, Vol. 64, No. 1, 2001, Article ID: 013802. doi:10.1103/PhysRevA.64.013802
- A. D. Bandrauk, S. Chelkowski and H. S. Nguyen, “Nonlinear Photon Processes in Molecules at High Intensities-Route to XUV—Attosecond Pulse Generation,” Journal of Molecular Structure, Vol. 735-736, No. 2, 2005, pp. 203-209. doi:10.1016/j.molstruc.2004.09.034

