Optics and Photonics Journal
Vol.3 No.6A(2013), Article ID:38495,4 pages DOI:10.4236/opj.2013.36A001
Optical Spectra and Stokes Shift in Nanometric Quantum Wells
1Departamento de Ciências Exatas, Universidade Federal de Lavras, Lavras, Brazil
2Condensed Matter Physics Department, “Gleb Wataghin” Physics Institute, University of Campinas—UNICAMP, Campinas, Brazil
Email: liermes@ifi.unicamp.br
Copyright © 2013 Antonio A. P. Silva et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received May 4, 2013; revised June 9, 2013; accepted July 11, 2013
Keywords: Heterostructures; Non-Conventional Statistical Mechanics; Stokes Shift
ABSTRACT
We consider semiconductor heterostructures in nanometric quantum wells, which as a consequence of the growth process display at the rugged interfaces fractal characteristics, and largely influence optical and transport properties of the carriers system. The photoluminescence and excited photoluminescence spectra in such fractal conditions are theoretically analyzed, obtaining good agreement with the experimental results. The Stokes shift and linewidth are strongly dependent on the nonequilibrium thermomechanical-statistical state of the system. The Stokes shift has its origin in the presence of a gain region in the absorption spectrum, only present when the carriers system is in a statistical degenerate state.
1. Introduction
A particular case of physical interest, related to the present day development of modern technologies, is the one of the semiconductor heterostructures with the presence of quantum wells (QW) with nanometric widths. The growing of heterostructures produce QW with fractalon-average interfaces [1], which greatly affect their optical, transport and other properties. It has been noticed [2] that there is general agreement that the so-called Stokes shift, i.e., the shift of the peak position of the emission spectrum (PL) below that of the photoluminescence excited spectrum (PLE), provides a “rough and ready” indicator of sample quality. The optical properties PL and PLE in complex-structured nanometric QW have been extensively studied and reported in References [3,4], where the experimental details and the observed PL and PLE spectra of four samples of GaInP/GaAs with quantum wells widths of 15, 30, 50, and 80 nanometers are presented, followed by the theoretical analysis. Here we further reconsider these experiments to perform a study for characterizing the observed Stokes shifts and linewidths, in the process determining their origins. On this, on a quite different line, the question has been considered, by Nang et al. [2]. Next we briefly describe the theoretical analysis of the PL and PLE spectra.
2. Theory and Method
On one side, the photoluminescence spectrum arising out the recombination of electron-hole pairs in a quantum well, occurring in conditions such that there exists a photo-injected plasma with mobile electrons and holes, and the non-degenerate limit is valid, is considered. The intensity of the photoluminescence is given by
 (1)
(1)
where, 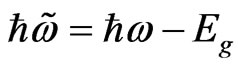 (Eg is the energy gap), the photon momentum has been neglected (then
(Eg is the energy gap), the photon momentum has been neglected (then  is the same for the electron and the hole), and C is a proportionality constant (containing the square modulus of the carrierradiation interactions which is taken as independent); e stands for electrons and h for holes. We can see that there is a sequence of bands corresponding to transitions between the different states characterized by n and
is the same for the electron and the hole), and C is a proportionality constant (containing the square modulus of the carrierradiation interactions which is taken as independent); e stands for electrons and h for holes. We can see that there is a sequence of bands corresponding to transitions between the different states characterized by n and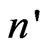 . Moreover, in Equation (1),
. Moreover, in Equation (1), 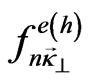 are the populations in states
are the populations in states  at any time t (the system is out-of-equilibrium and thus its macroscopic state evolves in time), in Boltzmann-Gibbs statistics given by Fermi-Dirac-like distributions at each time t. They depend on a nonequilibrium temperature and chemical potential evolving in time [5] and on the energy levels
at any time t (the system is out-of-equilibrium and thus its macroscopic state evolves in time), in Boltzmann-Gibbs statistics given by Fermi-Dirac-like distributions at each time t. They depend on a nonequilibrium temperature and chemical potential evolving in time [5] and on the energy levels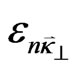 . The latter are energy levels (with an index n = 1, 2, … for the discrete levels and
. The latter are energy levels (with an index n = 1, 2, … for the discrete levels and  for the free movement in the x-y plane), whose textbook expression is
for the free movement in the x-y plane), whose textbook expression is
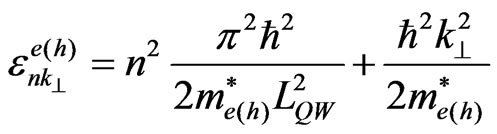 (2)
(2)
where, L is the quantum-well width and 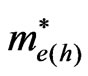 is the effective mass, which corresponds to the use of perfectly smooth bidimensional boundaries. But the roughness of the boundaries need be taken into account in these nanometric scale geometries, and thus the boundary conditions to be placed on the wave functions are space dependent.
is the effective mass, which corresponds to the use of perfectly smooth bidimensional boundaries. But the roughness of the boundaries need be taken into account in these nanometric scale geometries, and thus the boundary conditions to be placed on the wave functions are space dependent.
Hence, to deal with these types of systems, the researcher has to face difficulties with the theoretical analysis due to the constrained geometry that is present (where various phenomena develop in nanometer scales). Evidently, we do have here that the most relevant question to be dealt with is the one related to the interface microroughness, that is, a spatially varying confinement with subnanometer roughness in shape not much smaller than the well width, which leads to spatially correlated energies and wavefunction boundary conditions. As a conesquence the different physical properties of these systems appear as, say, “anomalous” when the results are compared with those that are observed in bulk materials. In the case of photoluminescence, which we consider here, the “anomaly” consists in that the position and shape of the spectrum differ from the one observed in bulk materials. Moreover, the spectrum changes with the width L of the quantum well, approaching to the “normal” one in bulk when QW is sufficiently large (typically hundreds to thousands of nanometers, and depending on the growth procedure too). Furthermore, for the case of a specific modeling using a computer simulation, Runge and Zimmermann [6] have obtained a detailed description of the expected spectra, and have determined the Stokes shift between absorption and luminescence, as well as the luminescence line widths, for different temperatures, evidencing (in this computer experiment) a behavior in good qualitative agreement with the one observed in experiments. This illustrates the fact that the “anomaly”, in the comparison with the case of a bulk sample, is a result of the influence of the ruggedness of the boundary surfaces, which strongly influences the determination of the quantum states which are to the used in place of those of Equation (2) in Equation (1). Consequently, the mechanical-statistical treatment via Boltzmann-Gibbs ensemble formalism has its application impaired because of the spatial correlations resulting from the spatially varying confinement (as noted above), which is an information one does not have access to (obviously the interface ruggedness varies from sample to sample and one does not have any easy possible means to satisfactorily determine the topography of the interfaces).
For circumventing the practical difficulty of applying the usual approach of the Gibbs ensemble formalism to these highly spatially correlated systems, a fact referred-to as a failure to satisfy Fisher’s Criterion of Sufficiency in statistics [7] (which in this case, we restate, consists in the failure to have access to the proper quantum levels of energy), the so-called Non-Standard Statistical Mechanics needs be introduced (see for example the feature article in the Reference [8]). This statistical approach appears to be quite appropriate for dealing with systems when there exist the “insufficiency” condition consisting in not being able to introduce in the calculation some kind of information which is relevant to the characterization of the physical property under analysis, the so-called “hidden constraints” problem.
For the present study, we resort to the use of the said Non-Conventional Statistical Mechanics (NCSM), [8] and among the existing many different approaches we choose the one of Renyi [9-11]. In the calculation of the photoluminescence spectrum of Equation (1), in the absence of information on the proper energy levels of carriers in the nanometric quantum well, we use the ideal energy levels of Equation (2) but, as said, in the framework of NCSM and resorting to Renyi’s approach, where, the populations  in Equation (1) take the form [8]:
in Equation (1) take the form [8]:
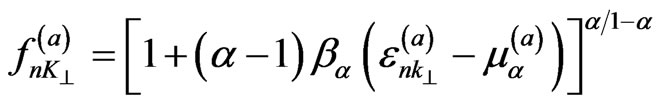 (3)
(3)
where the approximate sign means that contributions which are much smaller than those written here have been neglected; the terms in Equation (3) retains correlation effects between the single-particle states. Quantity 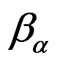 plays the role of the inverse of a nonequilibrium temperature,
plays the role of the inverse of a nonequilibrium temperature,  of quasi-chemical potentials, and α is Renyi’s adjustable parameter (usually called quasitemperature). It can be noticed that taking the limit of α going to 1, the distribution in Equation (3) acquires the form of a nonequilibrium Fermi-Dirac-like distribution, meaning that if a fortiori one finds α ≈ 1 the condition of sufficiency is satisfied, viz., the energy levels of Equation (2) are appropriate (which is true for the case of nearly planar interfaces, or, as we shall see, the case of wells with large widths, that is, order of magnitudes larger than the heights of the interface imperfections).
of quasi-chemical potentials, and α is Renyi’s adjustable parameter (usually called quasitemperature). It can be noticed that taking the limit of α going to 1, the distribution in Equation (3) acquires the form of a nonequilibrium Fermi-Dirac-like distribution, meaning that if a fortiori one finds α ≈ 1 the condition of sufficiency is satisfied, viz., the energy levels of Equation (2) are appropriate (which is true for the case of nearly planar interfaces, or, as we shall see, the case of wells with large widths, that is, order of magnitudes larger than the heights of the interface imperfections).
On the other hand, the excited photoluminescence spectrum (PLE) is given by,
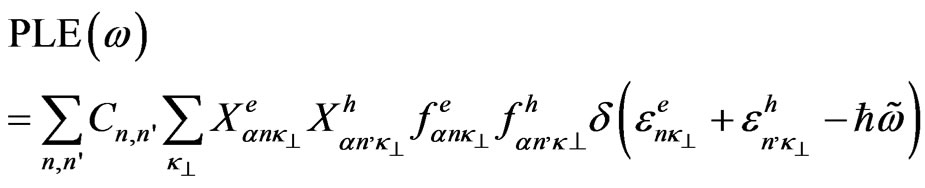 (4)
(4)
where, .
.
PLE is an experimental method that provides information on the absorption coefficient  [12], and we have that
[12], and we have that
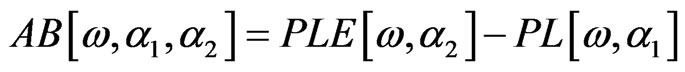 (5)
(5)
where it has introduced the important fact that, once the experimental protocols in the measurement of PL and PLE are different , according to the nonconventional statistics there should be used a different index αi (i with index 1 or 2) for each one [8].
3. Results and Discussion
Using the experimental results, the PL and PLE measurements for the four samples above mentioned, we show in the Figure 1 the corresponding absorption coefficients.
It can be noticed the important fact of the presence of a gain region in the spectrum (at low energies), becoming zero and going over an absorption region at the value of the energy that is equal to the quasi-chemical potential . This is indicative that the carrier system is in a statistical quantum degenerated state; if the conditions are such that it is a statistical nondegenerated state (quasi-chemical potential negative) no gain region is present. The existence of this region gives rise to the presence of the Stokes Shift and influences the linewidth.
. This is indicative that the carrier system is in a statistical quantum degenerated state; if the conditions are such that it is a statistical nondegenerated state (quasi-chemical potential negative) no gain region is present. The existence of this region gives rise to the presence of the Stokes Shift and influences the linewidth.
In the Figure 2 is displayed, for samples C15, C30 and C50, the theoretical calculation and experimental results of PL and PLE. In the lower right inset are indicated the values of the parameter alpha and the carrier’s quasi-temperature used. The case of the sample C80 has been omitted: at 80 nm the behavior is near normal (i.e., α near 1) and for such values the computing program fails.
In the Figures 1 and 2, is evident the crossover of both PL and PLE, which occurs at the energy of the quasi-
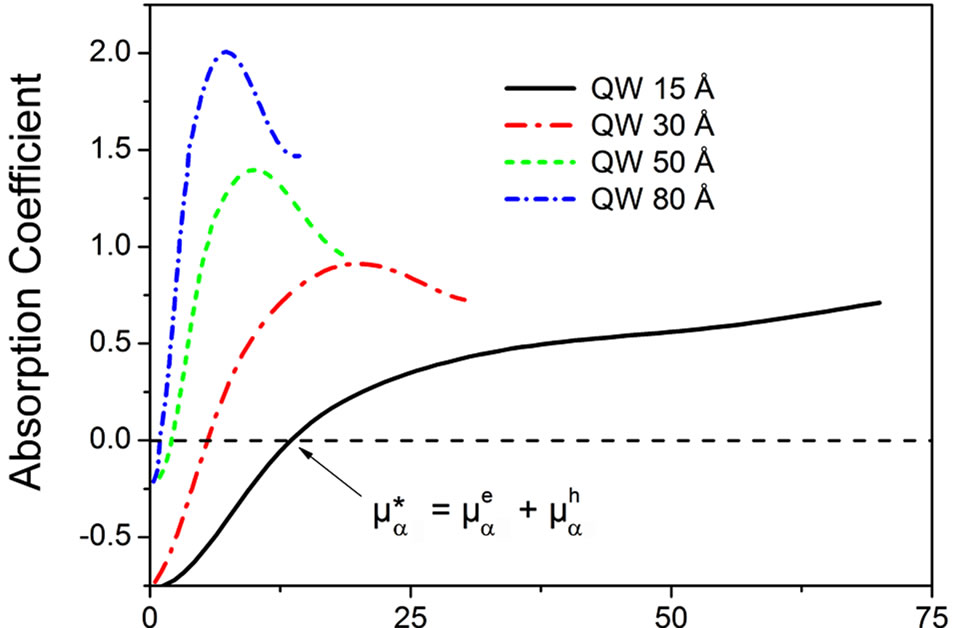
Figure 1. Absorption coefficient for the four samples in the experiment of the Ref. [3], showing the transition from gain to absorption.
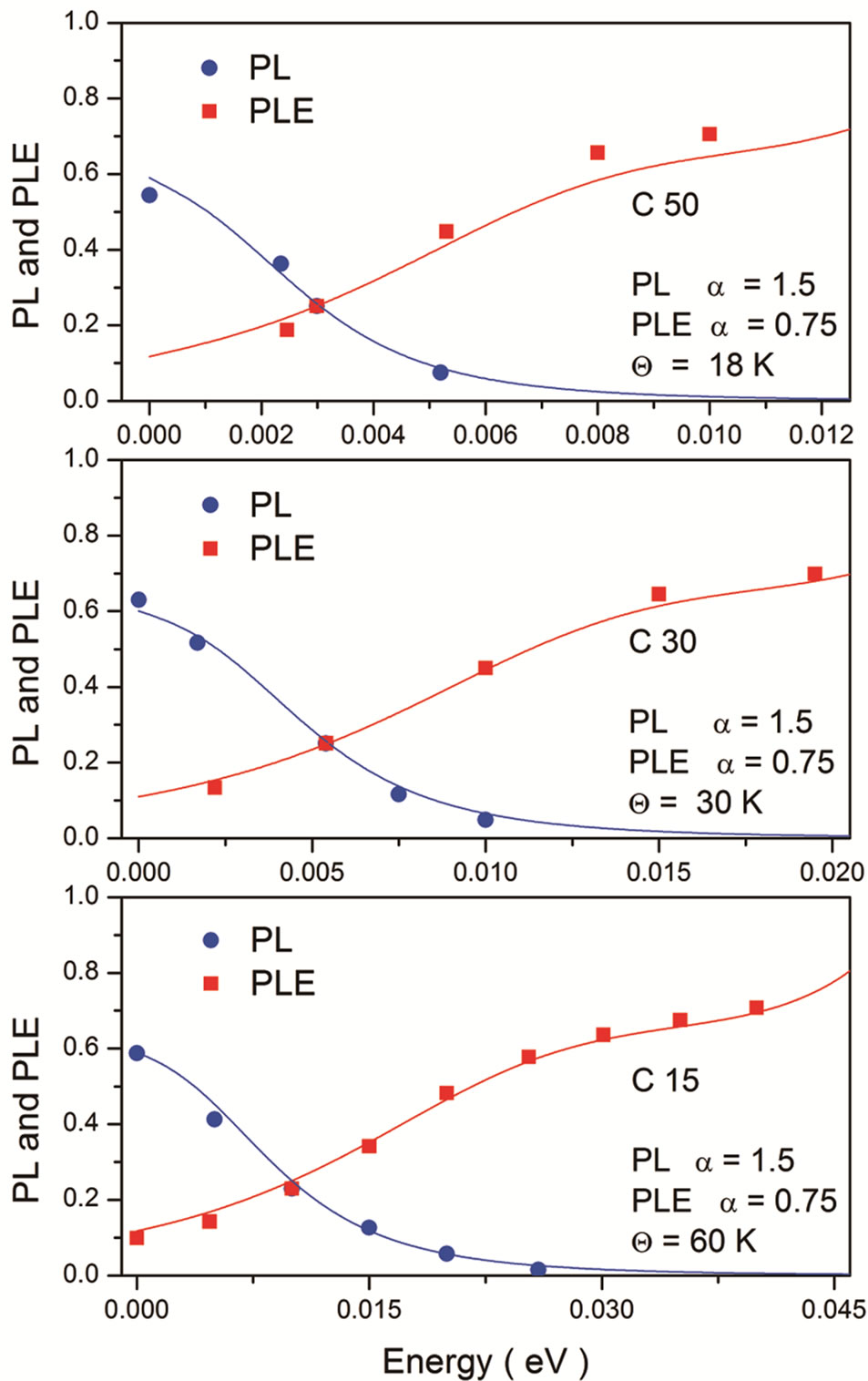
Figure 2. PL and PLE in three samples in the experiment of Ref. [3]: full line is the result of the theoretical calculation and square and dots are experimental data.
chemical potential, 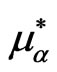 in each case (when in the absorption spectrum—cf. Equation (5)—there follows the change of the regime from gain to absorption).
in each case (when in the absorption spectrum—cf. Equation (5)—there follows the change of the regime from gain to absorption).
We present in Table 1 the values of the quasi-chemical potential 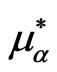 and the estimated values of the individual
and the estimated values of the individual 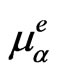 and
and .
.
In the Table 2 is shown the values of the Stokes Shift (SS) (experimental and from theory) and the full width at half maximum (FWHM).
In Figure 3 is shown the dependence of the Stokes Shift and of the line width with the quasi-chemical potential .
.
4. Conclusions
In summary, it has been presented a study of the optical properties of photoluminescence and excited photoluminescence in nanometric quantum wells in semiconductor heterostructures. Width of the QW and growth protocol largely influence on the characteristics of the spectra. We have considered in detail the study of the Stokes shift and of the linewidth which provide a “rough and ready” indication of the sample quality. These quantities are strongly dependent on the nonequilibrium thermodynamical state of the system. It has been determined that the origin of the Stokes shift resides in the presence of the gain region in the absorption spectrum, that is, only present when the carriers are in a mechanical-statistical degenerate state.
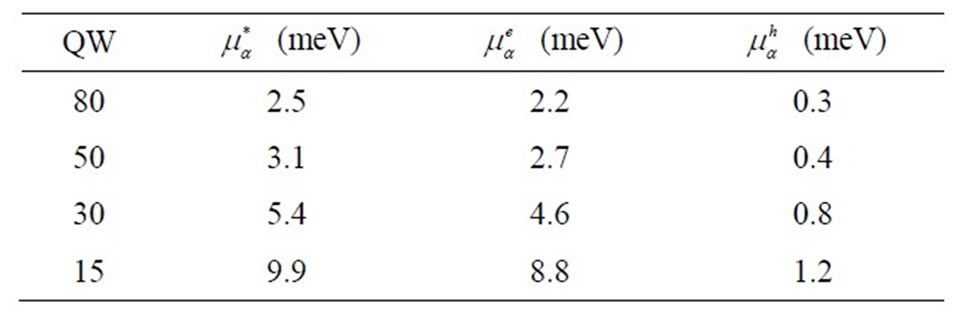
Table 1. Values of the quasi-chemical potential.
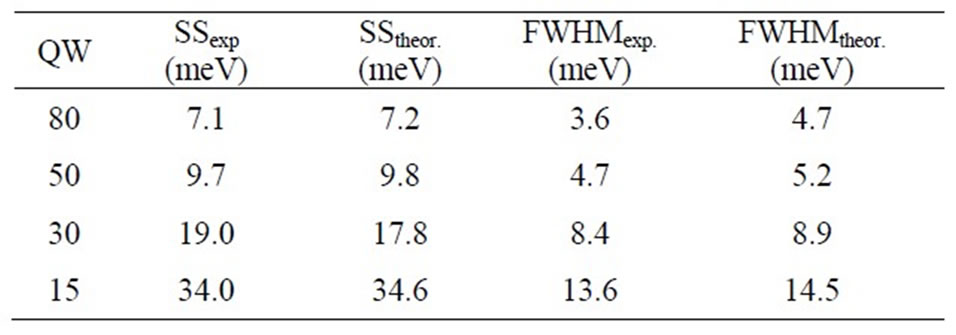
Table 2. Values of the stokes shift and FWHM.

Figure 3. Dependence of the stokes shift (full line) and of the FWHM (trace line) on values of the quasi-chemical potential.
5. Acknowledgements
We acknowledge financial support by the São Paulo State Research Agency (FAPESP).
REFERENCES
- A. F. Family and T. Viczek, “Dynamics of Fractal Surfaces,” World Scientific, Singapore, 1991.
- Fang Yang, M. Wilkinson, E. J. Austin and K. P. O’Donnell, “Origin of the Stokes Shift: A Geometrical Model of Exciton Spectra in 2D Semiconductors,” Physical Review Letters, Vol. 70, No. 3, 1993, pp. 323-326 (1993). http://dx.doi.org/10.1103/PhysRevLett.70.323
- E. Laureto, A. R. Vasconcellos, E. A. Meneses and R. Luzzi, “Characterization of Nanometric Quantum Wells in Semiconductor Heterostructures by Optical Spectroscopy,” International Journal of Modern Physics B, Vol. 18, No. 12, 2004, p. 1743. http://dx.doi.org/10.1142/S021797920402480X
- E. Laureto, “The Study on the Influence of the Interfaces in the Optical Properties of GaInP/GaAs Quantum Wells,” PhD Thesis, IFGW-UNICAMP, Campinas, 2002.
- A. Algarte, A. R. Vasconcellos and R. Luzzi, “Kinetics of Hot Elementary Excitations in Photoexcited Polar Semiconductors,” Solid State Physics, Vol. 173, No. 2, 1962, pp. 487-514. http://dx.doi.org/10.1002/pssb.2221730202
- E. Runge and R. Zimmermann, Adv. Solid. State Phys. Vol. 38, 1999, pp. 261-263.
- R. Fisher, “On the Mathematical Foundations of Theoretical Statistics,” Philosophical Transactions of the Royal Society A, Vol. 222, 1922, pp. 309-368. http://dx.doi.org/10.1098/rsta.1922.0009
- R. Luzzi, A. R. Vasconcellos and J. G. Ramos, “Revista del Nuovo Cimento,” Vol. 30, No. 3, 1999, pp, 98-157.
- A. Renyi, “On Measures of Entropy and Information,” 4th Berkeley Symposium on Mathematical Statistics and Probability, Vol. 1, Berkeley, 20 June-30 July 1961, pp. 547-561.
- A Renyi, “Probability Theory,” North Holland, Amsterdam, 1970.
- P. Jizba and T. Arimitzu, “The World According to Renyi,” Annals of Physics, Vol. 312, 2004, p. 17.
- P. Y. Yu and M. Cardona, “Fundamentals of Semiconductors,” Springer, Berlin, 2001.
NOTES
*Deceased, October 13, 2012.

